一類Bogdanov-Takens系統在分段多項式擾動下極限環個數的估計

晏兵川，李寶毅，張永康

（天津師范大學數學科學學院，天津300387）

1 引言和主要結果

弱化Hilbert第16問題一直是常微分方程定性理論的熱門課題之一[1-2].Bogdanov-Takens系統（B-T系統）是向量場的分岔理論研究中一類重要的近Hamilton系統.文獻[3-10]研究了在二、三、四次多項式擾動下B-T系統的極限環個數.令Mk（h）為擾動系統的k階Melnikov函數.對于B-T系統的n次多項式擾動，文獻[11]證明了當M1（h）?0時，極限環個數的上確界為n-1（計重數）;文獻[12]證明了當M1（h）≡0，M2（h）?0時，極限環個數的上確界為（計重數）;文獻[13]證明了當Mi（h）≡0（i=1，2，…，k-1），Mk（h）?0時（k≥3），極限環的個數不超過k（n-1）-1（計重數）.

隨著分岔理論的發展，一些研究開始關注分段光滑向量場的定性分析.文獻[14]將平面分為上下2個區域，證明了在分段n次多項式擾動下B-T系統的極限環個數不超過12n+6（計重數）.文獻[15]將平面分為左右2個區域，證明了在非連續（連續）分段n次多項式擾動下B-T系統的極限環個數不超過16n+計重數）.文獻[16]證明了將平面等分成3個扇形區域時，一類分段線性Hamilton系統在n次多項式擾動下至少可以產生2n+（計重數）個極限環.文獻[17]證明了一類平面拋物-橢圓型分段光滑線性Hamilton系統在n次多項式擾動下極限環的個數不超過（計重數）.

本文將平面分為上下2個區域，通過計算一階Melnikov函數，估計非連續分段n次多項式擾動的B-T系統

的極限環個數，其中：0<ε?1，n∈N+，

當ε=0時，未擾動系統（1）0的Hamilton函數為

設Γh與x軸正半軸和負半軸分別交于點Bh（b（h），0）和Ah（a（h），0）.

本文的主要結果為：

定理 在非連續分段n次多項式擾動下，當h∈一階Melnikov函數M（1h）?0時，擾動系統（1）ε的極限環個數不超過

2 一階Melnikov函數

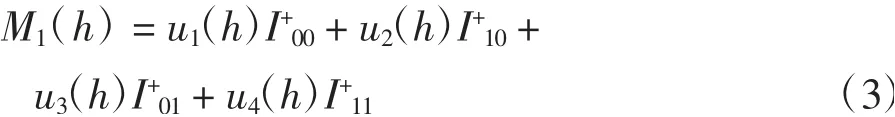
其中：u1（h）、u2（h）、u3（h）、u4（h）為h的多項式，且

證明 由Γh關于x軸的對稱性可得

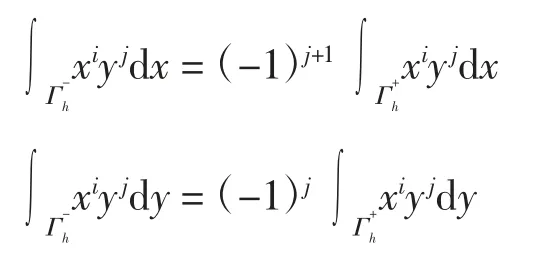
因此

則有

下面只需證明對i+j=n，I+ij滿足

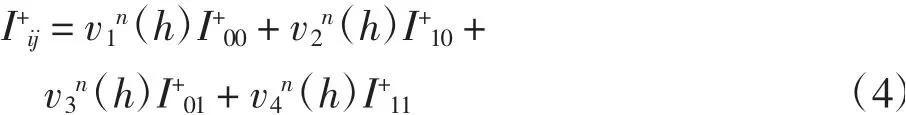
其中：v1n（h）、v2n（h）、v3n（h）、v4n（h）為h的多項式，且

對式（2）關于x求導得

式（5）兩端同乘以xi-2y jdx（i≥2），并沿Γ+h積分得

當i=2時，有

即

當i≥3時，由式（6）可得

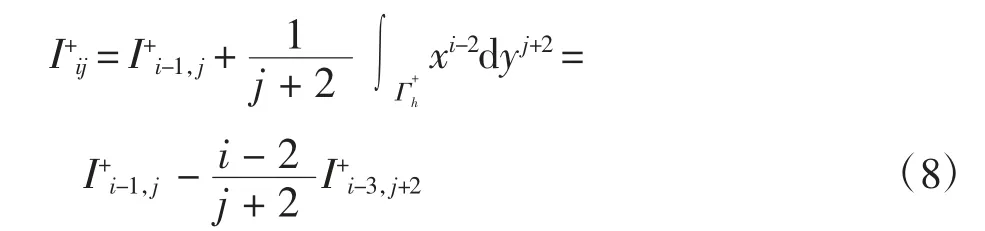
式（2）兩端同乘以xiy j-2dx（j≥2），并沿Γ+h積分得

即

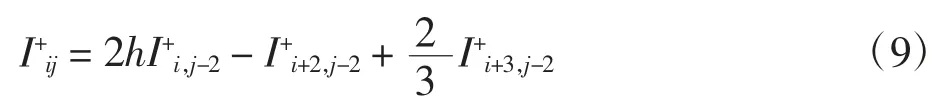
由式（8）～式（9）可得

在式（7）和式（10）中分別取j=0和（i，j）=（0，2），可得

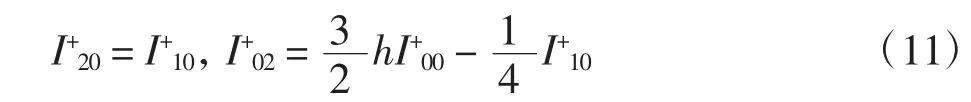
在式（8）和式（7）中分別取（i，j）=（3，0）和j=1，可得

在式（10）中取（i，j）=（1，2）、（0，3），可得

下面對n使用數學歸納法證明式（4）成立.由式（11）～式（13）可知式（4）對n=0、1、2、3成立.假設當n=i+j≤k-1（k≥4）時式（4）成立，則當n=k，即i+j=k時，在式（10）中取（i，j）=（0，k）、（1，k-1），在式（7）中取j=k-2，在式（8）中取（i，j）=（l，k-l）（3≤l≤k），可得

由歸納假設，當n=k時，I+ij有形如式（4）的表達式.下面利用式（14）估計多項式v1n（h）、v2n（h）、v3n（h）、v4n（h）的次數.

情形1 當（i，j）=（0，k）、（1，k-1）時，有

因此可得

情形2 當（i，j）=（2，k-2）時，I+2，k-2=I+1，k-2，此時顯然有

情形3 當（i，j）=（l，k-l）（3≤l≤k）時，有

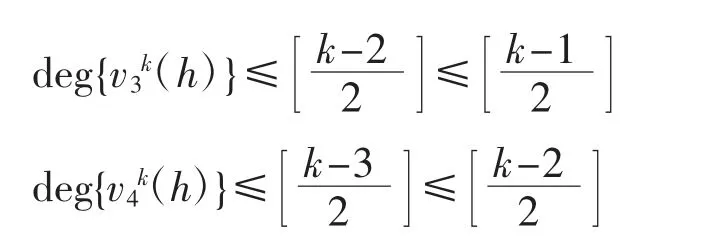
綜上可得式（4）成立.引理1證畢.

引理2I+00、I+′00在上無零點.

證明 將Ah（a（h），0）和Bh（b（h），0）代入式（2）得

則有

因為a（h）≠b（h）且a（h）+b（h）<1，故I+′00≠0.引理2證畢.

記Δ（h）=h（6h-1）.

引理3I+00、I+10滿足Picard-Fuchs方程組

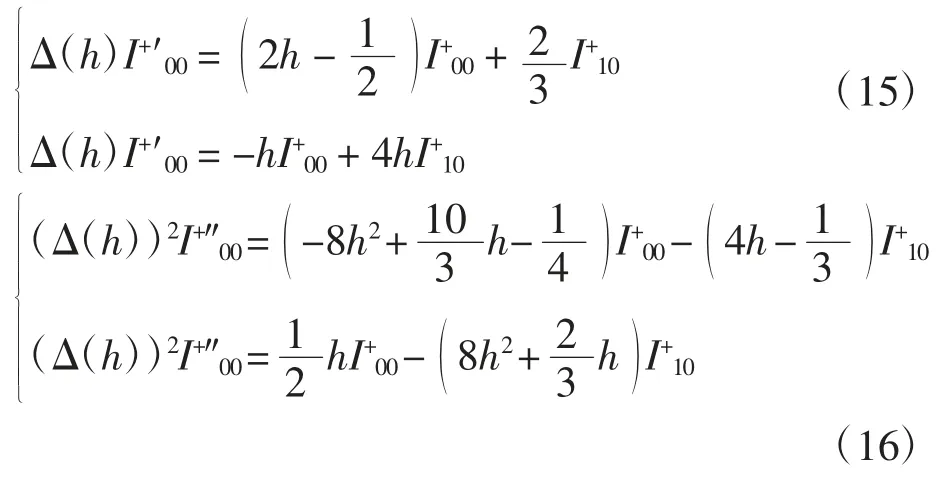
證明 考慮積分

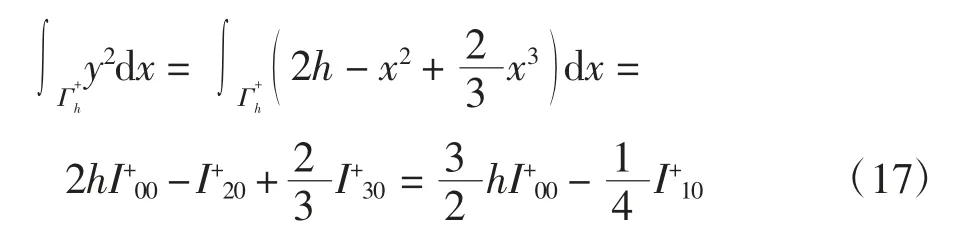
注意到

因此對式（17）關于h求導可得

整理得

考慮積分

注意到

因此，對式（19）關于h求導可得

整理得

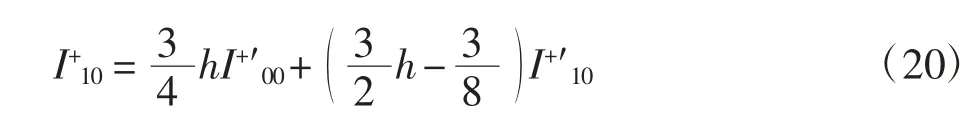
聯立式（18）和式（20）可得

因此式（15）成立.對式（15）關于h求導，經整理可得式（16）.引理3證畢.

利用

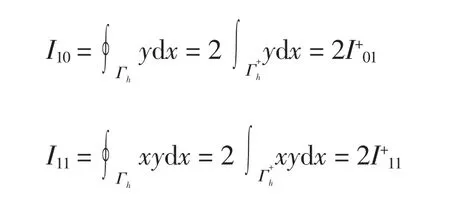
并結合文獻[18]的推論1*可得引理4.

引理4I+01、I+11滿足Picard-Fuchs方程組

3 極限環個數的估計

命題1[19]設系統滿足

（1）P（h）在閉區間[a，b]上連續，在開區間（a，b）內可導；

（2）A（h）和B（h）在閉區間[a，b]上連續，F（h，P）在[a，b]×[mp，Mp]上連續，其中[mp，Mp]為F（h，P）在[a，b]上的值域.

則有以下結論：若A（h）和B（h）在開區間（a，b）內分別有個和個零點（，計重數），則函數P（h）在開區間（a，b）內至多有個零點（計重數）.

命題2[15]P2（h）、P1（h）、P0（h）和R（h）為開區間K上的充分光滑的連續函數，P2（h）的零點是孤立的，且

存在非平凡解Φ1（h），則

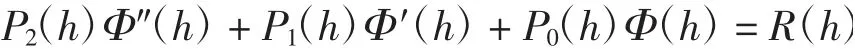
的任一解在K上的零點個數（計重數）不超過p+2w+r+2，其中p、w、r分別為P2（h）、Φ1（h）、R（h）在K上的零點個數（計重數）.

定理的證明 （f h）在上的孤立零點個數記為#f（h）（計重數）.

當n=1時，系統（1）ε的一階Melnikov函數為

其中：u1、u2、u3為常數.令φ1（h）=I+01，定義二階微分算子（其中I為恒同算子），由式（22）可知L1（φ1（h））≡0，將式（18）和式（20）代入式（16）可得

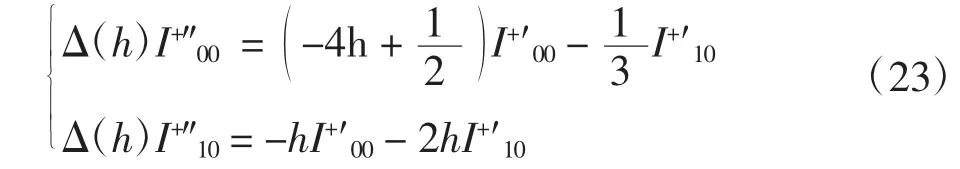
則有

其中：

由式（23）可得

令G（h）=α11（h）+α12（h）w（h），則有

其中：

所以#B1（h）≤3，由命題1可知

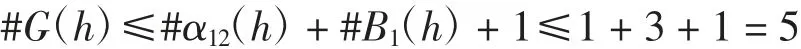
再由命題2可得

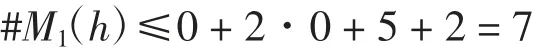
即當M1（h）?0時，系統（1）ε至多存在7個極限環.

當n≥2時，在式（3）中令

對ψ2（h）關于h求導，由引理4可得

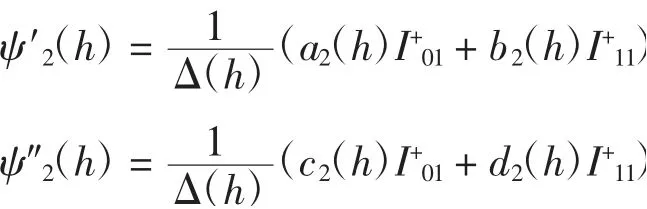
其中：

從而

事實上，設P1（h）為k次多項式，P2（h）和P0（h）均為k+1次多項式，則式（24）左端為關于h的次數不超過β+k+1的多項式，共有β+k+2項，令其各項系數為0，得到β+k+2個線性方程.式（25）左端為關于h的次數不超過α+k的多項式，共有α+k+1項，令其各項系數為0，得到α+k+1個線性方程.因此可得到一個含有α+β+2k+3個方程的線性方程組.

又由于P1（h）中有k+1個待定系數，P2（h）和P0（h）中分別有k+2個待定系數，則線性方程組共有3k+5個待定系數，因此當3k+5>α+β+2k+3，即k>α+β-2時，線性方程組存在非零解.取k=α+β-1，則存在系數不全為0的實系數α+β-1次多項式P1（h），α+β次多項式P2（h）和P0（h），使得L（ψ2（h））≡0.

對ψ1（h）關于h求導，結合式（18）、式（20）和式（23）可得

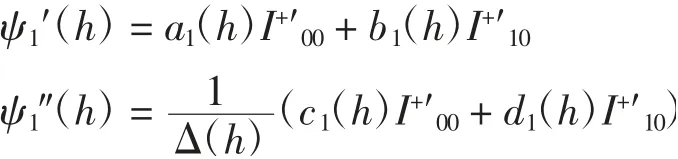
其中：

從而

因此

其中：

從而

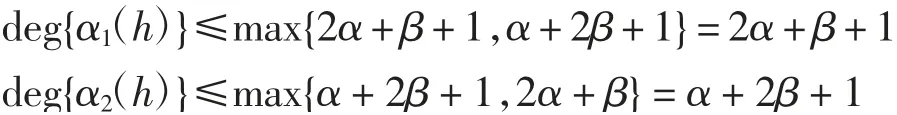
令G（h）=α1（h）+α2（h）w（h），則有

其中：

則有

因此，由命題1可知

由P2（h）的多項式次數可得

根據Petrov定理[20]可知w=#ψ2（h）≤α+β，再由命題2可得

取n=1，有因此當M（1h）?0時，擾動系統（1）ε的極限環個數不超過計重數）.定理證畢.