改進BFO優化BPNN的自來水混凝加藥預測

張長勝,韓 濤*,錢 斌,胡 蓉,田海湧,毛 輝,王 卓

改進BFO優化BPNN的自來水混凝加藥預測

張長勝1,韓 濤1*,錢 斌1,胡 蓉1,田海湧2,毛 輝3,王 卓1

(1.昆明理工大學信息工程與自動化學院,云南 昆明 650500；2.云南樹業科技有限公司,云南 昆明 650032；3.中國市政工程華北設計研究總院有限公司昆明分公司,云南 昆明 650051)

本文給出一種量子粒子群 (QPSO)算法、改進菌群覓食(IBFO)算法優化反向傳播神經網絡(BPNN)的混凝投藥預測模型,利用量子粒子群的個體極值與群體極值更新細菌覓食算法趨化過程中細菌位置;通過細菌協同改進趨化算子提高優化精度,結合差分算法改進繁殖算子解決部分維度退化問題,加入輪盤賭方法作為選擇機制改進遷移算子來克服優化過程中優秀解消失的缺陷;進而優化BP神經網絡的權值、閾值以此預測混凝劑投藥量.對云南某自來水廠的數據進行離線訓練和模型測試,結果表明,所提算法預測結果的均方誤差(MSE)達0.0116mg/L,平均絕對誤差百分比(MAPE)達1.36%,在預測精度和穩定性上優于BFO-BPNN、PSO-BPNN等模型.

混凝加藥；預測模型；BPNN；BFO；QPSO

自來水廠水處理流程包括凝聚、混凝、沉淀、消毒及過濾5個階段,混凝效果直接影響后續處理設備生產負擔及成本,精準投藥對其具有決定性作用.故混凝投藥量閉環控制是自來水廠生產工藝的核心,也是水處理專家和研究學者急需解決的問題.自來水廠水處理混凝投藥過程存在非線性、多干擾等問題,并且我國地域遼闊、氣候復雜多樣、局部地區存在旱雨季,提高生產過程中抗干擾能力、保證出廠水質,對其穩定生產意義深遠.

近年,將自抗擾控制器與Smith預估器相結合的智能算法[1]、數據驅動控制[2]等彌補了加藥輸出信息滯后的缺點,但抗突變干擾能力較弱鑒于此,有學者提出通過對源水典型水質參數的檢測,利用神經網絡[3-4]的容錯性、自學習性和自適應能力,建立混凝投藥系統投藥量預測模型.于是Chan等[5]研究基于均值聚類和自適應神經模糊推理的混合算法,利用來自Bansong WTP的數據來預測沉降水的濁度和最佳混凝劑用量,對雨季的混凝預測作出了補充.徐少川等[6]引入CMAC改進自學習算法構建混凝投藥控制器,在穩定保證出廠水質的同時,降低凈水生產成本.饒小康[7]采用Elman神經網絡算法對獲取的歷史數據預處理后進行訓練和自適應學習,構建了用于混凝投藥的凈水控制器.與神經模糊控制、CMAC神經網絡、Elman神經網絡相比[5-8],BP神經網絡在非線性映射、自學習和自適應、容錯等方面具有獨特的優勢.

但BP神經網絡也存在過擬合[9]和泛化能力較弱[10]的問題.遺傳算法(GA)與粒子群算法(PSO)具有良好的全局搜索能力,可以快速地將解空間中的全體解搜索出.國內學者[11]研究GA-BP網絡結構的投藥量預測模型,實現混凝劑的實時最佳投加.魏津瑜等[12]將PSO與BP相結合,使得預測精度明顯提高.

與GA、PSO相比,菌群覓食(BFO)[13]算法收斂速度更快、且更易于跳出局部極小值.因此,本文以云南某自來水廠的混凝投藥為研究對象,將量子粒子群(QPSO)算法與改進型菌群覓IBFO)算法相結合來優化BP神經網絡混凝投藥預測模型.通過對比不同優化算法在標準函數下的全局最優值,以及對比不同優化算法下BP神經網絡的損失值、預測投藥量和預測投藥量誤差,綜合評估各算法性能,旨在為水廠混凝投藥環節提供參考.

1 模型方法

1.1 量子粒子群

QPSO算法以狄拉克(DELTA)趨阱為基礎,認為每個粒子具有量子行為,即不能同時確定位置和速度的精確值[14-15],因此具有量子行為的粒子在移動時并沒有確定的軌跡,可以在全部可行解空間中進行搜素,以便得到全局最優解,故QPSO比標準PSO算法具有更優的全局搜索能力.其動力學原理如圖1所示.

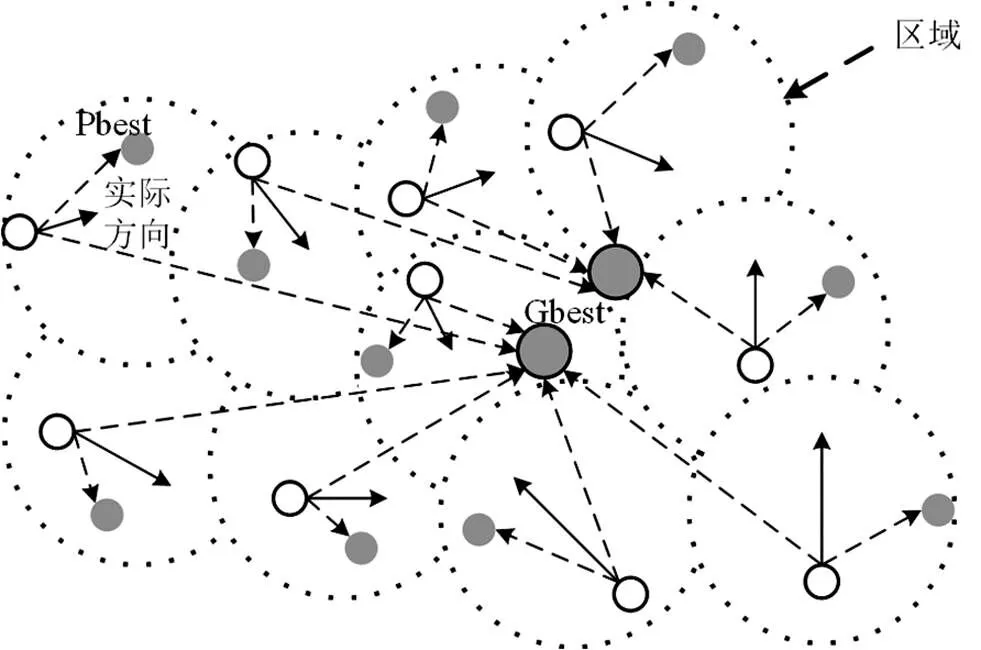
圖1 QPSO算法示意

粒子更新迭代方程為[16]:

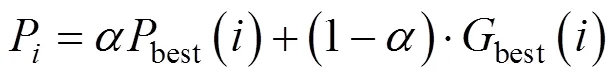
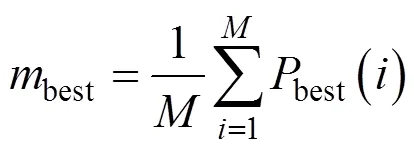
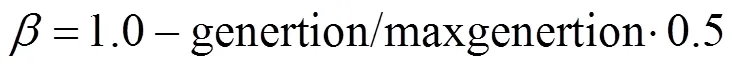
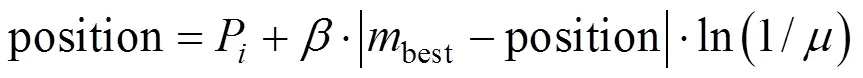
式中:是粒子群種群數量;best是個體極值best的平均值;best是粒子群群體極值;generation為當前進化代數;max generation為設定的最大進化代數;為[0,1]之間的隨機數;為收縮擴張系數.

1.2 菌群覓食算法

1.2.1 傳統細菌覓食優化算法BFO算法基于大腸桿菌的搜索和最佳覓食決策能力,細菌坐標代表了優化問題的單個解決方案,根據覓食群體的動態,這些試驗解決方案集合趨向于最優解決方案細菌種群.

初始細菌位置,每一個細菌代表待求解函數的一個解,即:

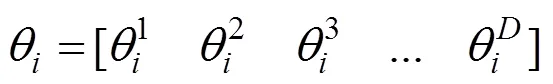
適應度函數選擇如公式(6):

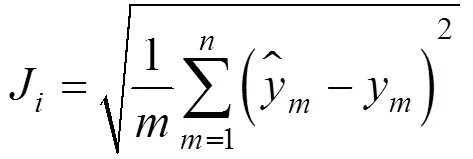
如圖2所示,細菌覓食系統3種主要機制為趨化、繁殖和遷移.趨化模擬了大腸桿菌細胞通過鞭毛泳動和翻轉的過程,在細菌生命周期內,可以沿著相同的方向游泳一段時間,當朝著喜歡的營養梯度地方移動并且避免進入有害的環境時,就需要進行順、逆時針翻轉改變方向,它根據環境變化交替這兩種模式.繁殖是在一定數量的完全游泳后,最不健康的細菌最終死亡,而每一個更健康的細菌(產生更高健康值的細菌)無性分裂成兩種放置在同一位置的細菌,以保持種群大小不變.遷移是為了逃避局部最優而進行的消除分散事件,即一些細菌小概率地被隨機清算,新的替換細菌被初始化在搜索空間的隨機位置.細菌間吸引和排斥的蜂擁模式有負面影響,排斥作用在趨化階段降低了優化的精度,且趨化階段還存在著部分維度的退化問題以及尋優過程中優秀解消失問題[17-18].

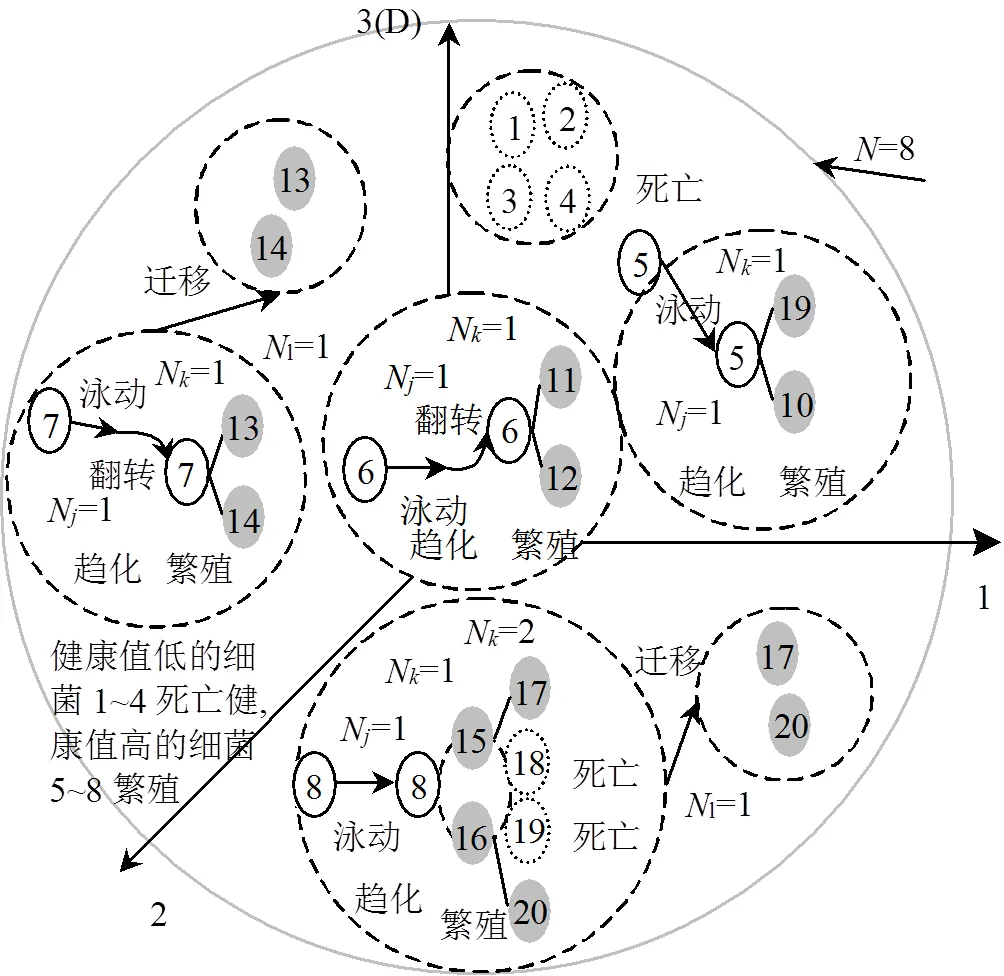
圖2 細菌覓食算法示意

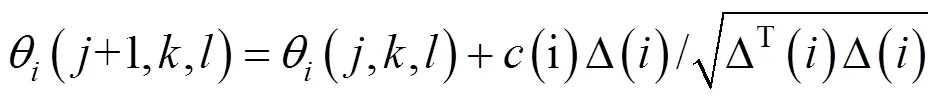
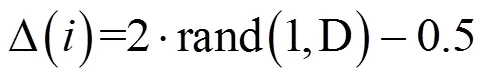
細菌翻轉行為的隨機性導致尋優速度過慢,且不能分享其它細菌在運動過程中的知識與經驗特點[19],故引入細菌向個體與種群學習的思想,使得其能夠記憶群體的適應度最優值與最優位置.在翻轉過程適應度變差時,則向群體最優學習,并克服隨機轉向變差的不足,從而進行位置更新.改進算法流程如圖3所示:

(2)繁殖算子改進經過N次趨化后,對第個細菌的健康值可累加為:

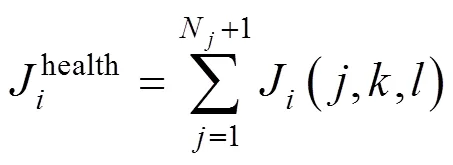
針對趨化過程中不是所有的維度都在進化、而部分維度退化現象,導致細菌可能出現局部最優狀況的問題,在繁殖環節引入差分算法,通過變異、交叉、選擇3個算子來尋優.

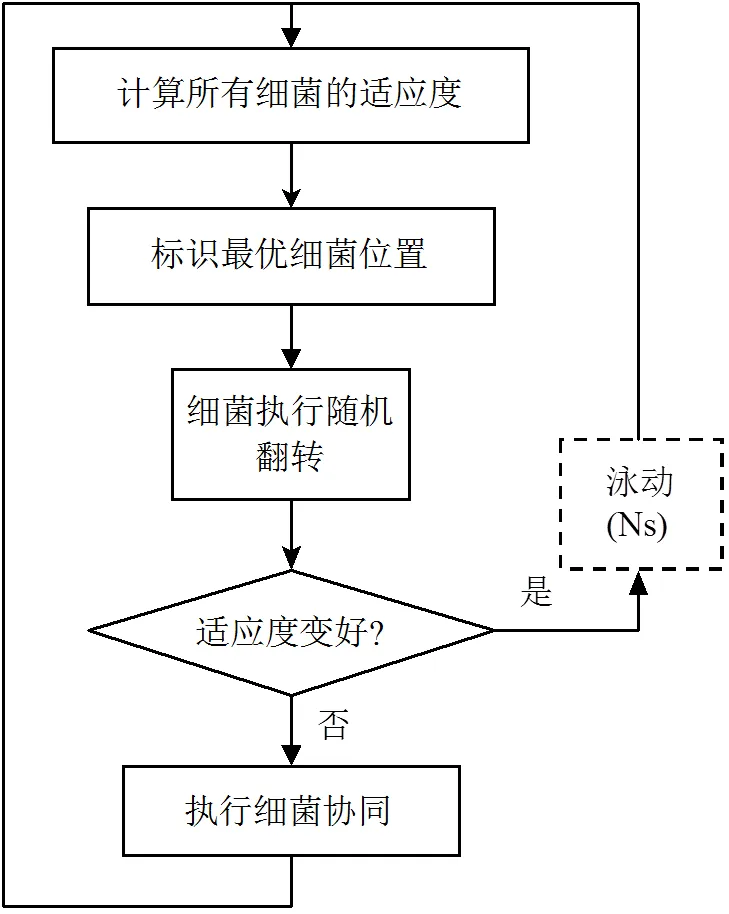
圖3 細菌協同

變異算子通過考慮種群內個體信息、縮放因子來拓展搜索空間,定義為:

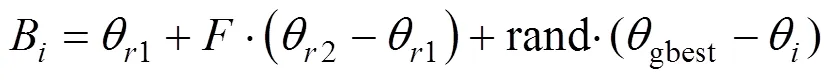
交叉算子定義為:

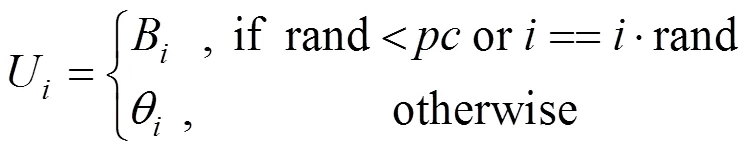
選擇操作為貪婪策略,即只有當產生的子代個體優于父代個體時才被保留,否則父代個體會被保留至下一代.

(3)遷移算子改進根據健康狀況及遷移概率Ped的設定值,將細菌消除并遷移到優化域中的隨機位置,可避免細菌陷入局部最佳狀態.但固定的Ped值會導致尋優過程中優秀解消失,影響算法的全局尋優能力,故結合輪盤賭方法優化遷移概率的選擇機制:

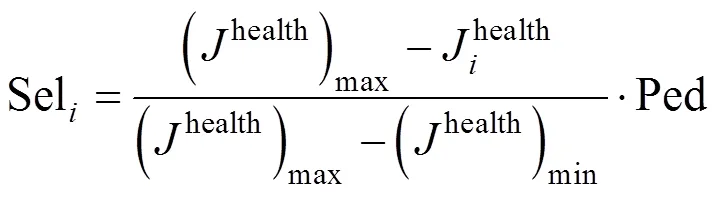
1.2.3 基于QPSO優化的細菌覓食算法 BFO算法具有較強全局優化能力,但可能會過早收斂導致全局解延遲[20-23].QPSO算法尋優速度較快,但可能出現局部最優解.為了克服二者缺點,利用QPSO算法優化BFO中的細菌初始位置,可進一步提高前者性能.QPSO-IBFO算法偽代碼如下:

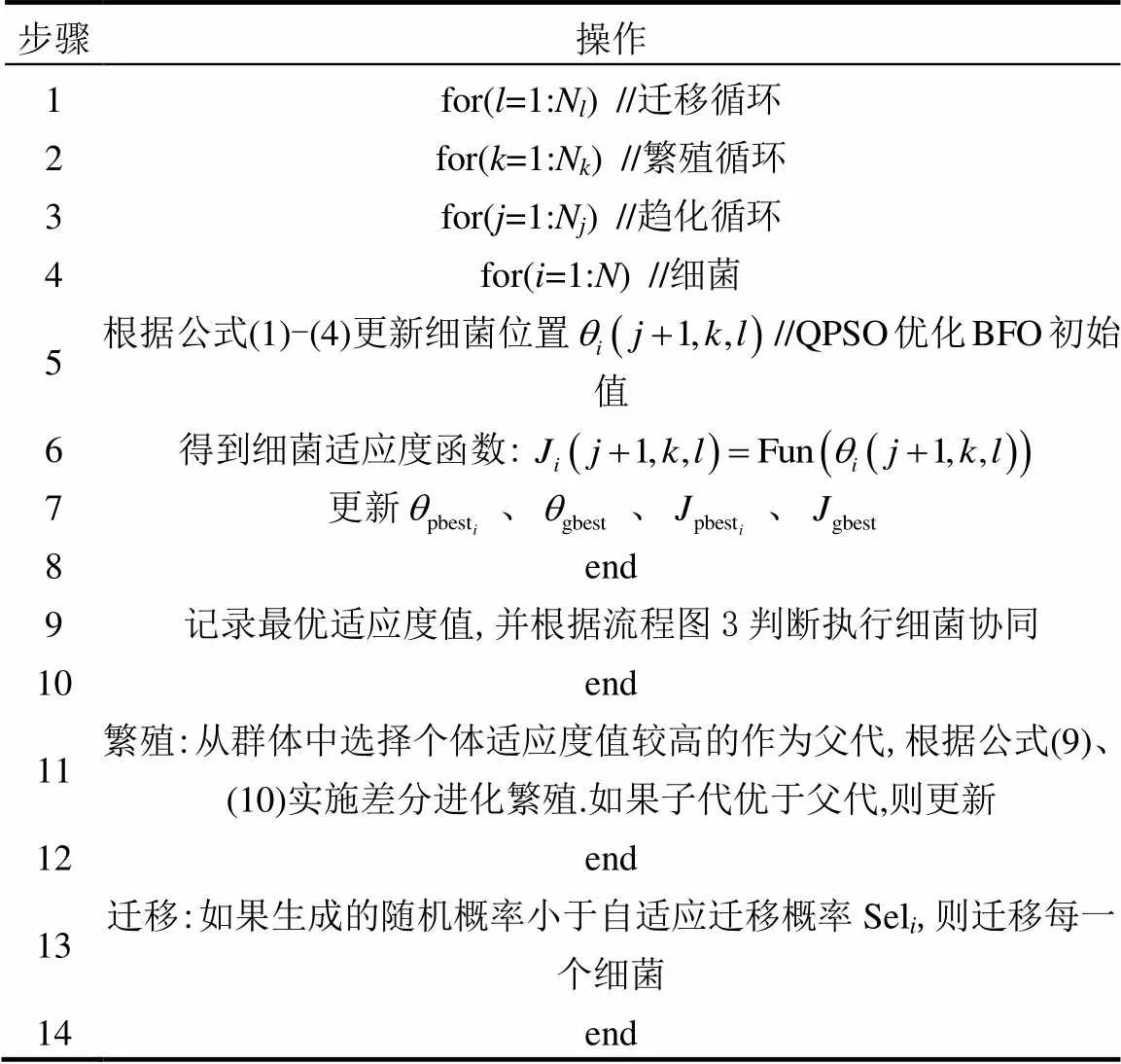
表1 QPSO-IBFO算法偽代碼

2 仿真及結果分析

2.1 QPSO-IBFO與各優化算法性能比較

為了準確測試算法性能,使用相同的隨機種子初始化方法,令BFO、PSO-BFO、QPSO-BFO算法中吸引劑數量、吸引劑釋放速度、排斥劑數量、排斥劑釋放速度及適應度增量因子為:d_attract = v_attract=d_repellant =v_repellant= 0.05,Jf = 0.5,其余參數設置如表2:

表2 優化算法參數

表3 標準測試函數

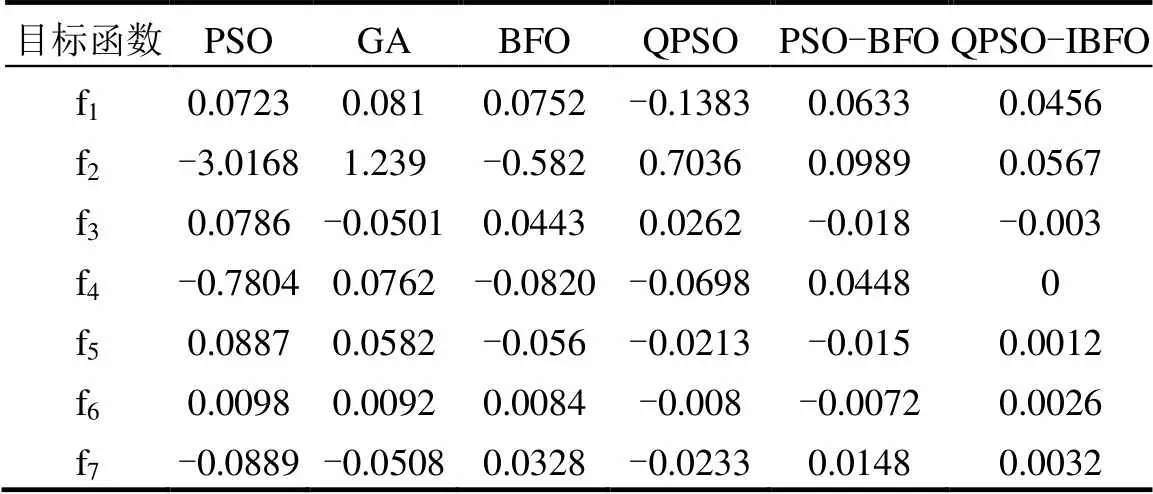
表4 不同優化算法迭代30次對應的f1- f7全局最優值

用表3中7個標準測試函數[24]來評估QPSO- IBFO算法的優化性能.

QPSO-IBFO與PSO、GA、BFO、QPSO、PSO-BFO等6種算法在測試函數下評價指標如表4所示:

顯然,QPSO-IBFO優化算法的尋優性能優于其它常規算法.

2.2 QPSO-IBFO-BPNN與各預測模型性能比較

以云南施甸某自來水廠為例,源水為水庫中上層低濁度水,每小時以勻速投5%濃度聚合氯化鋁(PAC)[25]溶液作為混凝劑.把原水濁度(NTU)、pH值、溫度(℃)、原水流量(m3/h)、出水濁度(NTU)作為影響因子,通過圖4所示基于QPSO-IBFO算法優化BP神經網絡的投藥控制器來預測混凝劑劑量(mg/L).根據水廠SCADA系統采集的1020組數據(750組為訓練集,250組為測試集,20組為驗證集),對投藥預測模型進行訓練、測試及驗證.

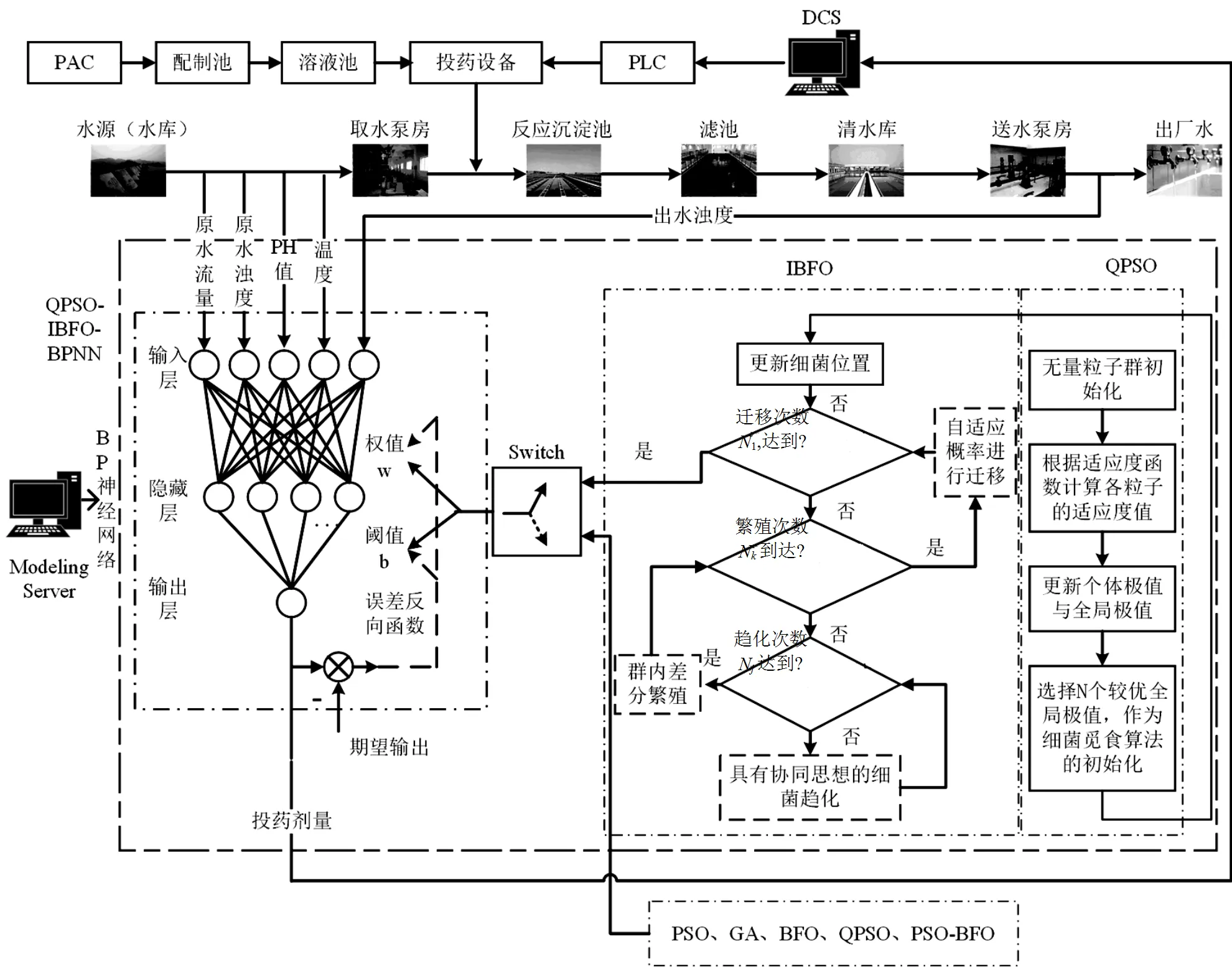
圖4 群智能算法優化BP神經網絡的投藥預測

2.2.1 菌群覓食算法優化的BPNN性能比較 BP神經網絡的參數設置如表5所示.

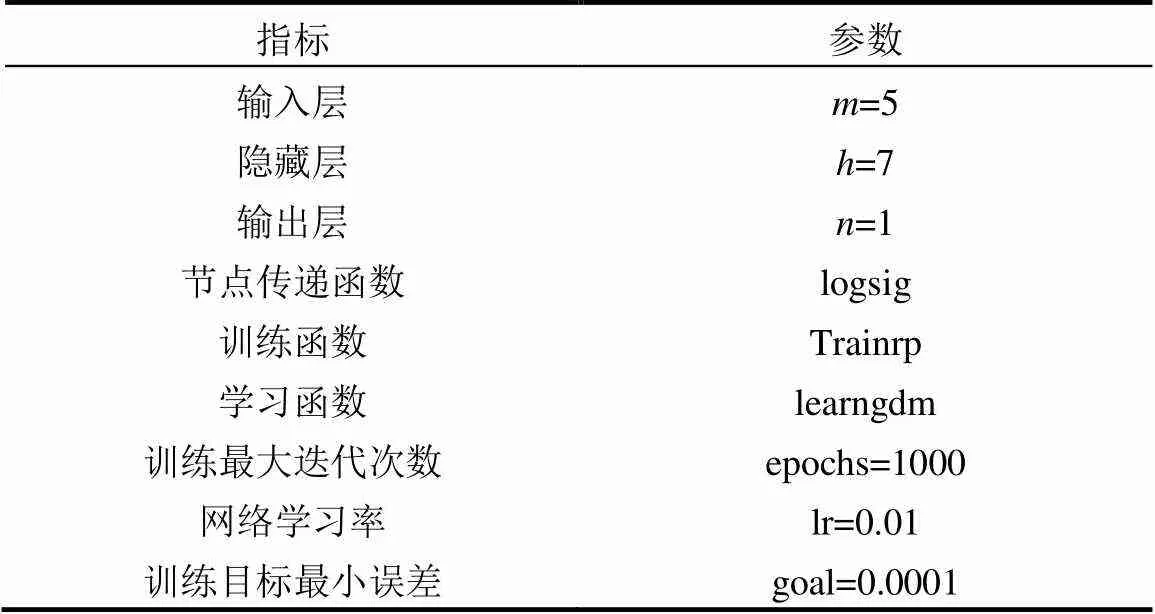
表5 神經網絡參數設置

令BPNN的損失函數為均方根誤差:

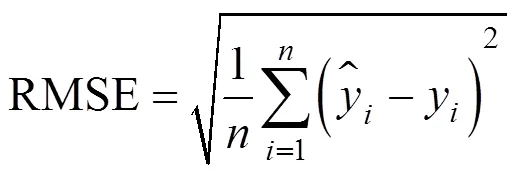
如圖5所示,通過對BPNN分別結合原始BFO、改進趨化算子的BFO、改進繁殖算子的BFO、改進遷移算子的BFO以及綜合三種改進算子的BFO的混合算法進行分析比較,綜合三種改進算子的BFO優化的BPNN(QPSO-IBFO-BPNN)對應的損失值曲線收斂效果最好.

令預測性能評價指標為MSE(均方誤差)、MAE(平均絕對誤差)、MAPE(平均絕對誤差百分比):

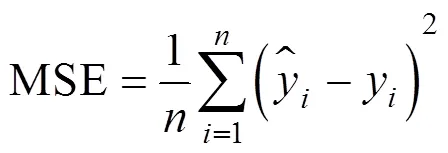
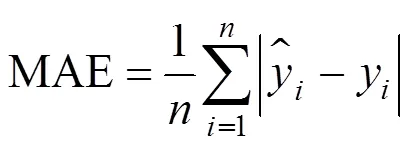
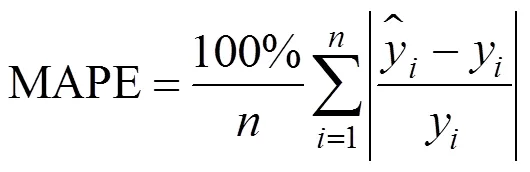
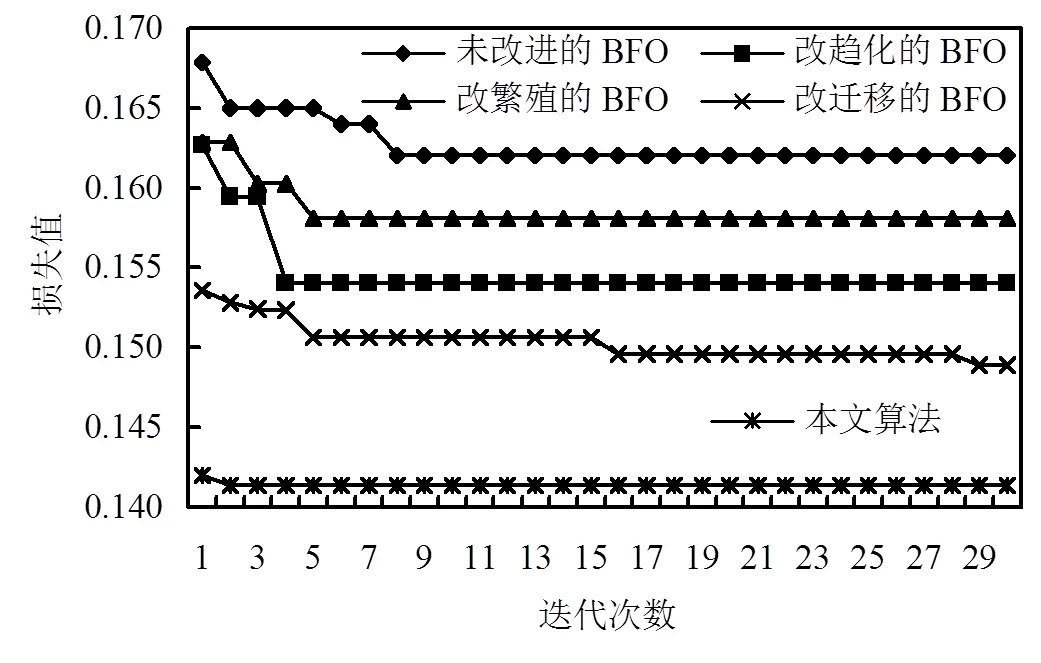
圖5 結合不同菌群覓食算法的BPNN損失值曲線

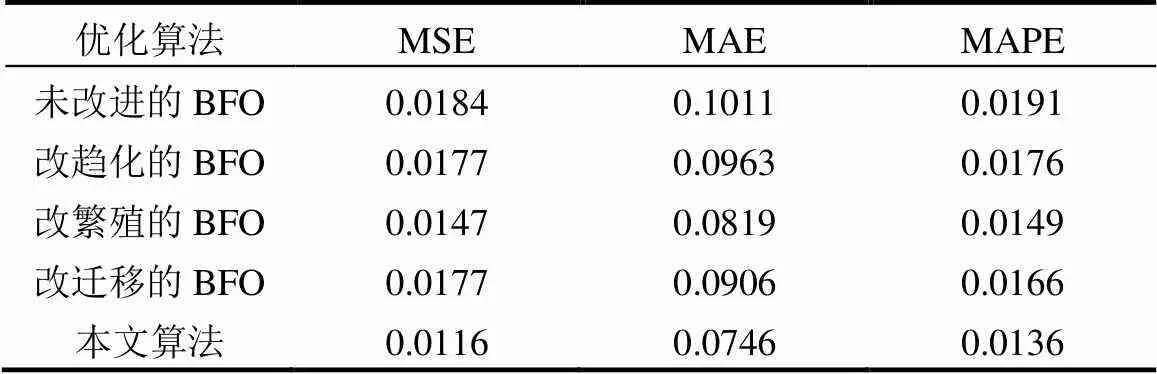
表6 結合不同菌群覓食算法的BPNN性能比較

由表6可見,改進趨化算子的BFO、改進繁殖算子的BFO、改進遷移算子的BFO以及綜合3種改進算子的BFO優化BPNN的混合算法性能均好于QPSO-BFO-BPNN,相對后者,QPSO-IBFO- BPNN性能最優,其MSE提高了34.78%,MAPE提高了28.8%.

2.2.2不同優化算法結合的BPNN性能比較 在各訓練參數相同的條件下,對QPSO-IBFO-BPNN及其對比模型進行訓練和測試,各預測模型損失值的最佳值、最差值以及平均值如表7所示.

對應損失值曲線如圖6所示,QPSO-IBFO- BPNN投藥預測模型相對于其它模型率先平穩且損失值最低.

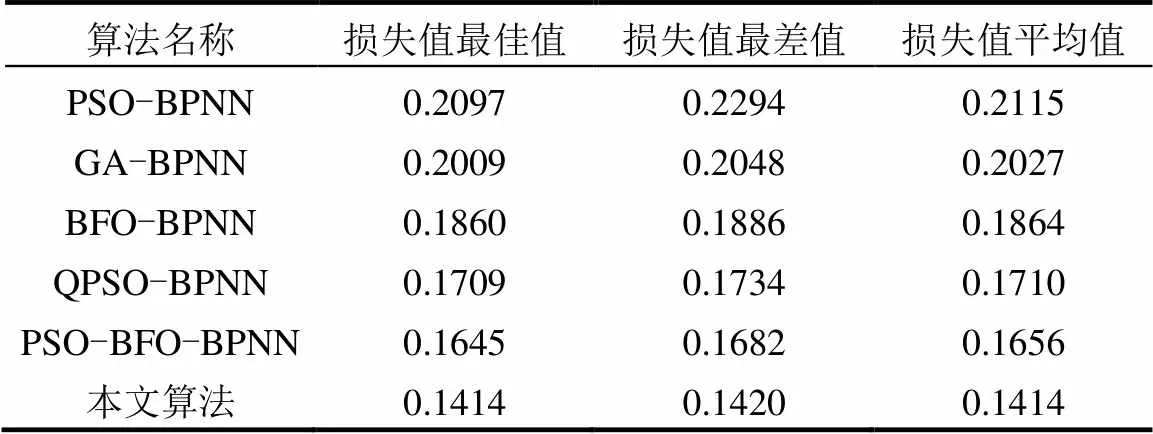
表7 結合不同優化算法的BPNN損失值

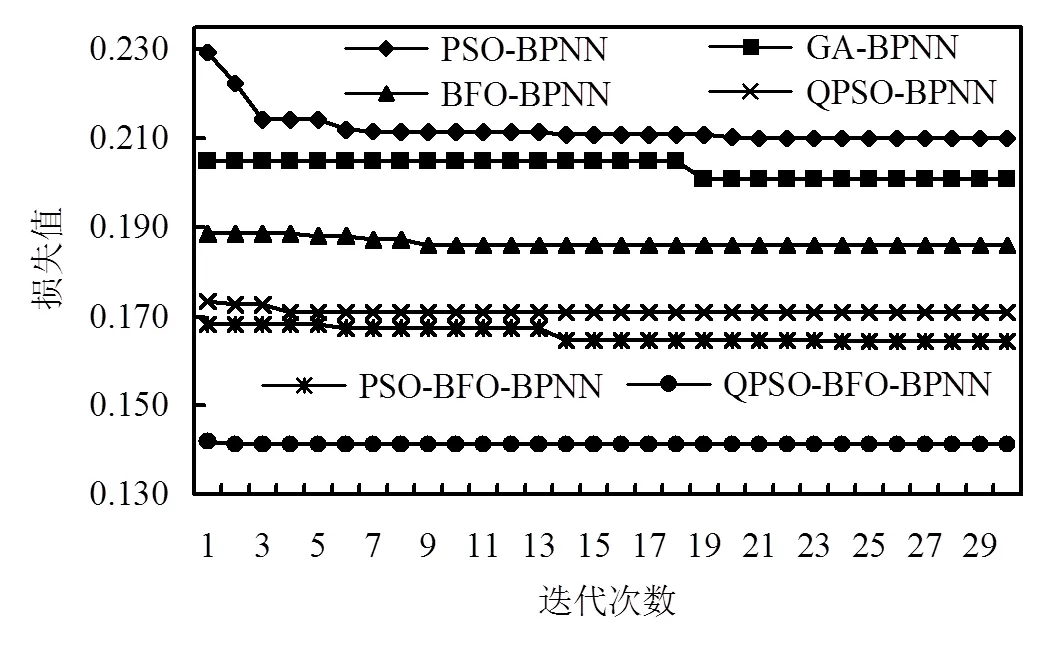
圖6 結合不同優化算法的BPNN的損失值曲線

表8為相同損失函數下,不同預測模型的性能指標.可以看出QPSO-IBFO-BPNN(本文算法)的性能最好,其MSE為0.0116mg/L,MAE (平均絕對誤差)為0.0746mg/L,MAPE為0.0136.

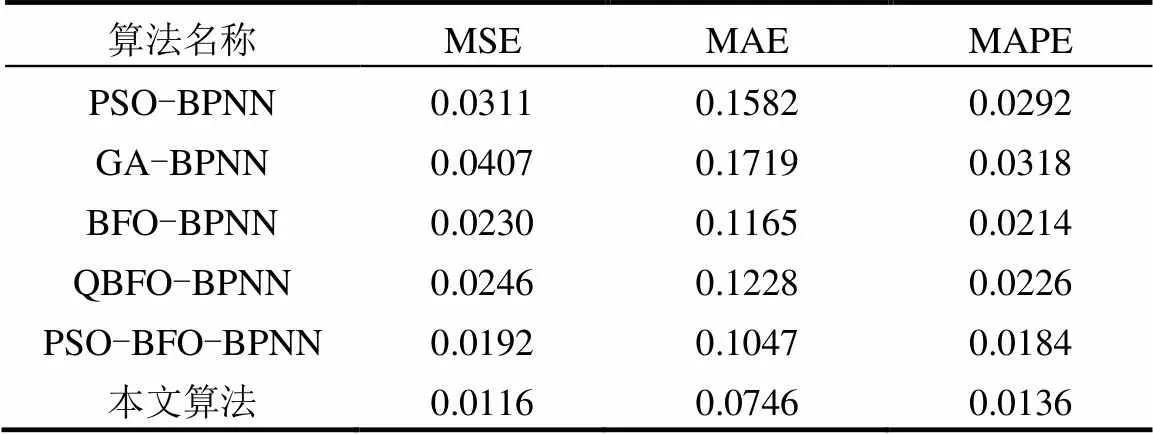
表8 結合不同優化算法BPNN性能對比

為預測模型挑選20組驗證數據如表9所示.

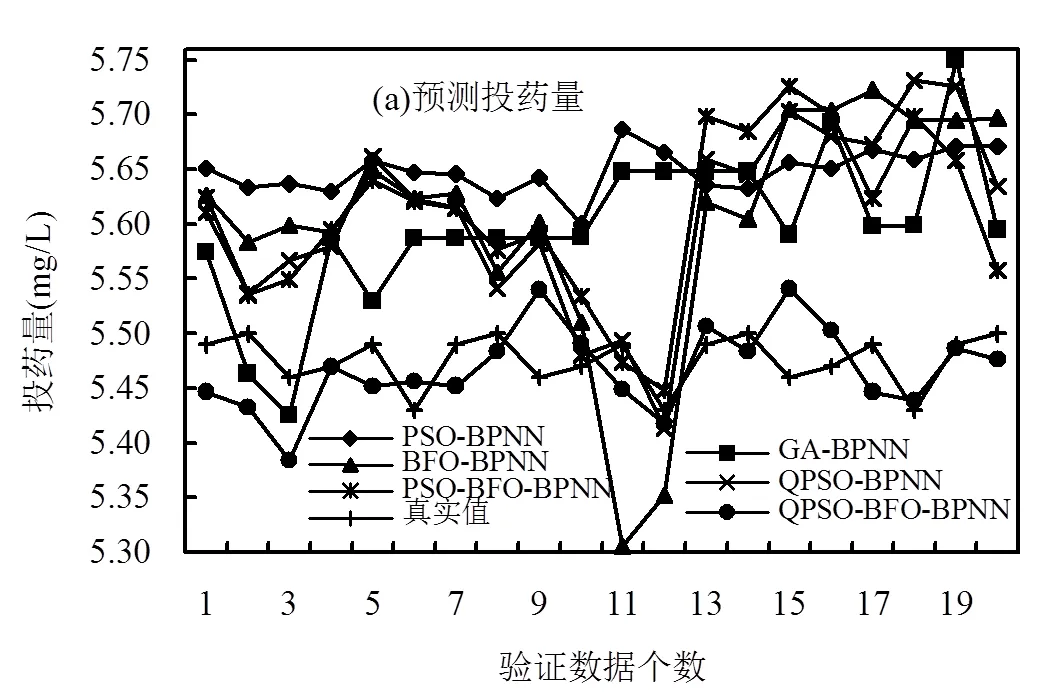
仿真實驗得到如圖7所示的分析圖.如圖7所示,可看出QPSO-IBFO-BPNN預測值與真實數據擬合度最高,其預測誤差在[-0.1,0.1]區間波動.

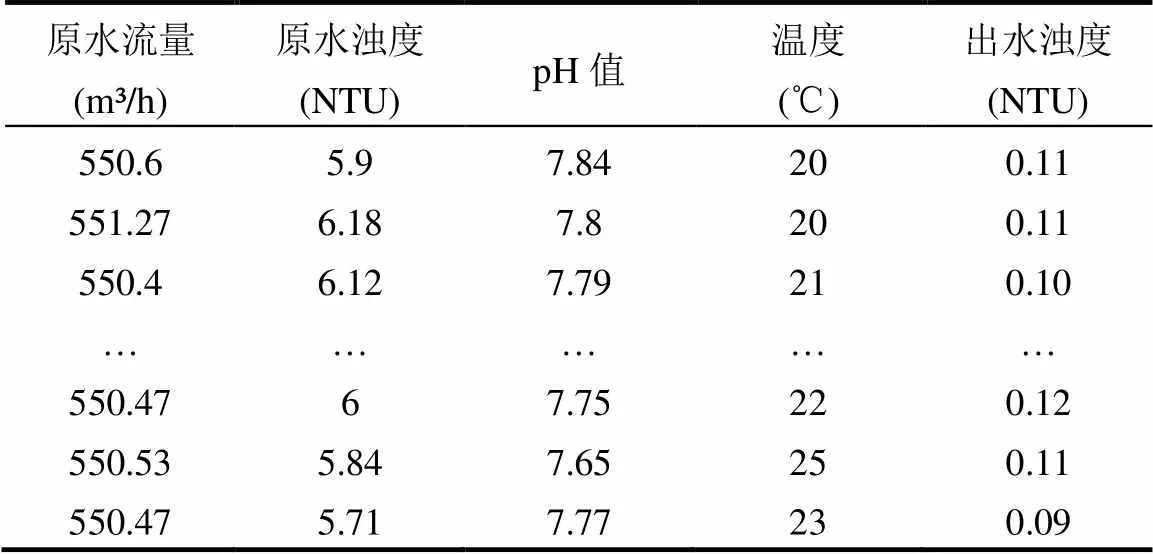
表9 驗證數據

綜上,基于混合算法預測模型的自動投藥系統能夠有效降低藥耗,減輕過濾、消毒設備的運行負擔,對達到理想混凝效果、提高水質產生了良好的經濟和社會效益.

但文中實驗僅對云南單一水廠較穩定水質數據進行仿真計算,可針對不同水源性質的多個不同處理規模的水廠、旱雨季、不同水處理工藝等情況繼續開展實驗,進一步提高非線性加藥模型的魯棒性和實用性.

3 結論

3.1 利用QPSO確定IBFO的初始值,避免了QPSO算法局部最優解的陷阱及IBFO算法的優化延遲問題,提高了IBFO算法的尋優速度,改善了其全局優化能力.

3.2 利用IBFO優化BPNN的權值和閾值,使得預測性能指標MSE達0.0116mg/L,MAE達0.00746mg/L,MAPE達0.0136,提高了非線性預測模型的擬合精度.

[1] 唐德翠,張緒紅.混凝投藥預測自抗擾工業控制器設計[J]. 控制工程, 2017,24(10):2099-2106.

Tang D C, Zhang X H. Design of predictive active disturbance rejection industry controller for coagulation dosing [J]. Control Engineering of China, 2017,24(10):2099-2106.

[2] 哀 薇,朱學峰.水廠混凝大滯后過程的數據驅動直接控制方法 [J]. 控制理論與應用, 2011,28(3):335-342.

Ai W, Zhu X F. Data-driven direct control method in water supply coagulation dosing process [J]. Control theory & application, 2011, 28(3):335-342.

[3] 白 樺,李圭白.基于神經網絡的混凝投藥系統預測模型 [J]. 中國給水排水, 2002,(6):46-47.

Bai Y, Li G B. Prediction model of coagulation dosing system based on neural network [J]. China Water & Wastewater, 2002,(6):46-47.

[4] 鄭劍鋒,焦繼東,孫力平.基于神經網絡的城市內湖水華預警綜合建模方法研究 [J]. 中國環境科學, 2017,37(5):1872-1878.

Zhen J F, Jiao J P, Sun L P. A modeling approach for early-warning of water bloom risk in urban lake based on neural network [J]. China Environmental Science, 2017,37(5):1872-1878.

[5] Chan M K, Manukid P. Prediction of settled water turbidity and optimal coagulant dosage in drinking water treatment plant using a hybrid model of k-means clustering and adaptive neuro-fuzzy inference system [J]. Applied Water Science, 2017,7(7):3885-3902.

[6] 徐少川,閻相伊,劉寶偉,等.智能控制在凈水混凝投藥系統中的應用 [J]. 中國給水排水, 2017,33(13):60-63.

Xu S C, Yan X Y, Liu B W, et al. Application of intelligent control in coagulant dosing system in a waterworks [J]. China Water & Wastewater, 2017,33(13):60-63.

[7] 饒小康,賈寶良,魯 立.基于人工神經網絡算法的水廠混凝投藥控制系統研究與開發 [J]. 長江科學院院報, 2017,34(5):135-140.

Rao X K, Jia L B, Lu L. Research and development of coagulant dosing control system for waterworks based on artificial neural network algorithm [J]. Journal of Yangtze River Scientific Research Institute, 2017,34(5):135-140.

[8] 吳曼曼,徐建新,王 欽.基于數據分解的AQI的CEEMD-Elman神經網絡預測研究[J]. 中國環境科學, 2019,39(11):4580-4588.

Wu M M, Xu X J, Wang Q.AQI prediction of CEEMD-Elman neural network based on data decomposition [J]. China Environmental Science, 2019,39(11):4580-4588.

[9] Fábio C R d S, André F H L, Cleber G D, et al. Intelligent system for improving dosage control [J]. Acta Scientiarum, 2017,39(1):33-38.

[10] 常 波,閻有運.BP神經網絡在水廠預測混凝投藥量中的應用研究[J]. 供水技術, 2009,3(5):21-25.

Chang B, Yan Y Y. Application of BP neural network for prediction coagulation dosage of waterworks [J]. Water Technology, 2009,3(5): 21-25.

[11] 伊學農,韋秋梅,何 通,等.基于GA-BP網絡混凝投藥系統預測模型的研究[J]. 化工自動化及儀表, 2009,36(2):75-78.

Yi X N, Wei Q M, He T, et al. Study of prediction modelling of coagulation dosage based on GA-BP neural networks [J]. Control and Instrument in Chemical Industry, 2009,36(2):75-78.

[12] 魏津瑜,張 瑋,李 欣.基于PSO-BP神經網絡的高爐煤氣柜位預測模型及應用 [J]. 中南大學學報(自然科學版), 2013,44(S1):266- 270.

Wei J Y, Zhang W, Li X. BFG holder forecasting model and application based on PSO-BP neural network model [J]. Journal of Central South University (Science and Technology), 2013,44(S1): 266-270.

[13] 儲 穎,邵子博,糜 華,等.細菌覓食算法在圖像壓縮中的應用 [J]. 深圳大學學報理工版, 2008,(2):153-157.

Chu Y, Shao Z B, Mi H, et al. Application of bacterial foraging algorithm in image compression [J]. Journal of Shenzhen Universit Yscience and Engineering, 2008,(2):153-157.

[14] 何偉山,秦亮曦.一種改進QPSO優化BP網絡的入侵檢測算法[J]. 計算機技術與發展, 2013,23(12):147-150.

He W S, Qin L X. An intrusion detection algorithm of BP network optimized by improved QPSO [J]. Computer Technology and Development, 2013,23(12):147-150.

[15] Yan X P, Jin P, Zhou G. An improved QPSO algorithm base on social learning and Lévy flights [J]. Systems Science & Control Engineering, 2018,6(3):364-373.

[16] Li L, Mai X F. Bacterial foraging algorithm based on quantum- behaved particle swarm optimization for global optimization [J]. Advanced Materials Research, 2013,2300:948-954.

[17] Tang W J, Wu Q H, Senior Member, et al. Saunders. Bacterial foraging algorithm for dynamic environments. in 2006 IEEE Int. Conf [C]. Evolutionary Computation, Vancouver, BC, Canada, 2006:1324-1330.

[18] Liu F, Liu Y Y, Hao H X. Unsupervised SAR image segmentation based on quantum inspired evolutionary gaussian mixture model. in 2nd Asian-Pacific Conf [C]. Synthetic Aperture Radar, Xian, China, October, 2009:809-812.

[19] Nizar H A, Farah M A. Path Planning of an Autonomous mobile robot using enhanced bacterial foraging optimization algorithm [J]. Al-Khawarizmi Engineering Journal, 2016,12(4):26-35.

[20] Mohammadi M, Montazeri M, Abasi S. Bacterial graphical user interface oriented by particle swarm optimization strategy for optimization of multiple type DFACTS for power quality enhancement in distribution system [J]. Journal of Central South University, 2017, 24:569-588.

[21] Kora P, Abraham A, Meenakshi K. Heart disease detection using hybrid of bacterial foraging and particle swarm optimization [J]. Evolving Systems: An Interdisciplinary Journal for Advanced Science and Technology, 2020,11(3):15-28.

[22] Ravi Kumar P, Naganjaneyulu P V, Satya Prasad K. Partial transmit sequence to improve OFDM using BFO & PSO algorithm [J]. International Journal of Wavelets, Multiresolution and Information Processing, 2020,18(1):1941018.

[23] Huang S R, Zhao G L. A Comparison between quantum inspired bacterial foraging algorithm and GA-LIKE algorithm for global optimization [J]. International Journal of Computational Intelligence and Applications, 2012,11(3):1250016.

[24] 2013年美國電氣與電子工程師學會進化計算大會 [S]. 2013.

2013 IEEE Congress on Evolutionary Computation [S]. 2013.

[25] 梁韓英,程曉薇,李俊鵬,等.殼聚糖聯合聚合氯化鋁強化混凝除藻的參數優化[J]. 中國環境科學, 2019,39(6):2568-2576.

Rang C Y, Chen X W, Li J P, et al. Parametric optimization of cyanobacteria coagulation by combining chitosan and polyaluminum chloride [J]. China Environmental Science, 2019,39(6):2568-2576.

Prediction model for tap water coagulation dosing based on BPNNoptimizedwith improved BFO.

ZHANG Chang-sheng1, HAN Tao1*, QIAN Bin1, HU Rong1, TIAN Hai-yong2, MAO Hui3, WANG Zhuo1

(1.Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500, China；2.Yunnan Shuye Technology Co., Ltd, Kunming 650032, China；3.Kunming Branch of North China Municipal Engineering Design and Research Institute Co., Ltd, Kunming 650051, China)., 2021,41(10)：4616～4624

In this paper, a prediction control model was proposed, which was designed with BPNN optimized by the hybrid algorithm with quantum particle swarm optimization (QPSO) and improved bacterial foraging (IBFO). In this strategy, the individual and population extremum of quantum particle swarmoptimizationwere used to update the bacterial positions in the chemotaxis process for BFO. The chemotaxis operator wasupgraded through bacteria synergy to improve the optimization accuracy. The reproduction operator was improved with difference method to solve the problem of partial dimension degradation. The roulette measure was applied as the selection mechanism to perfect the migration operator, which could overcome the disadvantage of the disappearance for the excellent solutions in the optimization process. Finally, the weights and thresholds of BP neural network were optimized to work out the coagulant dosage. Off-line training andtesting fordata model of one waterworks in Yunnan showed that the mean square error (MSE) of the prediction results of the proposed algorithm was 0.0116mg/L, and the mean absolute percentageerror (MAPE) was 1.36%, which weresuperior toBFO-BPNN and PSO-BPNN models in prediction accuracy and stability.

coagulation dosing；prediction model；BPNN；BFO；QPSO

TP273

A

1000-6923(2021)10-4616-08

張長勝(1970-),男,陜西平利人,昆明理工大學副教授,主要研究方向復雜工業過程建模、智能優化算法.發表論文50余篇.

2021-02-22

國家自然科學基金資助項目(51665025,61963022)

* 責任作者, 122832170@qq.com