基于深度學習的隨船波浪測量技術研究

張建宏，盧文月，李 欣，田新亮，郭孝先，張顯濤

(1. 上海交通大學 海洋工程國家重點實驗室，上海 200240； 2. 上海交通大學 三亞崖州灣深海科技研究院，海南 三亞 572025)

浮式海洋平臺是海洋資源生產活動的重要支撐，海洋平臺的作業安全是各類海洋活動有序進行的前提。波浪作為海洋環境中最重要的環境要素，其測量工作是浮式平臺水動力響應研究中十分關鍵的技術環節[1]。目前，對于平臺所處海域海洋波浪測量的最主要手段為波浪浮標和X波段雷達，其中X波段雷達僅能夠獲得一段時間內波高與周期的統計值，而波浪浮標不能適用于深水環境且無法隨船實時測量[2-4]。因此尋找新的技術手段實現波浪時序的隨船測量成為浮式平臺水動力響應研究中需要考慮的重要問題。

鑒于常規的測量手段對復雜實海域條件下浮式平臺所處位置真實波面升高的實時測量難度較大，根據浮式海洋平臺與波浪相互作用的機理，對平臺氣隙—運動響應數據進行推算進而獲得高精度波浪時序信息。氣隙響應及其預報方法對于波浪時序隨船測量技術的研究十分重要，近年來眾多學者通過理論研究的方法開展了氣隙預報方面的研究。對于浮式結構物如半潛式平臺來說，在平臺設計階段氣隙響應的預報是一個十分復雜的問題，與許多參數有關，包括平臺的主體特征，系泊系統的動力特性及海洋環境的特征等[5]。在平臺實時監測中瞬時氣隙響應主要受兩部分影響：平臺所處位置處的波面升高，平臺的垂向運動響應。除此之外，氣隙的動態變化還受入射波浪的非線性作用，涉及到波浪在平臺立柱之間復雜的繞射、反射作用以及平臺運動興波的影響，這種繞射和輻射波浪疊加在隨機入射波浪上會使得局部波面升高顯著增加從而減小平臺的氣隙[6]。另外，入射波與平臺立柱相互作用時存在的波浪—結構物水體共振現象，會造成局部瞬時波面升高，加上平臺系泊及立管系統的影響，大大增加了氣隙預報的難度[7-8]。采用線性分析理論遠不能滿足計算精度的要求,而二階散射方法雖然可以提高計算精度，但是會過高估計氣隙極值，其計算結果與試驗結果存在一定的差距，并不能準確預報波面升高和波浪爬升的問題[9-11]。完全非線性的求解方式雖然能夠較為精確預報平臺的氣隙分布，但因其理論模型復雜，計算量巨大，且波浪與平臺、錨泊和立管系統之間的全耦合運動大大增加了計算難度，整體預報十分困難[12]。

為確定平臺在不同極限環境條件下的水動力性能尤其是關注平臺各位置處的氣隙分布，模型試驗是目前可以準確測得隨機波浪下氣隙時歷的最常用方法。Mavrakos等[13]通過一座四立柱的浮式平臺開展了一系列規則波試驗，通過分析試驗結果認為Nielsen等[14]計算出的波浪極端非線性現象在立柱周圍尤為明顯，且采用線性繞射和輻射理論很難模擬出此非線性現象，而錨泊狀態下平臺的垂蕩運動降低了波浪的相對波面升高值。Naess等[15]對安裝在挪威海域的Kristin半潛平臺開展模型試驗研究，分別使用三參數Weibull方法和Naess-Gaidai方法，利用模型試驗測得的氣隙時歷建立統計修正模型，對半潛平臺周圍的極限波面升高進行準確統計，研究表明后一種方法在半潛式平臺氣隙預報方面更有優勢。Lu等[16]通過一座三立柱半潛式平臺的模型試驗對其波浪爬升和氣隙響應進行了研究，通過小波分析發現極端海況下氣隙響應中的高頻成分主要來自于入射波、平臺的垂蕩運動以及縱搖運動之間的耦合運動。除此之外，半潛式平臺氣隙響應的實船監測也是國內近年來逐漸開展的研究方向，蓋曉娜等[17]對安裝在中國南海的一座半潛式平臺上的傳感器在一年中采集到的氣隙數據進行了時域分析、譜分析和統計分析，提出了一些經驗性的實測氣隙數據分析方法。

針對浮式平臺所處海域波浪—結構物非線性相互作用以及傳感器測量位置偏移導致的測量誤差，利用半潛式平臺模型試驗獲得的氣隙和運動響應數據集，引入深度學習的方法對波浪—結構物相互作用過程中復雜非線性問題進行建模，開展入射波浪時序測量方法的研究。深度學習和神經網絡技術也在近年來被國內外學者用來解決海洋工程水動力響應方面的預測、解算等問題[18-22]。

1 氣隙響應數學模型

1.1 氣隙的定義

氣隙定義為海洋平臺下層甲板底部至波面間的垂直距離，平臺的靜氣隙又稱為初始氣隙，被定義為下層甲板至靜水面的垂直距離。平臺的靜氣隙是在平臺設計過程中根據極限設計狀態所能允許的最小氣隙值推算得出的重要設計因子，而實時氣隙響應可以用來衡量波浪是否發生砰擊、越浪等強非線性現象，甚至是否會對平臺結構造成破壞。

圖1表示平臺分別在靜水面和在波浪作用下的氣隙現象。在靜水中某一特定位置(x,y)的靜氣隙定義為a0(x,y)，這一距離是在平臺設計過程中通過靜水力計算確定的。在波浪作用的情況下，η(x,y,t)表示在t時刻，特定位置(x,y)處的真實波面升高；δ(x,y,t)表示平臺在t時刻相對于靜水狀態，在入射波作用下在該點的垂向運動。

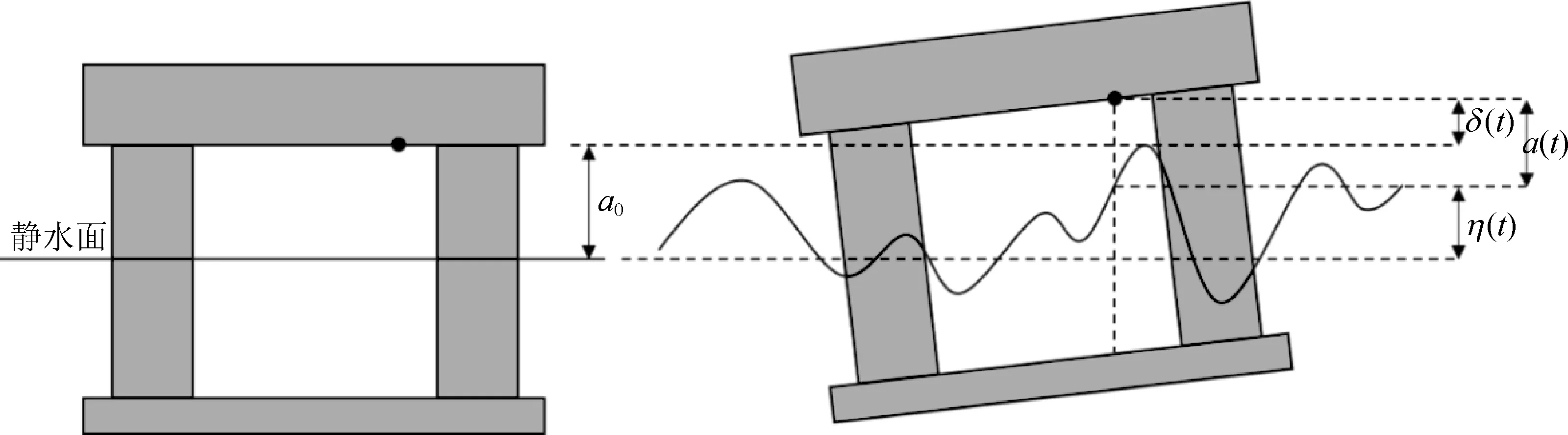
圖1 平臺在波浪中的氣隙現象Fig. 1 The air gap phenomenon of the platform in the waves

半潛式平臺的氣隙響應瞬時值主要由兩部分組成，一部分是平臺某位置的真實波面升高值，即入射波信息；另一部分是平臺的垂向運動。若平臺在自由面上做小幅運動，則基于線性理論，平臺實時氣隙響應可以表示為：

a(t)=a0-[η(t)-δ(t)]

(1)

1.2 氣隙—運動解算函數

考慮垂蕩、橫搖、縱搖運動對平臺氣隙響應的影響，以及非線性效應造成的誤差對真實波面升高的推算過程帶來的誤差，則平臺某特定位置處的真實波面升高可以表示為：

η(t)=a0+Heavep(t)-at(t)cos[ψ(t)]-εer(t)

(2)

式中：a0表示平臺的靜氣隙，也稱為初始氣隙，表征平臺下甲板至靜水面的垂直距離，是平臺設計階段按照極限設計狀態下平臺所能允許的最小氣隙值推算得出；at(t)表示測波微波雷達所測數值，由于實測中測波雷達安裝位置是固定的，所以平臺在波浪作用下產生橫搖、縱搖等運動時測波雷達的測量值并不是該位置到波面的垂直距離；Heavep(t)表示平臺氣隙測量位置處的垂蕩運動；cos[ψ(t)]表示平臺由于波浪作用時平臺的橫搖、縱搖等運動對氣隙測量的影響系數，由式(3)計算得到；εer(t)表示由于波浪—結構物之間的非線性效應造成的測量誤差。

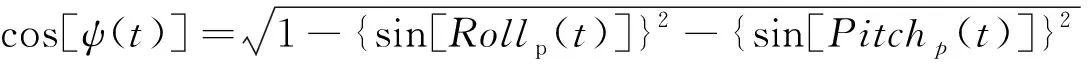
(3)

其中，Rollp(t)與Pitchp(t)分別為平臺氣隙測量位置處的橫搖、縱搖運動。因此，為了更方便對真實波面升高進行精確預測，在不考慮波浪的非線性影響下，建立氣隙—運動解算函數，以氣隙響應和運動響應作為函數的輸入值，對波面升高進行估算：

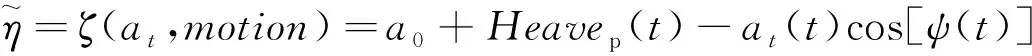
(4)

1.3 平臺運動響應空間坐標變換

在海洋平臺的氣隙實際測量中，通過GNSS-INS組合定位技術獲得的6自由度運動往往以平臺重心位置(XCOG,YCOG,ZCOG)作為參考點。為了對平臺氣隙測點(Xp,Yp,Zp)處的真實波面升高進行推算，需要將平臺中心位置的運動換算到氣隙測點位置處的6自由度運動，可以通過空間運動坐標變換來實現：

(5)

其中，

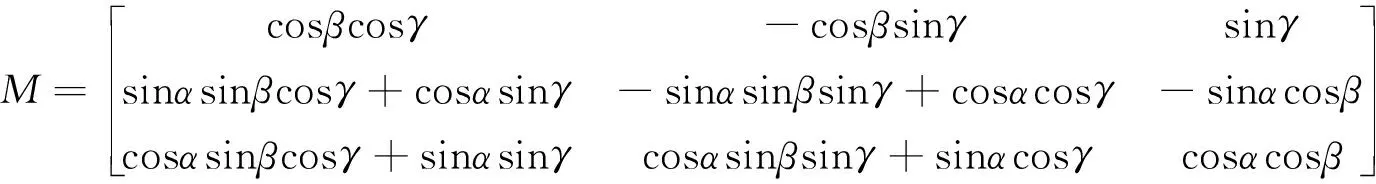
(6)

式中：α,β,γ分別是橫搖、縱搖和艏搖；SurgeP，SwayP，HeaveP分別為船體在x,y,z方向的偏移。對于浮式半潛式平臺，波浪—結構物水體共振是一種非常復雜的非線性現象，現有預報理論尚不能準確對其進行預報[8]。文中的波浪測量技術是其預報過程的逆過程，其內在機理更為復雜多變，因此利用深度學習技術強大的非線性映射能力，基于模型試驗獲得的平臺6自由度運動數據和氣隙數據，建立波浪測量的神經網絡結構。

2 半潛式平臺模型試驗

研究依托在海洋工程深水試驗池開展的陵水17-2半潛式平臺模型試驗，模型試驗的縮尺比為1∶60，該模型的主尺度如表1和圖2所示。

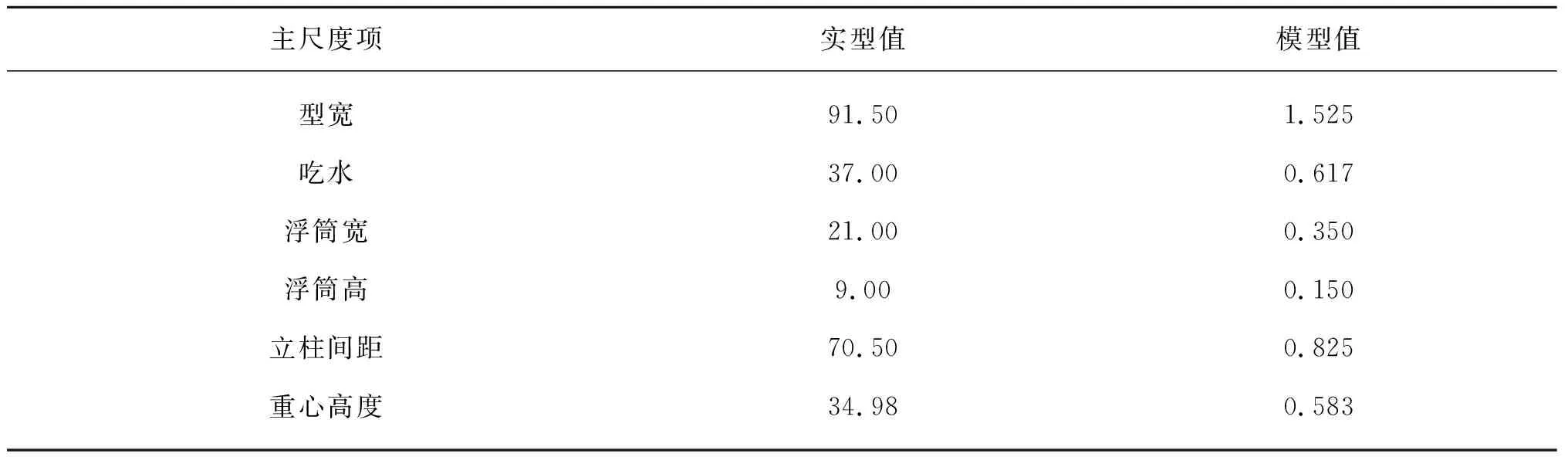
表1 陵水17-2半潛式平臺主尺度Tab. 1 Main dimensions of LS17-2 semi-submersible platform (m)

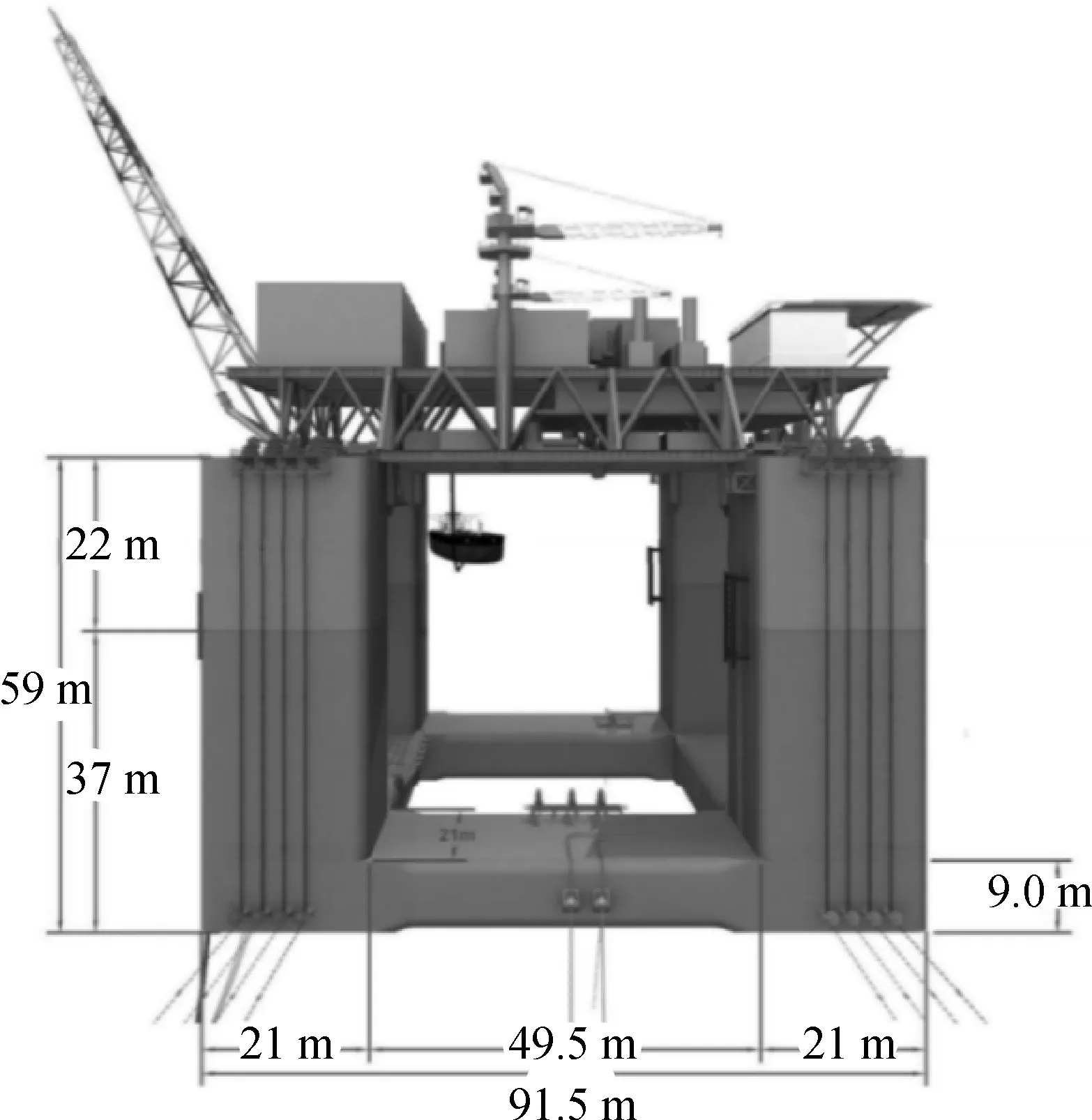
圖2 陵水17-2半潛式平臺模型Fig. 2 The model of LS17-2 semi-submersible platform

針對陵水17-2半潛式平臺依次開展了靜態剛度試驗、靜水衰減試驗、白噪聲試驗及不規則波試驗，對不同極限海況下平臺的水動力性能進行了研究[8]。試驗過程中的不規則波均使用Jonswap波浪譜進行模擬和校核。選取其中兩種不同海況開展隨船波浪測量的研究和計算，其波浪參數如表2所示。

表2 不規則波參數說明Tab. 2 Description of irregular wave parameters

在試驗校波階段，水池中央180°迎浪方向安裝的一組浪高儀用于測量水池中無結構物存在時該位置的真實波面升高，校波試驗中的波面升高與目標值的譜分析對比如圖3所示；在不規則波試驗階段，使用非接觸式6自由度運動采集與分析系統，通過運動捕捉相機對固定在平臺上的4個LED燈球構成的剛體進行識別從而獲得平臺在重心位置處的6自由度運動響應；通過在平臺各位置處安裝的電阻式浪高儀的測量，獲得了平臺不同位置處的實時氣隙響應，試驗現場如圖4所示。

圖3 校波試驗的譜分析結果Fig. 3 Spectrum analysis result of wave calibration test

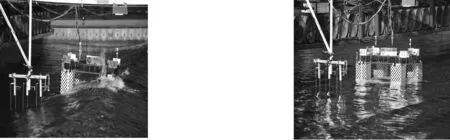
圖4 平臺在不同海況下進行不規則波試驗Fig. 4 The platform conducts irregular wave tests under different sea conditions

試驗過程中各傳感器的采樣頻率均為60 Hz，試驗結束后對兩種不同參數的不規則波試驗的氣隙、運動響應及目標真實波高數據分別進行了濾波。在試驗過程中，校波階段測得真實波面升高與基于有結構物時的波面升高測量結果并非同步測量，但由于其浪高儀位置均在平臺迎浪方向的中軸線上且十分相近，所以二者數據同步可以利用數據分析軟件通過相位調整實現。根據波浪作用于半潛式平臺的氣隙響應機理，利用氣隙—運動解算函數，利用試驗中所得氣隙響應和運動響應(主要是垂蕩、橫搖和縱搖運動)作為輸入，對平臺下層甲板某特定位置處的波面升高進行計算。

3 基于深層神經網絡的波浪時序算法

深層神經網絡是從結構、實現機理和功能上都對生物神經網絡的一種近似和模擬，由大量神經元通過復雜連接構成的自適應非線性動態系統，無需事先確定輸入與輸出之間的映射關系，僅通過自身訓練學習某種規則，在給定輸入值時獲得最接近期望輸出值的結果[23]。反向傳播(BP)神經網絡是一種按誤差反向傳播算法訓練的多層前饋網絡，其算法為BP算法，它的基本思想是梯度下降法，利用梯度搜索使神經網絡的實際輸出值與期望輸出值的均方誤差最小[24]。BP網絡可以應用于隨船波浪預測的研究中，利用神經網絡的強大非線性映射能力取代了入射波與平臺相互作用中波浪復雜非線性效應的理論模型，僅以半潛式平臺模型試驗的氣隙—運動解算函數的波高估計值和平臺運動響應作為輸入，目標真實波面升高作為輸出就可以對神經網絡實現網絡參數的優化過程，從而訓練出可以精確推算出平臺所在位置處波浪時序信息的神經網絡模型。

定義一個映射f：Ia,Im→η，其中Ia表示半潛式平臺某位置的氣隙響應，Im表示平臺的6自由度運動，η表示氣隙測點處的真實波面升高。訓練數據集向量組用{(Ia1,Im1;η1),(Ia2,Im2;η2),……,(Ian,Imn;ηn)}來表示，用于模型訓練的數據集時長為1 394 s，對應實尺度下的3 h，經過氣隙—運動解算函數的解算后，作為輸入和輸出對模型進行訓練。

圖5為整個隨船波浪預測研究過程的示意，主要包括3部分內容：1)模型試驗，波浪通過輸入造波信號，驅動水池前端的搖板造波機產生，在造波板的對岸安裝消波灘以消除波浪反射對試驗區域波動場的影響，通過傳感器及運動采集系統獲得研究所需的數據集；2)數據預處理過程，將獲得的氣隙及運動響應數據進行相位修正、濾波等處理后，利用氣隙—運動解算函數獲得波面升高的初步計算值；3)深層神經網絡模型訓練過程，利用前序步驟預處理后的輸入數據，以校波過程中的真實波面升高作為目標值計算損失函數，對神經網絡中的參數進行更新、優化。

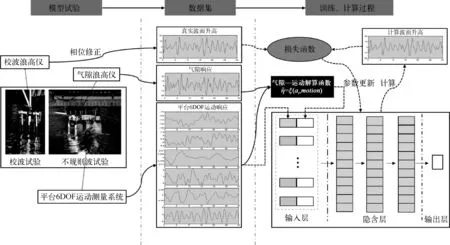
圖5 隨船波浪測量技術的流程Fig. 5 Flow chart of onboard wave measurement technology

在訓練開始前，對所有數據進行了歸一化處理，目的是消除平臺不同響應間由于本身數量級的差異而對訓練優化過程造成的影響。

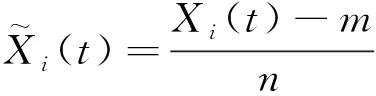
(7)

其中，m和n分別為對應輸入數據Xi(t)在30 min時間序列的平均值和標準差，在研究中均為常數，統計值見表3,其中m1,n1分別代表工況1(Hs=16.9 m,Ts=15.9 s)對應輸入數據的均值和標準差。

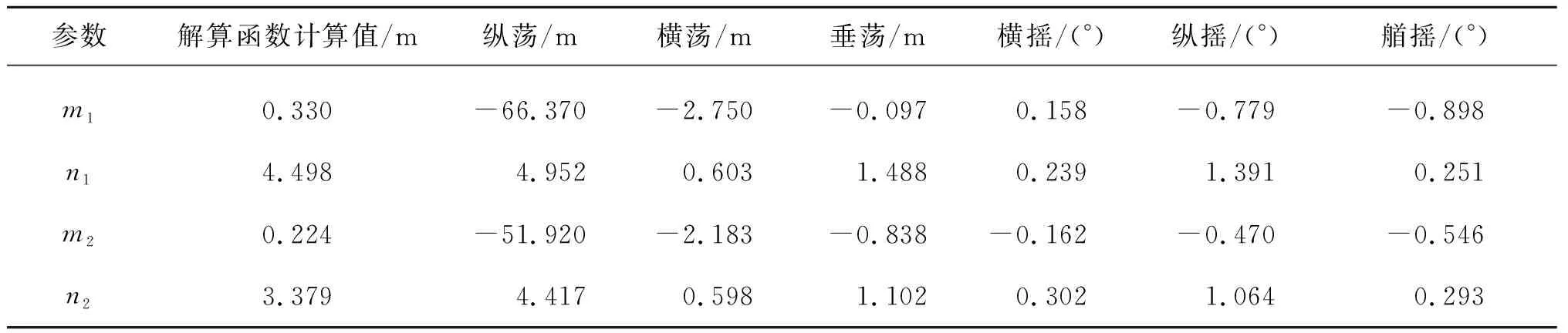
表3 輸入數據的均值和方差Tab. 3 Mean and variance of the input data

預處理后的數據集在訓練之前被劃分為訓練集和測試集，其中將工況1和工況2模型試驗數據集合并后的前70%數據用于訓練，后30%數據作為測試集。在訓練過程中，由于學習率的敏感度對模型的性能有顯著影響，選擇了自適應學習率算法RMSProp[25]，這一算法對神經網絡的參數梯度使用微分平方加權平均數進行更新，訓練中初始學習率設置為0.001，并采用均方誤差MSE作為訓練中的損失函數。

為了減少訓練過程中個別異常數據對神經網絡參數的影響，在隨機梯度下降優化中，采用了小批量隨機優化方法，批量樣本數為8。

4 波浪預測結果及驗證分析

4.1 氣隙—運動解算函數對真實波面升高的估計結果

根據剛體運動及空間坐標變換理論，考慮平臺垂蕩、縱搖、橫搖等運動對氣隙的影響得到平臺甲板底部位置處的垂向運動，建立氣隙—運動解算函數即可對該位置處的波面升高做出初步計算。

基于波浪—結構物相互作用的氣隙理論，利用氣隙—運動解算函數獲得波面升高的計算值，這一解算過程主要是將平臺的垂向運動對氣隙響應的貢獻減去，圖6分別給出了氣隙—運動解算函數計算波高和真實波面升高的時序結果和譜分析結果。對比顯示，解算波高結果與該位置的真實波面升高在時域和頻域上均存在一定的誤差，這主要是由于未考慮波浪與平臺作用的輻射、繞射等非線性效應所引起的。如圖6所示，平臺氣隙響應的頻率有3個峰值，分別在0.15 rad/s、0.50 rad/s和0.70 rad/s附近。其中在0.15 rad/s附近，平臺入射波浪在這一頻率范圍能量接近于0，而解算函數計算波高在這一范圍內還有一個峰值，但這個峰值相比于氣隙響應的峰值明顯減小；在0.50 rad/s附近，氣隙響應、解算函數計算波高及真實波面升高的能量都達到了最大峰值；在0.70～0.80 rad/s附近，氣隙響應及解算函數計算波高有一個較大的峰值，并且二者的峰值比較接近。

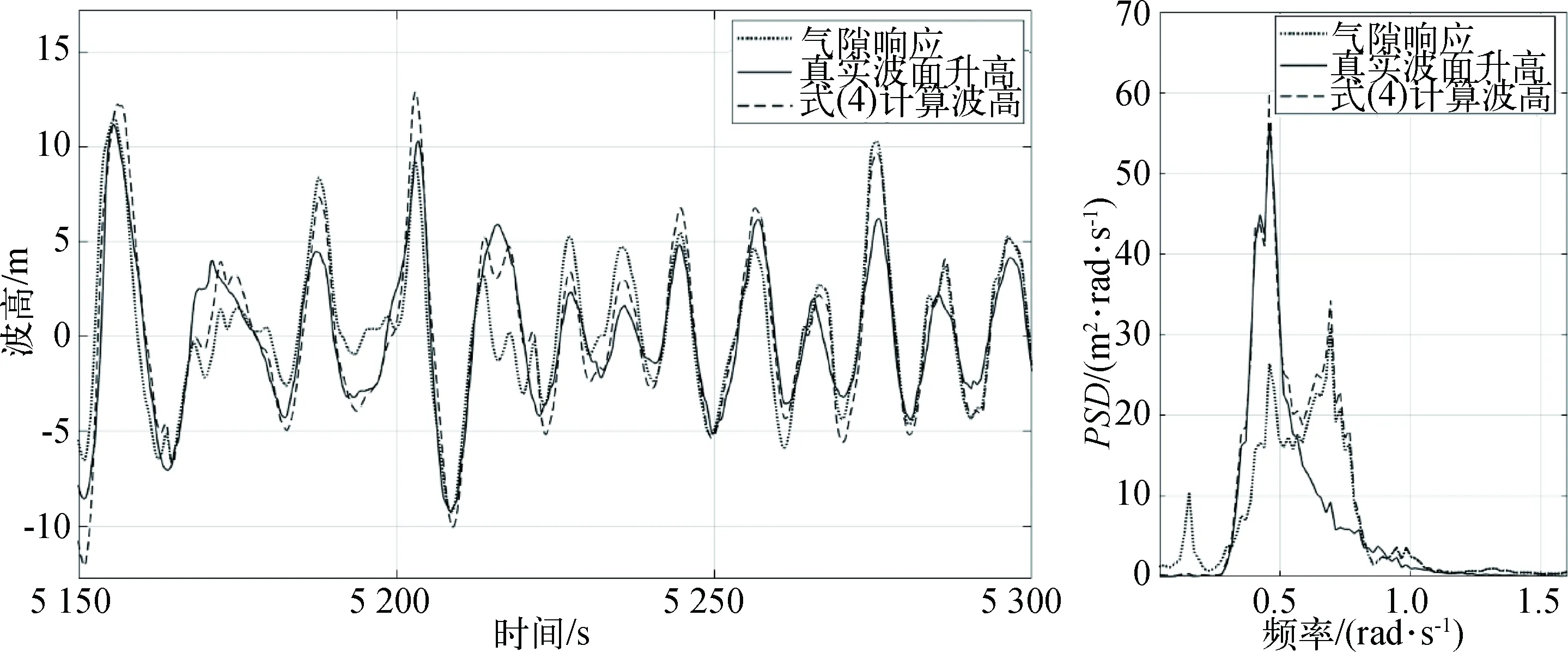
圖6 氣隙—運動解算函數計算前后的時域和頻域結果Fig. 6 Time domain and frequency domain results before and after the calculation by air gap-motion decoupling function

由于頻率0.15 rad/s與平臺的縱搖運動固有頻率十分接近，說明除了垂蕩運動的影響外，平臺的縱搖運動對垂向運動影響的權重較大，這一現象在氣隙響應的能量分布中有所體現，很可能是氣隙浪高儀的安裝位置在平臺船艏中部位置處的原因。由前述校波試驗的結果可知，0.50 rad/s是波頻部分，在這一部分，解算函數計算波高相比氣隙響應更接近真實波面升高；在0.70～0.80 rad/s附近，解算前后的譜峰幾乎完全重合，說明從氣隙中去除垂向運動對這一部分頻率的能量幾乎沒有影響，這一頻率范圍存在的能量很有可能是由于波浪與平臺相互作用中的非線性效應所產生，因此為了進一步減小波浪測量技術中存在的誤差，考慮入射波與平臺的繞射、輻射效應，采用深度學習的方法進行進一步研究。

4.2 基于深層神經網絡對真實波面升高的進一步預測結果

分別利用深層神經網絡對0°時Hs=13.4 m和Hs=16.9 m工況的真實波面升高進行預測，圖7和圖8分別展示了不同波高工況的時域預測結果。相比于氣隙—運動解算函數的計算值，深度學習的波面升高測量值顯著接近于目標真實波面升高值。

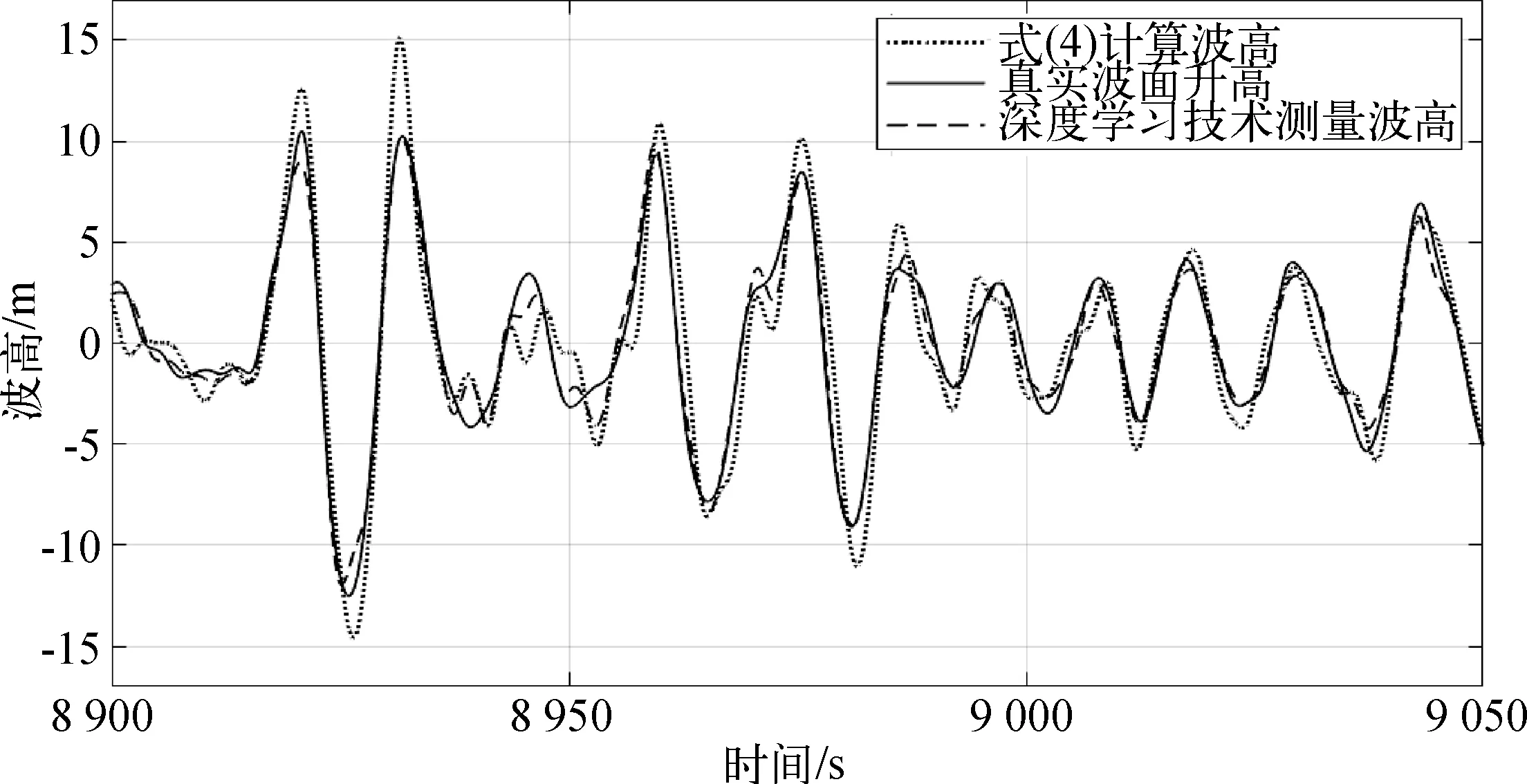
圖7 隨船波浪測量技術的時域預測結果(Hs=16.9 m,Tp=15.9 s)Fig. 7 Time domain prediction results of onboard wave measurement technology (Hs=16.9 m,Tp=15.9 s)

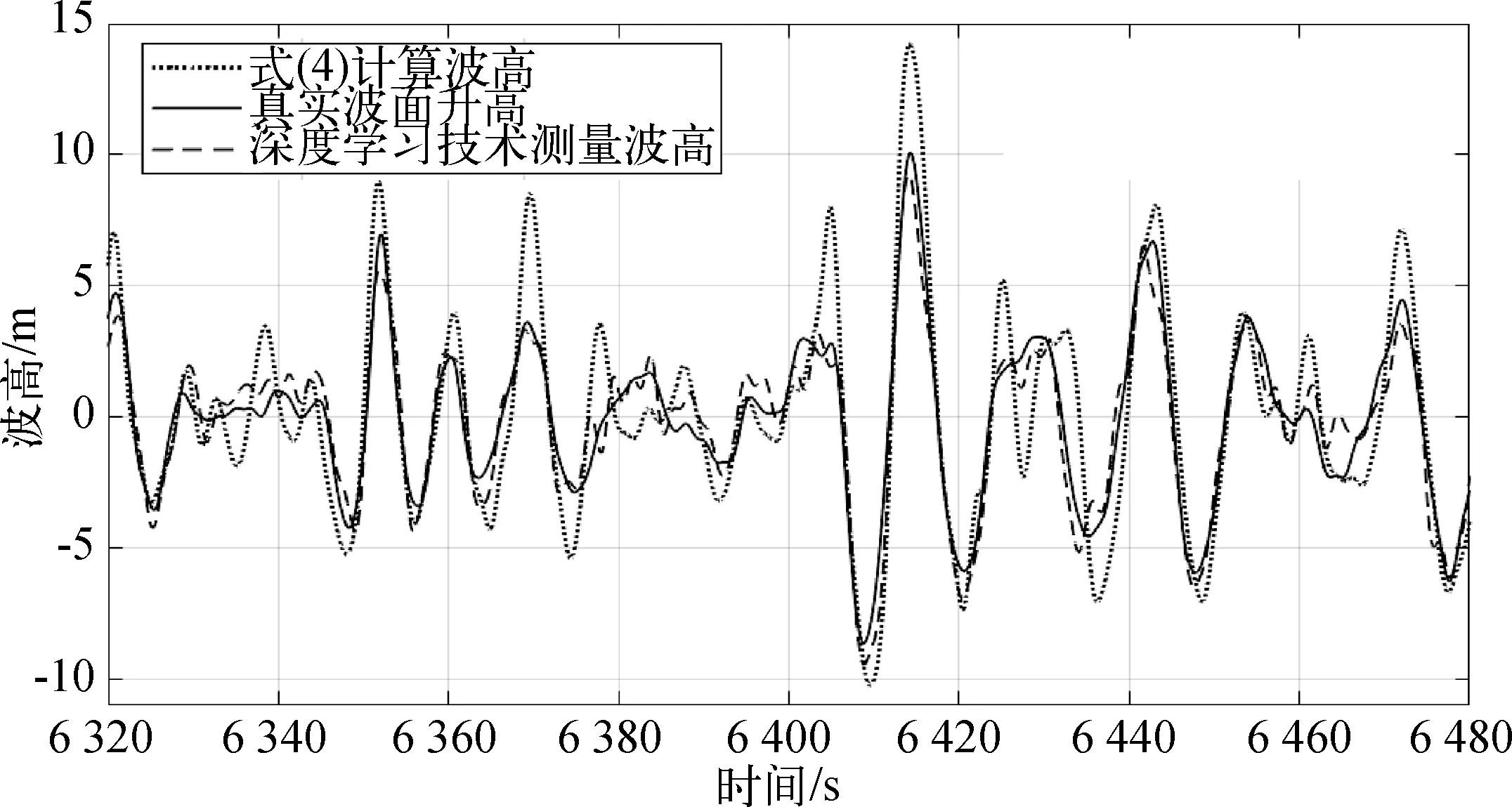
圖8 隨船波浪測量技術的時域預測結果(Hs=13.4 m,Tp=14.7 s)Fig. 8 Time domain prediction results of onboard wave measurement technology (Hs=13.4 m,Tp=14.7 s)

為檢驗深層神經網絡是否能消除由于波浪的非線性效應所帶來的誤差，圖9展示了神經網絡訓練前后的波浪時序及目標波浪時序的譜分析結果，可以看出經過深層神經網絡預測后的波面升高相對于預測前的氣隙—運動解算函數計算值，基本消除了波浪在0.50～0.80 rad/s范圍內的波浪非線性特性，與目標波高的能量分布十分接近。這一結果表明了深層神經網絡的非線性映射能力可以解決在波浪預測中遇到的復雜非線性問題。

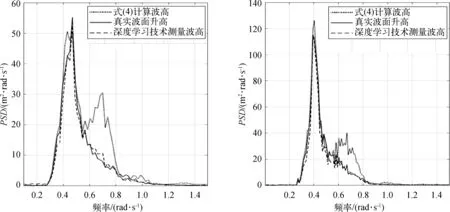
圖9 隨船波浪測量技術測量波高與目標值的譜分析結果Fig. 9 Spectral analysis results of target wave height and the value measured by shipboard wave measurement technology

對訓練前后波面升高時間序列的標準差進行了計算并比較，其結果如圖10所示，可以看出利用深層神經網絡模型訓練后的波高，其時間序列的標準差相比訓練之前的計算結果更接近真實波面升高。

圖10 波浪測量技術測量波高與目標波高的標準差結果對比Fig. 10 Comparison of the standard deviation between the wave height measured by the wave measurement technology and the target value

5 結 語

提出了一種基于深層神經網絡，利用平臺測得氣隙推算所在位置真實波面升高的波浪時序測量技術，該算法相比于線性推算方法顯著提升了波面升高在時域和頻域上的計算精度。分別選取百年一遇和千年一遇波浪工況下半潛式平臺的氣隙響應數據及運動響應數據進行神經網絡的建模，計算結果表明神經網絡模型計算波高時序相比于線性計算波高時序精度有顯著提升；在譜分析中，深度學習方法計算的波面升高依舊消除了平臺運動對波面升高低頻部分計算造成的影響，并且顯著消除了波浪—結構物非線性效應造成的波面升高高頻部分誤差，由此基于深度學習計算的波浪譜對比線性計算的波浪譜，與目標波譜在各頻域范圍內都更為接近；除此之外，對兩種計算結果分別進行統計值計算并與目標值進行對比發現，深度學習計算波高與實際波高更為接近。然而，由于實際海域中極其復雜的風浪流環境及尺度效應的存在，以及考慮到入射波浪向的復雜性，通過水池模型試驗數據訓練出的隨船波浪測量模型的適用性還需通過海上實測技術進行進一步研究和驗證。