雙浮板液艙晃蕩特性的數值研究

于曰旻

(1. 海南大學 土木建筑工程學院，海南 海口 570228； 2. 海南大學 南海海洋資源利用國家重點實驗室，海南 海口 570228)

液艙晃蕩是載液艙在外界激勵下，在部分載液率的條件下，艙內自由液面產生的劇烈波動現象。當外界激勵頻率接近于載液艙內自由液面的固有頻率時，特別是接近于一階固有頻率時，晃蕩變得尤為劇烈，巨大的沖擊載荷作用于艙壁和艙頂，往往會引起局部結構的破壞，甚至會引起整個艙體的失穩。近些年，液艙晃蕩一直是工程界和學術界的研究熱點，如何有效地抑制液艙晃蕩也成為近幾年的研究難點。

液艙晃蕩的研究方法主要包括：理論分析、數值模擬和模型試驗。除了帶有少量解析解[1]的情況之外，液艙晃蕩的研究大都采用模型試驗和數值模擬的方法。薛米安等[2]采用模型試驗的方法研究了淺水條件下液艙晃蕩沖擊壓力的特性，結果顯示一階固有頻率略大于解析解，三階固有頻率略小于解析解，而且液艙晃蕩產生的沖擊壓力隨著激勵幅值的增加而增大。楊志勛等[3]對于3個不同比尺模型，開展了高載液率液艙晃蕩的模型試驗研究，沖擊壓力和對應波形結果表明，原型(比尺1∶1)液艙中的晃蕩波攜帶大量氣泡，尤其在靜水面附近，因此沖擊效果更加顯著。此外，唐潔等[4]通過物理模型試驗，對彈性側壁液艙和剛性液艙內液體晃蕩問題進行了研究，分析兩種相對液深比條件下彈性側壁液艙與剛性液艙內不同測點的波面、振幅譜和晃動波高。基于OpenFOAM開源代碼，李金龍等[5]對比了捕捉自由液面的代數流體體積(VOF)方法和幾何VOF方法，以及在液艙晃蕩波面數值模擬方面的準確性。劉東喜等[6]通過耦合水平集與流體體積(CLSVOF)方法追蹤自由液面，對矩形液艙內三層液體晃蕩進行了數值研究，當外界激勵頻率接近于內部交界面的最低階固有頻率時，其波面會大于自由液面的波動幅度，而且流體界面會產生開爾文—亥姆霍茲不穩定性。基于移動粒子半隱式(MPS)方法，張雨新等[7]對二維矩形液艙晃蕩問題進行了數值驗證，結果表明MPS方法能夠很好地計算晃蕩產生的拍擊壓力。

目前，液艙晃蕩的制蕩結構主要分為固定式制蕩結構和浮動式制蕩結構。基于Ansys Fluent，徐毅等[8]研究了帶有底部固定擋板圓柱形臥式儲罐內的液艙晃蕩問題，結果顯示，隨著擋板高度的增加，艙壁的沖擊壓力逐漸減小，艙內波面也隨之變得平緩。基于MPS方法，Tsukamoto等[9]分析了淺水和中等水深條件下液艙晃蕩載荷與底板或者側壁肋條的相互作用。不同水深條件下，與光滑液艙相比，底板肋條和側板肋條都起到了制蕩作用，而側板肋條制蕩效果更加顯著。通過使用有限單元—光滑例子耦合方法，Zhang等[10]數值研究了底板上固定的多個彈性板與液艙晃蕩的流固耦合問題。相對于雙垂直板、雙垂直T型板和雙水平—垂直板，三垂直板制蕩效果更加顯著。Kolaei和Rakheja[11]使用有限單元法來研究在自由液面處帶有柔性薄膜的液艙晃蕩問題，在水平圓柱形液艙中，隨著薄膜張力的增加，固有頻率向高頻區移動。通過模型試驗和解析方法，Ning等[12]和Zhang等[13]分析了在自由液面處布置多層浮球的液艙晃蕩響應，隨著浮球層數的增加，晃蕩波面爬高和沖擊壓力都隨之減小。固定式制蕩結構與艙壁形成一體，安裝和維修難度較大，為了起到有效的制蕩效果，結構較為復雜，這在一定程度上減少了載液容積。浮動式制蕩結構可以隨著自由液面的變化而變化，但是當激勵幅值較大時，往往難以控制。

采用數值模擬的方法研究雙浮板液艙晃蕩特性。首先詳細介紹了數值模型，然后進行了網格收斂性驗證，對光滑矩形液艙和雙浮板液艙晃蕩波面響應進行了分析和討論，最后給出了相關的結論。

1 數值模型

為了研究雙浮板液艙晃蕩特性，采用大型商用軟件Ansys Fluent[14-15]進行二維數值模擬。不可壓縮流體的連續性方程為：

(1)

式中：ui為i方向流速。

動量方程為：

(2)

式中：ρ為流體密度；p為流體壓強；ν為流體運動黏性系數；fi為外界作用力。

Ansys Fluent使用有限體積法離散和求解納維—斯托克斯方程，流體體積模型(VOF)[16]用于捕捉自由表面，邊界條件均為固壁。對于強迫激勵下的液艙晃蕩，可以采用動量源方法[17]。6自由度求解器[18]使用力和力矩來計算物體重心的平動或者轉動，通過6自由度求解器可以限制浮板相對于液艙只發生垂蕩運動，結合動網格技術可以模擬雙浮板與晃蕩波面的耦合運動。動網格技術[19]可以用于移動或者旋轉物體周圍網格并實時更新，雙浮板周圍的網格均采用三角形網格，網格光順和網格重劃分方法得以配合使用，實時更新內部網格來阻止負網格的產生。

2 網格收斂性分析

采用的計算液艙為矩形液艙，液艙和浮板的尺寸和布置見圖1。靜止時，浮板位于自由液面處，它的密度為液體密度的一半，通過6自由度求解器，使得兩個浮板只能相對于液艙發生垂蕩運動，每塊浮板到最近側壁的距離均為L/6(L為液艙的長度)。

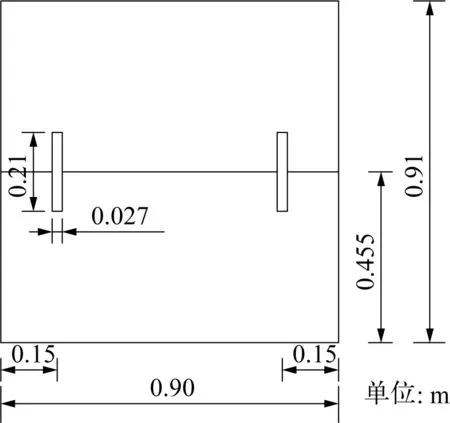
圖1 計算液艙尺寸和布置Fig. 1 Dimensions of the clean tank and layout

光滑矩形液艙的運動方程為：

U=U0sinωt

(3)

式中：U為外界激勵速度；U0為外界激勵速度幅值；ω為外界激勵圓頻率。

分別采用3種不同空間步長的網格離散計算區域，進行網格收斂性驗證[20]，分別是M1、M2和M3，離散后的節點總數和單元總數見表1。

表1 計算網格Tab. 1 Computational meshes

在載液率為50%，激勵幅值為2 mm，激勵頻率為0.84 Hz的條件下，對3個不同步長的計算網格分別開展了雙浮板液艙晃蕩的數值模擬，并提取了距離艙壁17 mm處的數值浪高儀得到的波面時歷進行了網格收斂性驗證，見圖2。結果顯示，3種不同網格的最大爬高較為一致，它們之間的相對誤差(相對于M1)均小于4%。以上對比表明，該數值模型對于網格離散不敏感，因此，為了確保數值模擬的準確性和節省計算時間，將采用網格M2開展數值模擬。

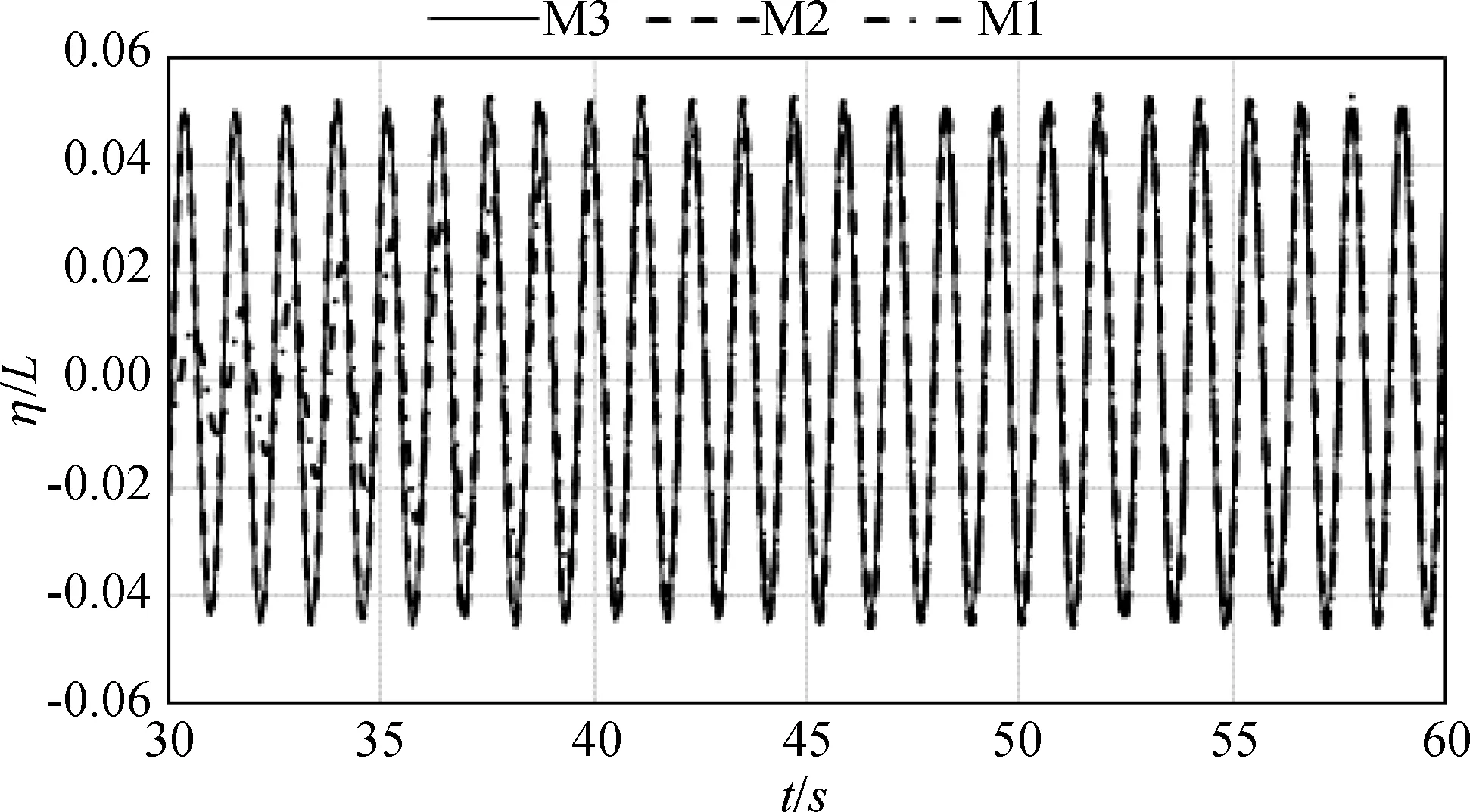
圖2 不同網格波面時歷對比(載液率50%，激勵幅值2 mm，激勵頻率0.84 Hz)Fig. 2 Wave elevation against time for three different computational meshes (50% filling rate,2 mm excitation amplitude,0.84 Hz excitation frequency)

3 結果和討論

光滑矩形液艙n階固有頻率的解析解為[21]：

(4)

式中：fn為第n階固有頻率；kn為第n階波數；g為重力加速度；d為水深。

數值模擬的計算工況見表2，載液率為50%，激勵幅值為2 mm，激勵頻率范圍為0.6～1.1 Hz(等間距為0.05 Hz)，并在一階固有頻率附近進行加密，每組運行總時間為120 s。

表2 計算工況Tab. 2 Computational cases

3.1 光滑液艙最大爬高的頻率響應

基于攝動理論，單向平動激勵下，光滑矩形液艙晃蕩波面的線性解為[22]：

(5)

(6)

當t→∞時，Bn為無窮大，此時共振現象發生。

此外，通過MTS雙向振動臺開展了光滑液艙晃蕩模型試驗，臺面尺寸為3 m×3 m，激勵頻率范圍為0～50 Hz。光滑液艙的內部尺寸為0.9 m×0.3 m×0.91 m(長×寬×高)，由2 cm厚的透明亞克力板制成，固定于雙向振動臺臺面上。浪高儀放置于液艙內，到液艙側壁的距離為1.7 cm，用來實時記錄波面。

圖3給出了載液率為50%，激勵幅值為2 mm，光滑液艙晃蕩沿艙壁爬高的最大值對頻率的響應曲線。圖3中橫坐標為激勵頻率，縱坐標為沿艙壁爬高的最大值(數值浪高儀距離艙壁17 mm)。從圖3中可以看出，解析解在一階固有頻率0.89 Hz處的爬高最大值趨于無窮大，而數值模擬結果與試驗結果吻合較好，爬高最大值先是隨著外界激勵頻率的增加而增大，在一階固有頻率0.87 Hz附近達到最大值后，開始迅速減小。數值模擬結果和試驗結果得到的一階固有頻率均略小于解析解。這里的解析解是基于勢流理論計算得到的固有頻率，忽略了波浪破碎、黏性等因素的影響。

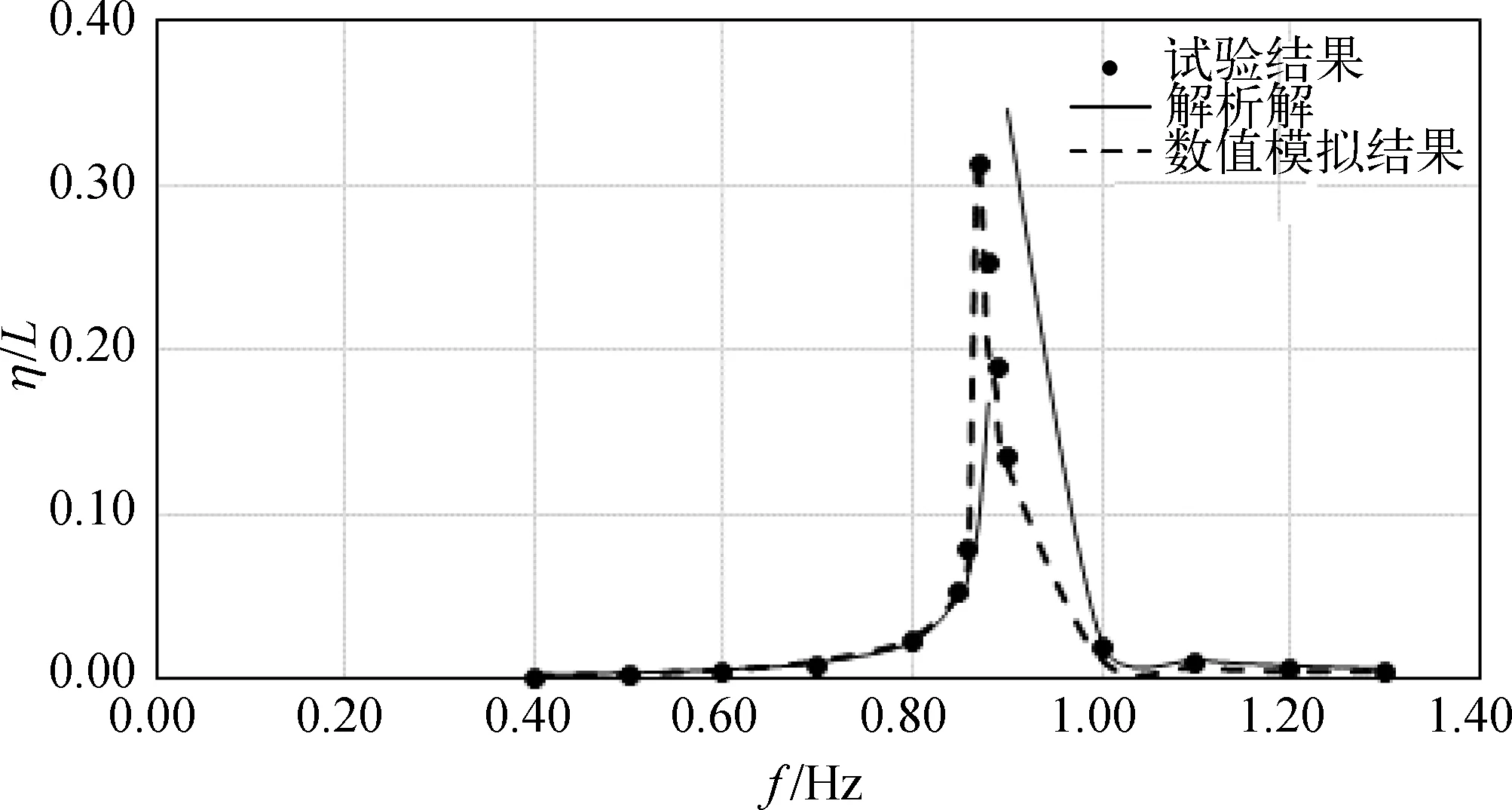
圖3 光滑液艙爬高最大值的頻率響應曲線(載液率50%，激勵幅值2 mm)Fig. 3 Maximal wave runup against forcing frequency in the clean tank (50% filling rate,2 mm excitation amplitude)

3.2 雙浮板液艙晃蕩的制蕩效果

固定式隔板需要整體固定于艙壁上。水平固定式隔板往往需要布置多層，來抑制不同載液率條件下的液艙晃蕩，因此加大了安裝和維修難度。垂直固定式隔板將液艙分為兩個或者多個子液艙，這在一定程度上減少了液艙容積。雙浮板位于自由液面處，相對于液艙只產生垂蕩運動，可以有效地抑制不同載液率下的液艙晃蕩，其安裝和維修難度相對較小，液艙的容積率也相對較大。

圖4為載液率為50%，激勵幅值為2 mm，雙浮板液艙晃蕩沿艙壁爬高的最大值對頻率的響應曲線。當外界激勵頻率小于自由液面的一階固有頻率前，最大爬高隨著激勵頻率的增加而增大；當外激勵頻率接近于0.84 Hz時，爬高達到最大值；之后，當外激勵頻率繼續增大，最大爬高逐漸減小。通過數值模擬結果顯示，光滑液艙晃蕩自由液面的一階固有頻率為0.87 Hz，與此相比，在光滑液艙中添加雙浮板之后，液艙晃蕩現象得到了明顯的抑制，最大爬高減小了83%。此外，最低階共振頻率從光滑液艙的0.87 Hz減小為0.84 Hz，說明添加雙浮板后，與光滑液艙相比，一階共振頻率會向低頻區移動[23]。

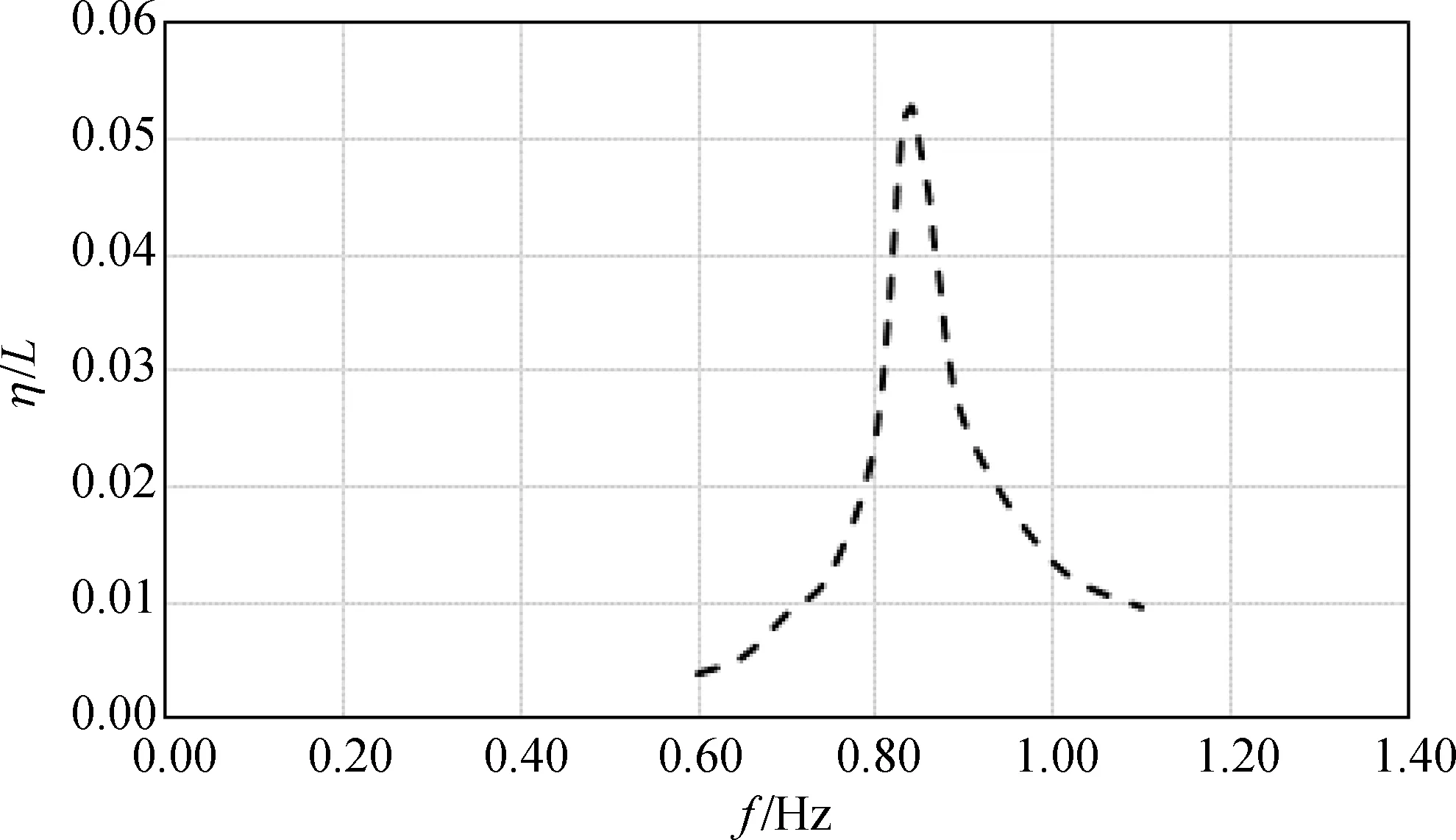
圖4 雙浮板液艙爬高最大值的頻率響應曲線(載液率50%，激勵幅值2 mm)Fig. 4 Maximal wave runup against forcing frequency in the tank with dual floating plates (50% filling rate,2 mm excitation amplitude)

圖5為數值模擬得到的雙浮板液艙晃蕩在一個激勵周期內不同時刻(T/4、2T/4、3T/4和T)的波面和雙浮板位置。如圖5所示，在t=T/4時刻，左側浮板達到垂蕩響應的最大值，此時右側浮板位于其垂蕩較小值；當t=2T/4時刻，艙內液體自由液面接近于靜水位，雙浮板均接近于垂蕩的平均位置；隨著時間的增加，在t=3T/4時刻，左側浮板達到垂蕩響應的較小值，而右側浮板位于其垂蕩最大值；當t=T時刻，艙內液體自由液面又接近于靜水位，雙浮板也均接近于垂蕩的平均位置，完成一個循環過程。此外，通過4個不同時刻的波面，液艙晃蕩模式發生了改變，由光滑液艙的駐波模式[24]變為雙浮板的U管模式[25]，這也在一定程度上起到了抑制液艙晃蕩的作用。

圖5 雙浮板液艙晃蕩在不同時刻的波面(載液率50%，激勵幅值2 mm，激勵頻率0.84 Hz)Fig. 5 Wave elevation in the tank with dual floating plates during different instants (50% filling rate,2 mm excitation amplitude,0.84 Hz excitation frequency)

4 結 語

為了研究雙浮板液艙晃蕩特性，基于Ansys Fluent建立了數值模型。通過動網格技術、6自由度求解器和動量源方法開展了雙浮板液艙晃蕩數值模擬，并進行了網格收斂性分析，通過數值浪高儀得到了載液率為50%，激勵幅值為2 mm，較寬范圍激勵頻率下液艙晃蕩的波面，并對其進行了分析，得到以下主要結論：

1) 對于光滑液艙而言，液艙晃蕩最大爬高和一階共振頻率的數值模擬和模型試驗結果吻合較好，而最低階固有頻率比解析解略小。

2) 與光滑液艙相比，添加雙浮板后，液艙晃蕩的最大爬高得到明顯抑制，對于最小固有頻率處，最大爬高減小了83%，此外，一階共振頻率向低頻區移動。

3) 不同時刻的波面顯示，雙浮板液艙晃蕩模式從光滑液艙的駐波模式變為U管模式，這在一定程度上起到了抑制液艙晃蕩的作用。