串行軸承組均載性能及承載能力分析*
盧立河,趙 晶,王世杰
(沈陽工業大學 機械工程學院,遼寧 沈陽 110870)
0 引 言
作為一種采油設備,在現階段,潛油螺桿泵采油設備需要優化的問題主要包括:井下機組下潛深度、設備工作效率以及可靠性,而增加井下機組下潛深度、提高凈揚程的關鍵難題是提升井下機組部分的軸向承載能力與耐熱性能[1]。
球鉸型自動調心聯軸體[2]承受螺桿泵的軸向載荷。根據目前的井下機組下潛深度統計,系統軸向力的總和為50 kN~120 kN不等[3],由于軸承使用工況苛刻,導致現行的標準軸承使用壽命短,承載能力不高。
王世杰、王雷[4]對潛油螺桿泵采油系統中的推力軸承進行了有限元分析,提出了改變軸承局部品質方案,但是其效果不甚理想。邱靖凇[5]提出了采用軸承串結構的方法,但由于其結構限制,僅能實現梯度分載,對于軸承承載能力的提高效果還十分有限。王世杰[6]提出了一種基于“平衡抵消”原則的雙進單出螺桿泵,但受限于國內現有的制造水平,該種螺桿泵尚未能得到實際工程應用及推廣。另外,目前還有一種方法是采用氮化硅及氧化鋯陶瓷材料制造軸承,但是受限于高昂的制造成本,使得該類軸承也難以批量投入使用。
為克服上述這一瓶頸性問題,筆者從結構設計角度出發,提出了軸承的優化設計方案,并提出了用串聯軸承組來代替單一軸承[7-12]的方案。基于“串聯結構,并行均載”的設計理念,筆者開展了針對軸承結構的創新研究,其目的是使軸承組中,各級軸承單元能夠平均承擔螺桿泵轉子反饋的軸向載荷,減少各級軸承單元的軸向載荷,以求提高軸承的可靠性,從而打破油井徑向尺寸以及下潛深度的限制,進而提高潛油螺桿泵采油系統的整體可靠性。
筆者應用數值仿真方法對軸承組的均載效果和承載能力進行研判,分析創新結構較原有結構的優化效果,提出研究潛油螺桿泵采油系統軸向承載能力的一種可行方法,為極端工況下需提高限徑軸承承載能力和可靠性的其他裝置提供借鑒。
1 串行軸承組結構及工作原理
串行軸承組(簡稱軸承組)通常采用串聯結構。此處以三級軸承組為例,軸承組的結構圖如圖1所示。
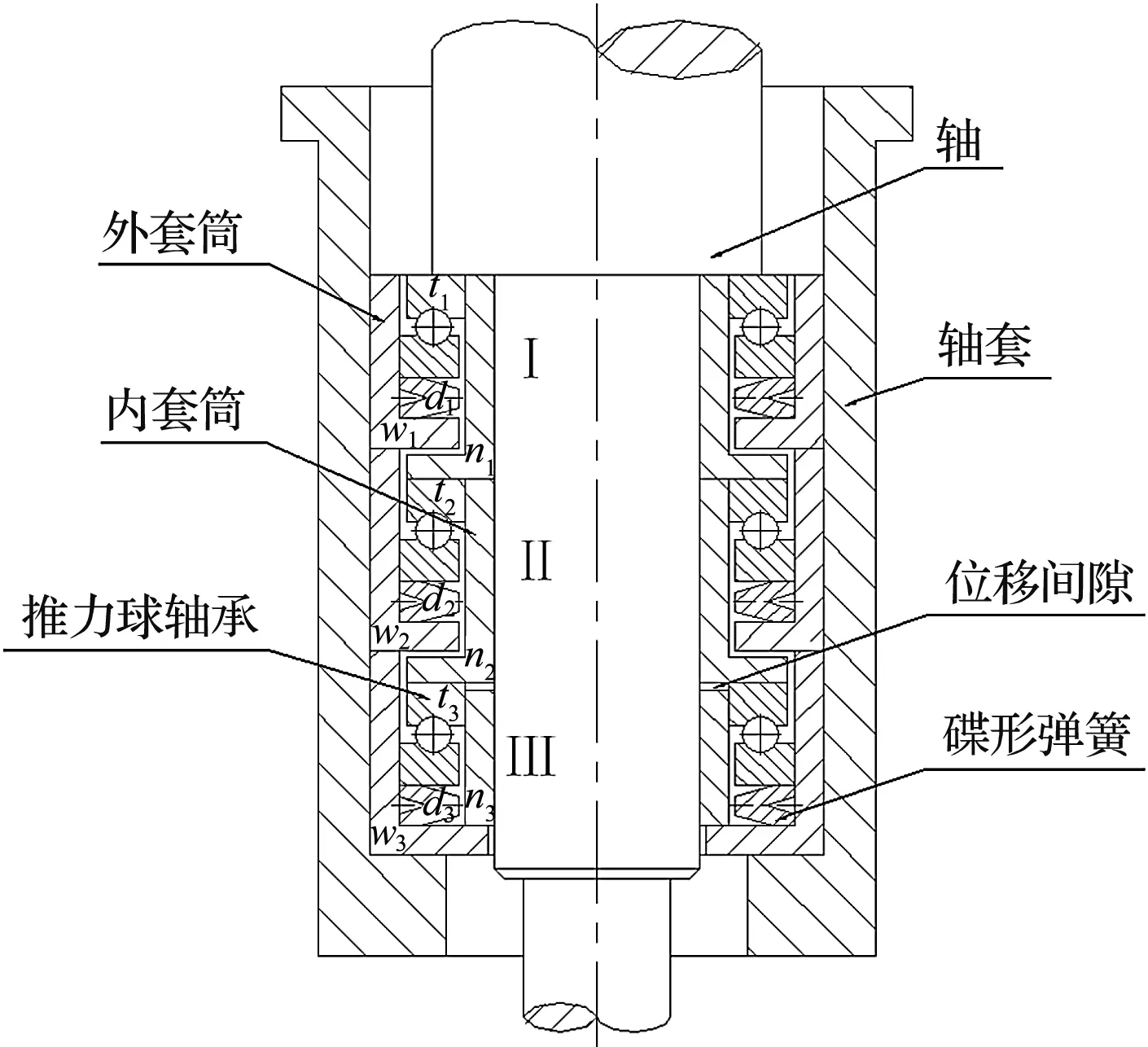
圖1 軸承組結構圖w1~w3—外套筒;n1~n3—內套筒;t1~t3—推力球軸承;d1~d3—碟形彈簧
由圖1可見:軸承組由碟形彈簧、推力球軸承、軸、軸套以及內外套筒組成,各級外套筒之間緊密連接,底座緊壓碟形彈簧、推力球軸承,起支撐定位及承載作用;各級內套筒之間僅最后一級與上一級留有軸向位移間隙,即Ⅲ級內套筒n3與Ⅱ級內套筒n2間留有軸向位移間隙,其余內套筒之間均緊密銜接,起到向下一級軸承傳遞軸向載荷的作用。
當潛油螺桿泵工作時,推力球軸承軸圈、內套筒隨軸進行回轉運動,座圈及碟形彈簧緊接外套筒固定不動,起固定支撐軸旋轉的作用,各級碟形彈簧同時開始承載變形。需要注意的是,各級推力球軸承軸圈均隨軸轉動。因此,鑒于功能實現的需要,串行軸承組內各級推力球軸承的軸圈均縮進1 mm,碟形彈簧尺寸在選取標準碟形彈簧的基礎上也經過非標加工支撐面,均不是標準件。
軸承組的工作原理是:在潛油螺桿泵采油系統開始工作時,螺桿泵轉子反饋的軸向力通過軸傳遞至Ⅰ級推力球軸承t1,同時內套筒n1受力將軸向載荷傳遞至Ⅱ級推力球軸承t2;以此類推,直至Ⅲ級,此時各級碟形彈簧承載相應的變形;當碟簧變形量累積達到軸向位移間隙時,各級軸承單元即實現了對軸向載荷的均載。
2 軸承組均載理論分析
在系統軸向載荷F(定值)作用下,軸承組中各級碟形彈簧產生軸向彈性變形;各級軸承單元滾動體與滾道面之間產生彈性接觸變形;各級內、外套筒均產生微量變形。
此處筆者采用彈性系統對軸承組進行描述,其等效力學模型如圖2所示。
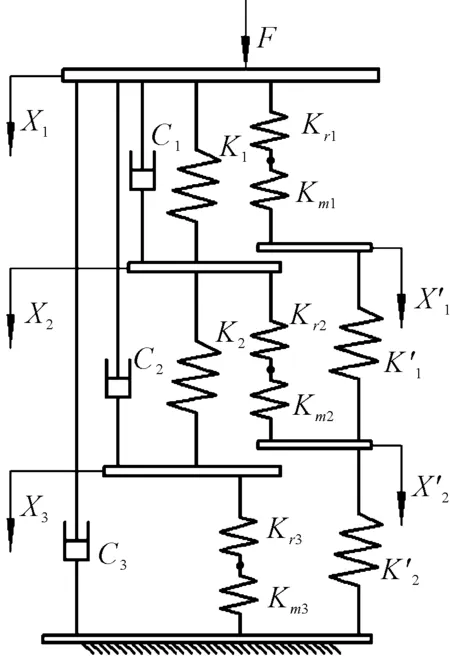
圖2 等效力學模型F—系統總的軸向載荷,N;K1,K2—內套筒的軸向剛度,外套筒的軸向剛度,N/m;Kr1~Kr3—(滾動體)接觸剛度,N/m;Km1~Km3—碟形彈簧的軸向剛度,N/m;X1~X2—碟形彈簧受載產生的變形量,內套筒傳遞載荷產生的行程,mm;C1~C3—軸承組各部件相對運動可能產生的摩擦阻尼,N,如碟簧外圓面與外套筒內圓面間相對運動可能產生的摩擦阻尼
此處應用機械阻抗分析法,得到該力學模型的等效機械網絡,如圖3所示。
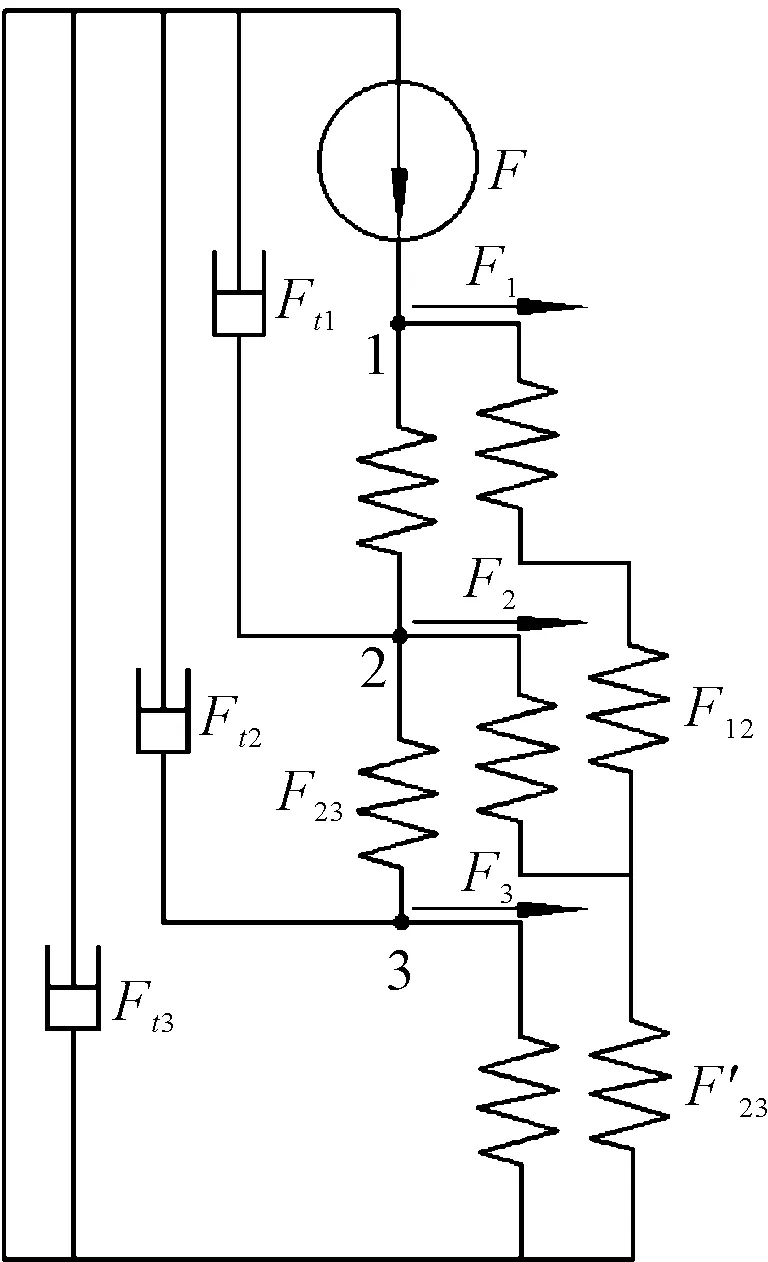
圖3 等效機械網絡F1~F3—各級軸承單元軸向力,N;F12—分載傳遞至Ⅱ、Ⅲ級軸承單元時總的軸向力,N;F23~F12—分載傳遞至Ⅲ級軸承單元的軸向力,傳遞至Ⅲ級外套筒w3的軸向力,N;Ft1~Ft3—軸承組各元件相對運動可能產生的摩擦阻力,N
在理想條件下,理論上軸承組各元件間均采用間隙配合,故本文不考慮摩擦阻力Ft1~Ft3的影響。因此,根據圖3等效機械網絡中節點力的平衡關系,可以得出1~3節點的力平衡方程組為:
(1)
要使各級軸承單元實現均載,即各級軸承單元載荷F1~F3相等,且均等于Fa/3,筆者將該值回代式(1),可得:
(2)
同理,將其推廣至Z級軸承單元構成的軸承組均載時,應有:
(3)
其中:i=1,2,3……Z-1。
(4)
已知選擇的軸承為同型號同規格,即各項參數均相等,根據上述應力公式可得到下式:
σⅠ=σⅡ=σⅢ
(5)
式中:σⅠ,σⅡ,σⅢ—Ⅰ、Ⅱ、Ⅲ級軸承單元滾動體應力值,MPa。
由式(5)可知:理論上Ⅰ、Ⅱ、Ⅲ級軸承單元滾動體應力值相等,可達到各級軸承單元接觸內載荷分布均勻性的目的,從而降低軸承組軸承單元最大接觸應力值,最終實現提高軸承壽命的目的[13]。
假定各級內、外套筒厚度相等,各級滾動體直徑相等,內套筒傳遞軸向載荷,碟形彈簧分流軸向載荷,顯然其軸向剛度必須滿足以下配比關系:
Km1=Km2……=KmZ
(6)
K1=K2……=KZ-1
(7)
3 承載能力仿真分析
為驗證軸承組結構對軸向載荷的均載效應,降低軸承組軸承單元最大接觸應力,需先對原有的單一軸承結構進行必要的仿真分析,以得出等效應力、應變,從而將其與軸承組仿真數據進行對比,進而分析軸承組結構的優化效果。
3.1 單體推力球軸承應力與應變分析
筆者選取的標準推力球軸承型號為51410。此處根據軸圈結構功能的需要,外徑縮進1 mm,因此,為區別于標準51410,筆者將該軸承命名為51410a。事實上經過仿真驗證對比,51410a與51410的軸向承載能力趨于一致,其參數如表1所示。

表1 51410a推力球軸承幾何參數
3.1.1 軸承模型的構建
考慮到推力球軸承是軸對稱結構,筆者選取軸承的1/4作為分析對象,在Creo軟件建立了51410a推力球軸承的三維幾何模型,其中,滾動體數目為8個,直徑為21.5 mm,并進行了模型簡化,依據圣維南定理[14,15],去除了對整體應力分布無明顯影響的結構。
由于推力球軸承的保持架、圓角、游隙等對應力應變的影響幾乎可以忽略不計,筆者在建模時忽略圓角、游隙等因素;同時為了建模方便,節約計算資源,忽略了保持架對有限元分析結果的影響[16,17]。
筆者將51410a三維幾何模型另存為51410a.stp格式,導入到ANSYS Workbench。材料設置為軸承鋼GCr15,由于導入的模型粗糙不便于計算求解,此時需要對模型進行拓撲優化處理;由于軟件無法自動識別導入模型為四分之一,需對模型進行軸對稱設置,新建Cylindrical坐標系設置軸對稱,利用Symmetry功能設置軸對稱;單元類型選擇為8節點solid45號單元,在此基礎上筆者用網格劃分功能自動生成網格,共劃分了23 913個網格單元,生成了52 361個節點。
3.1.2 載荷與約束施加
筆者模擬軸承的實際工況、裝配條件,在軸承座圈底部施加固定約束,對頂部模擬軸施加21 500 N的軸向載荷,軸徑為100 mm。
3.1.3 接觸對設置
接觸對的設置是軸承接觸分析的重要環節,根據接觸對指定原則[18],筆者設置滾動體表面為接觸面,軸圈、座圈滾道面為目標面;設置滾動體與軸圈、座圈滾道面接觸類型為Frictional,考慮滲砂、高溫、重載及脂潤滑條件,設置滾動摩擦系數為0.1。
3.1.4 結果分析
經ANSYS Workbench軟件分析計算所得51410a推力球軸承仿真結果如圖4所示。

(a)51410a等效應力
從圖4中可以看出:(1)51410a等效應力最大值為586.05 MPa,主要集中在滾動體與滾道面接觸位置;(2)等效應變最大值為0.003 962 8,主要集中在滾動體與滾道面接觸位置。
3.2 軸承組承載能力分析
為與上述單體軸承作對比,本文采用51410a軸承對軸承組進行仿真計算,以得出軸承組的等效應力、應變值,據此分析軸承組結構的優化效果。
軸承組的幾何特征參數如表2所示。
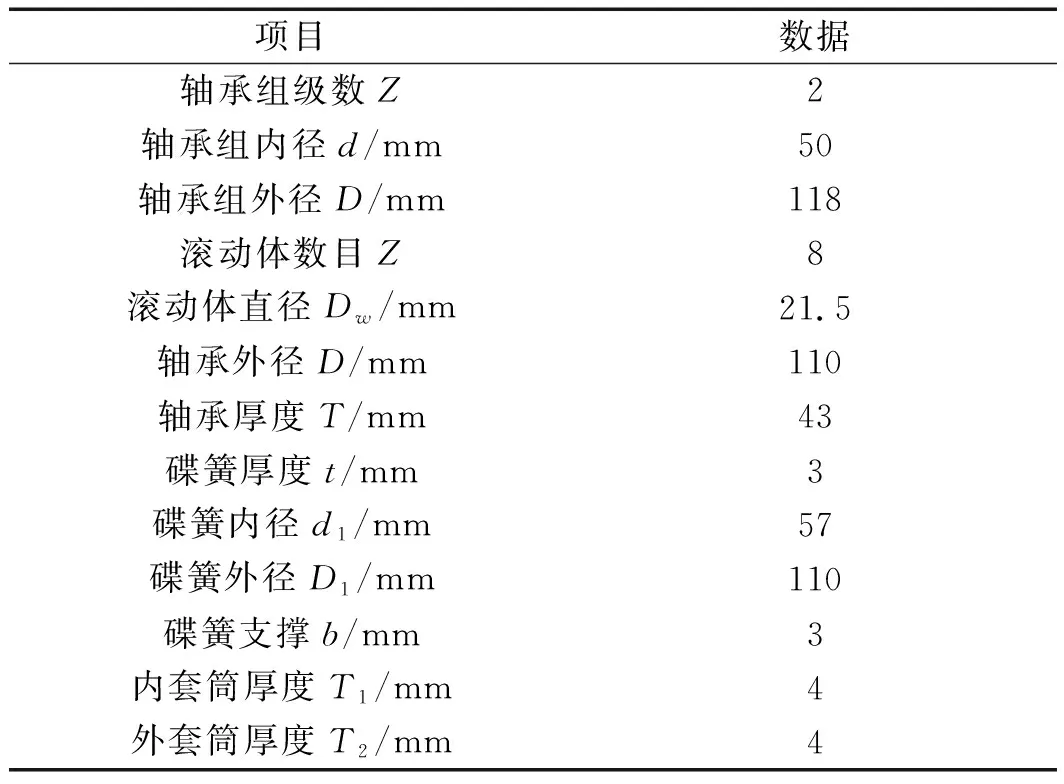
表2 軸承組幾何特征參數
3.2.1 二級軸承組仿真及結果分析
(1)軸承組模型的構建
軸承組是具有高度非線性行為的多對接觸單元的組合體,考慮到整個軸承組是軸對稱結構,筆者取整個軸承組模型的1/4進行數值模擬分析;為了建模方便,節約計算資源,進行模型簡化,去除對整體應力分布無明顯影響的結構,筆者作如下的設定[19]:略去軸套及保持架不計;不計軸承組的自重;略去倒角、圓角、游隙等不計。
將軸承組幾何模型導入到ANSYS Workbench仿真軟件中的Static Structural模塊,以及設置軸對稱、拓撲優化等過程,均與上述單體軸承的仿真過程相同,因此此處本文不再贅述。需要指出的是,軸承組碟簧采用一級對合組合型式,為便于仿真分析,筆者將碟簧對設置為一體。
再依次設置軸承組材料:軸承材料為軸承鋼GCr15,碟簧材料為彈簧鋼60Si2Mn,內外套筒及軸材料均為45鋼;單元類型選擇為8節點solid45號單元,在此基礎上用網格劃分功能自動生成網格,共劃分39 232個網格單元,生成124 891個節點。
(2)載荷與約束施加
筆者模擬軸承組的實際工況、裝配條件,軸承組外套筒底面、外圓面施加固定約束,軸承組頂部模擬施加21 500 N的軸向載荷,軸徑為100 mm。
(3)接觸對設置
多零件表面發生接觸時,筆者根據接觸對指定原則,設置滾動體表面為接觸面,軸圈、座圈滾道面為目標面,其余設置均遵循指定原則;設置滾動體與軸圈、座圈滾道面接觸類型為Frictional,考慮滲砂、高溫、重載及脂潤滑條件,設置滾動摩擦系數為0.1;外套筒與碟簧及內套筒、外套筒之間、軸承與碟簧、軸與軸承的接觸類型均設置為Bonded;碟簧與外套筒,內套筒與軸、軸承的接觸類型均設置為No Separation。
(4)結果分析
二級軸承組仿真分析結果如圖5所示。
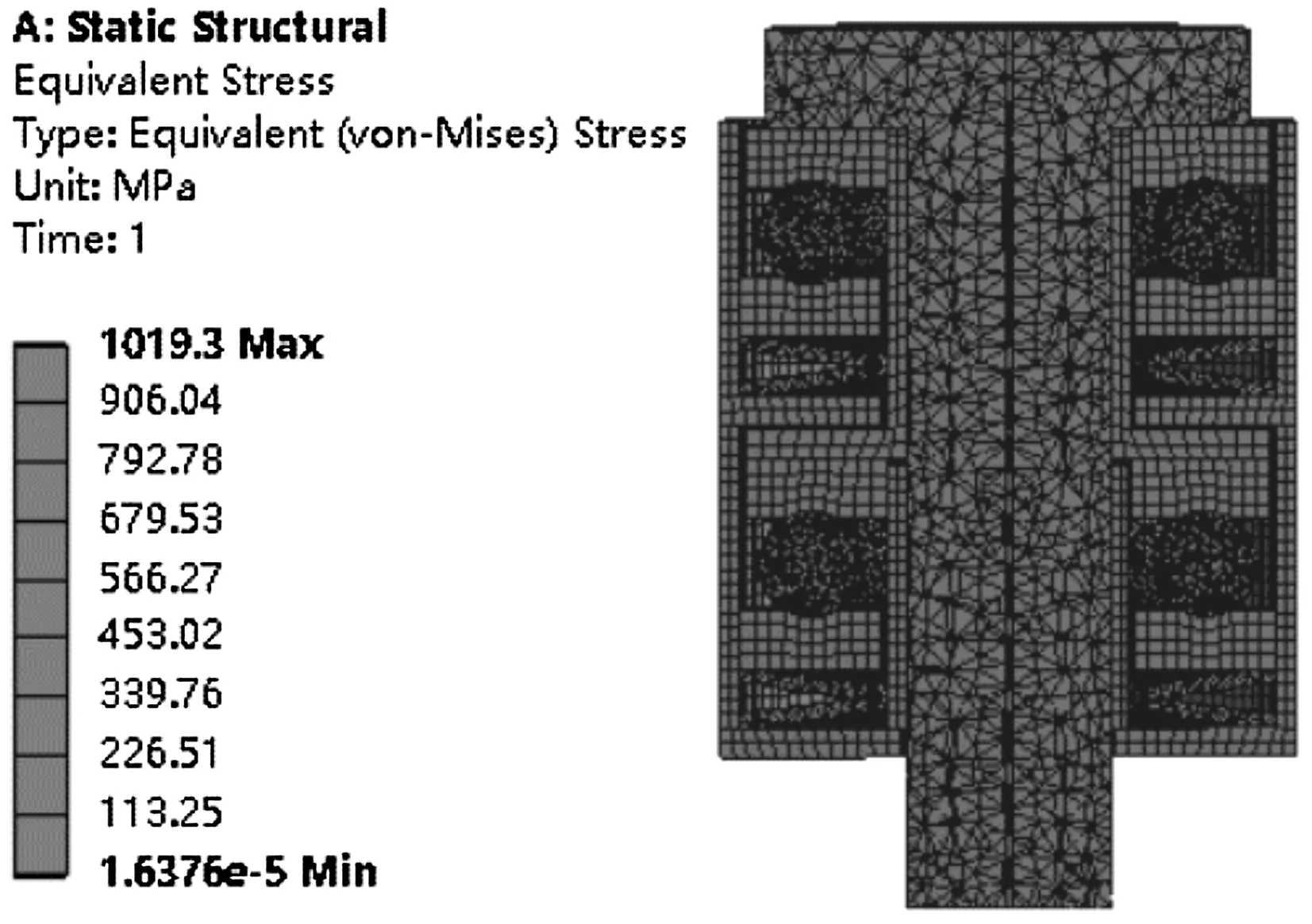
(a)二級軸承組等效應力云圖
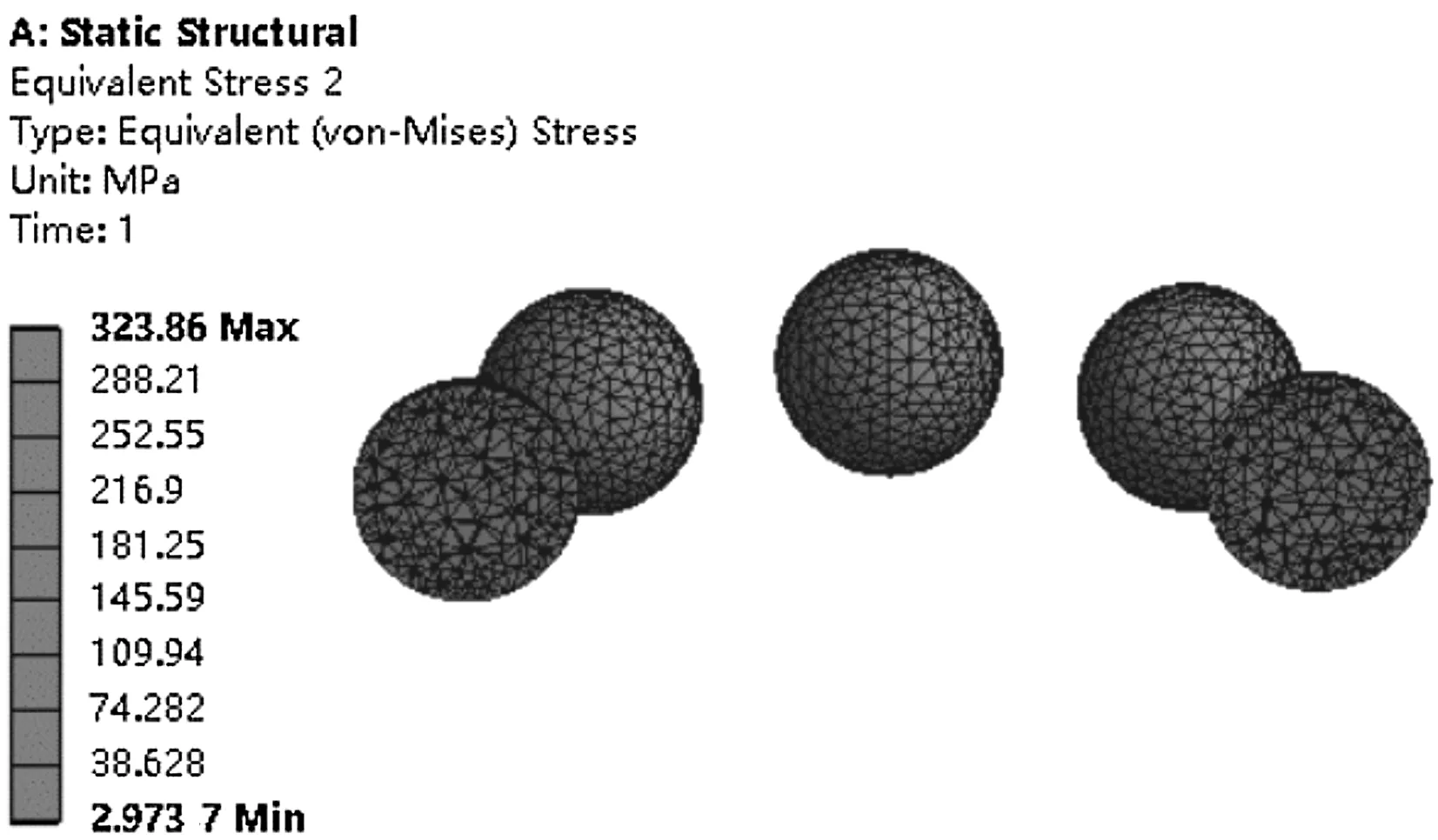
(b)第一級軸承單元滾動體等效應力云圖
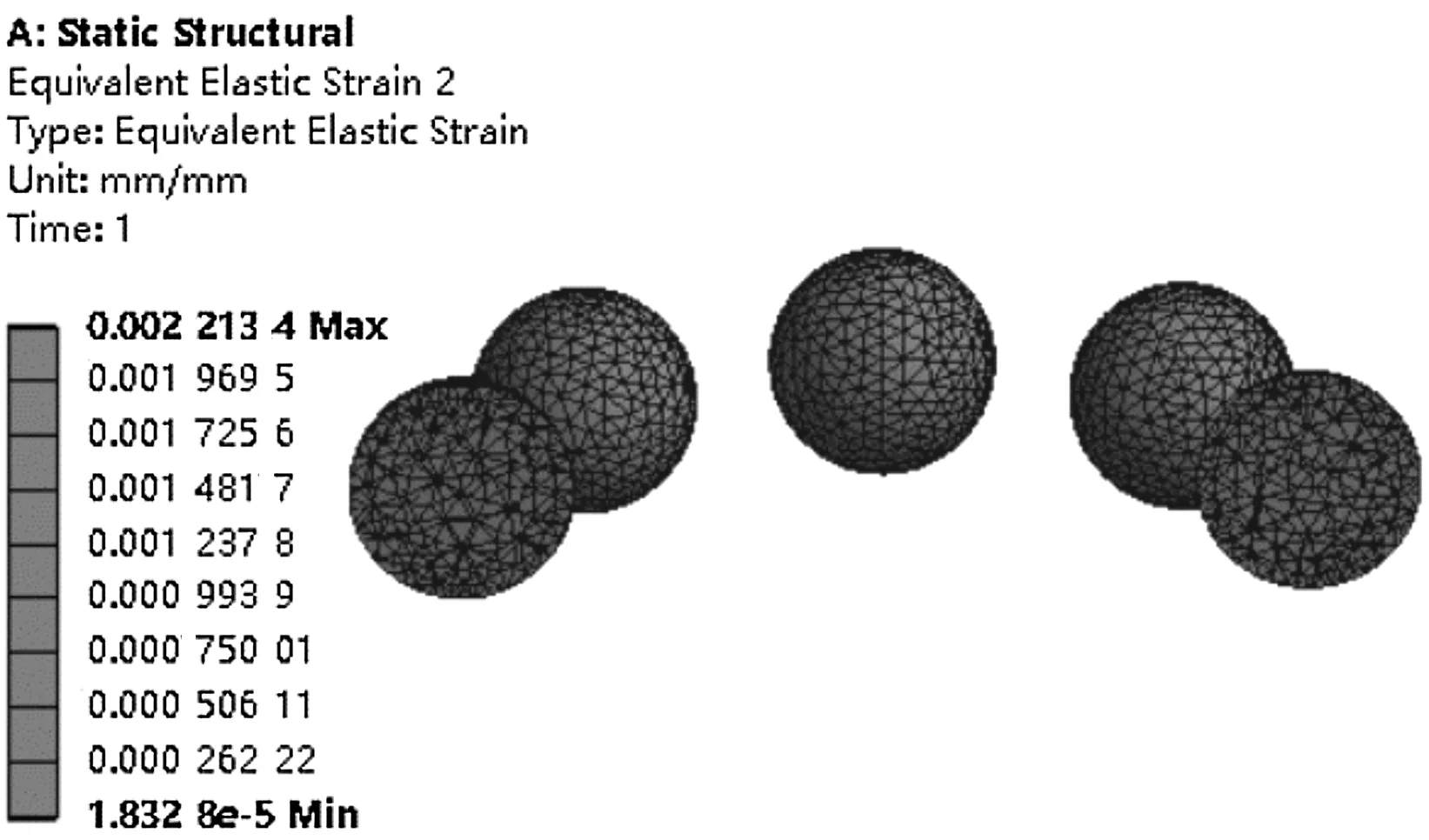
(c)第一級軸承單元滾動體等效應變云圖
由圖5可知:(1)軸承組等效應力最大值為1 019.3 MPa,主要集中在第一級碟簧對間的接觸區域,這是因為碟簧對間接觸面積小而產生的應力集中現象;(2)第一級軸承單元等效應力最大值323.86 MPa,同理第二級軸承單元等效應力最大值為329.6 MPa,均集中在滾動體與滾道面接觸區域;(3)第一級軸承單元等效應變最大值為0.002 213 4,同理第二級軸承單元等效應變最大值為0.002 424 2,均集中在滾動體與滾道面接觸區域。
3.2.2 三級軸承組仿真及結果分析
三級、四級、五級軸承組的具體仿真分析過程均與上述二級軸承組的分析過程相同,因此,此處筆者不再贅述。
三級軸承組的仿真分析結果如圖6所示。

(a)三級軸承組等效應力云圖

(b)第一級軸承單元滾動體等效應力云圖
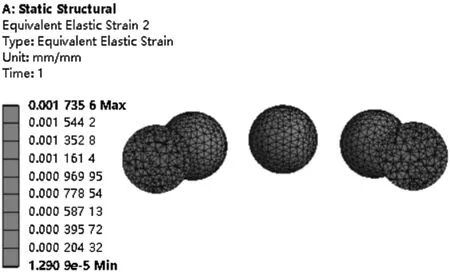
(c)第一級軸承單元滾動體等效應變云圖
由圖6可知:(1)三級軸承組最大等效應力為708.26 MPa,主要集中在第一級碟簧對間的接觸區域;(2)第一級軸承單元等效應力最大值為232.27 MPa,同理第二、三級軸承單元等效應力最大值分別為225.85 MPa、223.14 MPa,均集中在滾動體與滾道面接觸區域;(3)第一級軸承單元最大等效應變為0.001 735 6,同理第二、三級軸承單元最大等效應變分別為0.001 689 7、0.001 681 5,均集中在滾動體與滾道面接觸區域。
3.2.3 四級軸承組仿真及結果分析
四級軸承組的仿真分析結果如圖7所示。
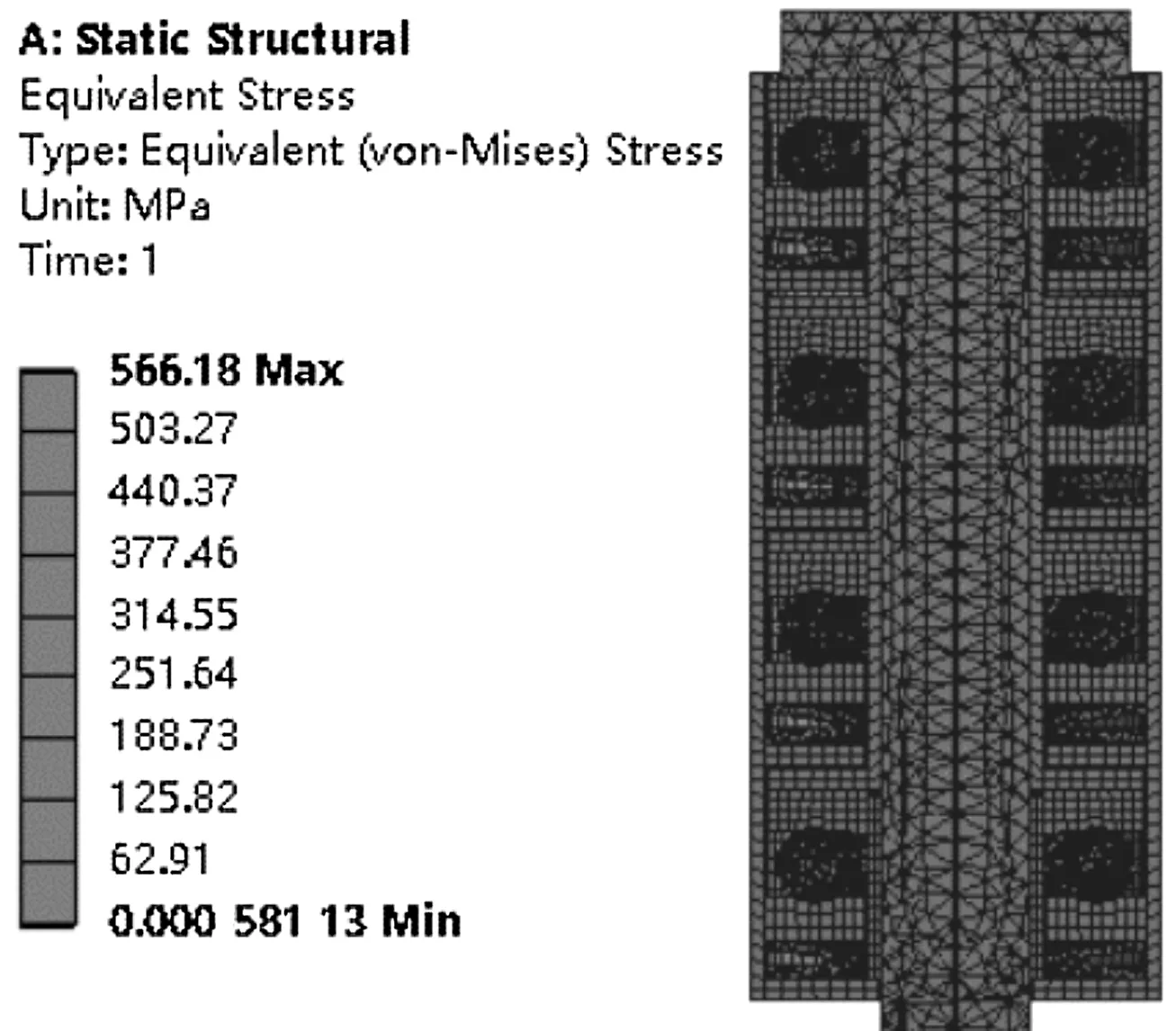
(a)四級軸承組等效應力云圖體等效應力云圖
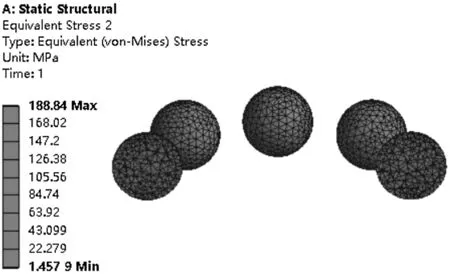
(b)第一級軸承單元滾動體等效應力云圖
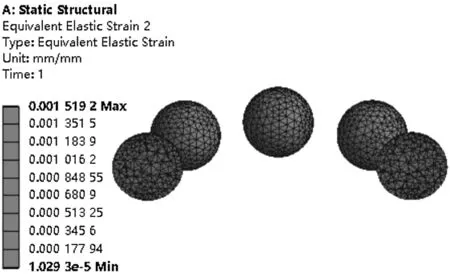
(c)第一級軸承單元滾動體等效應變云圖
由圖7可知:(1)四級軸承組最大等效應力為566.18 MPa,主要集中在第一級碟簧對間的接觸區域;(2)第一級軸承單元等效應力最大值為188.84 MPa,集中在滾動體與滾道面接觸區域;同理,第二、三、四級軸承單元等效應力最大值分別為181.41 MPa、183 MPa、172.72 MPa;(3)第一級軸承單元最大等效應變為0.001 519 2,集中在滾動體與滾道面接觸區域;同理,第二、三、四級軸承單元最大等效應變分別為0.001 457 1、0.001 396 5、0.001 339。
3.2.4 五級軸承組仿真及結果分析
五級軸承組的仿真分析結果如圖8所示。
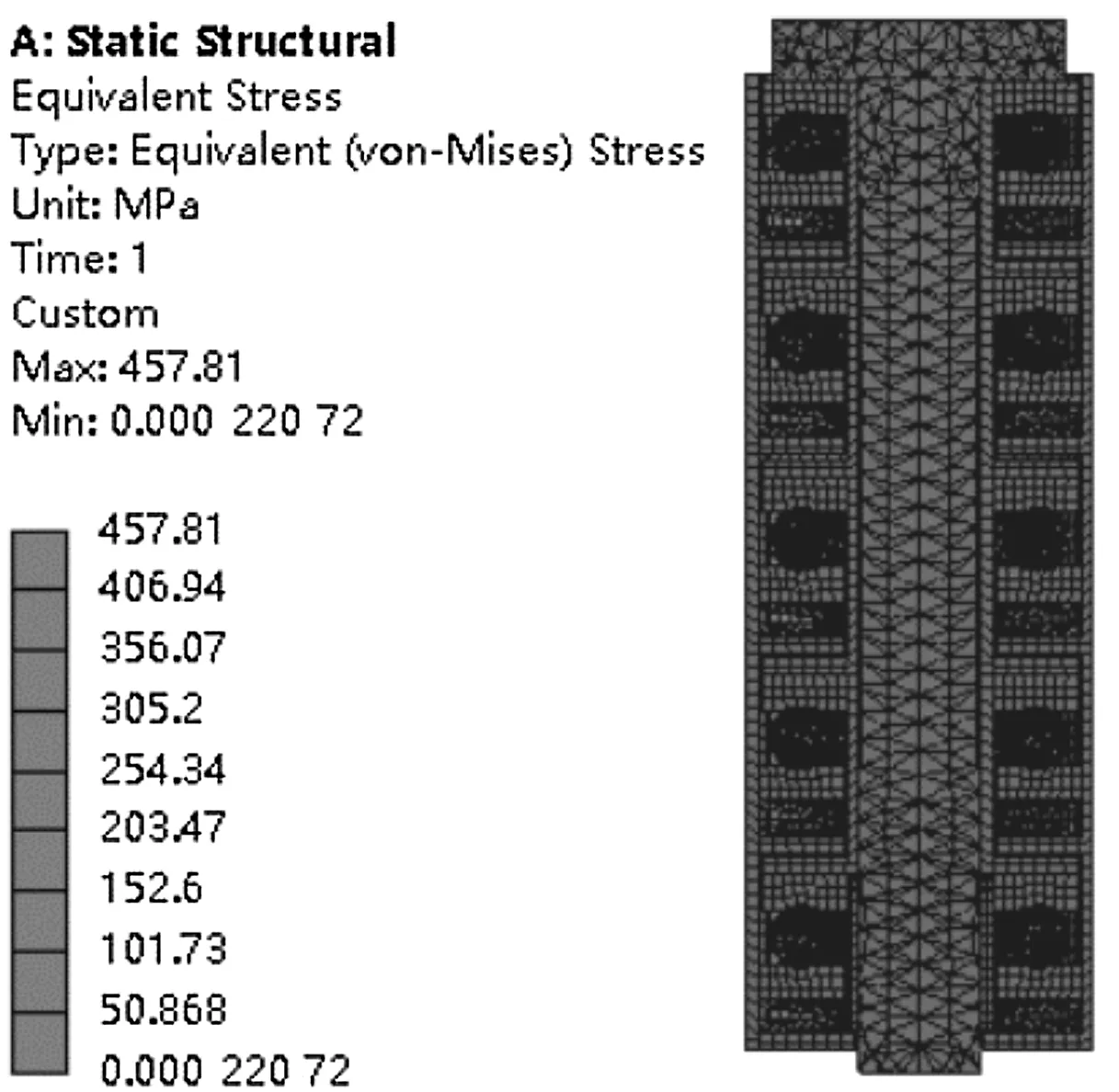
(a)五級軸承組等效應力云圖

(b)第一級軸承單元滾動體等效應力云圖
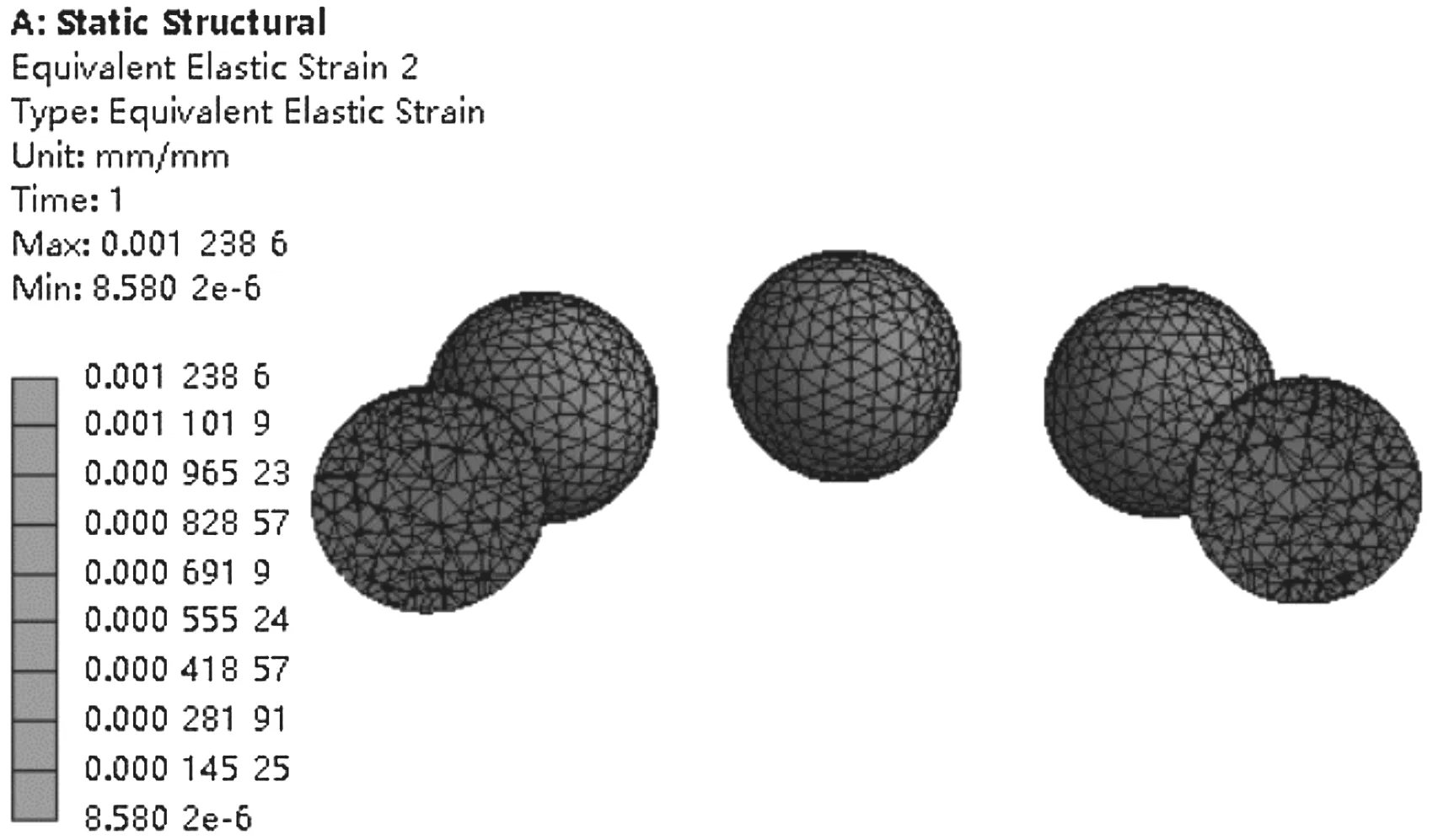
(c)第一級軸承單元滾動體等效應變云圖
由圖8可知:(1)五級軸承組最大等效應力值為457.81 MPa,主要集中在第一級碟簧對間的接觸區域;(2)第一級軸承單元最大等效應力為168.22 MPa;同理,第二、三、四、五級軸承單元最大等效應力分別為159.61 MPa、154.78 MPa、153.22 MPa、141.55 MPa,均集中在滾動體與滾道面接觸區域;(3)第一級軸承單元最大等效應變為0.001 238 6;同理,第二、三、四、五級軸承單元最大等效應變分別為0.001 169、0.001 174 9、0.001 138 2、0.001 030 4,均集中在滾動體與滾道面接觸區域。
4 軸承組均載效果及總體承載能力
綜合上述仿真數據可知,隨著軸承組級數的增加,軸承組最大等效應力、軸承單元等效應力、應變均呈遞減趨勢,各級碟形彈簧變形均勻。因此,筆者主要以等效應力為依據來表征軸承組的均載效果及承載能力。
4.1 軸承組均載效果
為了便于對比分析,筆者將多級軸承組軸承單元等效應力仿真數據制作成表,如表3所示。
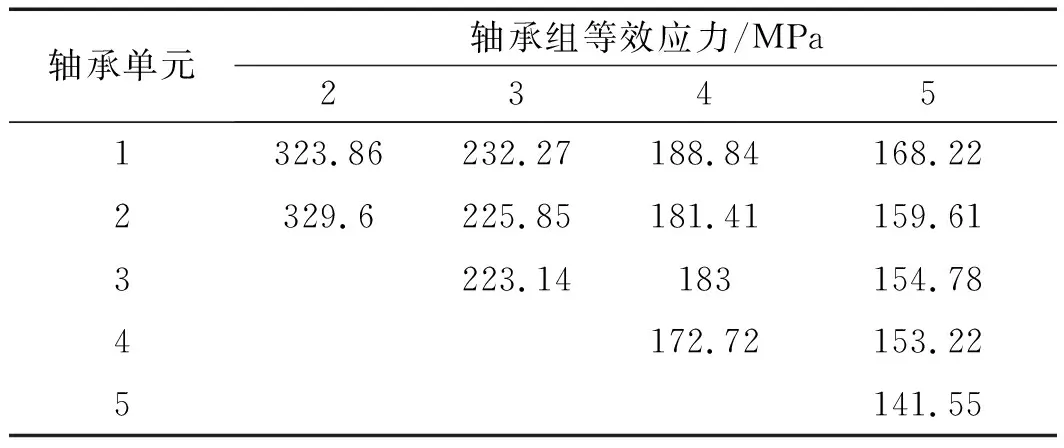
表3 多級軸承組軸承單元等效應力
為了更好地表征軸承組的均載性能,筆者引入量化評價參數—均載率[20]。均載率是用于表征軸向載荷在各級軸承單元間分配均勻程度的指標,其定義為:
(8)
(9)
式中:η—均載率,%;δmax,δmin—施加在軸承單元上的最大等效應力、最小等效應力,MPa;δm—算數平均等效應力,MPa;δa—軸承組各級軸承單元總等效應力,MPa;Z—軸承組級數。
筆者利用公式(8,9)計算所得的均載率數值制作成表,并繪制成點線圖,如圖9所示。
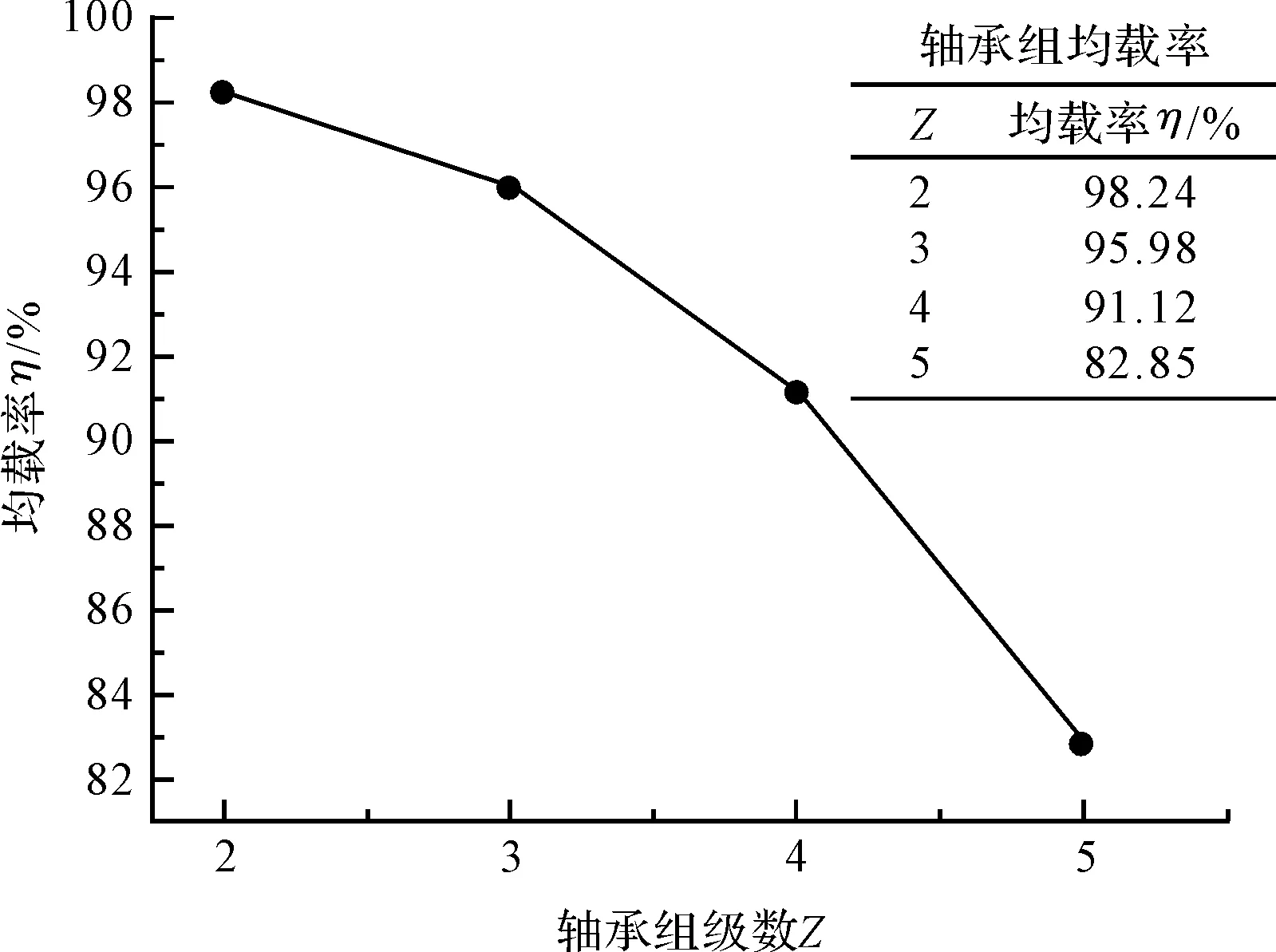
圖9 軸承組均載率
從圖9可見:軸承組均載率達到82%以上,均載效果良好,有效避免了個別軸承單元過載現象的發生,充分提高了軸承單元的承載能力及效率。
但隨著軸承組級數的增加,軸承組均載效果逐漸降低,這是由于選取的碟形彈簧是在標準的基礎上設計的非標支撐,從而導致配套的內套筒軸向尺寸精度過高,而軟件自身的精度有限,致使軸承組在裝配時元件間不可避免地存在微量軸向間隙,如圖10所示(僅為其中一種可能性)。

圖10 元件間的軸向間隙
由圖10可見:元件間存在的微量軸向間隙使得各級碟形彈簧無法同時承載,必然導致各級軸承單元受力不均,即便碟形彈簧的軸向剛度滿足均載的配比要求,實際傳力也會發生變化;此外,若碟簧外圓面與外套筒內圓面存在較大摩擦力,也會改變系統的力平衡關系,導致軸承組的均載效果隨著軸承組級數的增加而進一步降低。
4.2 軸承組總體承載能力
為了便于對比分析,筆者將軸承組最大等效應力值數據制作成表,并繪制成點線圖,如圖11所示。
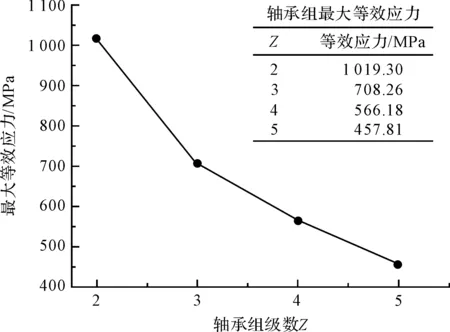
圖11 軸承組最大等效應力
由圖11可見:隨著軸承組級數的增加,軸承組最大等效應力呈遞減趨勢;可見軸承組由于碟簧對間應力集中隨軸承組級數的增加而減弱,直至忽略不計。
為便于對比分析,筆者將多級軸承組軸承單元最大等效應力值制作成表,并繪制成點線圖,如圖12所示。
從圖12中可預測的是,在軸向尺寸允許的情況下,理論上軸承單元最大等效應力值會隨著軸承組級數的增加,一直呈遞減趨勢。
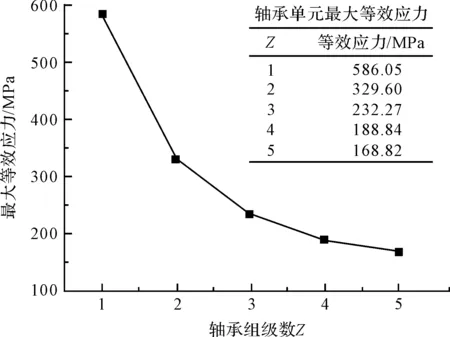
圖12 軸承單元最大等效應力
在軸向載荷一定的情況下,筆者將多級軸承組對原結構等效應力的減少比例,及與上一級減少比例制作成表,如表4所示。
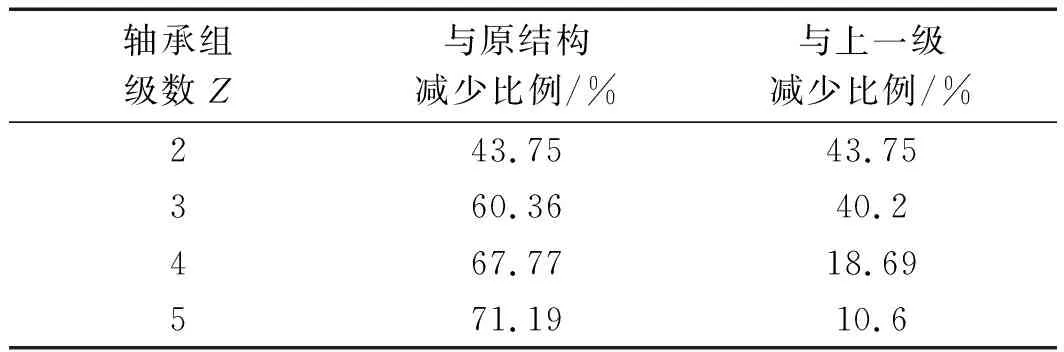
表4 軸承組等效應力減小比例
從表4中可見:二級、三級、四級、五級軸承組對原結構等效應力的減少比例分別為40.75%、60.36%、67.77%、71.19%;同時,三級軸承組等效應力較二級軸承組減少了40.2%,四級軸承組等效應力較三級軸承組減少了18.69%,五級軸承組等效應力較四級軸承組減少了10.6%。由此可見,軸承組可以有效地提高了軸承的承載能力。
筆者將多級軸承組的等效應力減小比例數據繪制成圖,如圖13所示。
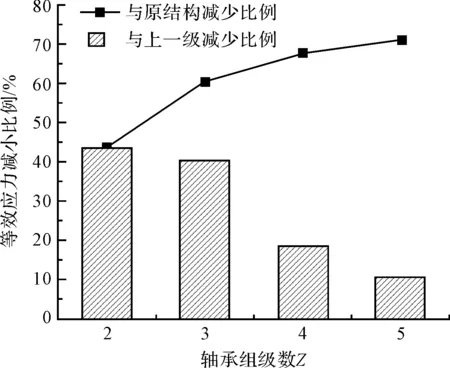
圖13 多級軸承組等效應力減小比例
從圖13可見:軸承組的優化效果與軸承組級數是成正比的,但軸承組的優化程度隨軸承組級數的增加而降低,即軸承組級數超出一定范圍,其優化效果可忽略不計。
因此,在軸承組投入使用前,需根據實際工況選取合適的軸承組級數,以追求效益的最大化。
5 結束語
為解決限徑軸承軸向力過大導致系統整體壽命受限這一關鍵技術難題,筆者設計了串行軸承組結構,旨在使軸承組軸承單元平均承擔軸向載荷以求提高系統整體壽命;應用數值仿真方法對比分析了軸承組與原結構的應力、應變特征。
研究結論如下:
(1)串行軸承組實現了對軸向載荷的均載效應,突破了徑向尺寸的限制,成功解決了限徑軸承因軸向載荷過大導致壽命過短的問題;
(2)軸承組均載率在82%以上,均載效果良好,各級軸承單元碟簧變形量小且均勻,有效提高了軸承組件的承載能力;
(3)軸承組額定動載荷大,軸承組級數對原結構的優化效果是成正比的,即在軸向載荷一定的情況下,二級、三級、四級、五級軸承組對原結構等效應力的減少比例分別為40.75%、60.36%、67.77%、71.19%,有效減少了軸承單元的軸向載荷。
因為串行軸承組的承載能力及均載性能仍有待提高,所以在下一步的研究中,筆者將著手對軸承組的各組成元件進行優化設計,以求提高軸承組的承載能力及均載性能,同時進行必要的實驗分析。

