綜合高低頻段分量的諧振接地系統故障選線

徐 耀，田 書，楊淇翔

（河南理工大學電氣工程與自動化學院，焦作 454003）

諧振接地系統發生單相接地故障時，由于消弧線圈的存在使得故障電流更加微弱，加之暫態過程持續時間短，選線結果很容易受故障條件的影響，尤其當故障發生在相電壓過零點附近時，選線的準確性進一步受到影響[1-3]。

鑒于故障后暫態電流幅值高、能量大，故障信息豐富，目前基于暫態分量的選線法受到普遍關注[4]，多種基于暫態分量的選線方法被提出，包括小波分析法[5-7]、S 變換法[8]、波形比較法[9-11]、注入信號法[12]等。這些基于暫態信號的選線方法大多利用零序電流高頻暫態分量進行選線，但在小故障合閘角、大故障電阻等其他復雜情況下，高頻分量易受到干擾，選線準確性也會受到影響。文獻[7]通過比較零序電流在高、低頻段能量的大小，選取能量較大頻段的故障信息進行選線。文獻[8]利用S變換提取得到在特征頻帶中的暫態信號的極性和能量特性進行選線。文獻[9-11]提出基于暫態零序電流波形相似度的選線法，但原理上只利用了故障信號的高頻分量，忽略了衰減直流分量的影響，在小故障合閘角等惡劣情況下的選線準確性受到影響。

隨著HHT算法[13-14]的提出，經驗模態分解EMD（empirical mode decomposition）被廣泛用于故障選線之中[15-16]。文獻[15]通過對系統各出線的零序導納進行EMD分解，利用故障線路和健全線路之間特征量的符號差異構成選線判據。文獻[16]通過對故障零序電流進行EMD分解并提取出第一個模態分量的5次諧波，而后利用Duffing振子反映系統相位圖的變化以判斷線路是否發生故障。但由于EMD在分解過程中易受噪聲影響而發生模態混疊，且其分解效果不太直觀，因此在一些惡劣故障條件下，EMD算法難以確保故障信號的提取精度，從而可能造成選線誤判。而相較于EMD算法，VMD（variational mode decomposition）算法對故障暫態零序電流的重構更加直觀及穩定，同時可以有效避免模態混疊。

為了充分利用故障信號的故障信息，提出一種基于Hilbert邊際譜能量熵和曲線斜率的諧振接地系統故障選線方法。首先通過果蠅算法優化VMD中K、α值的參數設置，利用優化后的VMD對各饋線零序電流及母線零序電壓進行分解，得到頻率由低到高的K個本征模態函數IMF（intrinsic mode function），進而提取出其高、低頻分量相應的故障特征，以Hilbert邊際譜能量熵值大小反映各饋線低頻段衰減直流分量含量的差異，以曲線斜率反映各饋線高頻段零序電流與零母線序電壓導數的線性關系。最終構成Hilbert邊際譜能量熵和曲線斜率極性的雙重判據選線方法。

1 零序網絡故障暫態特征

當諧振接地系統發生單相接地故障時，其等值零序回路如圖1所示。其中：L0、R0分別為零序等效對地電感和電阻；C0為系統對地零序電容總和；LP為消弧線圈等效電感；RP為消弧線圈等效電阻；um為故障相電壓Uf0的幅值。

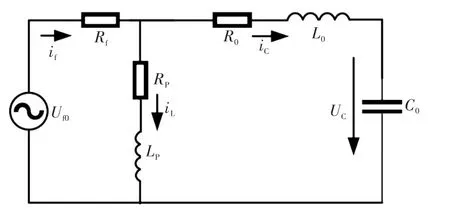
圖1 零序網絡等效電路Fig.1 Equivalent circuit of zero-sequence network

根據圖1列寫KVL方程為

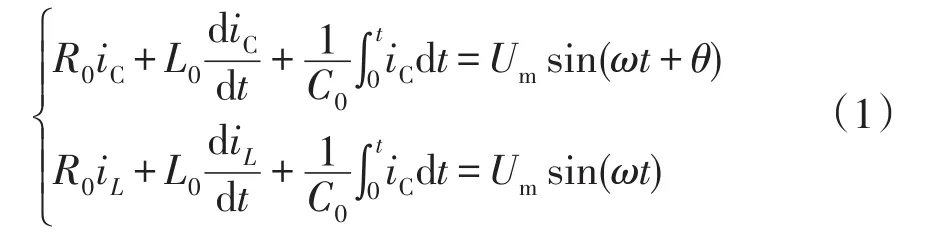
求解式（1）可得出故障電流為

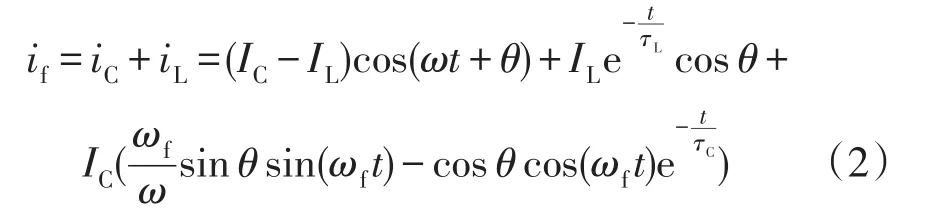
式中：iC、iL分別為暫態電容電流和電感電流；IC、IL為iC、iL的幅值；τL、τC為電感、電容時間常數；ω為角頻率；ωf為暫態振蕩角頻率；t為時間；θ為零序電壓初始相位角，即故障合閘角。

式（2）中第一項為故障電流的穩態分量，其余為故障電流的暫態分量。其中暫態分量分別為低頻段電感電流的衰減直流分量和高頻段暫態電容電流分量。當故障發生在相電壓峰值處，即θ=90°時，高幅值的暫態高頻電容電流分量占主要成分，衰減直流分量占比很小幾乎為0；而當故障發生在相電壓過零處，即θ=0°時，衰減直流分量占主要成分，暫態高頻電容電流占比很小。由此可見，不同故障時刻下，故障線路和健全線路的零序電流在低頻段有著不同含量的衰減直流分量，在高頻段有著不同的幅值和相位特性。

2 基于參數優化VMD的信號特征提取

在實際電力系統中，配電網各出線的類型、長度不同導致其具有不同的相頻特性，并且不同的故障情況也會造成不同故障線路暫態主頻段的不匹配。因此，傳統的低通、帶通濾波器可能會導致故障分量提取不精確。本文利用參數優化后的VMD對各饋線進行分解，能有效提高故障特征提取的精度。

2.1 VMD原理

VMD分解其本質是將原始輸入信號分解為K個具有中心頻率且頻率從低到高的有限帶寬信號，即固有模態分量IMF[17-18]。相應的變分模型為

2.2 參數優化VMD的信號分解

然而VMD算法仍存在的一個問題就是：分解層數K和懲罰因子α的值需要預先人為設定[19]。而參數值設置的不同，最終的分解效果也將不同。鑒于單相接地故障情況隨機且復雜，在分解信號前，要預先選取合適的K和α值以達到最佳的分解效果。

果蠅優化算法是一種全局搜索能力很強的智能優化算法，相比粒子群算法和遺傳算法等優化算法，其尋優速度快、計算量小、所需確定的參數少，算法使用難度低[20-21]。包絡熵[22]能夠反映信號稀疏特性，本文以包絡熵為適應度函數，利用果蠅算法優化VMD的K、α值，篩選出最佳的參數組合。

VMD算法參數K和α的優化過程如下：

（1）初始化果蠅群體的位置為參數組合[K，α]；

（2）在不同濃度位置[K，α]處對故障電流信號做VMD分解，計算各個模態分量IMF的包絡熵值并取最小包絡熵值為局部極小熵值；

（3）比較局部極小熵值的大小，尋找全局極小熵值；

（4）果蠅群體是否達到了最優的位置，與上一代相比是否優于下一代；

（5）若步驟（4）未完成，則轉至步驟（2），直到尋優次數達到設定值后，輸出最佳適應度值及果蠅位置。

2.3 信號分解測試

以4.1節模型為例，取線路L1在距母線5 km處發生單相接地故障，過渡電阻為5 Ω，故障合閘角為90°，利用優化后的VMD對各出線零序電流及母線零序電壓進行分解，當果蠅進化到第5代時得到局部極小熵值5.234，如圖2所示。此時得到的優化參數值為K=5、α=1 973。

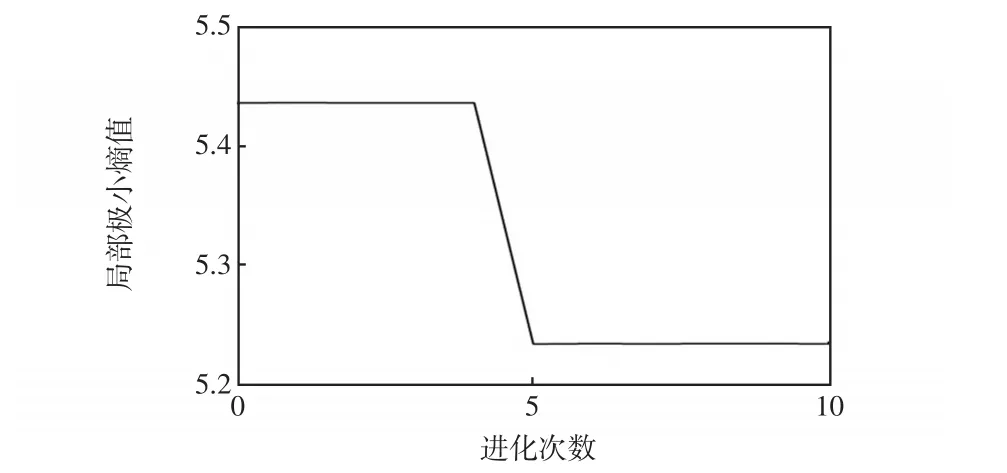
圖2 局部極小熵值隨進化次數的變化Fig.2 Changes in local minimum entropy with the number of evolutions

故障線路零序電流分解結果如圖3（a）所示，對各個IMF分量做快速傅里葉變換得到其頻譜圖如圖 3（b）所示。通過圖 3（b）可以看出，低頻分量IMF1的瞬時頻率在50 Hz左右，高頻分量IMF5的瞬時頻率在1 300 Hz左右，基本符合故障零序電流的頻段分布。據此以IMF1表征低頻衰減直流分量，以IMF5表征暫態高頻電容分量，進行后續選線判據分析。

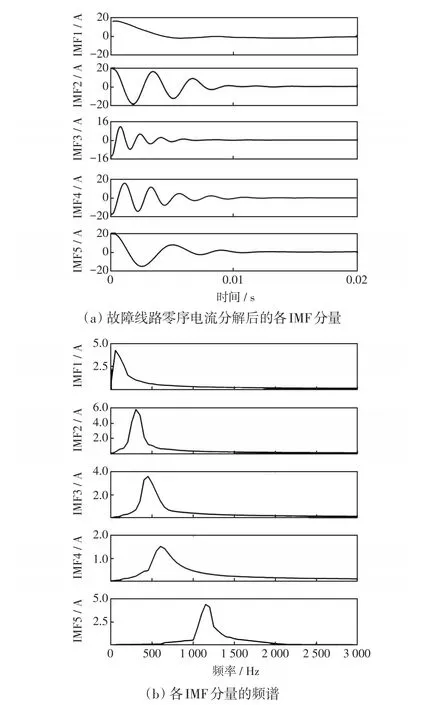
圖3 參數優化VMD分解得的各IMF分量和各IMF的頻譜Fig.3 IMF components decomposed by parameter optimized VMD，and the spectrum of each IMF

3 選線判據及理論分析

當故障發生后，不論故障合閘角的大小如何，非故障線路的低頻分量中均不包含衰減直流分量；并且故障線路和健全線路的零序電流與母線零序電壓導數之間呈現不同的線性關系[23]。通過計算各線路低頻段衰減直流分量的Hilbert邊際譜能量熵實現初步選線判定，進而比較各線路高頻段零序電流與母線零序電壓導數曲線斜率的極性，可實現綜合高、低頻段故障信息的雙重判據選線。

3.1 Hilbert邊際譜能量熵

Hilbert邊際譜具有較高的分辨率，可以精確地描述信號幅值在整個頻段上隨時間和頻率的變化規律[24]，而熵可以反映信號的混亂程度。因此，通過計算各饋線IMF1分量的Hilbert邊際譜能量熵，可以反映故障線路和健全線路間低頻段衰減直流分量含量的差異。具體分析過程參見文獻[24]。

通過對各饋線IMF1分量進行Hilbert轉換并求其積分得到Hilbert邊際譜hi(f)，則邊際譜能量表達式為

根據信息熵的基本理論，定義Hilbert邊際譜能量熵為

對各線路熵值進行歸一化處理，得到最終的Hilbert邊際譜能量熵表達式為

式中：hi(ω)、Ei分別為各線路IMF1分量的Hilbert邊際譜、Hilbert邊際譜能量；Hi為各線路IMF1分量的Hilbert邊際譜能量熵。

3.2 曲線斜率分析

由圖4等效零序網絡可知，對于一個包含n條出線的系統，當線路1發生單相接地故障時，健全線路零序電流與母線零序電壓導數的關系式為

圖4 等效零序網絡Fig.4 Equivalent zero-sequence network

故障線路零序電流與母線零序電壓導數的關系式為

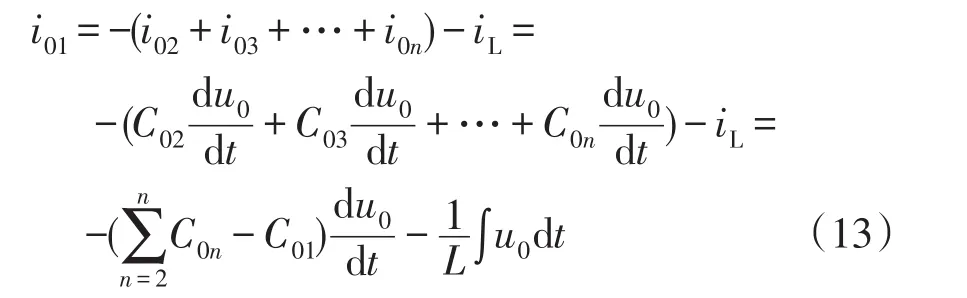
由式（12）、（13）可知，健全線路和故障線路的零序電流與母線零序電壓導數之間具有不同的線性特性，通過對各饋線零序電流高頻分量與母線零序電壓進行最小二乘法線性擬合并求其曲線斜率Ki，得到各饋線高頻分量相應的斜率極性。

3.3 選線流程

（1）在線監測系統母線零序電壓U0的有效值，當大于整定值KNUN（一般為母線額定電壓UN的0.15～0.3倍，本文取KN=0.3）時，判定系統發生接地故障，啟動選線保護裝置；

（2）利用參數優化后的VMD算法提取出各線路零序電流及母線零序電壓的高、低頻分量；

（3）對分解得到的各饋線低頻分量進行Hilbert邊際譜能量熵計算；對各饋線零序電流高頻分量與母線零序電壓導數進行線性分析及曲線斜率計算。

通過大量仿真結果驗證，設定能量熵閾值Hset=Himax/Hjsec>1，當各出線能量熵值中最大熵值與次最大熵值比值大于1時，初步判定能量熵值最大的線路為故障線路；當比值小于1時，轉而計算各出線高頻分量曲線斜率，若所有饋線的曲線斜率均為正值，判定發生母線故障；當曲線斜率存在唯一斜率為負時，判定該線路為故障線路。

選線的流程如圖5所示。

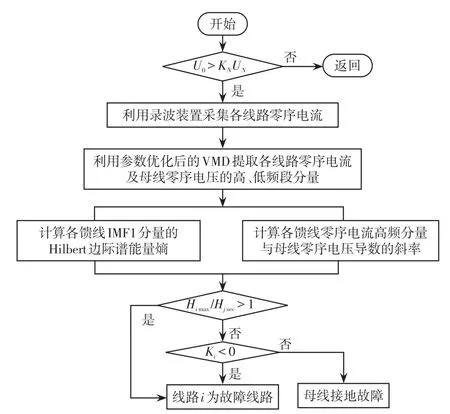
圖5 選線流程Fig.5 Flow chart of feeder detection

4 仿真分析

4.1 仿真模型

利用Matlab/Simulink建立10 kV諧振接地系統，系統簡化圖及線路類型及參數如圖6所示，線路參數[25]如表1所示。消弧線圈過補償度為8%，其等效電感LP=(1/1.08)×(1/3ω2C0)=0.756 H ，有功損耗取感性損耗的3%即RP=0.03ωL=7.124 Ω。考慮到故障暫態信號的高頻分量大致為300～3 000 Hz，并且暫態過程持續時間短，因此，仿真設定本系統的采樣頻率為10 kHz，仿真時間窗為故障發生后的1個工頻周期共200個采樣點。

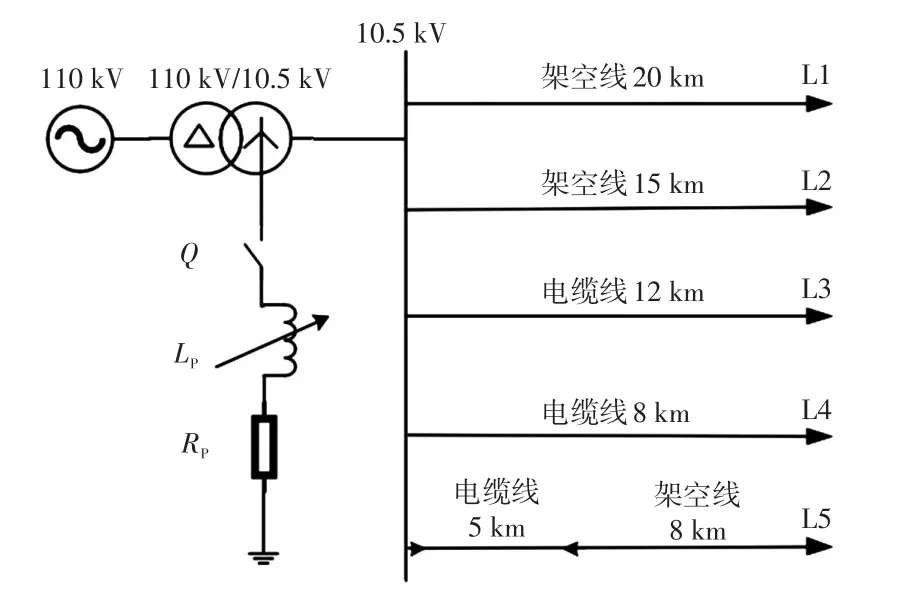
圖6 10 kV諧振接地系統簡化圖Fig.6 Simplified diagram of 10 kV resonant grounding system

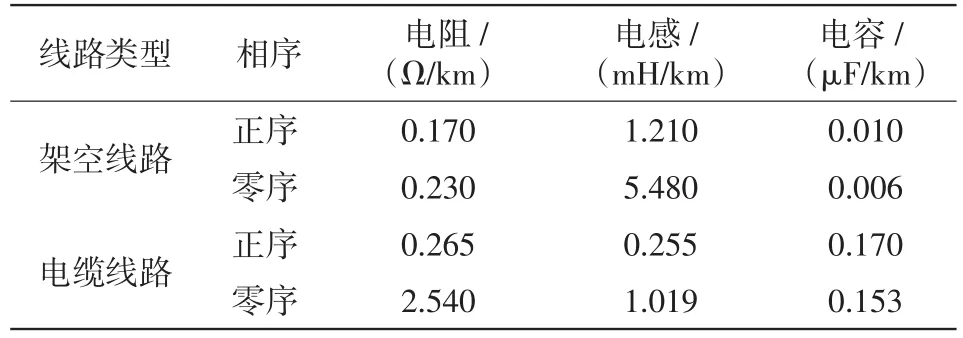
表1 線路參數Tab.1 Line parameters

4.2 仿真實驗

1）故障分析

仿真實驗將從不同故障線路Lm的不同故障位置Xf(km)、不同故障電阻Rf(Ω)、不同故障時刻θ(°)、算法適應性及與其他方法對比這幾個方面驗證該方法的有效性。限于篇幅，本文僅給出3種故障情況的具體過程分析。

故障1：取線路L1在距離母線Xf=3 km處發生單相接地故障，故障電阻Rf=50 Ω，故障合閘角θ=90°。利用果蠅優化算法優化VMD分解中[K，α]的選取，經過迭代計算，當果蠅進化到第3代時得到局部極小熵值3.231，此時所對應的[K，α]為[3，1 673]，據此選取IMF1分量作為低頻段衰減直流分量，IMF3為高頻暫態電容分量進行故障特征計算分析。由于故障發生在相電壓峰值處，此時故障線路L1低頻段含有少量衰減直流分量的零序電流，計算各出線零序電流低頻分量Hilbert邊際譜能量熵可得，最大能量熵出線L1與次最大能量熵出線L3的比值為Himax/Hjsec=0.434/0.297=1.461>1，初步判斷線路L1為故障線路；對高頻段零序電流與母線零序電壓導數進行線性擬合，結合各饋線曲線斜率可最終判定故障線路為出線L1。電流-電壓導數曲線如圖7所示，結果如表2所示。

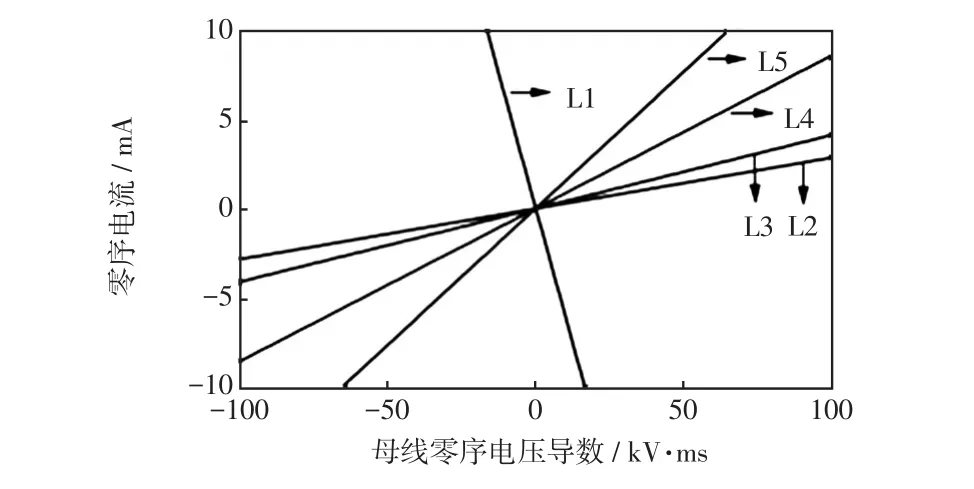
圖7 故障1各出線的線性擬合曲線Fig.7 Linear fitting curve of each feeder under fault 1

表2 故障1的選線結果Tab.2 Feeder detection results under fault 1

故障2：取線路L3在距離母線Xf=6 km處發生單相接地故障，故障電阻Rf=100 Ω，故障合閘角θ=0°。經過優化，當果蠅進化到第3代時得到局部極小熵值3.978，此時對應的參數組合[K，α]為[3，2 046]，據此選取IMF1分量作為低頻段衰減直流分量，IMF3為高頻暫態電容分量進行故障特征計算分析。由于故障發生在相電壓過零點處，故障線路L3的零序電流中含有大量低頻段衰減直流分量，通過計算各出線零序電流低頻分量Hilbert邊際譜能量熵可得，最大能量熵出線L3與次最大能量熵出線L4的比值為Himax/Hjsec=0.633/0.164=3.859>1，可初步判斷線路L3為故障線路；對高頻段零序電流與母線零序電壓導數進行線性擬合，結合各饋線曲線斜率極性可最終判定故障發生在線路L3上。電流-電壓導數曲線如圖8所示，結果如表3所示。

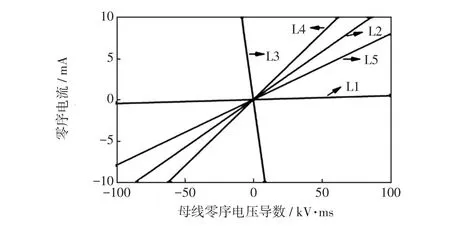
圖8 故障2各出線的線性擬合曲線Fig.8 Linear fitting curve of each feeder under fault 2

表3 故障2的選線結果Tab.3 Feeder detection results under fault 2

故障3：取線路L5在線-纜結點處發生單相接地故障，故障電阻Rf=500 Ω，故障合閘角θ=45°。此時當果蠅進化到第5代時得到局部極小熵值3.411，對應的[K，α]為[K=5，α=1 437]，據此選取IMF1分量作為低頻段衰減直流分量，IMF5為高頻暫態電容分量進行故障特征計算分析。計算所得的最大能量熵出線L5與次最大能量熵出線L3的比值為Himax/Hjsec=0.596/0.195=3.056>1，結合零序電流-電壓導數曲線斜率極性可最終判定線路L5為故障線路。電流-電壓導數擬合曲線如圖9所示，結果如表4所示。

圖9 故障3各出線的線性擬合曲線及其放大圖Fig.9 Linear fitting curve of each feeder under fault 3

表4 故障3的選線結果Tab.4 Feeder detection results under fault 3

2）算法適應性

由于配電網現場環境的復雜，故障情況多變，且不可避免的受到噪聲的影響，仿真通過加入信噪比為50 dB的高斯白噪聲，來測試本方法在不同故障距離、故障電阻、故障合閘角等故障情況下的選線的準確性。具體仿真結果如表5所示。

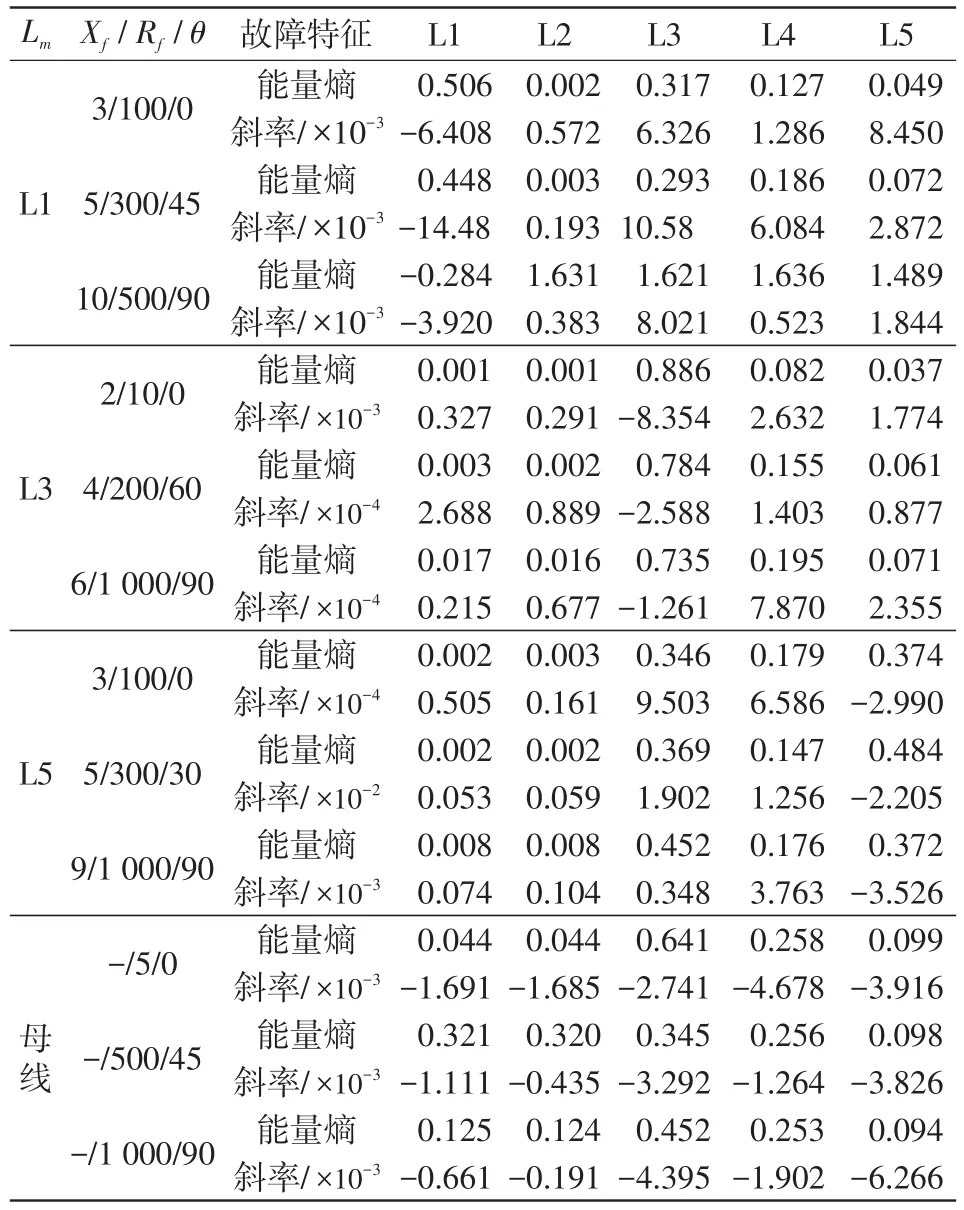
表5 故障選線結果Tab.5 Results of fault feeder detection

3）間歇性電弧故障

當故障電流的幅值超過一定值時，過程復雜的間歇性電弧時常發生。仿真設定故障線路為出線L1，故障點距母線8 km，故障電阻為Rf=200 Ω，故障合閘角為θ=30°，利用Mayr電弧模型測試本文方法在電弧周期為Tarc=0.002 s時間歇性電弧接地故障的選線效果。此時經果蠅算法優化所得的VMD參數組合為[K=4，α=1 865]，綜合計算所得的Hilbert邊際譜能量熵及曲線斜率結果可以看出，本方法在發生間歇性電弧故障時依然能夠準確篩選出故障線路。電流-電壓導數曲線斜率如圖10所示，仿真結果如表6所示。

表6 間歇性電弧接地故障的選線結果Tab.6 Feeder detection results under intermittent arc grounding fault

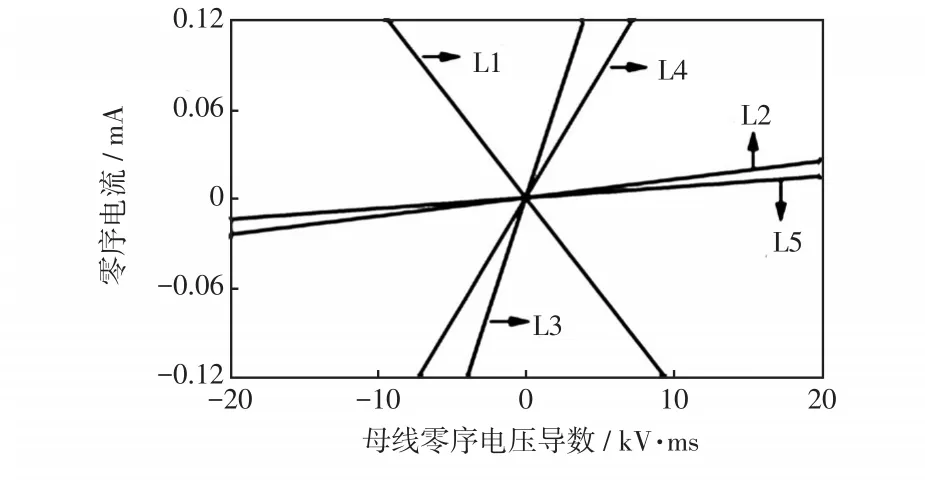
圖10 各出線的線性擬合曲線Fig.10 Linear fitting curve of each feeder

4）不同消弧線圈過補償度P

在諧振接地系統中，消弧線圈的過補償效應會進一步削減故障線路零序電流的幅值，并且削減的幅度與消弧線圈過補償度P的大小有關。取故障發生在線路L3距母線5 km處，故障合閘角θ=0°，故障電阻Rf=50 Ω，測試本文方法在不同消弧線圈補償度P下的選線準確性，表7仿真結果驗證了本文方法適用于不同消弧線圈過補償度P下的故障情況。

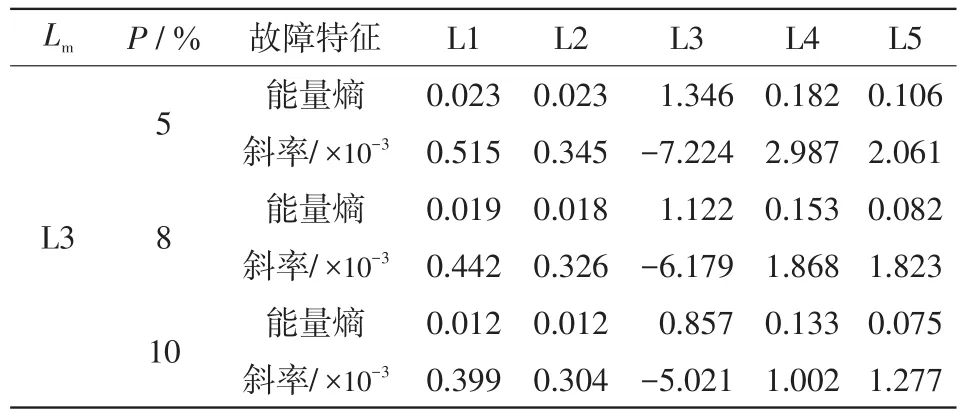
表7 不同過補償度下的選線結果Tab.7 Feeder detection results under different compensation degrees

5）與其他方法對比

小波變換WT（wavelet transform）和EMD是目前得到廣泛應用的選線方法，本節設置小波基函數為db10，分解層數為6層，分別利用各饋線零序電流高頻段（300～3 000 Hz）內的小波能量和模態函數的相關系數（correlation coefficient）作為故障特征構造選線判據，仿真通過加入信噪比為50 dB的高斯白噪聲來測試兩種方法在不同故障條件下的選線結果，并與本文方法作對比，結果如表8所示。

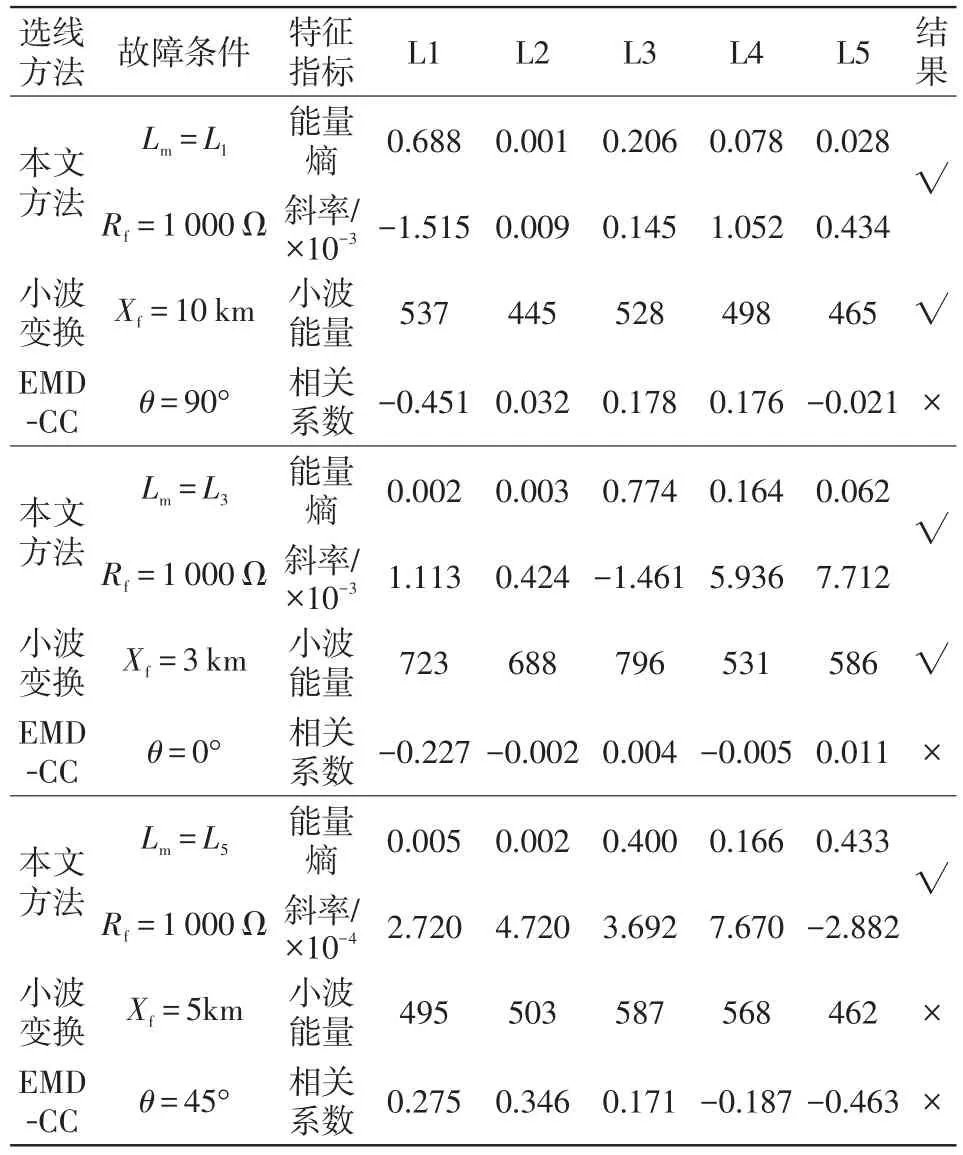
表8 與其他方法對比Tab.8 Comparison with other methods

小波能量法雖然能篩選出故障線路，但各饋線間故障特征指標的區分度較小，從而可能會導致選線誤判；而傳統EMD分解結合相關系數的方法由于噪聲干擾而出現模態混疊現象，無法做出正確判斷。據此，在小故障合閘角的高阻故障等惡劣故障條件下，兩種方法的選線準確性均受到考驗。而本文方法綜合高、低頻段故障分量，結合衰減直流分量的幅值及高頻暫態分量的極性，能夠確保在不同故障情況下故障信號的準確提取，具有良好的自適應性及穩定性。

5 結論

本文通過分析諧振接地系統發生單相接地故障時的故障零序電流成分，利用故障線路和健全線路的零序電流在高、低頻段具有不同的故障特征這一特性，提出一種基于Hilbert邊際譜能量熵和曲線斜率的選線方法。結論如下：

（1）本文方法同時考慮到衰減直流分量的含量差異及電流-電壓導數曲線斜率的互異，充分利用了高、低頻段故障信息，具有良好的自適應性；

（2）由于VMD分解相對于EMD分解能有效避免模態混疊，該方法對噪聲干擾和間歇性接地故障也有著一定的魯棒性；

（3）大量仿真驗證該方法不受故障電阻、位置、合閘角及噪聲干擾等因素的影響，同時能有效區分出線故障和母線故障；

（4）該方法所需采樣點數少，上傳數據量小，計算速度快，能減輕通信裝置的負擔。