基于Bagging的雙向GRU集成神經(jīng)網(wǎng)絡(luò)短期負(fù)荷預(yù)測

王 康，張智晟，撖奧洋，于立濤

（1.青島大學(xué)電氣工程學(xué)院，青島 266071；2.國網(wǎng)青島供電公司，青島 266002）

由于目前的技術(shù)還無法實(shí)現(xiàn)電能的大量存儲(chǔ)，要想保證電力系統(tǒng)的安全穩(wěn)定運(yùn)行，提高經(jīng)濟(jì)效益，就需要對(duì)電力負(fù)荷進(jìn)行預(yù)測。電力系統(tǒng)短期負(fù)荷預(yù)測主要是根據(jù)歷史電力負(fù)荷、天氣溫度、日期類型等因素對(duì)未來幾個(gè)小時(shí)至幾天的電力負(fù)荷進(jìn)行預(yù)估[1]。高精度的短期負(fù)荷預(yù)測對(duì)實(shí)現(xiàn)電力系統(tǒng)的供求平衡、減少資源浪費(fèi)具有重要的指導(dǎo)意義[2]，并直接影響電力系統(tǒng)后續(xù)的經(jīng)濟(jì)調(diào)度等工作，短期負(fù)荷預(yù)測已經(jīng)成為提高電力系統(tǒng)發(fā)電設(shè)備利用率和經(jīng)濟(jì)調(diào)度效率的重要環(huán)節(jié)。

電力負(fù)荷受天氣溫度、日期類型等多種因素的影響，使得負(fù)荷預(yù)測的難度增大。目前應(yīng)用較多的短期負(fù)荷預(yù)測方法主要有傳統(tǒng)統(tǒng)計(jì)學(xué)方法和機(jī)器學(xué)習(xí)方法兩類。統(tǒng)計(jì)學(xué)方法主要有卡爾曼濾波法[3]、指數(shù)平滑法[4]等，這些方法計(jì)算簡單，但是對(duì)原始序列的要求較高，使得預(yù)測精度有所下降且預(yù)測穩(wěn)定性較差。機(jī)器學(xué)習(xí)方法主要有支持向量機(jī)SVM（support vector machine）[5]和人工神經(jīng)網(wǎng)絡(luò)ANN（artificial neural network）[6]等。SVM方法較好地解決了預(yù)測過程中容易出現(xiàn)的局部最優(yōu)解的問題，但是參數(shù)選取較為復(fù)雜，收斂速度慢。ANN方法因其運(yùn)算速度快、預(yù)測精度高的特點(diǎn)得到了廣泛應(yīng)用。在ANN中，反向傳播BP（back propagation）神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)簡單，計(jì)算速度較快，但BP神經(jīng)網(wǎng)絡(luò)容易陷入局部最優(yōu)解，預(yù)測精度較低[7]。文獻(xiàn)[8]提出了一種基于CNN-LSTM混合神經(jīng)網(wǎng)絡(luò)模型的短期負(fù)荷預(yù)測方法，將卷積神經(jīng)網(wǎng)絡(luò)CNN（convolu?tional neural network）與長短期記憶LSTM（long short-term memory）網(wǎng)絡(luò)進(jìn)行結(jié)合，利用了CNN能夠有效提取特征向量和LSTM網(wǎng)絡(luò)訓(xùn)練過程中不會(huì)出現(xiàn)梯度問題的特點(diǎn)，但是3個(gè)門控循環(huán)單元的引入使得LSTM網(wǎng)絡(luò)訓(xùn)練速度有所下降。文獻(xiàn)[9]提出了一種基于GRU的深度學(xué)習(xí)網(wǎng)絡(luò)短期負(fù)荷預(yù)測模型，將門控循環(huán)單元GRU（gated recurrent unit）神經(jīng)網(wǎng)絡(luò)和深度神經(jīng)網(wǎng)絡(luò)相結(jié)合，達(dá)到了提高預(yù)測精度的效果，但是單向GRU神經(jīng)網(wǎng)絡(luò)在預(yù)測過程中無法考慮未來時(shí)刻的負(fù)荷信息。文獻(xiàn)[10]提出了一種基于多層雙向循環(huán)神經(jīng)網(wǎng)絡(luò)的短期負(fù)荷預(yù)測模型，預(yù)測過程中充分考慮了預(yù)測點(diǎn)過去和未來的狀態(tài)信息，但是預(yù)測過程中僅利用人工神經(jīng)網(wǎng)絡(luò)使得模型預(yù)測穩(wěn)定性較差。

為了達(dá)到更好的預(yù)測效果，本文提出了一種基于Bagging算法的雙向加權(quán)GRU集成神經(jīng)網(wǎng)絡(luò)短期負(fù)荷預(yù)測模型，對(duì)雙向門控循環(huán)單元BiGRU（bidi?rectional gated recurrent unit）神經(jīng)網(wǎng)絡(luò)[11]中兩個(gè)方向的隱含層狀態(tài)進(jìn)行加權(quán)求和處理，解決了循環(huán)神經(jīng)網(wǎng)絡(luò)RNN（recurrent neural network）中容易出現(xiàn)的梯度問題[12]，在預(yù)測過程中通過調(diào)節(jié)比例系數(shù)可以改變兩個(gè)方向信息的融合比例，從而使前向信息和反向信息得到更充分的利用[13]。與LSTM網(wǎng)絡(luò)[14]相比，GRU網(wǎng)絡(luò)將門控循環(huán)單元的個(gè)數(shù)從3個(gè)減少到2個(gè)[15]，在一定程度上可以加快訓(xùn)練速度。通過Bagging算法集成雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)，可以進(jìn)一步提高預(yù)測模型的穩(wěn)定性，增強(qiáng)了模型的泛化能力。利用某地區(qū)電網(wǎng)真實(shí)負(fù)荷數(shù)據(jù)進(jìn)行驗(yàn)證可以得出，本文所提模型具有較高的預(yù)測精度。

1 雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)

1.1 GRU神經(jīng)網(wǎng)絡(luò)

RNN在模型中加入了循環(huán)結(jié)構(gòu)，從而可以考慮預(yù)測點(diǎn)上一時(shí)刻的隱含層狀態(tài)，在時(shí)間序列預(yù)測方面應(yīng)用效果較好。傳統(tǒng)的RNN將當(dāng)前時(shí)刻的輸入與上一時(shí)刻隱含層的狀態(tài)共同作為神經(jīng)網(wǎng)絡(luò)的輸入，將RNN按照時(shí)間維度展開的結(jié)構(gòu)如圖1所示。圖1中：xt為當(dāng)前時(shí)刻的輸入值；W為RNN輸入層到隱含層的權(quán)重；Wy為RNN隱含層到輸出層的權(quán)重；ht為當(dāng)前時(shí)刻隱含層狀態(tài)；yt為當(dāng)前時(shí)刻的輸出。

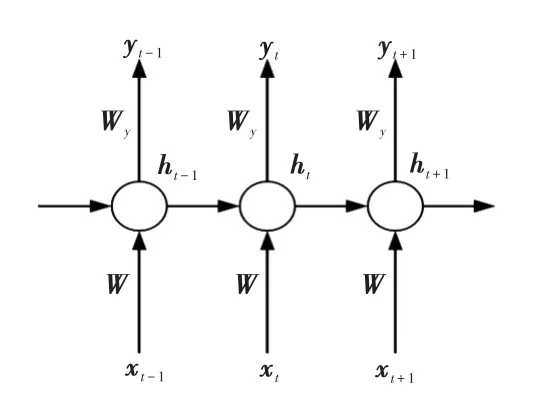
圖1 RNN展開結(jié)構(gòu)Fig.1 Expanded structure of RNN

從圖1可以看出，RNN在預(yù)測時(shí)考慮了歷史時(shí)刻的狀態(tài)對(duì)當(dāng)前時(shí)刻的影響，故能對(duì)時(shí)間序列數(shù)據(jù)進(jìn)行較好的預(yù)測，但是傳統(tǒng)的RNN在預(yù)測長時(shí)間序列時(shí)容易出現(xiàn)梯度消失、梯度爆炸的問題，GRU神經(jīng)網(wǎng)絡(luò)以門控循環(huán)單元代替?zhèn)鹘y(tǒng)的循環(huán)單元來解決RNN中容易出現(xiàn)的梯度問題，與同樣使用門控循環(huán)單元的LSTM神經(jīng)網(wǎng)絡(luò)相比，GRU神經(jīng)網(wǎng)絡(luò)僅需要2個(gè)門控循環(huán)單元即可解決梯度問題[16]，在一定程度上節(jié)省了內(nèi)存，加快了運(yùn)行速度，GRU神經(jīng)網(wǎng)絡(luò)循環(huán)單元的結(jié)構(gòu)如圖2所示。圖2中：ht-1為上一時(shí)刻隱含層狀態(tài)；rt為重置門；zt為更新門；σ為sigmoid激活函數(shù)。

圖2 GRU循環(huán)單元結(jié)構(gòu)Fig.2 Structure of GRU

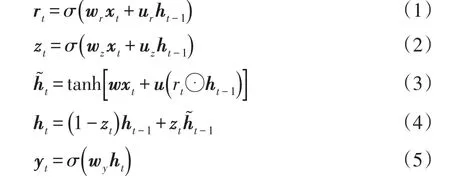
式中：wr、ur、wz、uz、w、u為神經(jīng)網(wǎng)絡(luò)權(quán)值；⊙為不同矩陣的Hadamard積；yt為當(dāng)前時(shí)刻的輸出值。

GRU神經(jīng)網(wǎng)絡(luò)主要通過2個(gè)門對(duì)輸入信息進(jìn)行更新[17]，通過sigmoid函數(shù)將數(shù)據(jù)變換到0～1之間，并結(jié)合乘法操作可以實(shí)現(xiàn)對(duì)輸入信息以及歷史信息的選擇性重置，重置門rt主要影響上一時(shí)刻信息的保留情況，更新門zt主要對(duì)當(dāng)前時(shí)刻隱含層狀態(tài)進(jìn)行更新。與LSTM相比，GRU循環(huán)單元最大的改進(jìn)就是僅通過1個(gè)更新門zt以及1-zt同時(shí)實(shí)現(xiàn)了對(duì)信息的遺忘和保留，從而提高了訓(xùn)練速度。

1.2 雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)

GRU神經(jīng)網(wǎng)絡(luò)與LSTM神經(jīng)網(wǎng)絡(luò)都是對(duì)RNN的改進(jìn)，在保證RNN在時(shí)間序列預(yù)測方面的優(yōu)勢的同時(shí)解決了RNN中容易出現(xiàn)的梯度問題，而GRU神經(jīng)網(wǎng)絡(luò)簡化了循環(huán)單元結(jié)構(gòu)，使得訓(xùn)練速度有所提升。但是GRU神經(jīng)網(wǎng)絡(luò)和LSTM神經(jīng)網(wǎng)絡(luò)都只能考慮預(yù)測點(diǎn)過去時(shí)刻的信息而無法考慮未來時(shí)刻的狀態(tài)，使得預(yù)測精度無法進(jìn)一步提高。

BiGRU在單向GRU神經(jīng)網(wǎng)絡(luò)的基礎(chǔ)上增加了一層隱含層，將預(yù)測過程分為前向預(yù)測與后向預(yù)測兩個(gè)方向，并由兩個(gè)方向的隱含層共同決定輸出結(jié)果[18]。BiGRU神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)如圖3所示。

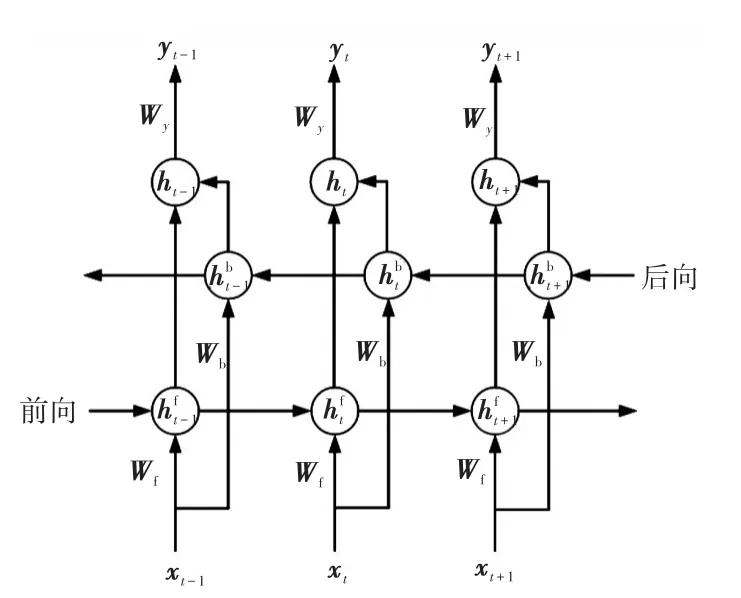
圖3 BiGRU神經(jīng)網(wǎng)絡(luò)Fig.3 BiGRU neural network

圖3中：Wf為前向預(yù)測過程中輸入層到隱含層權(quán)值；Wb為后向預(yù)測過程中輸入層到隱含層權(quán)值；為前向預(yù)測過程的隱含層狀態(tài)；為后向預(yù)測過程的隱含層狀態(tài)。

由圖3可以看出，與單向GRU神經(jīng)網(wǎng)絡(luò)相比較，BiGRU神經(jīng)網(wǎng)絡(luò)將預(yù)測過程分為兩個(gè)方向進(jìn)行，前向過程為傳統(tǒng)的單向GRU神經(jīng)網(wǎng)絡(luò)，后向過程是與前向過程相對(duì)應(yīng)的相反方向的預(yù)測過程，后向預(yù)測過程可以考慮預(yù)測點(diǎn)后面時(shí)刻的數(shù)據(jù)對(duì)當(dāng)前隱含層的影響，而預(yù)測結(jié)果的隱含層狀態(tài)由兩個(gè)方向的隱含層共同決定，故BiGRU神經(jīng)網(wǎng)絡(luò)結(jié)合了預(yù)測點(diǎn)過去和未來的隱含層狀態(tài)，從而在預(yù)測過程中可以進(jìn)一步提高準(zhǔn)確性。

BiGRU神經(jīng)網(wǎng)絡(luò)將兩個(gè)方向的隱含層進(jìn)行疊加進(jìn)而達(dá)到同時(shí)考慮預(yù)測點(diǎn)過去和未來信息的目的，傳統(tǒng)的疊加方式有拼接、求和及取平均值等，這些疊加方式在輸入數(shù)據(jù)較多時(shí)會(huì)出現(xiàn)預(yù)測穩(wěn)定性下降的問題，本文采用了一種對(duì)兩個(gè)方向的隱含層進(jìn)行加權(quán)求和的疊加方式，計(jì)算公式為

式中，o為比例系數(shù)。

雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)通過改變o的值可以改變兩個(gè)方向的隱含層狀態(tài)所占權(quán)重，從而更好地利用兩個(gè)方向的輸出數(shù)據(jù)。與傳統(tǒng)疊加方式相比，加權(quán)求和的方法可以對(duì)兩個(gè)方向信息的疊加比例進(jìn)行更有效地控制，提高了預(yù)測過程的效率。

2 基于Bagging算法的雙向加權(quán)GRU集成神經(jīng)網(wǎng)絡(luò)短期負(fù)荷預(yù)測模型

2.1 Bagging集成算法

集成學(xué)習(xí)將多個(gè)基學(xué)習(xí)器進(jìn)行組合來得到一個(gè)學(xué)習(xí)效果更強(qiáng)的強(qiáng)學(xué)習(xí)器，采用一定的組合策略將基學(xué)習(xí)器進(jìn)行結(jié)合，可以有效利用各個(gè)基學(xué)習(xí)器的特征，從而提高模型的學(xué)習(xí)性能。本文采用集成學(xué)習(xí)中的Bagging集成算法，其基本思想為從初始數(shù)據(jù)集中隨機(jī)有放回地采樣N次，得到N個(gè)訓(xùn)練數(shù)據(jù)集，利用采樣得到的訓(xùn)練數(shù)據(jù)集通過N個(gè)基學(xué)習(xí)器進(jìn)行訓(xùn)練學(xué)習(xí)從而得到N個(gè)預(yù)測模型，對(duì)于回歸問題將N個(gè)預(yù)測模型進(jìn)行等權(quán)重取平均值處理即可得到強(qiáng)學(xué)習(xí)器，基本流程如圖4所示。

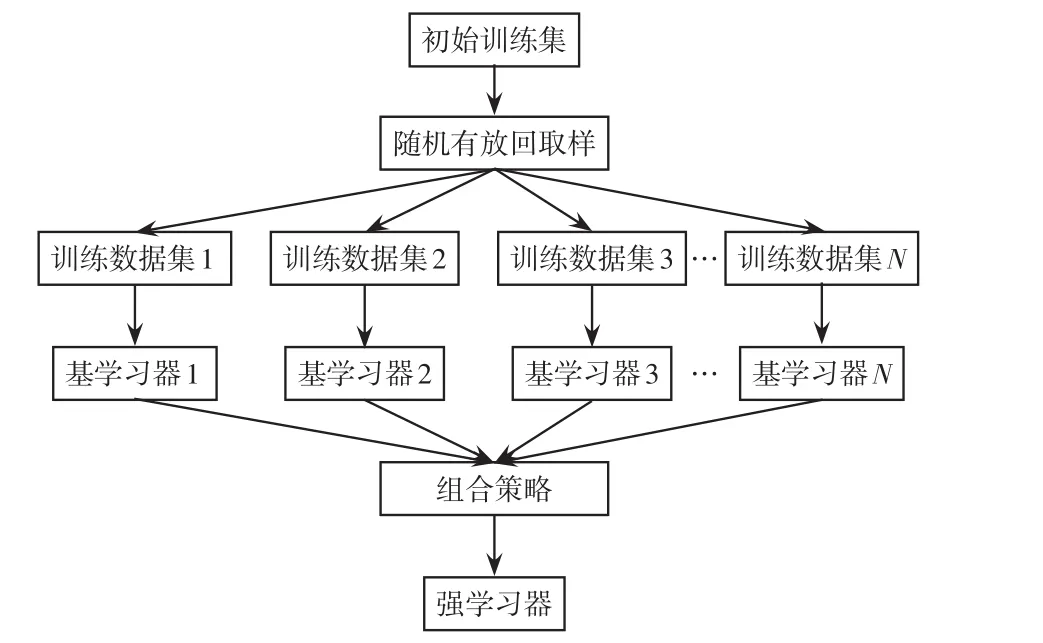
圖4 Bagging算法流程Fig.4 Flow chart of Bagging algorithm

2.2 預(yù)測模型

雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)預(yù)測過程中對(duì)預(yù)測點(diǎn)過去和未來的信息進(jìn)行了充分的利用，可以較好地建立時(shí)間序列相關(guān)模型，但是單一的雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)仍然存在著預(yù)測過程不夠穩(wěn)定、隨機(jī)性較大的問題。Bagging集成算法在建模過程中引入了隨機(jī)取樣[19]，通過結(jié)合多個(gè)基學(xué)習(xí)器的特征可以較好地提高預(yù)測過程中的穩(wěn)定性，優(yōu)化了模型的整體預(yù)測性能，利用Bagging算法對(duì)雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)進(jìn)行集成處理，可以顯著提升預(yù)測模型的泛化能力[20]。將雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)作為Bagging算法中的基學(xué)習(xí)器，利用生成的N個(gè)訓(xùn)練數(shù)據(jù)集對(duì)N個(gè)雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)模型進(jìn)行并行訓(xùn)練，基于Bagging算法的雙向加權(quán)GRU集成神經(jīng)網(wǎng)絡(luò)短期預(yù)測模型結(jié)構(gòu)如圖5所示。

圖5 基于Bagging算法的雙向加權(quán)GRU集成神經(jīng)網(wǎng)絡(luò)模型Fig.5 Modelof bi-directional weighted GRU neural network integrated by Bagging algorithm

模型結(jié)構(gòu)主要分為輸入層、Bagging取樣層、雙向加權(quán)GRU層、Bagging集成層和輸出層。首先從輸入層的初始訓(xùn)練集中隨機(jī)有放回的抽取樣本數(shù)為v的子數(shù)據(jù)集，將此抽樣過程重復(fù)N次從而得到N個(gè)子數(shù)據(jù)集，隨機(jī)有放回的取樣過程使得N個(gè)子數(shù)據(jù)集之間互不影響。將雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)作為Bagging集成算法中的基學(xué)習(xí)器，把N個(gè)子數(shù)據(jù)集作為雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)的輸入，通過N個(gè)雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)模型進(jìn)行預(yù)測，從而得到N個(gè)預(yù)測輸出值，N個(gè)神經(jīng)網(wǎng)絡(luò)模型的預(yù)測過程是并列運(yùn)行的，一定程度上加快了模型的訓(xùn)練速度。在回歸問題中，Bagging集成算法的組合策略為等權(quán)重取平均值法，將得到的N個(gè)預(yù)測輸出值進(jìn)行取平均值處理，即可得到基于Bagging算法的雙向加權(quán)GRU集成神經(jīng)網(wǎng)絡(luò)的輸出值。

在雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過程中，通過粒子群優(yōu)化PSO（particle swarm optimization）算法對(duì)前向和后向傳播過程中的權(quán)重wr、wz、ur、uz、w、u、wy以及比例系數(shù)o進(jìn)行尋優(yōu)[21]。PSO算法是一種源于鳥類覓食行為的最優(yōu)化算法，可以較好地解決傳統(tǒng)梯度下降算法在訓(xùn)練過程中精度有所下降的問題，雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)的預(yù)測過程流程圖如圖6所示。

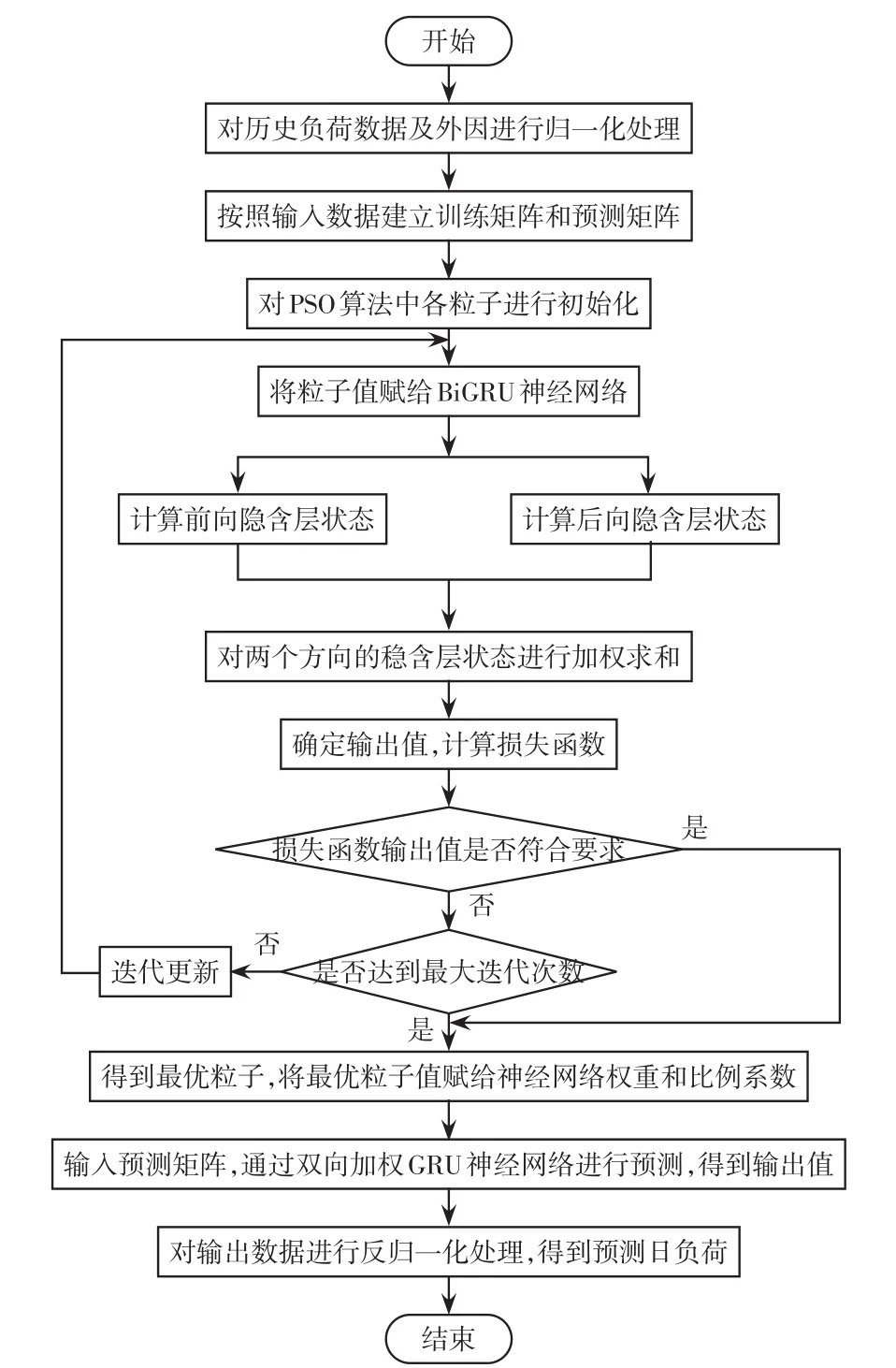
圖6 雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)預(yù)測流程Fig.6 Flow chart of prediction using bi-directional weighted GRU neural network

預(yù)測模型首先對(duì)輸入數(shù)據(jù)進(jìn)行歸一化處理，建立訓(xùn)練矩陣與預(yù)測矩陣，然后將訓(xùn)練矩陣作為輸入，經(jīng)由前向與后向兩個(gè)方向進(jìn)行矩陣計(jì)算，兩個(gè)方向的預(yù)測過程是單獨(dú)進(jìn)行的，得到兩個(gè)方向的隱含層狀態(tài)，并對(duì)兩個(gè)方向的隱含層狀態(tài)進(jìn)行加權(quán)求和，通過計(jì)算得到當(dāng)前的負(fù)荷值。利用PSO算法對(duì)神經(jīng)網(wǎng)絡(luò)權(quán)值和加權(quán)比例系數(shù)進(jìn)行尋優(yōu)，將損失函數(shù)作為目標(biāo)函數(shù)，得到使得損失函數(shù)達(dá)到最優(yōu)時(shí)的權(quán)值與比例系數(shù)。按照最優(yōu)權(quán)值與最優(yōu)比例系數(shù)，結(jié)合預(yù)測矩陣，經(jīng)由所提預(yù)測模型計(jì)算得到負(fù)荷輸出值，并對(duì)負(fù)荷值進(jìn)行反歸一化處理，即可得到負(fù)荷的預(yù)測值，達(dá)到負(fù)荷預(yù)測的目的。

2.3 損失函數(shù)

本文所提模型中，將損失函數(shù)作為預(yù)測模型的目標(biāo)函數(shù)，通過不斷迭代得到最優(yōu)解。選取均方誤差函數(shù)作為損失函數(shù)[22]，即

式中：n為預(yù)測點(diǎn)的個(gè)數(shù)；Yi為第i個(gè)預(yù)測點(diǎn)的實(shí)際負(fù)荷值；yi為第i個(gè)預(yù)測點(diǎn)的預(yù)測值。

3 算例分析

3.1 數(shù)據(jù)處理

為驗(yàn)證所提模型的預(yù)測效果，按照所提模型對(duì)某地區(qū)負(fù)荷進(jìn)行預(yù)測，本文所采用數(shù)據(jù)源于某地區(qū)電網(wǎng)真實(shí)負(fù)荷數(shù)據(jù)。歷史負(fù)荷數(shù)據(jù)是負(fù)荷預(yù)測過程中的最重要數(shù)據(jù)，但電力負(fù)荷受多種因素的影響，在預(yù)測過程中還應(yīng)考慮溫度、日期類型（工作日，休息日）等多個(gè)因素的影響。

神經(jīng)網(wǎng)絡(luò)的輸入數(shù)據(jù)包括歷史負(fù)荷數(shù)據(jù)、溫度數(shù)據(jù)和日類型數(shù)據(jù)。在訓(xùn)練過程中，每15 min取一個(gè)負(fù)荷點(diǎn)，即一天內(nèi)選取96個(gè)負(fù)荷點(diǎn)進(jìn)行訓(xùn)練。將預(yù)測日前10 d的負(fù)荷數(shù)據(jù)作為訓(xùn)練樣本并以此構(gòu)造訓(xùn)練矩陣，將預(yù)測日當(dāng)天的負(fù)荷數(shù)據(jù)作為測試樣本構(gòu)造預(yù)測矩陣。訓(xùn)練矩陣和預(yù)測矩陣的歷史負(fù)荷數(shù)據(jù)選取與樣本中預(yù)測日相關(guān)性最大的前3 d負(fù)荷數(shù)據(jù)，具體包括預(yù)測日（第k天）預(yù)測時(shí)刻t前3 d的第t-1、t、t+1時(shí)刻的負(fù)荷值共9維數(shù)據(jù)。溫度數(shù)據(jù)具體包括預(yù)測日（第k天）前3 d以及預(yù)測日當(dāng)天的日最高溫度、日最低溫度和日平均溫度共12維數(shù)據(jù)。日類型數(shù)據(jù)中具體包括預(yù)測日（第k天）前3 d以及預(yù)測日當(dāng)天的日類型共4維數(shù)據(jù)，將工作日日類型定為1，休息日日類型定為0，故雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)采取25維輸入矩陣。輸出矩陣為1維矩陣，即為預(yù)測日預(yù)測時(shí)刻t的負(fù)荷預(yù)測值。

電力系統(tǒng)短期負(fù)荷預(yù)測有多種評(píng)價(jià)標(biāo)準(zhǔn)，本文采用平均絕對(duì)百分比誤差Emape和最大相對(duì)誤差Emax來對(duì)預(yù)測效果進(jìn)行評(píng)價(jià)，平均絕對(duì)百分比誤差的計(jì)算公式為

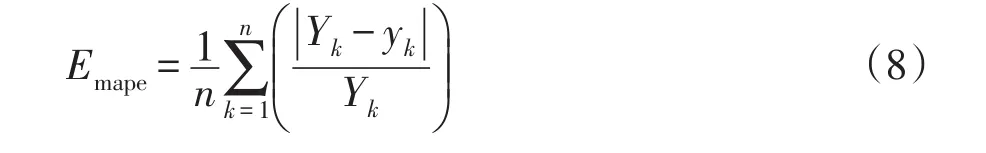
式中：Yk為預(yù)測點(diǎn)的真實(shí)負(fù)荷值；yk為預(yù)測負(fù)荷值；n為預(yù)測點(diǎn)個(gè)數(shù)。

3.2 仿真結(jié)果分析

為了比較預(yù)測結(jié)果，將BP神經(jīng)網(wǎng)絡(luò)預(yù)測模型（模型1）、LSTM神經(jīng)網(wǎng)絡(luò)預(yù)測模型（模型2）、GRU神經(jīng)網(wǎng)絡(luò)預(yù)測模型（模型3）、BiGRU神經(jīng)網(wǎng)絡(luò)預(yù)測模型（模型4）與本文提出的基于Bagging算法的雙向加權(quán)GRU集成神經(jīng)網(wǎng)絡(luò)短期負(fù)荷預(yù)測模型（模型5）進(jìn)行對(duì)比驗(yàn)證。5種模型均采用25-10-1的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，其中模型1訓(xùn)練次數(shù)取10 000次，訓(xùn)練的精度要求取0.01；模型2、模型3和模型4訓(xùn)練次數(shù)都取8 000次，梯度步長取0.001；模型5中PSO算法的粒子數(shù)取50個(gè)，訓(xùn)練次數(shù)取900次，學(xué)習(xí)因子取1.795，粒子速度的最大值取0.4，最小值取-0.4，基學(xué)習(xí)器的數(shù)目取6個(gè)，5種模型的預(yù)測效果如圖7和圖8所示。

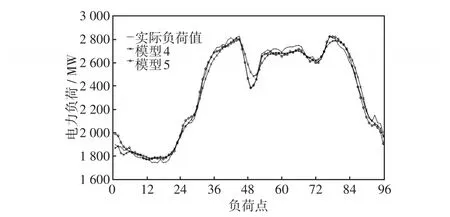
圖8 模型4和5預(yù)測的負(fù)荷曲線Fig.8 Load curves predicted by models 4 and 5

5種預(yù)測模型的Emape和Emax如表1所示。

由圖7可以得出，模型5所得曲線與實(shí)際負(fù)荷的擬合度更高。由表1可以得出，與模型1、模型2、模型3、模型4相比，模型5的 Emape分別降低了2.12%、0.71%、0.66%、0.21%，Emax分別降低了4.37%、0.31%、0.88%、0.45%，說明本文所提模型具有較高的預(yù)測精度，預(yù)測效果較好。為了驗(yàn)證所提模型的穩(wěn)定性，分別通過模型4和模型5對(duì)某地區(qū)連續(xù)一周內(nèi)的負(fù)荷進(jìn)行預(yù)測，預(yù)測誤差如表2所示。

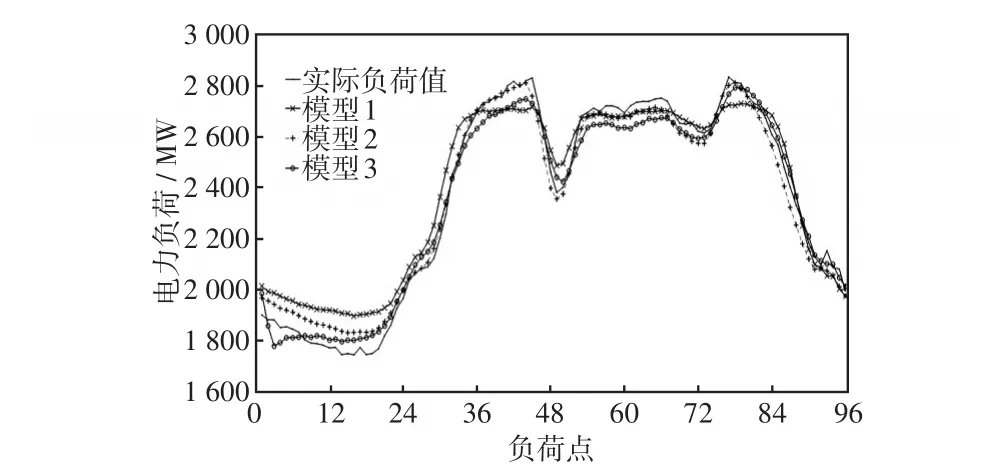
圖7 模型1～3預(yù)測的負(fù)荷曲線Fig.7 Load curves predicted by models 1，2，3

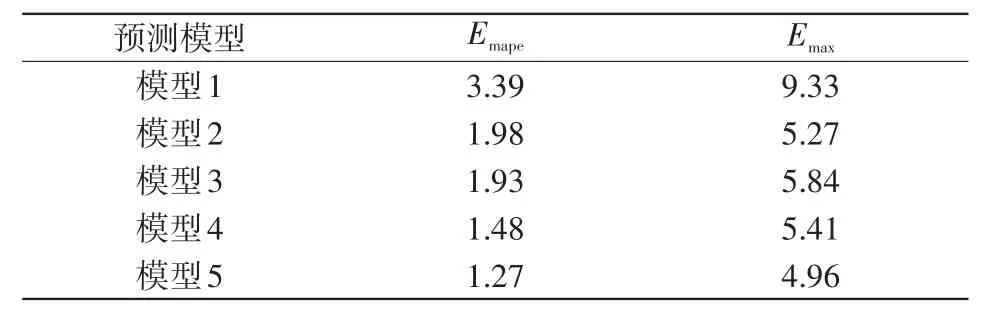
表1 5種模型的預(yù)測誤差對(duì)比Tab.1 Comparison of prediction error among five models %

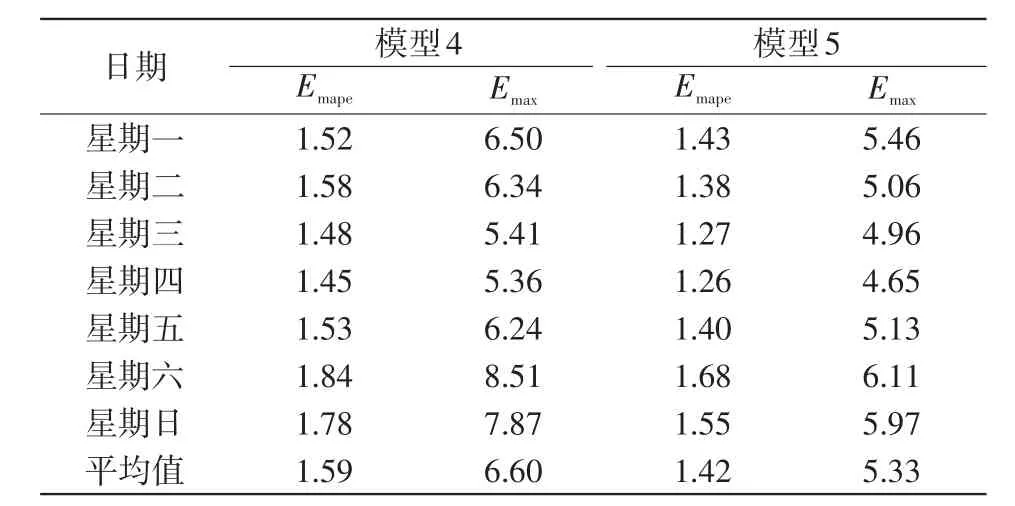
表2 兩種預(yù)測模型一星期內(nèi)預(yù)測誤差對(duì)比Tab.2 Comparison of weekly prediction errors between two prediction models %

由表2可以看出，與模型4相比，模型5在一星期內(nèi)Emape的平均值降低了0.17%，Emax的平均值降低了1.27%，模型5在一星期內(nèi)的整體預(yù)測性能要優(yōu)于模型4，在休息日期間兩種模型的預(yù)測精度有所下降，主要原因是休息日的訓(xùn)練數(shù)據(jù)相對(duì)較少。從一星期內(nèi)的預(yù)測誤差可以得出，本文所提模型5有較高的預(yù)測精度，預(yù)測過程較為穩(wěn)定，符合實(shí)際應(yīng)用的要求。

4 結(jié)語

本文提出了一種基于Bagging算法的雙向加權(quán)GRU集成神經(jīng)網(wǎng)絡(luò)短期負(fù)荷預(yù)測模型，BiGRU神經(jīng)網(wǎng)絡(luò)解決了RNN中容易出現(xiàn)的梯度問題，并且可以同時(shí)考慮負(fù)荷點(diǎn)過去和未來時(shí)刻的信息，對(duì)BiG?RU神經(jīng)網(wǎng)絡(luò)中兩個(gè)方向的隱含層狀態(tài)進(jìn)行加權(quán)求和處理，可以對(duì)兩個(gè)方向的信息進(jìn)行更充分地利用。通過Bagging算法對(duì)雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)進(jìn)行集成，有效提高了模型的泛化能力。在預(yù)測過程中考慮溫度、日類型等外界因素的影響，并按照某地區(qū)電網(wǎng)真實(shí)負(fù)荷數(shù)據(jù)進(jìn)行驗(yàn)證，與BP神經(jīng)網(wǎng)絡(luò)、LSTM神經(jīng)網(wǎng)絡(luò)、單向GRU神經(jīng)網(wǎng)絡(luò)及BiGRU神經(jīng)網(wǎng)絡(luò)進(jìn)行對(duì)比可以得出，本文所提模型具有較高的預(yù)測精度與預(yù)測穩(wěn)定性。PSO算法和Bagging算法與雙向加權(quán)GRU神經(jīng)網(wǎng)絡(luò)的結(jié)合使得所提模型的訓(xùn)練速度有所下降，在今后的研究中將進(jìn)一步優(yōu)化模型結(jié)構(gòu)。