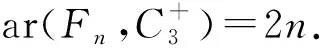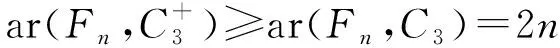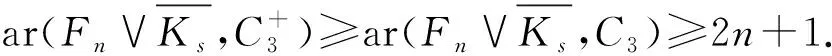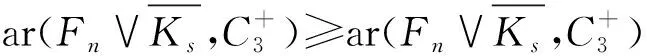一些聯圖的anti-Ramsey數

丁吉麗,邊 紅*，于海征

(1.新疆師范大學數學科學學院，新疆 烏魯木齊 830017;2.新疆大學數學與系統科學學院，新疆 烏魯木齊 830046)

1 預備知識

圖的anti-Ramsey數是由Erd?s等[1]在1973年提出的.若將圖G的邊染色中所有的邊都染成不同的顏色，則稱圖G是彩虹的.圖G的anti-Ramsey數ar(G，H)是指圖G的邊染色中所用的最大顏色數，使得圖G不包含彩虹子圖H[1].Erd?s等[1]最初研究anti-Ramsey數的母圖是完全圖，且對完全圖中的圈和路的anti-Ramsey數提出猜想，并闡明了圖的anti-Ramsey數和圖的Turn數之間有著密切的聯系.圖H的Turn數ex(n，H)是指n個頂點的圖中所包含的最大邊數，使得該圖不包含同構于H的子圖[2].

沿著這條研究主線，學者們研究了完全圖中的其他圖類的anti-Ramsey數，比如：樹[3]、小的二部圖[4]、點不交的圈[5]、匹配[6-8]等.后來，研究anti- Ramsey問題的母圖從完全圖變換成其他的圖類，比如完全二部圖[9-11]、完全分裂圖[12]、超立方體[13]、平面三角剖分圖[14]、超圖[15]等.

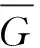
在圖G中，對于?v∈V(G)，?e∈E(G).用C(G)表示圖G所有邊的顏色的集合；C(v)表示與頂點v相關聯的邊的顏色的集合，c(e)表示邊e的顏色.G1和G2是圖G中兩個不同的子圖，E(G1，G2)表示一個端點在G1中，另一個端點在G2中的所有邊的集合,C(G1,G2)表示E(G1，G2)中所有邊的顏色的集合.

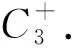
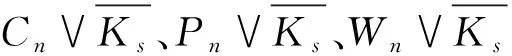
2 主要結果

2.1 聯圖的anti-Ramsey數

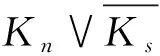
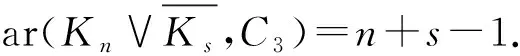
因為C3=K3,所以由定理1易得定理2.

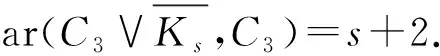
定理3[14]若n≥4,則ar(Wn,C3)=n+1.

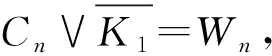
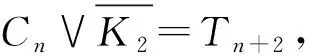
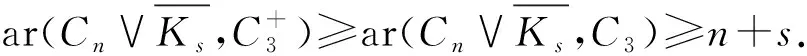
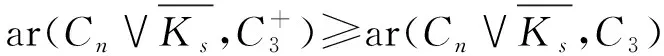
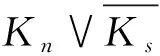
定理6[9]若n≤s,k≤2,則

ar(Kn,s,C2k)=

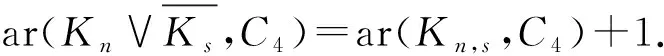
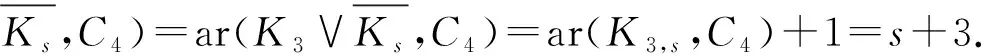
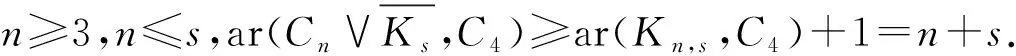
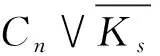
對于n=4的情形，用ar(Kn,s，C4)種顏色對Kn,s的邊染色，使得Kn,s不包含彩虹的子圖C4,用一種新顏色對Cn的邊染色，使得Cn是一個單色圖.

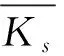
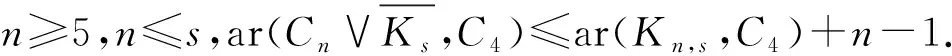
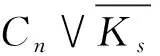
下面根據n的奇偶進行分類討論：

情形1n是奇數.

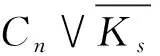
情形2n是偶數.

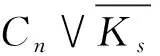
若c(x2zi)=2,則c(xmzi)=2,其中m=2,4,6,…，n;

若c(x2zi)=1,則c(xmzi)=1,其中m=1,2,3,…,n-1,n.

2.2 聯圖的anti-Ramsey數

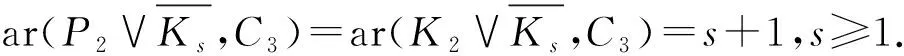
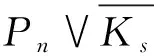
引理1[14]若Ck是邊著色圖G中的一個彩虹圈且k≥4,如果G[Ck]有一條弦，則在G中有一個長度小于k的彩虹圈.

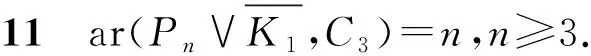
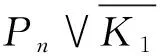
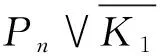
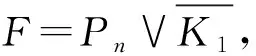
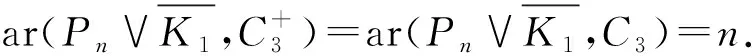
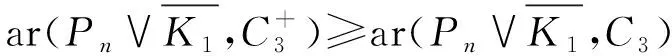
彩虹的C3的位置有兩種，如圖1所示.

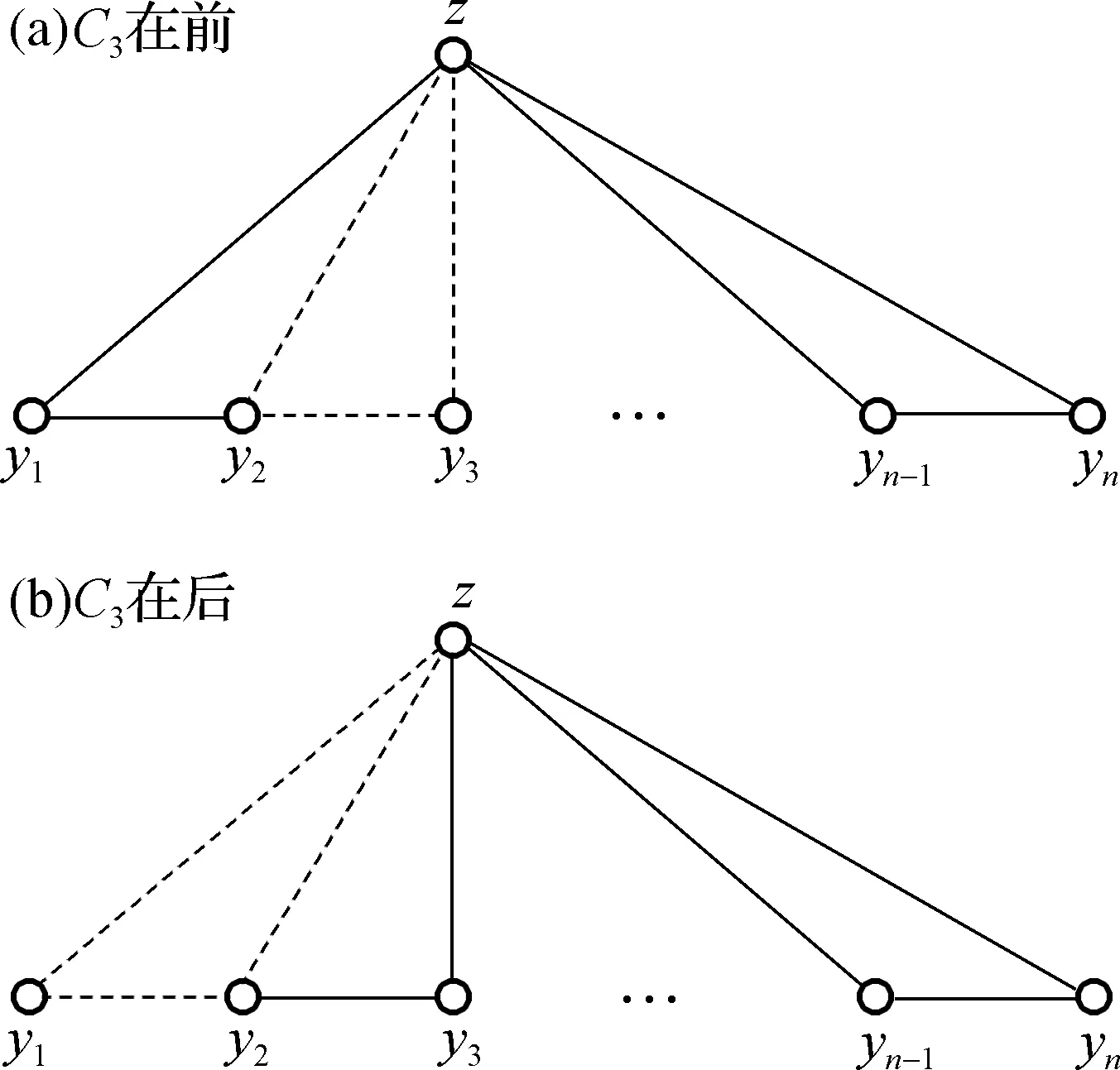
圖中C3的兩種位置Fig.1 Two location of C3 in

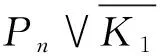
情形1彩虹C3位于前一種位置(圖1(a)).

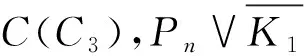
情形2彩虹C3位于后一種位置(圖1(b)).

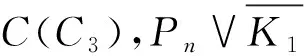
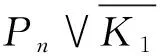
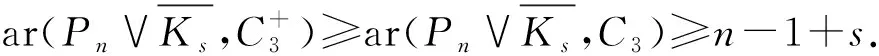
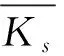
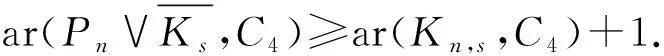
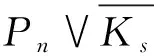
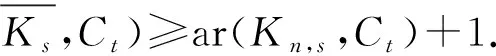
2.3 聯圖的anti-Ramsey數

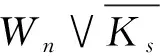
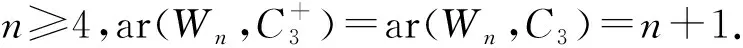
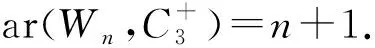
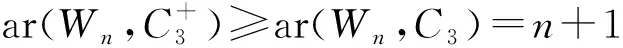
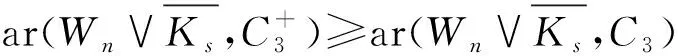
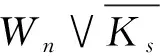
圖中C4的3種位置Fig.2 Three location of C4 in

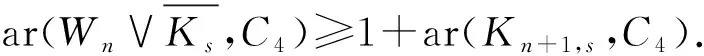
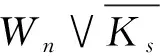
2.4 聯圖的anti-Ramsey數

定理20若n≥2,則ar(Fn，C3)=2n.

證明對于友誼圖Fn，實質上是n個三角形有一個公共頂點的圖.按照這樣的特性，用n種顏色將每個三角形中和公共頂點關聯的兩條邊染成一樣的顏 色，剩余的n條邊用新的n種不同的顏色染色，此時在Fn中一定不含彩虹的C3.因此,ar(Fn，C3)≥2n.

如果用2n+1種顏色對Fn的邊任意染色，根據鴿巢原理，那么至少有一個三角形的3條邊顏色不一樣，即找到一個彩虹的C3.因此，ar(Fn，C3)<2n+1.