求解具有非線性源項的雙側空間分數階擴散方程的樣條方法
陳雪娟,陳景華,2*,章紅梅
(1.集美大學理學院,福建 廈門 361021 ;2.集美大學數字福建大數據建模與智能計算研究所,福建 廈門 361021;3.福州大學數學與計算機科學學院,福建 福州 350108)
近年來,研究者們在湍流、核磁共振、多孔介質中的滲透等系統中都觀察到偏離布朗運動特性的擴散行為,而分數階微分方程能夠較精確地描述具有記憶和遺傳、路徑依賴性質的物理過程[1],因此分數階微分方程目前已被用來描述諸多領域[2-4]中的反常擴散問題.從現實問題中抽象出分數階微分方程之后,如何對分數階微分方程進行求解成為一個迫切的研究課題.目前已有很多文獻討論了分數階微分方程的解析解,但是這些解大多含有特殊函數(比如多變量的Mittag-Leffler函數[5-9]),要計算這些特殊函數相當困難,而且并非所有的分數階微分方程都能得到其解析解,因此研究分數階方程的數值模擬有著重要的理論與應用價值.國內外對分數階微分方程數值解的研究也有一定的進展,主要采用的數值方法是有限差分[10-14]、有限元、譜方法[15-17]等;但是采用二次多項式樣條函數進行數值逼近的研究文獻卻較缺乏.Sousa[18]研究線性分數階擴散方程,借助樣條函數近似離散分數階導數,并在時間上采用Crank-Nicolson離散.Rashidinia等[19]提出一種新的非多項式樣條方法數值求解二階雙曲線方程.Siraj等[20]構造了三次非多項式樣條函數來求解非線性薛定諤方程.陳雪娟等[21]采用基于二次樣條函數的數值方法求解分數階擴散方程,但是處理的是單側分數階導數.較少文獻涉及用樣條方法數值求解雙側分數階導數.由于雙側分數階導數涉及到區間兩個邊界的函數值,比單側分數階導數能更好地模擬反常擴散現象,所以多用于定義空間變量的分數階導數.
本文提出一種基于多項式樣條函數的數值方法,用來求解具有非線性源的雙側空間分數階擴散方程,同時證明了該數值方法是無條件穩定和收斂的.
考慮具有非線性源項的雙側空間分數階擴散方程:
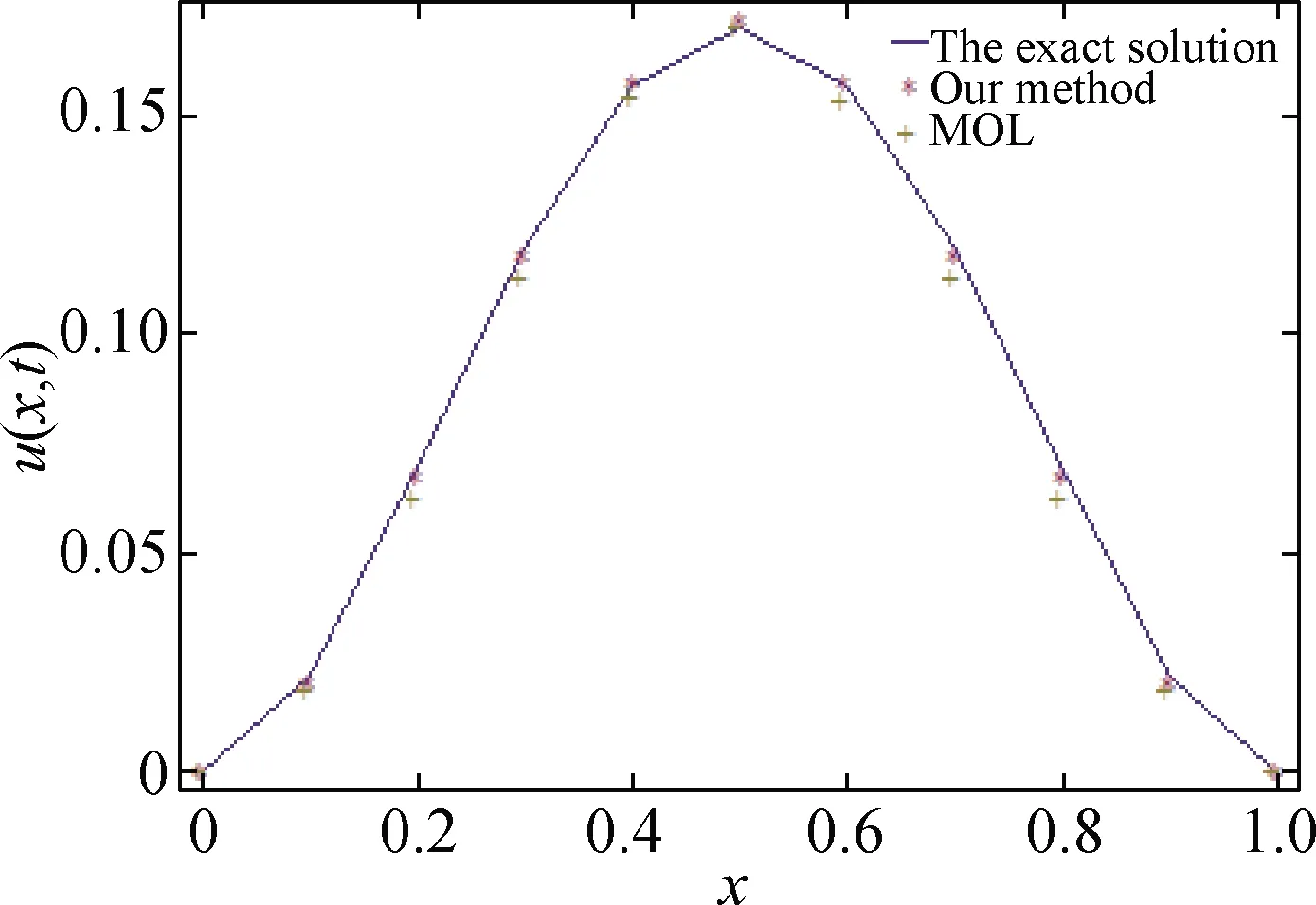
1<α≤2,a (1) 初始條件: u(x,0)=g(x),a (2) 具有Dirichlet零邊界條件: u(a,t)=u(b,t)=0, 0≤t≤T. (3) 這里擴散系數λ1(x,t)>0和λ2(x,t)>0.非線性源項f(u,x,t)滿足局部Lipschitz連續條件[22-23], 即存在某個常數L>0,使得 ‖f(u,x,t)-f(v,x,t)‖≤L‖u-v‖. (4) α階的左、右側Caputo導數分別定義如下[24]: (5) (6) 考慮如下二次多項式樣條函數Pi(x,tj)(xi≤x Pi(x,tj)=ai(tj)(x-xi)2+bi(tj)(x-xi)+ ci(tj),i=0,1,2,…,m-1. (7) 為了確定函數Pi(x,tj)的系數表達式,定義: (8) (9) (10) 由方程(7)~(9)可以計算出: (11) 再由方程(7)和(10),及Caputo分數階導數的定義可以推出: (12) 從而可以確定方程(7)的系數為: (13) 為了使二次函數pi(x,t)在x=xi,i=0,1,2,…,m-1處滿足連續性條件 利用方程(13), 得到如下等式: (14) 進一步,可以計算出等式(14)的局部截斷誤差. O(h2). (15) (16) 這里, (17) 以下建立分數階擴散方程(1)~(3)的差分格式. 由方程(1)可得: (18) 對時間導數采用向后差分格式,得到: o(τ), (19) 及 (20) 從方程(14)和(18)可得以下方程: (21) (22) (23) (24) 因此得到分數階擴散方程(1)~(3)的數值逼近格式(22)~(24),且此數值格式的收斂階為O(hα+τ). 本節討論數值方法的收斂性和穩定性.將方程組(22)寫成更簡單的形式: (25) 為了證明數值方法的穩定性和收斂性,引入引理2. 引理2離散的Gronwall不等式[25].假設fk≥0,ζk≥0,k=0,1,2,…,并且ζk+1≤μζk+τfk,μ=1+C0τ,k=0,1,2,…,ζ0=0,這里C0≥0是常數, 則 由迭代格式(25), 得到誤差方程: (26) 對j=1,2,…,n, 分別定義網格函數[26] 則εj(x)和ρj(x) 可分別展開成Fourier級數: 其中系數為 及 有 這里j=0,1,…,n. (27) 定理1數值離散格式(22)~(24)是無條件穩定的. 證明將式(27)代入迭代格式(26), 得到 則有 經過簡單計算得到下列不等式: 因此有 |ξj|≤(|ξj-1|+τ|ηj-1|). (28) 則|ηj|≤L|ξj|.因此 |ξj|≤(1+τL)|ξj-1|,j=1,2,…,n. (29) 運用上式歸納得到 ‖εn‖2≤(1+Lτ)n‖ε0‖2≤eLT‖ε0‖2. 因此,證明了數值離散格式(25)是無條件穩定的. 根據迭代格式(25)的相容性,得到以下誤差方程: (30) j=0,1,…,n. (31) 定理2數值離散格式(22)~(24)是無條件收斂的,并且存在正常數C>0使得: j=1,2,…,n. 證明將式(31)代入到迭代格式(30)中,得到: 經過簡單的計算得到 2,…,n. (32) 這里C1是正常數. 從而 ‖ej‖2≤(1+τL)‖ej-1‖2+C1(hα+τ). 運用離散的Gronwall不等式(引理2)得到: C1TeLT(hα+τ)=C(hα+τ), (33) 這里C=C1TeLT. 因此,證明了數值離散格式(22)~(24)是無條件收斂的,且收斂為o(hα+τ). 一般分數階微分方程的精確解是很難求得,因此為了說明數值方法的有效性,通常將所得的數值解結果與分數階行方法(method of line,MOL)的解進行比較.分數階MOL其本質是只離散空間變量,將分數階偏微分方程轉換成一組常微分方程加以求解.繼而可以采用解決微分代數系統的工具DASSL來求解.2004年Liu等[27]首次運用分數階MOL求解空間分數階Fokker-Planck偏微分方程. 2u(xi-k+1,tj)+u(xi-k,tj)]}+ 2u(xk,tj)+u(xk-1,tj)]}+ u(xk-1,tj)]}+o(h2). 由此得到左、右側Caputo分數階導數的逼近格式: 2u(xi-k+1,tj)+u(xi-k,tj)]}, 2u(xk,tj)+u(xk-1,tj)]}. 因此,具有非線性源項的雙側空間分數擴散方程(1)~(3)的MOL可以寫成以下形式: (34) 本節給出兩個數值例子來證明所提出的理論分析的有效性. 例1考慮具有非線性源項的分數階擴散方程: (35) 這里系數 λ1(x,t)=0.5Γ(5-α)x2+α(1-x)4et, λ2(x,t)=0.5Γ(5-α)x4(1-x)2+αet, 非線性源項為f(x,t,u)=u(x,t)+u2(x,t)·[-24x2+24x-12+2α(4-α)]. 圖1是方程的精確解、數值格式(22)~(24)的數值解及MOL的數值解在t=1.0時刻的比較.取空間步長h=0.05,時間步長τ=0.01,α=1.5. 圖1 t=1.0時刻,取α=1.5,h=0.05,τ=0.01,數值解與 分數階MOL的解及精確解的比較Fig.1 Comparison of numerical solutions using our method, the MOL, and the exact solution at time t=1.0,α=1.5,h=0.05,τ=0.01 表1顯示了在t=1.0時刻,α=1.5,不同的時間步長和空間步長(空間步長和時間步長的關系為h≈τ-α)下精確解與數值解的最大誤差和誤差率.可以看出 表1 在t=1.0時,取α=1.5,數值解與 精確解的最大誤差及誤差率Tab.1 The maximum errors and error rates for the numerical method relative to the exact solution at time t=1.0,α=1.5 說明數值解的收斂階為o(hα+τ),這與本文中理論分析結果是相一致的. 從圖1和表1中可以看出,基于二次多項式樣條函數的數值方法與精確解很好地吻合. 例2考慮以下具有非線性源項的分數階擴散方程: (36) 這里f(x,t,u)=u(1-u)+x2,此題精確解難以求得.因此考慮將數值解與分數階MOL的數值解進行比較. 圖2顯示在t=1.0時刻, 取α=1.5,h=0.05,τ=0.01時數值解與分數階MOL數值解的比較.圖3顯示了當α=1.5,h=0.05,τ=0.01時, 在不同時刻t=0.3,0.5,1.0的數值解的圖形.圖4顯示了在t=1.0時刻取不同的分數階導數值α=1.5,1.8,2.0時數值解的圖形. 圖2 t=1.0時刻,取α=1.5,h=0.05,τ=0.01,數值解與 分數階MOL數值解的比較Fig.2 Comparison of numerical solutions using our method and the fractional MOL at time t=1.0,α=1.5,h=0.05,τ=0.01 圖3 取α=1.5,h=0.05,τ=0.01,本文方法 在不同時刻的數值解比較Fig.3 Comparison of numerical solutions using our method at different times when α=1.5,h=0.05,τ=0.01 本文提出了一種基于多項式樣條函數的數值離散格式,用于求解具有非線性源項的雙側空間分數階擴散方程,其中的分數階導數采用Caputo分數階導數;同時,提出一種計算分數階微分方程數值解的計算技巧,即分數階MOL.證明了提出的數值離散格式是無條件穩定和收斂的,且收斂階為o(hα+τ)(1<α≤2).最后,給出數值例子證明了方法的有效性.這種樣條方法和分析技術可用于求解和分析其他類型的分數階偏微分方程.1 樣條配置法

1.1 二次多項式樣條函數

1.2 構造數值方法
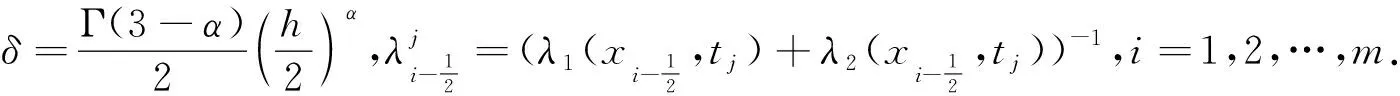
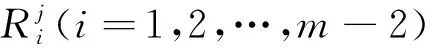
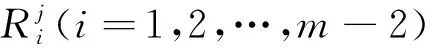
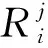
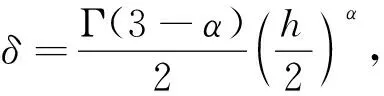
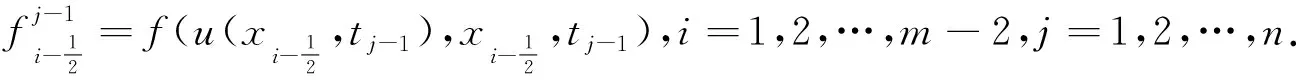

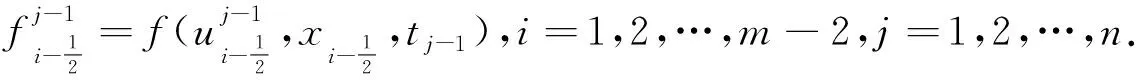
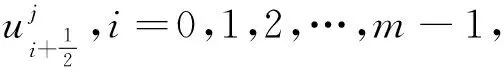
2 數值方法的穩定性和收斂性分析
2.1 穩定性分析
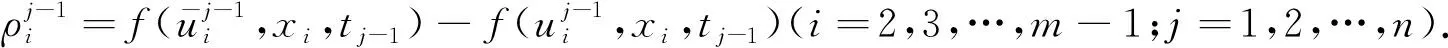
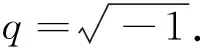
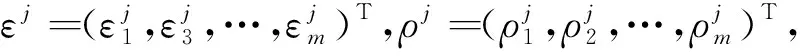



2.2 收斂性分析

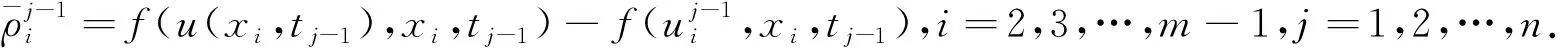
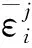

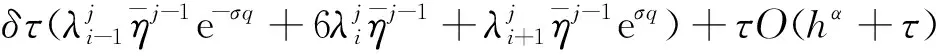
3 分數階行方法
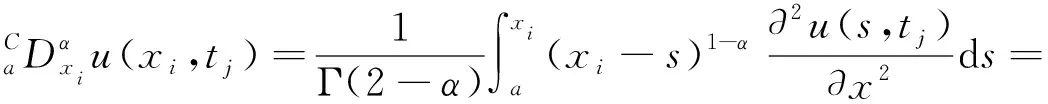

4 數值例子



5 結 論

