4～6歲幼兒有參照估數能力的發展特點

王晶 張俊

[摘 要] 估數能力是個體數概念發展的重要組成部分。本研究以南京市某幼兒園中班和大班共111名幼兒為研究對象，調查4～6歲幼兒有參照估數能力發展的特點。結果表明，大班幼兒有參照估數能力顯著高于中班幼兒;幼兒有參照估數的精準性受到待估數量的影響，待估數量越大精準性越低;情景抽象程度對幼兒有參照估數精準性的影響不顯著;幼兒使用的估數策略是影響其有參照估數精準性的重要因素，幼兒運用“參考量比較”策略時估數精準性較高，幼兒不明確或無法說出估數策略時精準性較低;待估數量與參考量越接近，使用“參考量比較”策略的幼兒越多。成人應注意引導幼兒認識到估數是一種解決日常生活問題的有效方法，從小數量入手開展適合幼兒的估數活動，并引導幼兒分享估數策略。

[關鍵詞] 4～6歲幼兒;數量估計;有參照估數;估數策略

一、問題提出

數學作為一種技能在日常生活中被廣泛運用，但數學在生活中的運用并不總是力爭要得到一個精確的答案。現實生活中人們每天要面對大量的數和量方面的信息，很多時候特別是在一些特定情景中，需要運用數學相關知識和技能對數和量的信息進行模糊的、近似的處理，即估計。估計是日常生活中被廣泛應用的一種技能，例如估計現場大概有多少人看比賽，估計完成家務大約需要多長時間。已有研究發現估計與其他數學能力具有密切的相關性，是一種靈活應用數學知識的適應性問題解決方式，這種問題解決方式正是當代數學教育的一個基本目標。[1]

估計按照操作任務的差異通常被劃分為三個類別：數量估計（numerosity estimation）、測量估計（measurement estimation）和計算估計（computational estimation）。[2][3][4]其中測量估計簡稱估測，布萊特（Bright）將其定義為一種在不使用一般測量工具的情況下，根據某種方法推測出測量結果的心理加工過程。[5]計算估計簡稱估算，道克（Dowker）把計算估計定義為在不進行精確計算的情況下，對算術問題的近似答案做出一個合理的猜測。[6]數量估計簡稱估數，本研究結合已有研究對估數概念的界定，[7][8][9]將估數定義為在沒有足夠時間數出物體的數量，或要數的物體數量過大以及非靜止的物體根本無法做出計數等情況下，通過一定的策略對實物集合給出一個近似的基數值。索德（Sowder）認為估算、估測和估數各需要不同的理解和技能，雖然估測和估數需要某些相關的技能，但估測是對連續量的估計，而估數是對離散量的估計，因此兩者也是不同的。[10]

目前，美國、日本、英國和荷蘭等國家已陸續將估計的相關內容納入數學教育中，我國最早是在1999年教育部頒布的《九年義務教育全日制小學數學教學大綱（試用修訂版）》中正式強調了估計教學的重要性。但各國的數學課程目標設置中基本只強調了小學及以上年齡段的估計教學，并且由于該年齡階段更注重兒童的計算能力，因此多為與估算相關的內容，與估測和估數相關的內容涉及較少。[11][12][13]由于估測和估算能力的發展需要建立在精準測量和計算的基礎上，難度較大且不適用于幼兒階段的數學教育。估數相對更容易被幼兒所掌握，尤其借助參考量進行估數能夠豐富幼兒的估數策略，有效且快速地提高幼兒的估數能力。有參照估數能力的發展是幼兒估數從生疏向熟練轉換的重要過程，因此本研究聚焦探究幼兒有參照估數能力的發展特點。

估數作為一種數量加工方式與精準計數不同，估數體現的是一種通過感性經驗進行數量鑒別和判斷的能力。已有研究證明，幼兒已具備初步的估數能力，并提出了要關注幼兒估數能力的發展和培養。[14][15][16][17]但目前國內外關于估數的研究主要集中在中小學階段，包括對估數的數量表征方式、精準性、策略運用和教學等方面的研究。[18][19][20][21][22]關于幼兒估數和幼兒有參照估數的研究很少，也沒有詳細介紹幼兒估數時參考量的運用情況。已有研究中關于情景抽象程度的差異對幼兒有參照估數精準性的影響是否顯著，還未形成統一結論，[23][24]有待研究者進一步探究，以期豐富該領域的研究，進而幫助幼兒園教師在更全面地了解幼兒估數能力發展特點的基礎上，引導幼兒在日常生活中積累估數經驗和解決相關問題。

二、研究方法

（一）研究對象

已有研究發現，有無參考量對小班幼兒的估數沒有影響，中班幼兒才開始表現出對參考量的初步利用和把握。[25]因此本研究選取南京市某幼兒園兩個中班和兩個大班共111名幼兒作為研究對象。中班幼兒年齡4～5周歲，平均月齡為61.81個月（SD=3.36），男生31名，女生27名，共58名。大班幼兒年齡5～6周歲，平均月齡為74.45個月 （SD=3.72），男生32名，女生21名，共53名。

（二）測查工具

已有研究中關于估數情景的抽象程度對幼兒有參照估數的精準性是否有影響，還未形成統一的結論。[26][27]本研究參考已有研究所涉及的估數情景，選擇從具體逐漸過渡到抽象的實物呈現方式、實物圖片呈現方式和數點呈現方式作為探究幼兒有參照估數能力的三種情景，測查任務也因此分為三部分。三種情景下的待估數量均為：數量15、數量20、數量35、數量50，且不同情境和待估數量下提供的參考量均為數量10。

1. 實物呈現情景下幼兒有參照估數能力的測查。

根據趙振國已有相關研究中的估數測查工具改編而成。[28][29]測查材料是將直徑為1.5 cm、邊緣和中心厚度分別為0.2 cm和0.1 cm的黑色4孔紐扣，均勻地粘在厚度約為0.2 cm的A4紙張大小的白色紙板上，紐扣之間的間隔距離大致相等，隨機排列成不同的圓形或橢圓形。

2. 實物圖片呈現情景下幼兒有參照估數能力的測查。

根據本研究中實物呈現情景下有參照估數的測查工具改編而成。測查材料是用數碼相機從正上方拍攝實物呈現情景下的測查材料（粘有不同數量紐扣的硬紙板），拍攝后統一處理為與A4紙張相同大小的圖片，圖片背景為白色，圖片上的紐扣圖案為黑色。

3. 數點呈現情景下幼兒有參照估數能力的測查。

根據本研究中實物呈現情景下有參照估數和實物圖片呈現情景下有參照估數的測查工具改編而成。測查材料是用計算機在A4白色紙上打印黑色圓點，黑色圓點的大小、間隔及排列形式與實物呈現情景下的紐扣一致。

（三）測查程序

主試核對測查工具和材料，并將測查工具正面朝下擺放整齊，以免幼兒提前看到。帶領幼兒到熟悉的教室，和幼兒建立融洽的關系。測查之初主試請幼兒先對參考量10進行估計，并通過點數來確認所提供的參考量確實是10。同時，為了避免情景呈現的先后順序對幼兒有參照估數的結果產生影響，測查過程中按順序輪換呈現實物、實物圖片和數點情景的任務及相關材料，（如A幼兒呈現情景的順序是：實物—實物圖片—數點。B幼兒呈現情景的順序就是：實物圖片—數點—實物。C幼兒呈現情景的順序則是：數點—實物—實物圖片。依此類推）每種情景下的待估數量（15、20、35、50）各測查1次，即每種情景共測查4次。其中參考量10呈現3秒，待估數量15、20呈現4秒，待估數量35、50呈現5秒。

測查指導語如下（以數點情景為例）：“小朋友，請你不要數，來看看這里大概有多少個黑色圓點？”（主試拿出參考量，呈現3秒鐘后收起，等待幼兒給出估計值）“那請你數一下這里有多少個黑色圓點？”（再次呈現參考量直至幼兒點數清楚）“小朋友，你看這里（手指在參考量上畫一圈）是你剛才數過的黑色圓點，一共有10個，現在請你根據這些黑色圓點（手指在參考量上再畫一圈），不要數，來看看這里（手指在待估數量上畫一圈，并在X秒后收起）大概有多少個黑色圓點？”（幼兒給出答案后追問，并記錄幼兒回答的內容）“你是怎么知道的呢？”

測查過程中主試將幼兒的基本信息、估數結果和所觀察到的幼兒動作及語言記錄下來，并根據表1對幼兒的有參照估數進行計分。三種情景下各有4個待估數量（也就是4個題目），只有幼兒進行“合理的估數”時才能計1分，其他情況均計0分。因此，每種情景的滿分為4分，三種情景滿分共12分。

主試在測查過程中要著重觀察幼兒估數時的眼部、頭部和手部動作，以及幼兒的語言，并追問幼兒所運用的策略，對幼兒的行為和語言進行客觀地記錄。雖然主試在測查過程中強調“不要數，來看看這里大概有多少顆紐扣”，并且通過控制待估數量呈現的時間使幼兒無法在短時間內完成點數，但依舊有很多幼兒快速點數了一部分數量后，根據所點數的數量進行估數，即“利用數數”策略。因此，本研究參考克里蒂斯（Crites）對估數策略的分類方法：不知道、眼球效應、基準比較、分解—重組、其他。[30]將“利用數數”這一策略從“其他”中提取出來，單獨作為一類估數的重要策略進行統計，最終確定幼兒有參照估數的策略為6種：不知道、眼球效應、參考量比較、分解—重組、利用數數、其他。“不知道”是指幼兒不能對自己的估數給出相關的解釋，如幼兒回答“我不知道”或選擇沉默;“眼球效應”指的是幼兒通過眼部直覺對待估物體進行估數，如幼兒回答“我是看出來的”“看起來像XX”或伴有明顯的眼部動作等;“參考量比較”是指幼兒將待估物體的數量與所給參考量或自己設定的參考量進行比較，如幼兒回答“這個比10多一點”“這個和剛才的差不多”等;“分解—重組”是指幼兒把待估物體分解成不同的部分，然后通過重新組合進行估數，如幼兒回答 “有4個10”“一共3排，每排10個”等;“利用數數”指幼兒通過點數一部分數量來估計整個集合的數量，如觀察到幼兒頭部和眼睛有明顯的點數動作，或幼兒回答“我沒有數完，一起好像有40個”;除此之外，當主試無法通過分析幼兒的動作和語言判斷出所運用的具體策略時，則歸入“其他”，如幼兒回答“我媽媽告訴我的”“猜/想/感覺出來的”（但沒有具體說明是如何“猜/想/感覺出來的”）等。

整個測查由3名主試輪流進行。每次測查由1名主試單獨負責，時間控制在10～15分鐘。測查結束后，主試給幼兒發放小禮品，以表示對幼兒的鼓勵和感謝，并將幼兒安全送回所在班級或教室。

（四）重測信度和評分者信度

1. 重測信度。

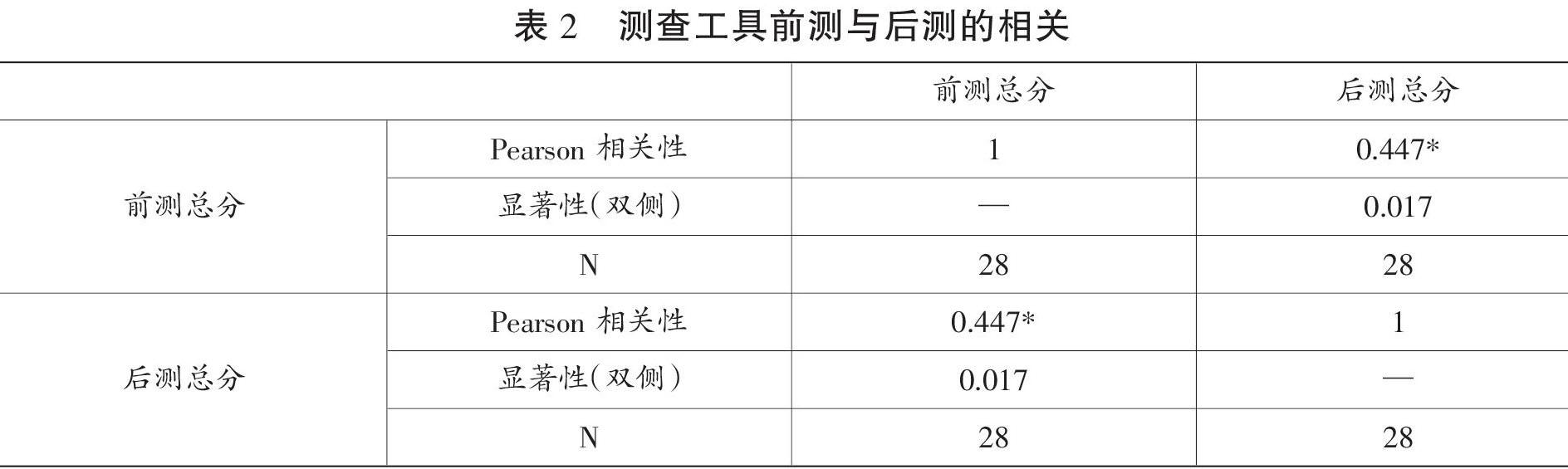
本研究通過對同一群參與者進行兩次測查（間隔一個星期左右），分析兩次測查的誤差程度，考察測查工具是否具有重測信度。表2中的數據顯示前測和后測結果在0.05水平上顯著相關，即本研究具有較高的重測信度。

2. 評分者信度。

本研究的主試及評分者共有三人，為保證研究數據收集的客觀性，本研究通過檢驗評分者A、B、C三者之間的評分是否一致，來衡量主試的評分者信度。

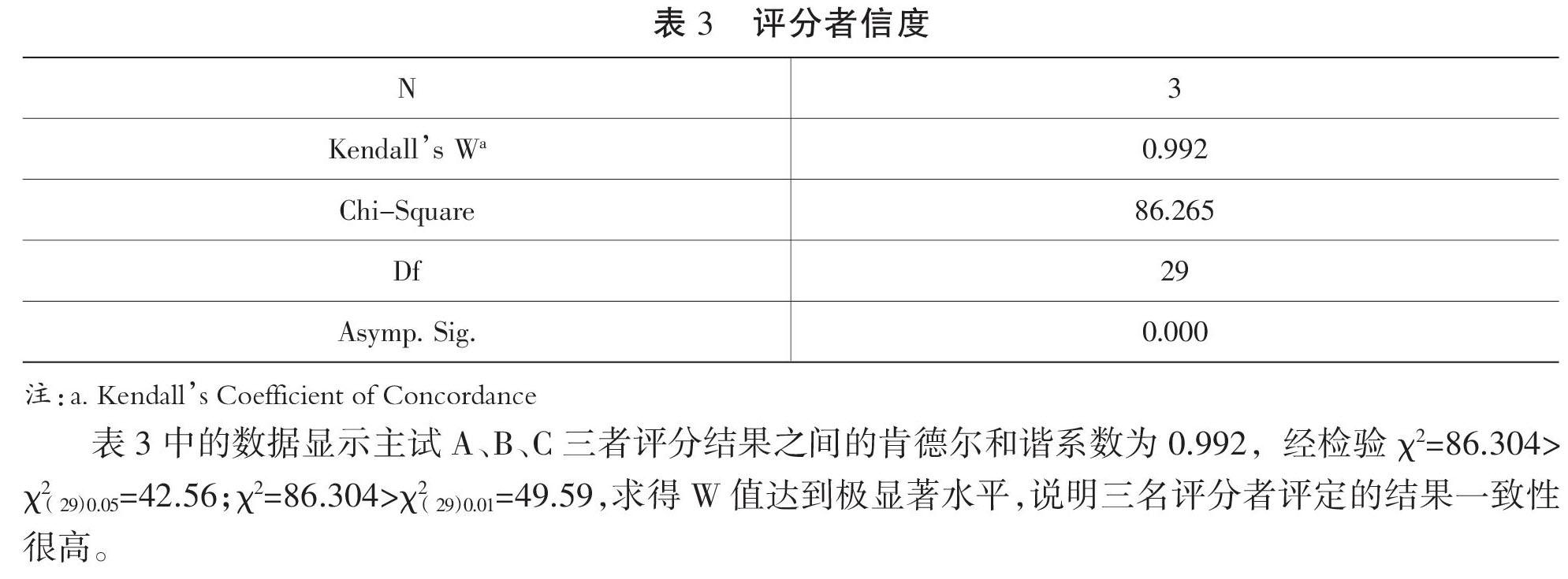
表3中的數據顯示主試A、B、C三者評分結果之間的肯德爾和諧系數為0.992，經檢驗χ2=86.304>χ2（29）0.05=42.56;χ2=86.304>χ2（29）0.01=49.59，求得W值達到極顯著水平，說明三名評分者評定的結果一致性很高。

（五）數據的處理

本研究運用SPSS對數據進行分析和匯總，首先對測查工具進行重測信度分析，再進行評分者信度分析，最后分析幼兒年齡、估數情景和待估數量對幼兒有參照估數發展水平的影響及策略運用的情況。

三、研究結果與分析

（一）三種情景下幼兒對不同數量進行合理估數的占比

本研究發現（見表4和表5），中班和大班幼兒三種情景下對數量15、20、35、50的有參照估數4個水平的百分比各不相同。中班46.6%的幼兒在三種情景下都能夠對數量15進行合理的估數（水平4），伴隨三種情景下待估數量的增大，能夠進行合理估數的幼兒百分比呈現下降趨勢。以實物情景為例，待估數量從15向50遞增，合理估數的幼兒百分比則從46.6%下降至13.8%。估數情景的抽象程度越高，能夠進行合理估數的幼兒總占比越少，數點情景下合理估數的幼兒總占比<實物圖片情景下合理估數的幼兒總占比<實物情景下合理估數的幼兒總占比。

大班超過一半的幼兒在三種情境下能夠對數量15和數量20進行合理的估數。與中班幼兒不同，大班幼兒沒有表現出伴隨待估數量的增大則能夠進行合理估數的幼兒百分比下降的趨勢，也沒有發現估數情景的抽象程度越高則能夠進行合理估數的幼兒總占比越少的趨勢。由此可見，中班和大班幼兒三種情景下的有參照估數能力發展存在差異，中班幼兒的合理估數能力受待估數量大小和情景抽象程度的影響大于大班幼兒。

（二）年齡、情景、數量對幼兒有參照估數發展水平的影響

本研究對幼兒有參照估數能力的發展水平進行了數據收集和處理，并對數據進行2（年齡）×3（情景）×4（數量）的混合因素方差分析。數據顯示（見表6），年齡的主效應顯著，F（1，109）=21.38，P<0.0005，η2=0.16，大班幼兒（M=0.47，SE=0.04）有參照估數的發展水平顯著高于中班幼兒（M=0.24， SD=0.03）。數量的主效應顯著，F（3，327）=45.83，P<0.0005，η2=0.30，隨著數量的增加，幼兒有參照估數的發展水平逐漸降低。對數量15的有參照估數發展水平（M=0.58，SE=0.04）顯著大于對數量20（M=0.41，SE=0.03）、35（M=0.23，SE=0.03）、50（M=0.22，SE=0.03）的有參照估數發展水平，對數量20的有參照估數發展水平顯著大于對數量35、50的有參照估數發展水平。但對數量35和50的有參照估數發展水平差異不顯著，其他主效應和交互作用均不顯著，Fs<2.18。

（三）幼兒有參照估數策略運用的特點

1. 中、大班幼兒的估數策略分析和比較。

本研究通過卡方檢驗，發現中班和大班幼兒在各種策略的運用上差異顯著，χ2=115.41，P<0.0005。如表7所示，分別有26.4%的中班幼兒和19.2%的大班幼兒不能說出有參照估數時所運用的策略。中班幼兒幾種策略運用的百分比相差較大，其中“參考量比較”策略運用的最多，“分解—重組”和“利用數數”策略運用得很少。大班幼兒雖然也是“參考量比較”策略運用的最多，但幾種策略運用的百分比相差較小。

2. 中、大班幼兒合理估數時的策略分析和比較。

本研究通過卡方檢驗發現中班和大班幼兒在合理估數情況下各種策略的運用差異顯著，χ2= 46.99，P<0.0005。如表8所示，幼兒估數合理時運用策略“參考量比較”的占比與其他非參考量比較策略的占比差異明顯，其中運用 “參考量比較”策略的幼兒最多，占比31.9%，而其他非參考量比較的策略占比相對較少，如“不知道”占比6.3%、“眼球效應”占比18.0%、“分解—重組”占比10.9%。除此之外，當幼兒不明確或無法說出估數策略時精準性較低。中班幼兒較多運用“眼球效應”“參考量比較”和“其他”策略，較少運用“不知道”“分解—重組”和“利用數數”策略。大班幼兒則較多運用“參考量比較”策略，其他的策略運用較少。

3. 幼兒有參照估數過程中對參考量的運用情況。

本研究的111名被試中共有50人在有參照估數過程中運用了參考量，占總人數的45.0%，其中中班有22人，大班有28人。本研究發現幼兒運用參考量進行估數主要有三種情況：“利用參考量進行比較”，指幼兒將待估物體的數量與參考量進行對比;“利用參考量進行分解—重組”，指幼兒將待估物體的數量按照參考量進行分解和重組;“回看參考量的眼球效應”，指幼兒在估數過程中伴有明顯的觀看參考量的眼部動作。其中“利用參考量進行比較”的幼兒最多，占比56.60%;“利用參考量進行分解—重組”的幼兒占比18.24%;“回看參考量的眼球效應”的幼兒占比25.16%。所有被試中有12名幼兒在運用參考量進行估數時，并不是只運用了三種策略中的某一種策略，而是同時運用了三種策略中的兩種及以上。

本研究發現幼兒在運用參考量進行估數時，隨著待估數量的增大，參考量的運用逐漸減少，對數量15、20、35、50進行估數時運用參考量的次數，占總體的百分比分別是44.7%、28.3%、14.5%、12.6%。除此之外，本研究還發現，不同幼兒在同樣的有參照估數任務中會選擇運用不同的策略，如實物呈現情景下對數量35的估數，有的幼兒運用“參考量比較”策略，有的幼兒則運用“分解—重組”策略。同一個幼兒在不同的估數任務中所使用的估數策略較一致，但也出現了根據情景呈現順序先后和待估數量的不同而運用不同估數策略的情況，如幼兒A在所有的估數任務中大多運用“眼球效應”策略，但在實物呈現情景下對數量50進行估數時運用了“參考量比較”策略。

四、討論

（一）幼兒有參照估數精準性的年齡特點

已有研究認為估數精準性受個體差異的影響較大，不同年齡階段的幼兒具有不同水平的估數能力，幼兒的估數精準度隨著年齡的增長而提高，[31][32][33][34][35]然而目前針對幼兒的有參照估數精準性的研究并不多。本研究通過對幼兒有參照估數的精準性測查發現，中班幼兒的有參照估數發展水平處于“合理估計”的比例為24.4%，大班則上升到47.1%。這種年齡差異不僅體現在不同的估數情景中，還體現在對不同數量進行估數的過程中。三種情景下，中、大班幼兒有參照估數的精準性均具有顯著的差異，且三種情景下，大班幼兒的有參照估數精準性均高于中班。對不同數量的有參照估數，大班幼兒的精準性也均高于中班。

中、大班之所以在有參照估數精準性方面具有顯著差異，一方面是因為幼兒有參照估數的能力與其數感、數概念和視覺空間認知能力等方面的發展息息相關，伴隨年齡的增長，幼兒各方面及整體的數學能力逐漸增強，有參照估數的精準性也因此越來越高。另一方面，已有研究發現，幼兒估數的精準性與有效的估數策略運用之間存在正相關的關系。[36][37]本研究中所列出的“眼球效應”“參考量比較”“分解—重組”“利用數數”均屬于有效的估數策略，估數時大班幼兒運用以上四種估數策略的占比為62.8%，高于中班幼兒的占比52.5%，因此大班比中班表現出較高的有參照估數發展水平。

（二）估數情景對幼兒有參照估數精準性的影響

本研究發現三種情景下幼兒有參照估數精準性的差異不顯著，一方面由于中、大班幼兒均處于以具體形象思維為主的發展階段，還未完成向抽象邏輯思維的過渡，因此在估數時不易受到情景抽象程度這一因素的干擾。另一方面，為了最大限度減少排列方式、待估物體差異等因素對幼兒有參照估數的干擾，本研究的測查工具與已有研究不同，以粘有黑色紐扣的白紙板作為實物呈現情景，以粘有黑色紐扣紙板的照片作為實物圖片呈現情景，以計算機隨機打印的黑色圓點作為數點呈現情景。雖然三者的抽象程度不同，但肉眼感知到的差異并不十分明顯，這也是導致三種情景下幼兒有參照估數精準性差異不顯著的原因之一。

除此之外，本研究還分別對中班和大班三種情景下有參照估數精準性的差異進行分析，發現大班幼兒的有參照估數精準性在三種情景兩兩之間的差異不顯著，中班幼兒的有參照估數精準性在三種情景兩兩之間的差異邊緣顯著，且實物呈現情景總分的均值>實物圖片呈現情景總分的均值>數點呈現情景總分的均值，即估數情景越抽象中班幼兒的有參照估數精準性越低，這符合幼兒思維發展從具體到抽象的特點。

（三）待估數量對幼兒有參照估數精準性的影響

本研究結果顯示，幼兒對數量15、20、35、50的估數精準性差異顯著，隨著待估數量的增大，幼兒有參照估數的精準性遞減，待估數量的大小是影響幼兒有參照估數精準性的重要因素。待估數量與參考量相差的大小也是影響幼兒有參照估數精準性的一個重要因素，待估數量與參考量相差越大，幼兒有參照估數的精準性就越低。這一結果與已有研究結果一致。[38][39]首先，因為隨著待估數量的增大，幼兒所需處理的信息量會隨之增加，進而延長估數的反應時間，由于測查時有回答時間的限制，所以幼兒在短時間內處理較大數量的估計，會比處理較小數量的估計更困難，進而影響了估數的精準度。其次，由于幼兒對小數量的感知經驗比對大數量的感知經驗更豐富，對小數量的感知能力也比對大數量的感知能力更強。最后，由于本研究提供的參考量是10，待估數量15、20、35、50與參考量的接近程度依次越來越低，因此幼兒將待估數量與參考量進行對比時，兩者相差越小，越利于幼兒根據參考量進行估數，估數的精準性也就越高。

本研究在探究幼兒對數量15、20、35、50有參照估數精準性的兩兩之間的差異時，發現幼兒除了對數量35、50有參照估數精準性的差異不顯著，對其他數量兩兩之間的差異均顯著。一方面是因為數量50雖然比數量35大，與參考量的接近程度也更低，但數量50是參考量10的整倍數，而35不是參考量10的整倍數，在一定程度上會影響幼兒有參照估數的精準性。另一方面，由于數量50和35與其他待估數量相比是較大的數量，且兩者相差不多，不利于幼兒精確分辨兩者之間的差異，因此幼兒表現出的對數量35和50的有參照估數精準性差異不顯著。這說明，數量大到一定程度之后，對估數精確性的影響便不再顯著。

（四）幼兒有參照估數策略運用的特點

已有研究認為估數策略的運用會影響估數的精準性，在策略的選擇方面雖有不同，但通常也具有共性。[40][41][42][43][44]本研究發現大多數幼兒在進行有參照估數時運用“參考量比較”“不知道”“其他”“眼球效應”的策略，較少有幼兒運用“分解—重組”和“利用數數”的策略。一方面是因為“分解—重組”策略的運用需要幼兒具備較強的“分與合”“整體與部分”等相關數學能力和經驗，是一種較難的策略。另一方面，“利用數數”所涉及的點數能力雖然中班和大班幼兒已能夠熟練掌握，但在測查時主試為了強調任務是“估數”而不是“數數”，會說“請你不要數，來看看這里有多少”，這在一定程度上會降低幼兒運用“利用數數”的策略的可能性。

本研究還發現幼兒有參照估數合理時，大多運用的是“參考量比較”策略，而當幼兒不明確或無法說出估數策略時，估數的準確率也隨之下降。由于“參考量比較”策略需要幼兒在理解什么是參考量的基礎上，利用參考量與待估數量進行對比來完成估數，所以這是一種較有效的估數策略，能夠在一定程度上幫助幼兒精準估數。另外，幼兒在進行有參照估數時更善于將與參考量接近的待估數量與參考量進行對比，本研究為幼兒提供的參考量是10，待估數量15、20、35、50與參考量相差依次越來越多，研究結果顯示幼兒對參考量的運用也越來越少。這說明待估數量與參考量差額的大與小，是影響幼兒有參照估數時是否運用參考量進行比較的關鍵因素。

五、教育建議

（一）引導幼兒認識到估數是一種解決日常生活問題的有效辦法

數學因其結構的邏輯性、推理的嚴謹性和結論的精準性，作為一種技能在日常生活中被廣泛運用，但數學在生活中的運用并不總是力爭要得到一個精確的答案。很多時候我們面對大量的數和量方面的信息，短時間內無法快速給出一個精確的答案或無須精準計數時，可以通過估數對其進行模糊的、近似的處理。因此，引導幼兒認識到估數是一種解決日常生活問題的有效辦法至關重要。例如，天空中有成群的鳥兒快速飛過，我們想知道鳥兒的數量卻沒辦法數清楚時;到池塘邊看魚，想知道大概有多少條魚卻無法進行一一點數時。教師和家長都可以引導幼兒通過估數來解決這些問題，進而讓幼兒認識到估數是解決日常生活中遇到的各種各樣數學問題的有效方法之一。

（二）引導幼兒在日常生活中積累估數的相關經驗

本研究發現，幼兒在進行估數時經常會聯系到日常生活中的一些經驗，例如“這些糖果好像和昨天那些豆子一樣多”。估數源于生活，應該在生活中積累經驗，再運用于生活之中。家長和教師是幼兒重要的教育者和引導者，幼兒估數經驗的積累不僅可以在幼兒園的教學活動中進行，更需要在幼兒園及家庭的日常生活中進行。因此，建議教師和家長在了解幼兒估數經驗的基礎上，利用生活中常見的事和物為幼兒創設熟悉的估數情景，例如“猜猜看我們家的鞋柜里大概有多少雙鞋？”“今天班級里大概來了多少客人老師？”幫助幼兒在日常生活中積累估數經驗，進而不斷提高估數能力和問題解決能力。

（三）開展多樣的具有年齡適宜性的估數活動

本研究發現，不同年齡階段的幼兒具有不同水平的有參照估數能力。中班幼兒處于估數能力發展的起步階段，多數能夠合理完成對數量15的有參照估數，少數能夠合理完成對數量20、35和50的有參照估數，對估數概念和應用場景的理解還不完整。大班幼兒的有參照估數水平高于中班幼兒，大多數處于“合理估計”的水平，能夠合理完成對數量15和20的有參照估數，少部分幼兒能夠合理完成對數量35和50的有參照估數。因此，教師和家長在與幼兒進行相關互動時可以從小數量入手，引導幼兒先理解估數的定義和意義，在此基礎上為幼兒提供多樣的、豐富的估數情景和動手操作的材料，并逐步提高估數游戲的難度。

（四）鼓勵幼兒關注參考量和分享估數策略

估數并不是沒有規律地胡亂猜測，需要運用相應的估數策略。本研究發現，有效的估數策略能夠提高估數的精準性，隨著估計者年齡的增長，估數策略的選擇也隨之發生改變。參考量的提供能夠豐富幼兒估數策略的選擇和運用，進而影響估數能力的發展，少數的中班幼兒表現出對參照量的初步利用和把握，超過一半的大班幼兒能夠運用參考量進行估數。因此，教師和家長日常與幼兒進行估數相關的互動時，可以引導其關注參考量，鼓勵幼兒分享所運用的估數策略，進而提高合理估數的能力。例如：“你剛才是根據這個盒子里的15個橘子來猜這個筐里橘子的數量嗎？可以告訴我你具體怎么猜的嗎？”

參考文獻：

[1][7]SIEGLER R S， BOOTH J L. Handbook of mathematical cognition：development of numerical estimation[M]. London： Psycholvgy Press，2005：197-212.

[2]HANSON S A， HOGAN T P. Computational estimation skill of college students[J]. Journal for Research in Mathematics Education，2000，31（4）：483-499.

[3]HOGAN T P， BREZINSKI K L. Quantitative estimation： one， two， or three abilities？[J]. Mathematical Thinking and Learning，2003，5（4）：259-280.

[4]MONTAGUE M， VAN GARDEREN D. A cross？鄄sectional study of mathematics achievement， estimation skills，and academic self-perception in students of varying ability[J]. Journal of Learning Disabilities，2003，36（5）：437-448.

[5]BRIGHT G W. Estimation as part of learning to measure[J]. National Council of Teachers of Mathematics

Yearbook，1976，38：87-104.

[6]DOWKER A. Computational estimation strategies of professional mathematicians[J]. Journal for Research in Mathematics Education，1992，23（1）：45-55.

[8][21]徐繼紅，司繼偉，周新林，等.數量估計的研究回顧[J].心理科學，2010，33（3）：646-648.

[9][25][28][37]趙振國.3～6歲兒童估算和數感的發展研究[D].上海：華東師范大學，2006：28-31.

[10]SOWDER J T. Handbook of research on mathematics teaching and learning： estimation and number sense[M]. New York： Macmillan，1992：371-389.

[11]馬忠林.日本中小學數學課程新方案介紹[J].課程·教材·教法，1989（01）：59-60.

[12]沈蘭.關于制訂課程標準的建議：兼評《加拿大安省數學課程標準（1～9年級）》[J].外國教育資料，2000（05）：21-24.

[13]孫曉天.荷蘭的數學教育和數學課程標準[J].教育科學研究，2000（03）：85-91.

[14]DEHAENE S， COHEN L. Towards an anatomical and functional model of number processing[J]. Mathematical Cognition，1995（01）：83-120.

[15]HUNTLEY-FENNER G. Childrens understanding of number is similar to adults and rats： numerical estimation by 5-7-year-olds[J]. Cognition，2001，78（3）：B27-B40.

[16]SIEGLER R S， BOOTH J L. Development of numerical estimation in young children[J]. Child Development，2004，75（2）：428-444.

[17][23][26][29]趙振國.3～6歲兒童數量估算、數數能力及視覺空間認知能力發展關系的研究[D].上海：華東師范大學，2009：81-112.

[18]SIEGLER R S， OPFER J E. The development of numerical estimation： evidence for multiple representations of numerical quantity[J]. Psychological Science，2003，14（3）：237-250.

[19]BOOTH J L， SIEGLER R S. Developmental and individual differences in pure numerical estimation[J].DevelopmentalPsychology，2006，42（1）：189-201.

[20]OPFER J E， DE VRIES J M. Representational change and magnitude estimation： why young children can make more accurate salary comparisons than adults[J]. Cognition，2008，108（3）：843-849.

[22]臧蓓蕾，張俊.基于潛在類別分析的方法探究3～5歲兒童心理數線發展的特點[J].學前教育研究，2017（07）：49-60.

[24][27]張芳.不同錨定方式下小學生數量估計的特點[D].開封：河南大學，2011：19-29.

[30]CRITES T. Skilled and less skilled estimators strategies for estimating discrete quantities[J]. The Elementary School Journal，1992，92（5）：601-619.

[31][40]SIEGEL A W， GOLDSMITH L T， MADSON C R. Skill in estimation problems of extent and numerosity[J]. Journal for Research in Mathematics Education，1982，13（3）：211-232.

[32]LUWEL K， LEMAIRE P， VERSCHAFFEL L. Childrens strategies in numerosity judgment[J].Cognitive Development，2005，20（3）：448-471.

[33]LEMAIRE P， LECACHEUR M. Aging and numerosity estimation[J]. The Journals of Gerontology Series B： Psychological Sciences and Social Sciences，2007，62（6）：305-312.

[34]司繼偉，孟麗麗，徐繼紅.測量估計研究：回顧與展望[J].心理科學，2007（06）：1466-1468.

[35]韓瑽瑽，陳蒲晶，陳英和.兒童數概念發展的影響因素：表面相似性效應與標簽效應[J].心理發展與教育，2010，26（5）：449-456.

[36]LEVINE D R. Strategy use and estimation ability of college students[J]. Journal for Research in Mathematics Education，1982，13（5）：350-359.

[38]BAROODY A J， GATZKE M R. The estimation of set size by potentially gifted kindergarten-age children[J]. Journal for Research in Mathematics Education，1991，22（1）：59-68.

[39]PORTLEY M， DURGIN F H. The second number？鄄estimation elbow： are visual numbers greater than 20 evaluated differently？[J]. Attention，Perception & Psychophysics，2019，81（5）：1512-1521.

[41]MARKOVITS Z， HERSHKOWITZ R. Relative and absolute thinking in visual estimation processes[J]. Educational Studies in Mathematics，1997，32（1）：29-47.

[42]VERSCHAFFEL L， DE CORTE E， LAMOTE C， et al. The acquisition and use of an adaptive strategy for estimating numerosity[J]. European Journal of Psychology of Education，1998，13（3）：347-370.

[43]GANDINI D， LEMAIRE P， ANTON J L， et al. Neural correlates of approximate quantification strategies in young and older adults： an fMRI study[J]. Brain Research，2008，1246：144-157.

[44]ANOBILE G， CASTALDI E， MOSCOSO P A M， et al. “Groupitizing”： a strategy for numerosity estimation[J]. Scientific Reports，2020，10（1）：1-9.

Abstract： Numerosity estimation is an important part of mathematical concepts. The study selected 111 children from K2 and K3 classes in a kindergarten in Nanjing to investigate the development characteristics of reference numerosity estimation of 4～6 years old children. Results showed that K3 children outperform K2 children significantly. The size of quantity significantly affects both ages： they perform at lower level with the quantity increased. The abstraction of situation has no significant effect on the accuracy of reference numerosity estimation while estimation strategies used by children have. Children using “benchmark comparison” are likely to get better results， but children who could not tell correctly their strategy often estimate wrong. Children tend to use “benchmark comparison” strategy when the size of estimated number is closer to reference number. Adults should guide children to realize that numerosity estimation is an effective way to solve problems in daily life. Children should start with small quantity in developmental appropriate activities organized by adults for them， and be encouraged to share their estimation strategies.

Key words： 4～6 years old children， numerosity estimation， reference numerosity estimation， numerosity estimation strategy