壓氣機葉輪失效轉速預測方法研究

景國璽，張文凱，張軍海，劉欣源，花琳

(1.河北工業大學機械工程學院，天津 300401；2.天津市新能源汽車動力傳動與安全技術重點實驗室，天津 300400；3.中國北方發動機研究所(天津)柴油機增壓技術重點實驗室，天津 300400)

為滿足日益嚴格的環保要求和高功率要求，渦輪增壓技術在20世紀被首次提出。渦輪增壓技術可以大幅度提高內燃機的性能，減少有害氣體的排放，對提高內燃機的性能意義重大[1]。由于汽車運行工況復雜多變，增壓器轉速有時會超過標定轉速，而且高功率柴油機要求不斷提高增壓比，這些都對增壓器的渦輪和葉輪的強度及疲勞性能提出更高的要求，而渦輪和葉輪的工作可靠性是增壓器設計的難點[2]。

在實際工作過程中渦輪和葉輪受到多種載荷的耦合作用，包括螺栓裝配載荷、熱載荷、離心力載荷和氣動載荷，其中離心力載荷對渦輪和葉輪的應力及變形影響最大[3-4]。北方交通大學的朱寶山和侯炳麟等[5]針對增壓器超轉速下的葉輪進行彈塑性分析，為超轉速加工工藝規程提供了定量依據。浙江大學的陸君毅和吳秀仁[6]通過葉輪的超轉速破壞性試驗，對高強度鋼制閉式葉輪在離心力場下的破壞過程進行了試驗研究。浙江大學的吳秀仁[7]提出了一種模塊式增壓器葉輪立式超轉速試驗機，具有試驗轉速、質量、外形尺寸等參數范圍寬的特點，理論上最高轉速可達120 000 r/min。中航工業發動機設計研究所的萬江艷和周柏卓[8]建立了與材料延伸率相關的輪盤彈塑性破裂準則，采用非線性有限元法對變厚度輪盤破裂試驗件的破裂轉速進行了預測，試驗對比效果良好。王浩然[9]進一步使用 Tresca 屈服準則下的整體塑性失穩破壞準則，準確預測了 GH4169 材料復雜幾何形狀模擬盤的破裂轉速，揭示了整體塑性失穩破壞準則下屈服準則的選用對于輪盤破裂轉速預測的影響。Hassani等[10]采用了HAM方法和有限元法，得到了彈塑性載荷作用下非均勻厚度和材料特性的旋轉圓盤的應力應變分布。Ranjan和 Vinayak等[11]采用有限元方法對典型變厚度燃氣輪機盤進行了不同轉速下的彈性和彈塑性分析，得到了復雜載荷條件下的爆炸裕度。

目前多數研究都是針對航空發動機渦輪盤進行破裂轉速預測。根據GJB 241A—2010《航空渦輪噴氣和渦輪風扇發動機通用規范》，當輪盤承受最大溫度梯度和最高工作溫度時，輪盤的設計破裂轉速不低于最高允許穩態轉速的122%，但對于車用發動機壓氣機葉輪，葉輪的破裂轉速要求在標定轉速的1.4倍以上。考慮到航空發動機渦輪盤與壓氣機葉輪結構和材料特性的差異，渦輪盤預測破裂轉速的方法不能完全應用于壓氣機葉輪。隨著增壓技術的廣泛應用，壓氣機葉輪在超轉速工況下的安全成為亟待解決的問題，也是影響壓氣機正常工作的關鍵問題之一，對壓氣機葉輪的轉速破壞研究分析具有重要的意義。

本研究針對某型壓氣機葉輪，進行彈塑性失效分析，提出3種預測失效轉速的方法。針對葉輪材料鍛鋁合金2A70進行拉伸試驗，獲得材料的各項性能參數。對壓氣機葉輪進行超轉速破壞試驗，將試驗葉輪失效轉速與仿真模擬預測失效轉速進行對比，驗證3種預測失效轉速方法的準確性。

1 葉輪超轉速理論分析

大量的強度破壞現象和試驗證明，無論應力狀態多么復雜，在常溫、靜載荷的條件下，材料失效的形式主要有兩種，分別為脆性斷裂和塑性屈服[12]。本研究中葉輪材料為鍛鋁合金，在屈服極限之前應力與應變成正比，在屈服極限之后出現塑性變形。選擇合適的強度破壞理論，是預測葉輪最大失效轉速的關鍵。

1.1 Mises應力理論

對于均質脆性材料，第一強度理論與試驗結果吻合，即無論材料處于什么應力狀態，只要危險點處的最大拉應力σ1達到材料單向拉伸時的斷裂真應力σ，材料就會發生脆性斷裂，即材料的破壞條件為

σ1=σ。

(1)

對于復雜構件來說，該理論未考慮其他兩個主應力的影響，因此德國的R. Von Mises 在 1931 年提出Mises應力。該應力考慮中間應力的影響，不需要知道3個主應力的方向。對于韌性金屬，該條件非常接近于試驗情況。Mises應力計算公式為

(2)

式中：σx，σy和σz為3個方向的正應力；τxy，τyz和τzx為3個方向的剪應力。

1.2 主塑性應變理論

對于脆性斷裂來說，第二強度理論與試驗吻合較好，即無論材料處于什么應力狀態，只要危險點處的最大拉應變ε1達到材料的單向拉伸斷裂時的拉應變極限值ε1u，材料就發生脆性斷裂，即材料破壞條件為

ε1=ε1u。

(3)

對于受力情況復雜的構件來說，應變可分為彈性應變和塑性應變，彈性應變在應力消失后可恢復[13]，因此提出主塑性應變理論：當葉輪的轉速增加時，葉輪任一點的主塑性應變εp1達到材料的斷裂塑性應變εp時，葉輪發生破壞，這時的轉速就是葉輪的失效轉速。

1.3 等效塑性應變能理論

超轉速過程中任一點的應變ε都可表示為彈性應變εe和塑性應變εp之和，即

(4)

式中：E為彈性模量；K為強度系數；n為應變強化指數。葉輪超轉速的過程中應力應變關系符合著名的Remberg-Osgood彈塑性模型。若變形過程中不考慮其他能量對該系統的影響，外力的變化緩慢，則結構中的應變能近似等于外力對該系統做的功，即應力應變曲線下包含的面積可用下式表示[14]：

(5)

式中：ε為應變；σ(ε)為應力關于應變的函數。

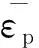
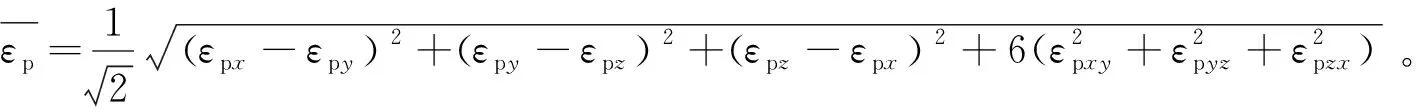
(6)

式中：εpx，εpy和εpz為3個方向的塑性正應變；εpxy，εpyz和εpzx為3個方向的塑性剪應變。

(7)

式中：εp為塑性應變；σ(εp)為應力關于塑性應變的函數。

2 葉輪超轉速破壞仿真模擬研究

2.1 有限元模型

壓氣機模型(見圖1)由螺母、葉輪、軸封套、甩油盤、止推、間隔套和轉軸組成，壓氣機葉輪、軸承套等零部件通過螺母與轉軸固定。模型采用四面體二階單元，局部進行細化處理，葉輪材料為鍛鋁合金2A70。

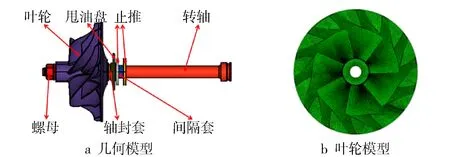
圖1 壓氣機模型

2.2 葉輪材料的力學性能參數

葉輪在工作過程中的受力情況十分復雜，對葉輪的強度等性能提出了很高的要求。考慮到葉輪在超轉速過程中發生塑性變形，僅采用彈性模型得出的結果并不可靠，無法做出確切的失效分析，其結果將使模型不能充分發揮材料的全部承載能力[15]，因此采用彈塑性模型。根據GB/T 228.1—2010《金屬材料 拉伸試驗 第1部分：室溫試驗方法》進行葉輪試樣的室溫拉伸試驗，拉伸試樣尺寸如圖2所示，試驗在MTS電子萬能試驗機上進行。測試試樣(見圖3)為3個，試樣編號為W1-L-1，W1-L-2，W1-L-3。試驗溫度為25 ℃，試驗時加載應變速率為0.000 25/s。

圖2 拉伸試樣尺寸

圖3 室溫拉伸試驗試樣

圖4示出2A70材料的工程應力應變曲線，可以看出，拉伸變形后期存在輕微頸縮現象，導致在工程應力應變曲線中出現應力下降的情況。材料在屈服點以后，分子的流動導致試樣的橫截面面積A顯著減小，材料實際承受的應力要大于按原始的橫截面面積計算的工程應力。所加載荷應等于真實應力與實際面積的乘積。經過數據處理，得到真實應力應變曲線，如圖5所示。室溫下葉輪材料2A70的性能參數見表1。

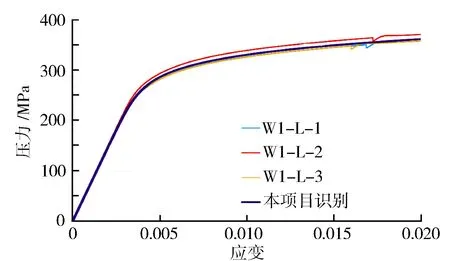
圖5 2A70材料真應力應變曲線

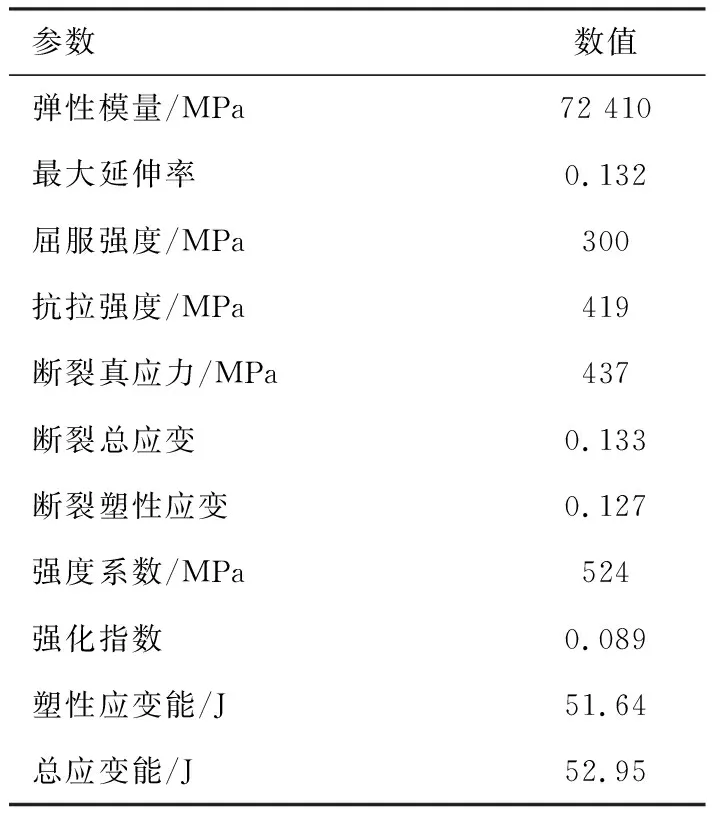
表1 2A70材料參數

2.3 葉輪載荷分析和約束條件

參考葉輪在超轉速試驗的工作過程，葉輪主要受到螺栓預緊力和離心力的作用。根據螺母的形狀尺寸以及扭緊力矩62 N·m，可計算出離心力約為38 000 N。離心力載荷以角速度的形式施加在葉輪上，隨著轉速的增加，離心力不斷增大，角速度也不斷增大。轉速的變化過程按照葉輪超轉速破壞試驗規范進行，如圖6所示。

圖6 葉輪升速規范

根據葉輪的超轉速試驗進行約束，如圖7和圖8所示，對位置1約束Z方向的移動，對位置2約束X和Y方向的移動，對位置3施加螺栓預緊力。

圖7 壓氣機約束位置

圖8 壓氣機螺栓預緊面

2.4 葉輪載荷特性分析

利用abaqus軟件，進行壓氣機葉輪的有限元分析。在仿真分析計算超轉速工況時，首先需要施加螺栓預緊載荷，僅考慮螺栓裝配載荷時的應力分布云圖如圖9所示。Mises應力為葉輪的等效應力，主應力圖可用來判斷局部的拉伸壓縮情況。當主應力為正時，呈拉伸狀態，當主應力為負時，呈壓縮狀態。

葉輪主要受壓應力，最大壓應力為269 MPa左右，出現在葉輪靠近螺母一端的端面上，是由于螺栓預緊力在此處存在應力集中現象，但葉輪未發生塑性變形。

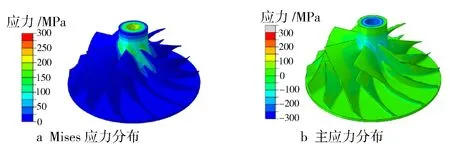
圖9 螺栓預緊力載荷下的應力分布

圖10示出不同轉速下葉輪的Mises應力分布云圖，圖11示出不同轉速下葉輪的主應力分布云圖，可以看出，在標定轉速90 200 r/min下，葉輪的最大拉應力為327 MPa左右，出現在葉片根部區域。葉片工作面的葉根處主要受拉應力，另一側葉根處主要承受壓應力。由于葉片根部設計相對較薄，因此出現高應力區[16]。

圖10 不同轉速下葉輪Mises應力分布

圖11 不同轉速下葉輪主應力分布

3 葉輪超轉速破壞試驗

3.1 試驗說明

渦輪增壓器葉輪超轉速破壞試驗的目的在于評估增壓器在超轉速條件下的工作可靠性，同時可作為確定增壓器最高破壞轉速的依據。在結構設計不變的前提下，葉輪超轉速破壞試驗結果反映葉輪承受離心力的能力。大量的工程實踐證明，利用葉輪的超轉速破壞試驗可以檢查葉輪設計的可靠性和鑄造質量，對葉輪的設計和應用都具有重要的意義。

增壓器的超轉速破壞試驗采用外氣源熱吹的方式進行，在有防護裝置的專用試驗臺架(見圖12)上進行。在試驗開始時，葉輪加速到標定轉速，穩定運行5～20 min，然后繼續增加葉輪的轉速，直到葉輪發生斷裂破壞，記錄葉輪發生失效的轉速，為增壓器壓氣機葉輪的仿真模擬提供最大轉速依據。

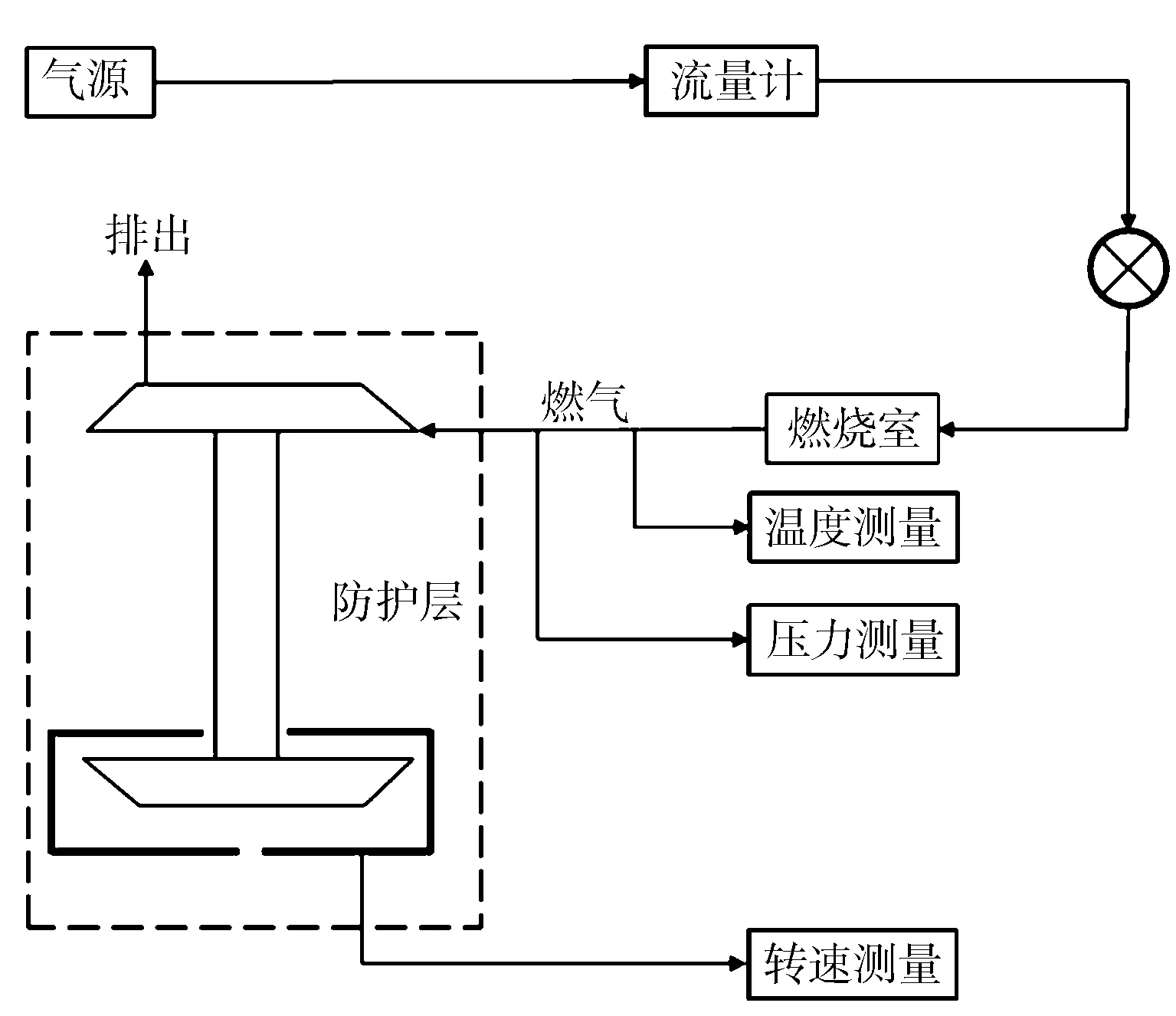
圖12 葉輪超轉速試驗臺示意

3.2 葉輪的超轉速破壞試驗結果分析

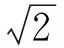
在超轉速試驗臺上完成葉輪的超轉速試驗，當壓氣機葉輪飛散時，實際轉速約為126 700 r/min，約為標定轉速的1.4倍，滿足基本設計要求。

4 葉輪失效轉速預測方法

在葉輪轉速增加時，葉輪內部的缺陷或者葉輪表面的加工問題，都會造成應力集中并產生裂紋源。在試驗時，葉輪裂紋拓展，直至斷裂。但在仿真時，采用不同的葉輪失效轉速預測方法，往往會得出不同的結果。

本研究采用了3種預測失效轉速的方法，分別基于葉輪的Mises應力、主塑性應變和等效塑性應變能。方法一基于葉輪的Mises應力，比較通過拉伸試驗得到的材料斷裂真應力與葉輪仿真模擬得到的Mises應力，找出葉輪的失效轉速。方法二基于主塑性應變，為試驗試樣斷裂時發生的主塑性應變。方法三基于等效塑性應變能，即物體變形過程中儲存在物體內部的勢能。根據超轉速試驗易開裂的位置，結合有限元仿真的結果，在葉輪上確定14個典型的觀察點，各觀察點的位置如圖13所示。由于葉輪是軸對稱模型，因此選擇的觀察點集中于一對大、小葉片和輪盤上，根據Mises應力、主塑性應變出現的位置和結構特征來確定。

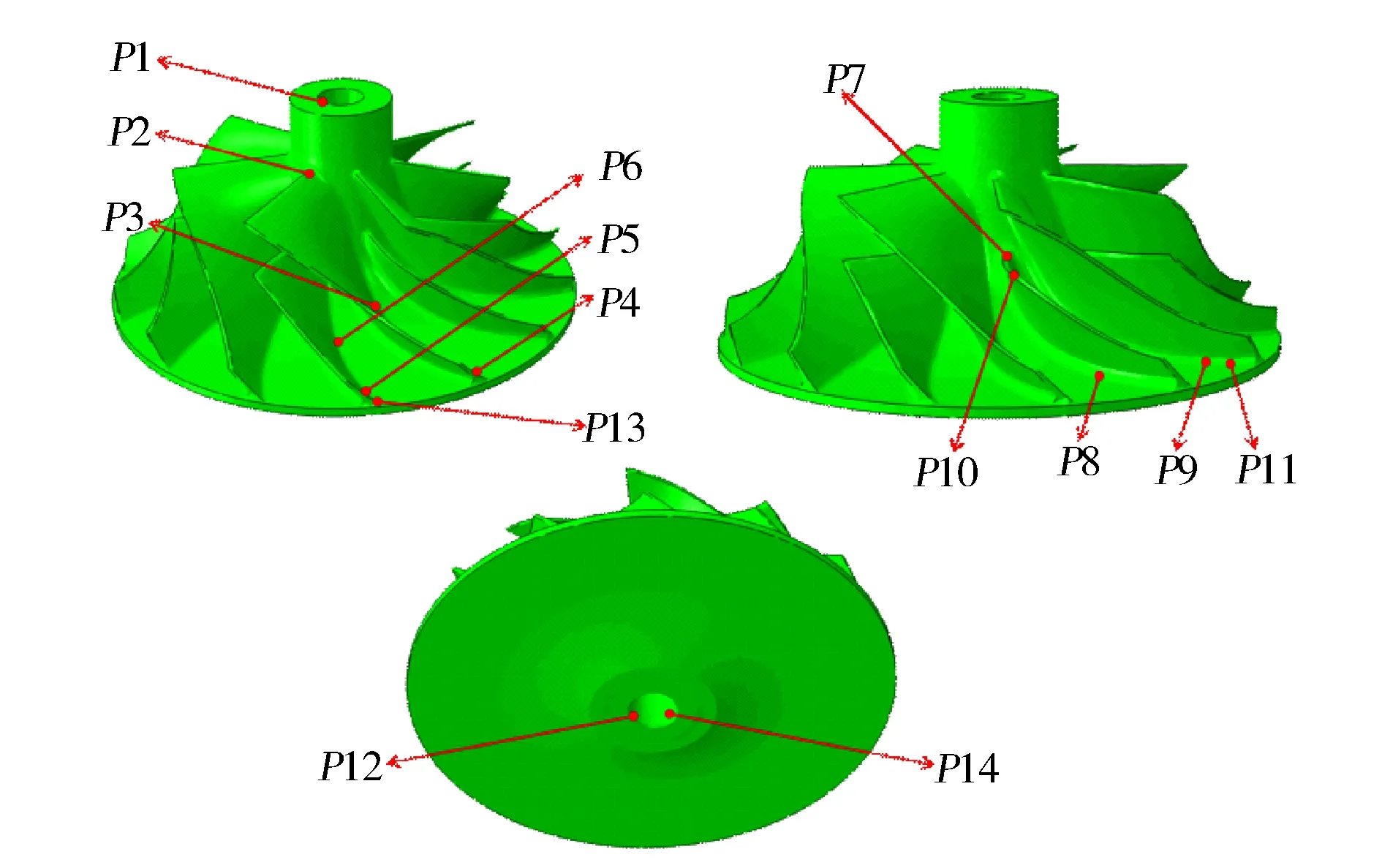
圖13 觀察點示意

4.1 基于Mises應力的失效轉速預測方法

通過材料的拉伸壓縮試驗，可以得出材料在室溫下的斷裂真應力為437 MPa。根據Mises應力理論，當葉輪上任一點的Mises應力大于437 MPa時，葉輪發生破壞，此時對應的葉輪轉速即為葉輪失效轉速。由圖14可知，葉輪上P5點的Mises應力首先達到437 MPa，開裂位置出現在小葉片葉根處。此時葉輪的轉速131 975 r/min即為失效轉速，是標定轉速的1.46倍。

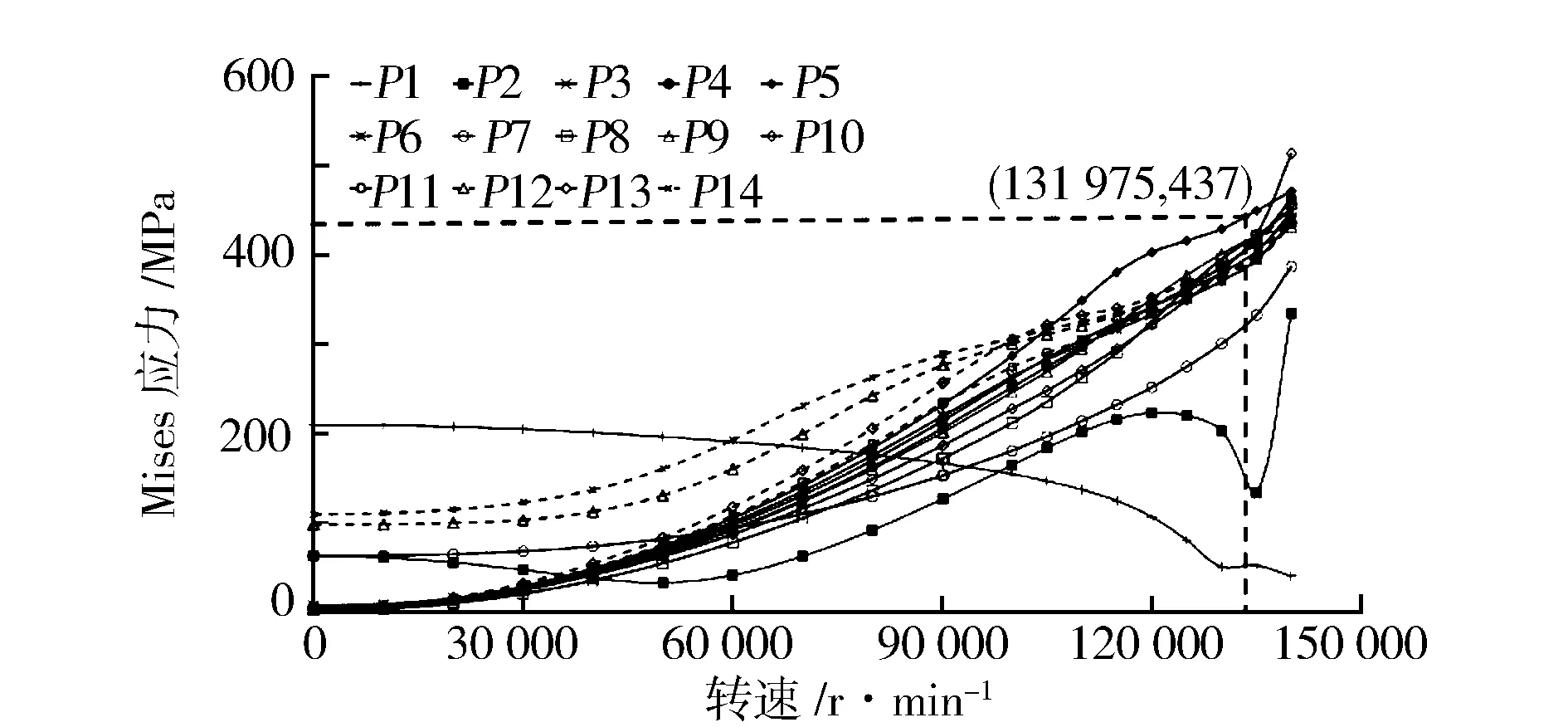
圖14 不同觀察點Mises應力隨轉速的變化曲線

4.2 基于主塑性應變的失效轉速預測方法

通過材料的拉伸壓縮試驗，可以得出材料在室溫下的斷裂塑性應變為0.127。根據主塑性應變理論，當葉輪上任一點的主塑性應變大于0.127時，葉輪發生破壞。由圖15可知，葉輪上P13點的主塑性應變首先達到0.127，開裂位置出現在小葉片葉根處。此時葉輪的轉速137 815 r/min即為葉輪的失效轉速，約為標定轉速的1.53倍。

圖15 不同觀察點主塑性應變隨轉速變化曲線

4.3 基于等效塑性應變能的失效轉速預測方法

通過材料的拉伸試驗，可以得出在室溫下材料破壞時的塑性應變能為51.64 J。根據葉輪超轉速過程中的等效塑性應變能理論，當葉輪任一點的等效塑性應變能大于51.64 J時，葉輪發生破壞。由圖16可知，葉輪上P13點的等效塑性應變能首先達到材料破壞時的塑性應變能，開裂位置出現在小葉片葉根處。此時葉輪的轉速為135 455 r/min，即135 455 r/min為失效轉速，約為標定轉速的1.5倍。

圖16 不同觀察點等效塑性應變能隨轉速的變化

4.4 葉輪失效轉速預測方法分析

經過試驗驗證與仿真的對比分析可知，利用Mises應力預測失效轉速的方法相對試驗偏差相對較小，為4.2%，Mises應力值可從仿真中直接得到。利用等效塑性應變能計算預測失效轉速的方法偏差相對較大，為6.9%。利用主塑性應變預測失效轉速的方法相對試驗偏差最大，為8.8%，可從仿真結果中直接讀取。

從對比結果來看，三種方法預測出的失效轉速均大于試驗值。出現這種現象的原因有兩個：一是葉輪表面存在用于改善葉輪氣動性能的紋路，葉輪表面較粗糙，而葉輪材料拉伸試驗中使用的拉伸試樣較光滑，這是仿真得出的葉輪失效轉速大于試驗值的主要原因；二是由于試驗成本的限制，只進行了一個葉輪的超轉速試驗，超轉速試驗得出的失效轉速具有一定的分散性，試驗失效轉速結果理論上應為一定范圍區間的分布，因此仿真給出的失效轉速與試驗值存在一定的偏差。

本研究采用的3種方法借鑒了航空發動機渦輪盤的破裂準則，并在此基礎上進行深入研究。從預測結果來看，3種方法同樣適用于車用發動機壓氣機葉輪的失效轉速預測，因此模型具有一定的普適性，但對于塑性較好的鋁合金材料，推薦采用Mises應力作為超轉速失效判據。

5 結論

a) 葉輪在超轉速工況下主要受到螺栓預緊力和離心力的影響，其中離心力的影響最大；最大應力出現在葉片根部區域；

b) 在超轉速試驗臺完成壓氣機葉輪的超轉速試驗，葉輪的破壞轉速為126 700 r/min，為標定轉速的1.4倍，符合葉輪強度的安全標準；

c) 提出3種預測葉輪失效轉速的方法，分別基于Mises應力、主塑性應變和等效塑性應變能，綜合比較3種方法，基于Mises應力預測失效轉速的方法相對試驗偏差最小，為4.2%；3種方法預測的破壞位置均在小葉片葉根處，預測的最大轉速均偏大。