高壓氫氣儲運設施泄漏噴射火過程預測模型及其驗證

王振華，蔣軍成，尤飛，李剛，莊陳浩，趙耀鵬，倪磊，潘勇，李丹

（1南京工業大學安全科學與工程學院，江蘇南京210009；2南京工業大學火災與消防工程研究所，江蘇南京210009；3常州大學環境與安全工程學院，江蘇常州213164）

引 言

隨著全球化石能源日益消耗，能源供應日趨緊張，積極探索新能源來取代不可再生的傳統化石能源已經成為趨勢[1]。氫能作為一種清潔高效的新能源，因其燃燒熱值高、清潔無污染、來源廣泛、儲運方便、利用形式多樣等優點，被認為是未來最具吸引力和發展前景的新能源。當前美國、日本、德國等發達國家均已將氫能規劃上升到國家戰略層面，并制定相關政策扶持“氫經濟”發展[2]。經過多年積累，我國氫能產業也正在進入快速發展階段，2020年我國氫氣產量超2000萬噸。據相關資料統計[3]，到2030年，氫能產業將成為我國新的經濟增長點和新能源戰略的重要組成部分，產業產值將突破10000億元，加氫站數量達到1000座，燃料電池車輛保有量達到200萬輛，高壓氫氣長輸管道建設里程達到3000 km，氫能產業基礎設施技術標準體系完善程度接近發達國家水平。目前，我國政府已相繼出臺一系列促進氫能產業加快發展的政策措施，例如，在“十三五”期間，國家先后發布《能源技術革命創新行動計劃（2016—2030年）》《“十三五”國家戰略性新興產業發展規劃》等多項國家綱領性規劃文件，均明確提出將“氫能與燃料電池”作為戰略重點。2019年3月，氫能首次寫入國務院《政府工作報告》，明確將推動加氫等設施建設。2020年4月，國家能源局發布《中華人民共和國能源法（征求意見稿）》，氫能更是被列入能源范疇，這是中國第一次從法律上確認氫能屬于能源。

由于氫氣密度極低，在標準狀況下僅為0.089 g/L，因此發展高效的儲存技術是提高氫能利用效率的關鍵環節，且貫穿于整個氫能產業鏈[4]。根據氫在儲存時所處狀態的不同，可分為氣態儲氫、液態儲氫和固態儲氫，其中高壓氣態儲氫是目前最常用、最成熟和最節能高效的方式[5]。然而，基于氫氣本身的危險特性[如燃燒范圍寬（4.1%~74.1%）、最小點火能低（0.02 mJ）以及在空氣中燃燒速度快等]，加之高壓這一突出的風險要素，因此高壓氫氣一旦發生泄漏和擴散，極易引發火災和爆炸等惡性事故。其中氫噴射火災是一種較為常見的災害類型[6-7]，其產生的強烈熱輻射往往會引發多米諾連鎖反應（Domino chain reaction），引發二次甚至更高次的事故，造成巨大的經濟損失和嚴重的人員傷亡，社會影響十分惡劣。例如，2019年9月，韓國一化工廠發生氫氣泄漏火災事故，導致3名工人燒傷，而在此之前，韓國已發生多起涉氫事故，使得韓國民眾集體抗議反對在其居住地附近修建氫能相關設施。因此，重點研究高壓氫氣儲運設施泄漏過程及其引發噴射火熱輻射危害，并在此基礎上建立相應的預測模型，快速準確地計算出氫噴射火特性參數（如火焰幾何尺寸、輻射熱通量等），就顯得十分迫切而且重要。

近年來國內外學者對高壓氫氣泄漏過程、泄漏后被點燃形成噴射火特性等開展了一系列研究工作。關于高壓氫氣泄漏方面，根據氫氣泄漏源與周圍環境壓力的比值，泄漏氣流可分為亞聲速射流和欠膨脹射流/塞流[8]。對于后者，氣流在泄漏出口處速度等于當地聲速，但其壓力高于周圍環境壓力（欠膨脹），因此氣流在離開泄漏出口后將繼續膨脹加速，在出口附近形成一個擴張的激波結構；隨后氣流壓力逐漸下降至大氣壓，速度達到當地聲速，此時氣體在泄漏出口下游進一步收斂聚集，形成明顯的馬赫盤（Mach disk）結構[9]。針對這一現象，一些學者通過合理簡化建立適合復雜欠膨脹射流的數學模型，用以描述馬赫盤前后的氣體狀態參數變化。這些模型主要包括Birch模型[10]、Ewan模型[11]和Yüceil模型[12]等，通過引入“虛噴口”假設的概念，結合質量守恒方程、動量守恒方程或能量守恒方程，計算出虛噴口處各有效的物性參數變化。此后部分學者利用氣體狀態方程和等熵過程假設建立高壓氫氣泄漏過程模型，將泄漏出口內外氣體狀態變化聯系起來，實現高壓氫氣泄漏過程特征的整體性描述。例如，Mohamed等[13]應用Beattie-Bridgemam氣體狀態方程推導出泄漏氣流熱力學參數計算公式，根據泄漏氣流等熵膨脹和絕熱流動假設，建立高壓氫氣泄漏模型。Schefer等[9]基于Abel-Nobel氣體狀態方程計算出泄漏氣流出口條件，并與實驗結果進行比較，發現預測數據與實驗值比較吻合。Proust等[14]在進行不同泄漏孔直徑條件下高壓氫氣泄漏實驗時，分別使用理想氣體狀態方程和Abel-Nobel氣體狀態方程對儲罐內氣體密度與壓力變化進行預測，結果表明Abel-Nobel氣體狀態方程的預測結果與實驗值更為接近。李雪芳[8]同樣基于理想氣體狀態方程和Abel-Nobel氣體狀態方程建立高壓氫氣泄漏模型，盡管兩種模型的計算結果相一致，但在高壓情況下，Abel-Nobel氣體狀態方程能更加準確地描述氣體行為。在此基礎上，Zhou等[15]利用van der Waals氣體狀態方程對高壓氫氣/天然氣泄漏行為進行描述，并提出相應的理論框架。Zou等[16]近 期 綜 合 考 察 了Abel-Nobel、van der Waals、Redlich-Kwong、Soave-Redlich-Kwong、Peng-Robinson、Aungier-Redlich-Kwong和Beattie-Bridgeman等7種真實氣體狀態方程在預測高壓氫氣泄漏行為時的預測精度和簡潔性，最后選用Abel-Nobel氣體狀態方程建立起高壓氫氣泄漏模型。

而關于氫噴射火尺寸方面，典型的射流火焰結構通常由火焰推舉和可見火焰長度組成。其中火焰推舉行為，即火焰脫離噴口的現象，是一種非常常見的火焰不穩定行為[17]。目前，針對火焰的推舉行為，學者們提出了諸多理論模型試圖闡明其內在機制，例如Vanquickenborne和van Tiggelen[18]的預混模型、Peters和Williams[19]的層流火焰面模型、Byggst?yl和Magnussen[20]的渦耗散概念模型以及Broadwell等[21]的大尺度混合模型等。這些模型對射流燃燒的理論完善有積極的促進作用，并為火災的防控實踐提供幫助。前人對于射流火焰長度也開展了一些研究工作，如早期的Thornton模型是由Chamberlain[22]在前人研究基礎上，基于（烴類）噴射火焰形狀研究得出的半經驗模型，該模型接受了風洞實驗和現場實驗的檢驗，包括陸地和水面上的大量實驗，應用范圍較為廣泛。Delichatsios[23]通過引入無量綱火焰Froude數Frf對浮力和動量主控范圍內的射流火焰長度變化規律進行分析，并建立了相應的無量綱預測模型，在之后開展的高壓氫氣泄漏實驗中該模型也得到驗證[9]。在此基礎上，Molkov等[7]通過從文獻中提取和分析大量氫噴射火火焰長度實驗數據，基于量綱分析原理，提出了一個新的無量綱模型，該模型將傳統射流火焰控制模式進行進一步擴展，包含了新的動量主控（欠膨脹射流）模式。熱輻射為泄漏形成噴射火災的主要危害形式[24]，因此對于火焰熱輻射的分析也是研究重點之一。目前常用的噴射火熱輻射計算模型包括單點源模型[25]、多點源模型[26]和線源模型[27]等。其中單點源模型是一種最簡單的輻射源結構模型，此模型忽略了火焰形狀變化，常被用于預測遠場輻射熱通量。多點源模型在單點源模型的基礎上進行了改進，考慮了火焰高度，可用于近場輻射熱通量的預測，但在大尺寸噴射火上預測精度還有待驗證。線源模型需要對火焰形狀作出合理的假設并求解火焰輻射力，計算也相對復雜，但與其他預測模型相比預測精度有所提高。隨著科學技術的發展，關于氫噴射火的計算機模擬研究也日益受到關注，例如，Brennan等[28]基于LES（large eddy simulation）方法來模擬高壓下的氫噴射火，并選用混合分數/概率密度函數燃燒模型對湍流和火焰之間相互作用進行了分析，發現在0~20%湍流強度范圍內，對火焰長度和寬度模擬的影響非常有限，但隨著湍流強度進一步增強，模擬不穩定性開始顯現。付佳佳等[29]基于OpenFOAM平臺，采用基于有限速率的渦耗散概念燃燒模型和改進的fvDOM輻射模型，對噴口流速為亞音速范圍內的氫噴射火進行模擬，詳細探討了噴口流速和直徑對氫噴射火特性的影響。Cirrone等[30]最近基于CFD（computational fluid dynamics）技術，嵌入k-ε湍流模型、渦耗散概念燃燒模型與DO（discrete ordinates）輻射模型對90 MPa高壓氫噴射火進行模擬，然后與Proust等[14]的實驗結果進行對比分析，兩者結果獲得較好的一致性。綜上所述，可以看出，前人對于高壓氫氣泄漏過程及其形成噴射火幾何特征與熱輻射分布已經開展了一些研究，但是都相對分散，從整體性角度進行探討的很少，且計算機模擬技術還不夠成熟和完善，多作為實驗研究的輔助手段，模擬結果也具有一定的不確定性。

因此，本文基于經驗公式法，采用串聯耦合的研究思路，將高壓氫氣泄漏流動、噴射燃燒和燃燒火焰對外輻射傳熱這3個過程，從形成發展上的連續性和整體性方面進行綜合考慮，在綜合評述前人理論模型基礎上，通過理論分析與建模，建立了高壓氫氣泄漏噴射火過程預測模型；然后分別模擬計算氫氣從壓力為90 MPaⅣ型儲氣瓶和6 MPa管道中發生泄漏后的瞬態過程以及形成的噴射火焰尺寸和燃燒熱輻射變化；最后，將模擬計算結果與前人的實驗數據進行對比。從實際工程應用的角度來看，該預測模型的建立將有助于根據已知參量[氣源初始壓力（P1,0）和溫度（T1,0）、泄漏氣體體積（V）或質量（m）及泄漏出口直徑（d2）等]，對高壓氫氣泄漏引發的噴射火災害進行快速準確地評估，對于評估氫噴射火危害、氫能安全利用以及制定相應的預防措施具有重要現實意義。

1 高壓氫氣泄漏模型

根據前文所述，為了建立能準確描述高壓氫氣泄漏行為且便于工程應用的數學預測模型，本文同樣采用Abel-Nobel氣體狀態方程對泄漏出口處氣體狀態參數變化進行計算。首先，對Abel-Nobel氣體狀態方程預測精度展開分析，研究氣體壓力、溫度對其預測精度可靠性的影響。圖1比較了根據Abel-Nobel氣體狀態方程所計算的氫氣密度和NIST（National Institute of Standards and Technology）推薦的高精度數據[31]。在計算中考慮的氫氣溫度范圍為250~600 K，壓力范圍為0~90 MPa。從圖中可以看出，Abel-Nobel氣體狀態方程在此溫度和壓力范圍內對氫氣密度的預測精度可控制在1.2%以內，具有較高精度預測能力。目前，出于安全考慮，國內商用氫氣鋼瓶充壓不超過15 MPa，長距離輸送管道壓力范圍為2~10 MPa，長管拖車壓力一般為20 MPa，而車載儲氫瓶主要有35、70 MPa兩種，其中后者已研發成功并小范圍應用，但多數在用或在建加氫站尚處于35 MPa壓力技術水平，已不能滿足車輛對儲氫瓶質量、儲氫量的需求，其進一步提升至70 MPa已成為必然趨勢[32]，因此Abel-Nobel氣體狀態方程適用于當前常用的多種高壓氫氣儲運設施泄漏過程的描述。

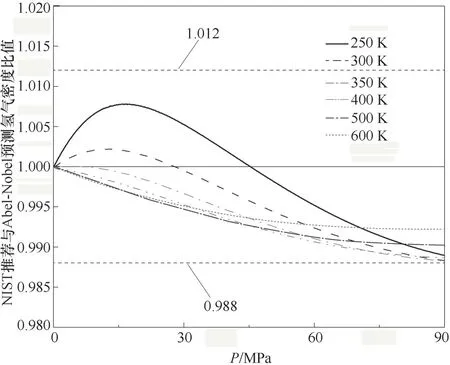
圖1 Abel-Nobel氣體狀態方程以及NIST數據[31]所得的氫氣密度比較（在Abel-Nobel氣體狀態方程中，對于氫氣，b=7.69×10-3 m3/kg）Fig.1 Comparison between predicted densities by using Abel-Nobel EOS and NIST’s recommended data[31]for hydrogen

高壓氫氣儲運系統發生泄漏時的氣體流動如圖2所示。結合Liu等[33]描述的基于Abel-Nobel氣體狀態方程對高壓氫氣泄漏過程中氣體狀態參數變化的計算模型，可以將泄漏過程分為以下兩個部分。

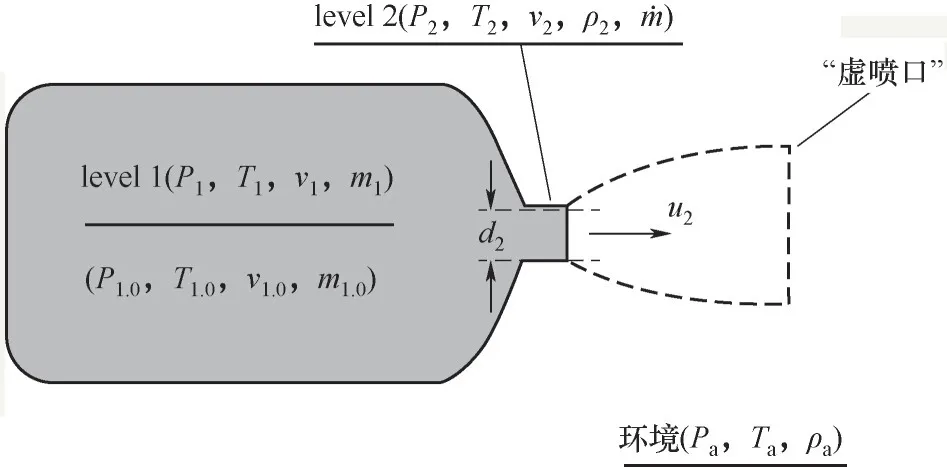
圖2 高壓氣體泄漏過程示意圖Fig.2 Schematic diagram of high-pressure gas leakage process

（1）在泄漏出口處的氣體狀態參數（level 2），包括出口壓力（P2）、比體積（v2）、出口流速（u2）和質量流量（m?）隨泄漏時間變化的方程式可分別表示為：

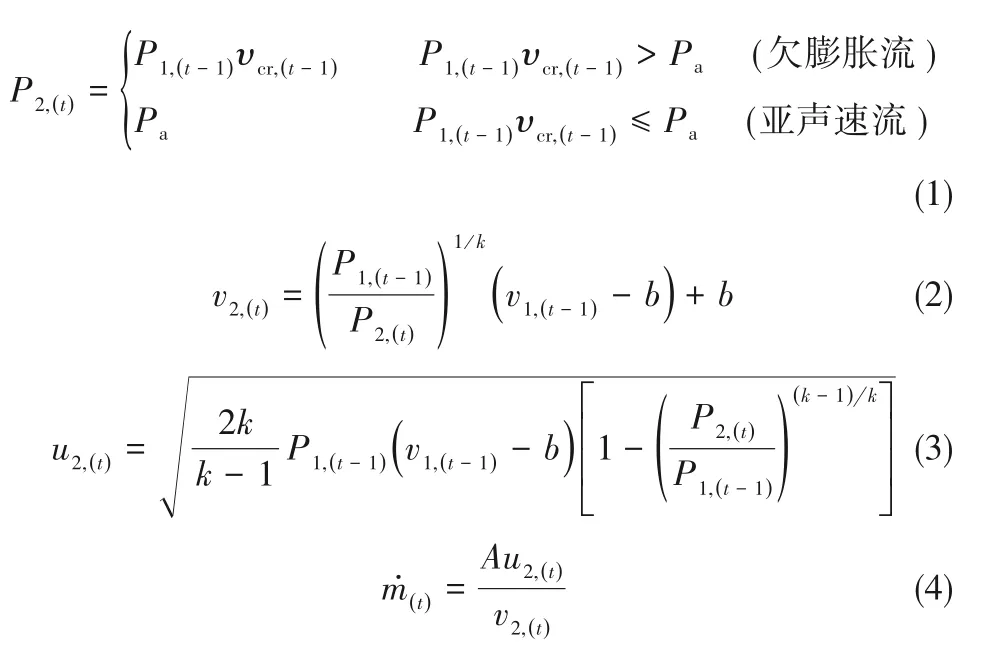
（2）在系統內的氣體狀態變化參數（level 1），包括氣體質量（m1）、比體積（v1）、壓力（P1）和溫度（T1）隨泄漏時間變化的方程式可依次表示為：

2 噴射火尺寸模型

本文主要采用文獻[7]提出的基于Froude數Fr、Reynolds數Re和Mach數Ma綜合影響下的氫噴射火尺寸無量綱關聯式。通過建立一個氫噴射火火焰長度數據集，數據范圍包括：氣源壓力0.1~90.0 MPa，氣源溫度80~300 K，泄漏直徑0.4~51.7 mm，Molkov等[7]發現當數據集中包含較多的欠膨脹氫氣射流火焰長度數據時，基于火焰Froude數的噴射火火焰長度預測模型不能準確描述欠膨脹氫氣射流火焰長度的實際情況，實驗數據分布較為分散。針對這一局限性，他們應用量綱分析方法分析了氫噴射火火焰長度與高壓泄漏過程中實際泄漏出口處主要影響參數的關系，并提出了一種新的無量綱模型，其具體表達式如下：

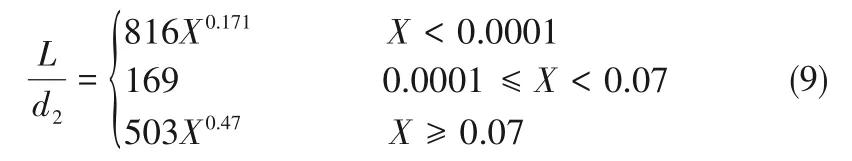
需要指出的是，式（9）為改進后的模型，即通過數據最佳擬合方法，給出其在已發表文獻的氫噴射火火焰長度數據上的最佳擬合方程[34]。可以看出，此模型在對氫噴射火火焰長度預測過程中更加簡便易行，即預測時僅需要確定實際泄漏出口處的狀態（出口直徑d2）和氣體參數變化（出口處氣體流速u2和密度ρ2）以及當地聲速等，而不必考慮欠膨脹條件下的虛噴口模型。另外，該預測模型也將傳統的射流火焰控制模式（浮力主控-過渡-動量主控）進一步發展為包含傳統浮力主控-傳統動量主控（“飽和”膨脹射流）-新的動量主控（欠膨脹射流）模式下的全局氫氣射流火焰長度控制模型。

針對射流火焰的推舉行為，這里將采用Peters等[19]建立的基于應變速率（strain rate）的推舉高度半經驗關聯式，因其在工程上的簡單易用性，其他一些學者在后續研究中進一步證實該預測模型的正確性和有效性[35-36]，該關聯式如下：

式中，C為經驗常數，其值通常隨燃料種類不同而變化（對于氫氣，C=2.65×10-5s）[33]。最后，上述火焰長度（L）和推舉高度（S）兩者之和為氫噴射火總長度（H）。

3 火焰熱輻射計算

火焰的輻射分數xr，一般定義為火焰的總輻射能量與熱釋放速率之比，是火焰熱輻射計算過程中涉及到的一個重要參數[37]。最近，Zhou等[38]基于理論分析，建立了一個新的無量綱數群（包含化學當量條件下燃料質量分數、燃料與空氣密度比和火焰Froude數），用于計算火焰輻射分數。與前人的模型相比較，該模型適用范圍更廣、可用性更強，孔口出口直徑達數百毫米，覆蓋氫氣、甲烷和丙烷等多種燃料垂直和水平噴射火，并涵蓋從亞音速到超音速范圍內浮力和動量控制的火焰射流，模型表達式如下：

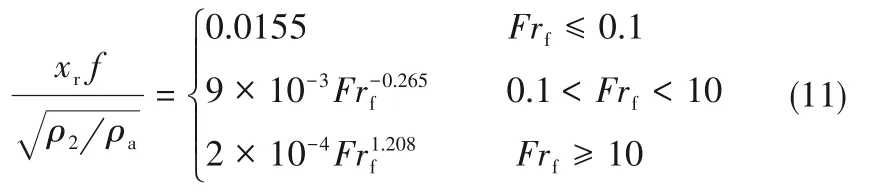
式中

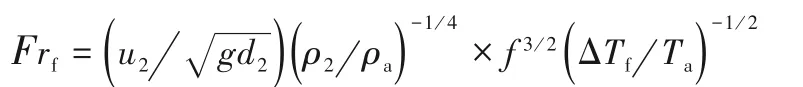
從實際應用角度出發，本文選用經典的點源模型，以建立一套簡單、實用的氫噴射火熱輻射危害快速評估方法，并為其后期開發與推廣應用奠定基礎。點源模型反映了被輻射目標受到的輻射通量與目標點到火源中心距離平方之間一種簡單的反比例關系，即[25]：

4 模型方法說明與應用

4.1 模型方法說明

高壓氫氣儲運系統泄漏引發噴射火輻射熱通量計算流程如圖3所示。

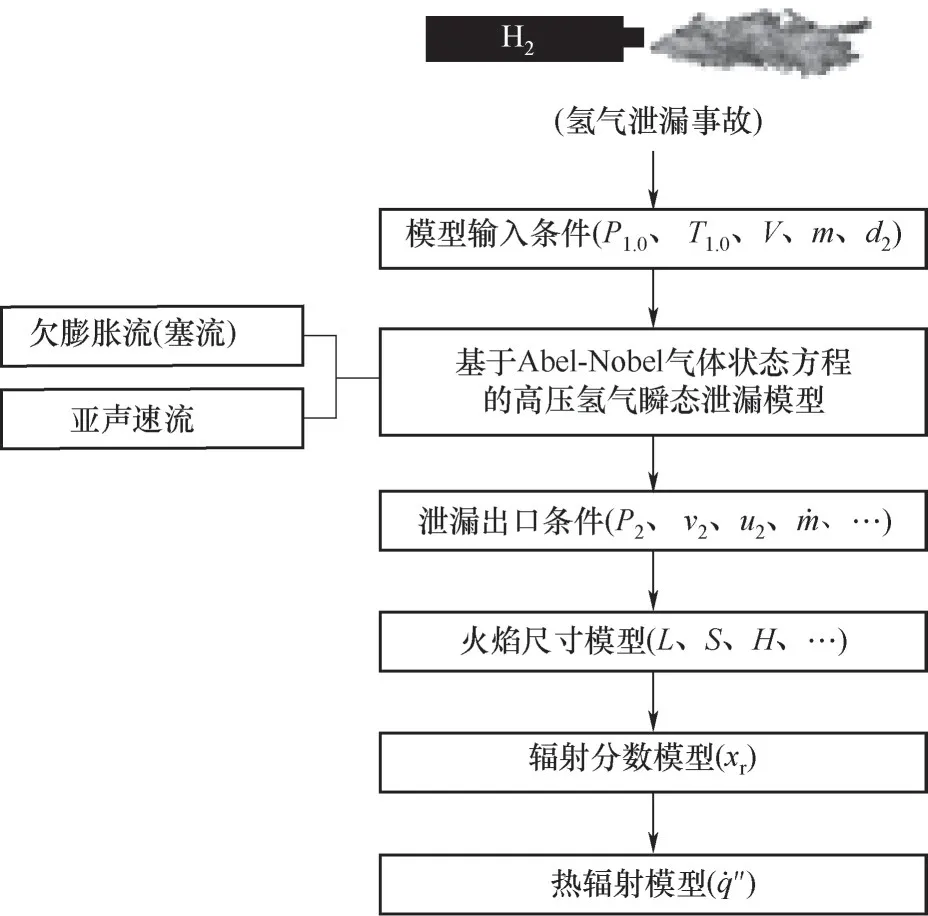
圖3 高壓氫氣泄漏引發噴射火輻射熱通量計算過程Fig.3 Calculation process for radiant heat flux from jet fire induced by high-pressure hydrogen leakage

基本步驟分為以下5個部分：

（1）收集和分析泄漏系統相關信息，包括氣源初始溫度（T1,0）和壓力（P1,0）、泄漏氣體體積（V）或質量（m）及泄漏出口直徑（d2）等；

（2）基于Abel-Nobel泄漏模型計算泄漏出口氣體狀態參數（P2、v2、u2和m?等）；

（3）計算火焰幾何尺寸（L、S和H）；

（4）計算火焰輻射分數（xr）；

（5）計算在某一距離處目標接受的輻射熱通量（?）。

4.2 實驗數據來源

以下將應用本文所建立的高壓氫氣泄漏噴射火過程預測模型分別對Proust等[14]和Acton等[39]的實驗結果進行模擬驗證。如圖4(a)所示，Proust等的實驗裝置為Ⅳ型儲氣瓶（25 L），實驗在橫截面積為12 m2、長為70 m開放長廊中進行，瓶內壓力從90 MPa降至0.1 MPa，泄漏孔直徑為1~3 mm，采用丙烷燃燒器作為連續點火裝置形成水平氫噴射火，最大火焰長度接近7 m；Acton等的實驗布置如圖4(b)所示，該實驗在戶外大尺度測量條件下進行，通過管道將1個體積為163 m3氫氣儲存裝置（標稱壓力6 MPa）連接成閉合氣體循環回路，管道測試部分設置在連接管道下游的三通管路上，采用遠程控制啟動爆炸切割裝置誘導管道發生全管徑泄漏（泄漏尺寸取管徑的100%，即15.2 cm）引發垂直氫噴射火，最大火焰高度接近100 m，環境風速為1~2 m/s。表1給出了模擬計算上述不同實驗案例需要的模型輸入參數。

圖4 高壓氫氣泄漏實驗裝置Fig.4 Diagram of experimental setup for high-pressure hydrogen leakage

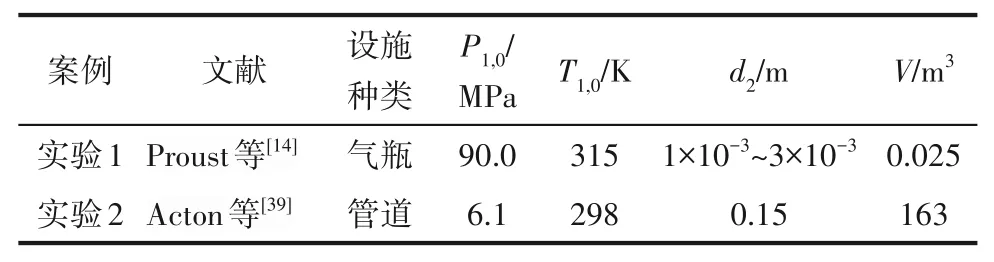
表1 模型輸入參數Table 1 Model input parameters

5 計算結果與分析

5.1 質量流量

實驗1（氣瓶）和實驗2（管道）中泄漏出口處氣體質量流量隨瓶內壓力/泄漏時間變化的計算值和測量值比較如圖5所示。實際氣體流動會產生能量損失，這與氣體沿程阻力損失以及流經管件閥門、管截面突然擴大或縮小等區域產生的局部損失有關。為此，本文對氣體欠膨脹射流模型進行改進，在模型中引入流出系數Cd，它實際上反映了出流時的阻力損失及過流斷面的減少對出流流量的綜合影響[40]。文獻[41]中給出了流出系數一般計算公式（式中，β為噴口直徑與管道直徑的比值），可以發現流出系數與噴口直徑呈負相關，且與Reynolds數Re呈正相關。而對于典型結構的流量噴嘴，當Re>106，Cd一般為0.99或更高。另外，在實驗1中，Proust等[14]基于Cd=1假設計算出不同泄漏孔直徑條件下泄漏孔氣體質量流量的變化，通過與實驗測量值進行對比，發現1 mm泄漏孔直徑情況下的氣體質量流量計算值與實驗測量值基本吻合，但隨著泄漏孔直徑的增加（即d2=2 mm和3 mm），計算結果會出現明顯偏差；隨后Cirrone等[30]利用CFD技術基于Cd=0.7假設對該實驗（d2=2 mm）進行了模擬，模擬結果與實驗測量值有很好的一致性。因此，本文對實驗1中d2=1 mm情況下流出系數取值為1，但對d2=2 mm和3 mm情況下的流出系數修正為0.7，修正后的計算結果與實驗測量值基本一致[圖5(a)]，注意到在d2=3 mm情況下，瓶內壓力較高時，Abel-Nobel氣體狀態方程計算值偏高，這可能與稱重裝置（精度±10 g）稱量誤差或模型固有缺陷（僅考慮分子體積的修正）有關。實驗1中1~3 mm泄漏孔直徑條件下，模型預測結果的相對 誤 差 分 別 為19.1%±11.5%、13.2%±16.8%和18.2%±23.1%。在高壓氫氣管道泄漏實驗中（即實驗2），由于氫氣從管道兩端釋放，且管道兩端均勻減壓，經由破裂管道兩端泄漏的氣體質量流量相等[42]，因此可以將總泄漏面積（2A）×流出系數（Cd）等效折算為一端泄漏情況（如圖2所示）。假設等效泄漏面積為A′，據此可采用一種“等效”直徑泄漏的方法來計算破裂管道兩端氣體泄漏總量，具體計算方法如下：

由圖5(b)可知，若管道內氣體流動無能量損失（即Cd=1），基于Abel-Nobel氣體狀態方程計算得到的泄漏出口氣體質量流量明顯高于實驗測量值。考慮到管道內氣體流動存在較大能量損失，通過進一步修正流出系數，泄漏出口處氣體質量流量將隨流出系數減小而逐漸降低，直至接近實驗測量值。當Cd=0.3時，模擬計算結果與實驗測量值基本一致，相對誤差為21.0%±16.3%。顯然，不同高壓氫氣儲運系統發生泄漏時流出系數差別較大，需根據實際情況加以分析確定。

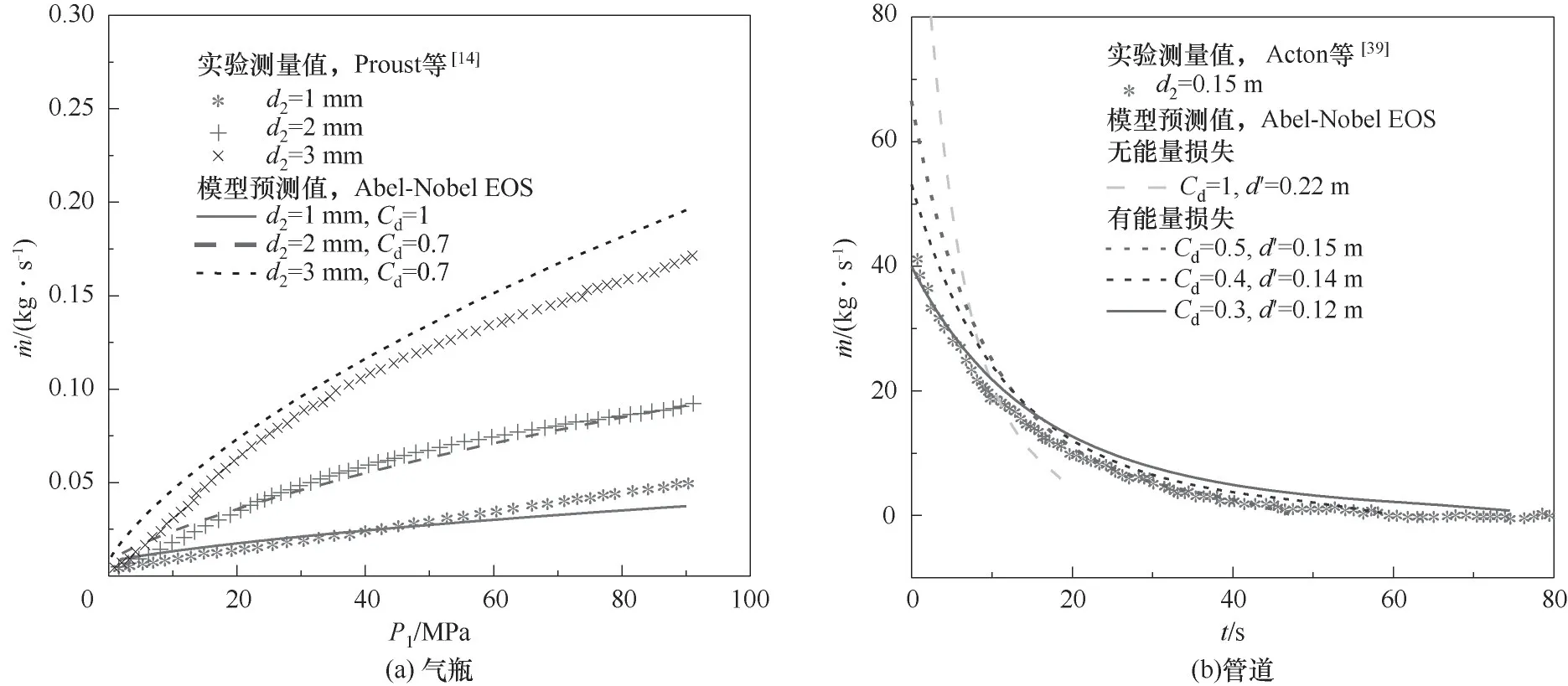
圖5 氣體質量流量隨瓶內壓力/泄漏時間變化的計算值和測量值比較Fig.5 Comparison of calculated and measured results for the variation of gas mass flow rate with gas pressure in reservoir or leakage time

5.2 火焰長度

實驗1（氣瓶）和實驗2（管道）中噴射火焰總長度隨瓶內壓力/泄漏時間變化的計算值和測量值比較如圖6所示。注意到Abel-Nobel氣體泄漏模型將高壓氣體泄漏過程近似認為是等熵流動，即氣體泄漏時間較短不足以與外界熱交換，但在實際工程中，氣體與外界有可能發生熱交換，使氣流基本上保持與周圍環境相同的溫度，Cirrone等[30]在CFD模擬中將高壓氫氣泄漏過程按“絕熱+等溫”流動處理獲得了較好的結果，也說明了引入等溫流動處理方法對改進模型預測精度的有效性。因此，本文同樣引入等溫流動處理方法，注意在等溫流動過程中（T2=T1），絕熱指數k=1，因此P(v-b)=RgT=C1，結合能量方程

則有

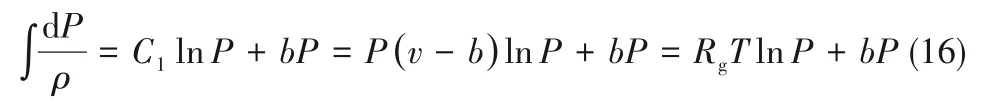
所以

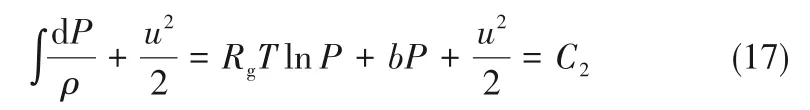
又因為進口流速u1與出口流速u2相比很小，可以忽略[43]，故

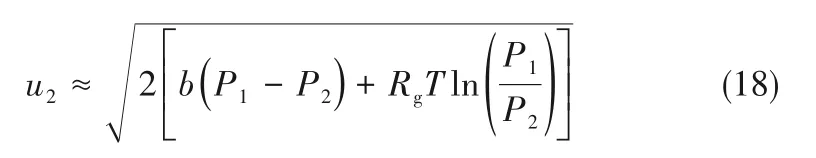
按照此方法計算出的火焰總長度與實驗測量值具有較好一致性。實驗1中1~3 mm泄漏孔直徑條件下，模型預測結果的相對誤差分別為8.9%±9.7%、4.7%±4.3%和8.2%±6.9%。注意在實驗2中，氫噴射火焰總長度在泄漏的初始階段快速升高，6 s后達到最大值，此時根據氣體瞬態泄漏方程計算得出管道內壓力降至4 MPa，故將此壓力作為新的初始壓力值來計算管道泄放階段火焰總長度的變化。實驗2中模型預測結果的相對誤差為27.3%±14.1%，由于該實驗為大尺度且在戶外進行，影響因素較多，所以產生的誤差較大。總的來說，結合等溫流動處理方法，Molkov等[7]提出的火焰長度預測模型可以較好地描述高壓氫氣泄漏引發的噴射火焰總長度變化情況。但此模型還需進一步完善，因一方面未考慮高壓氫氣管道泄漏點燃后短暫時間內發生的爆炸，通常表現為在持續噴射火之前，伴隨爆炸產生的巨大火球；另一方面還忽略了環境風速的影響。

5.3 火焰輻射

在實驗1中，5個輻射熱流計與水平噴射火焰軸線方向夾角均為45°，呈直線排列，距出口水平距離依次為1、1.5、2、3和4 m，如圖7(a)所示。在實驗2中，4個輻射熱流計被安置在地面三腳架上，離垂直噴射火焰中心水平距離依次為40、50、60和80 m，如圖7(b)所示。圖8進一步給出了實驗1（氣瓶）和實驗2（管道）中噴射火焰輻射熱通量隨泄漏時間/測量距離變化的計算值和測量值比較。從預測結果可以看出，在實驗1中距出口水平距離依次為1、1.5、2、3和4 m處預測結果的相對誤差分別為25.7%±18.8%、21.5%±15.0%、15.0%±10.1%、10.7%±9.4%和15.0%±10.6%，除水平距離為1 m和1.5 m處的計算值偏高，其余位置處的預測結果相對誤差較小，接近射流出口處的預測偏差可能是由于高壓氫氣突然釋放時夾帶灰塵顆粒等對火焰輻射產生干擾所造成。另外在氣瓶泄放初始階段（10 s左右）的火焰輻射熱通量計算值與實驗測量值也存在差異，這可能與預測模型未考慮此階段實際上形成的（強輻射性）球形火焰有關[44]。而在實驗2中，模型預測值與實驗測量值整體吻合較好，火源熱釋放速率為1500 MW和2800 MW時，預測結果的相對誤差分別為16.1%±17.0%和8.2%±1.7%。總的來說，運用簡單的點源模型對兩起高壓氫氣泄漏實驗案例中噴射火焰輻射熱場變化進行預測，其預測曲線與實測曲線變化趨勢基本一致，且遠場輻射熱通量預測值與實驗測量值一致性更好，同時也說明本文所提出高壓氫氣泄漏噴射火過程預測模型預測結果準確，與實際工程相符，在實用性及有效性等方面滿足工程需要。但需要注意的是，目前關于高壓氫氣泄漏誘發噴射火相關實驗數據還比較少，為進一步驗證模型的魯棒性帶來一定困難，后期還需要更多的實驗數據和案例作為支持。

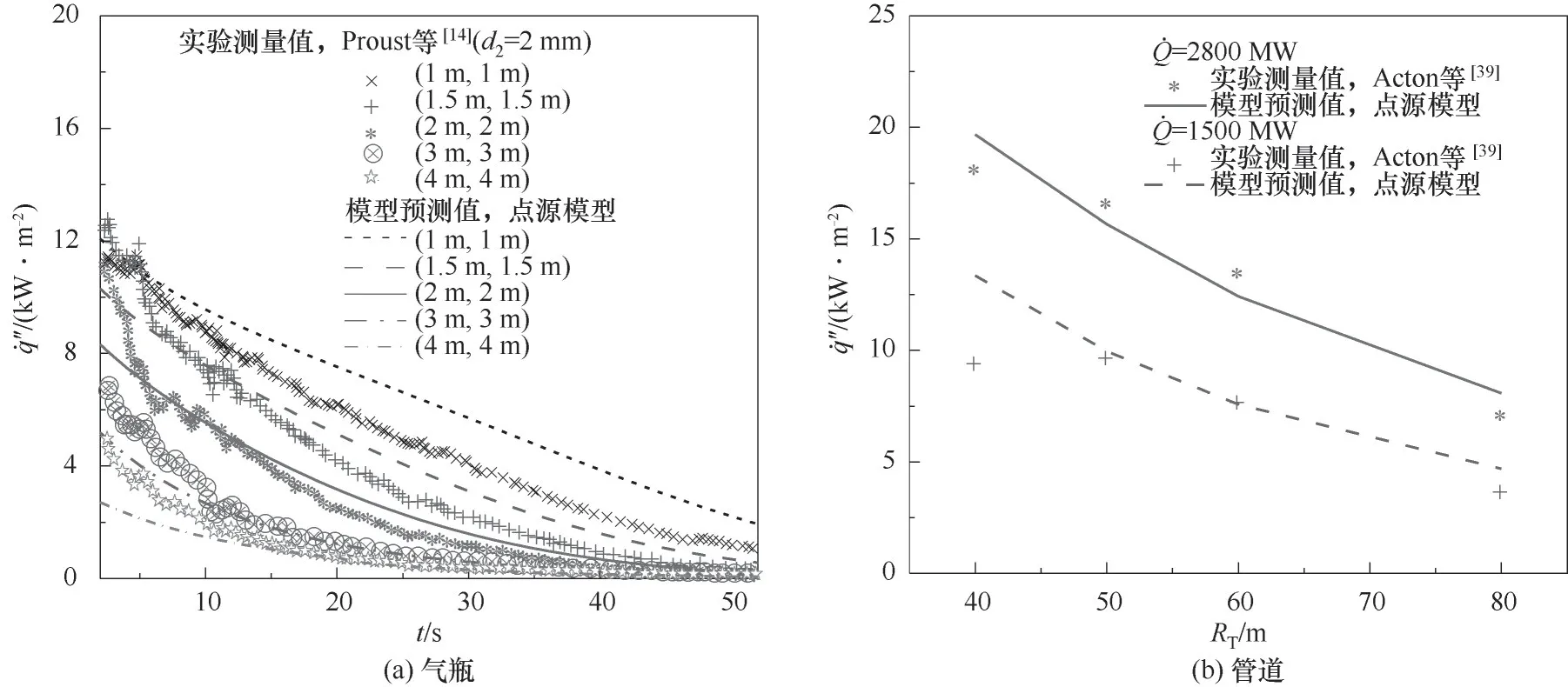
圖8 火焰輻射熱通量隨泄漏時間/測量距離變化的計算值和測量值比較Fig.8 Comparison of calculated and measured results for the variation of radiant heat flux with leakage time or measured distance

6 結 論

本文對高壓氫氣儲運設施泄漏形成噴射火進行了研究，通過理論分析和實例驗證的方法，詳細探討了高壓氫氣泄漏過程及其引發噴射火幾何尺寸和輻射熱場的變化。主要結論如下。

（1）基于Abel-Nobel氣體狀態方程、火焰尺寸模型、輻射分數模型和熱輻射模型構建的高壓氫氣泄漏噴射火過程預測模型，可以較準確地描述泄漏出口氣體質量流量、氫噴射火長度和輻射熱場等的變化。

（2）分別通過兩起高壓氫氣泄漏實驗案例（高壓氫氣瓶和管道），根據在實驗現場獲取的模型輸入參數進行快速模擬計算，計算結果與實驗測量數據結果基本一致，驗證了所提模型的有效性以及簡化假設的合理性。

（3）本文工作為氫能安全利用以及事故防控提供重要的指導作用，并為CFD仿真在高壓氫氣泄漏引發噴射火災害計算中提供簡化模型方案，在今后研究中還可以考慮管道爆炸、環境風速和其他熱輻射模型，以進一步提升模型預測精度和適用性。

符號說明

A——泄漏面積，m2

A′——等效泄漏面積，m2

b——氣體比體積修正項，m3/kg

C,C1,C2——常數

Cd——流出系數

c——當地聲速，m/s

d——泄漏直徑，m

d′——等效泄漏直徑，m

Fr——Froude數

Frf——火焰Froude數

f——當量比下燃料質量分數

g——重力加速度，m/s2

H——火焰總長度，m

ΔH——燃料燃燒熱，kJ/kg

k——絕熱指數

L——火焰長度，m

Ma——Mach數

m——氣體質量，kg

m?——氣體質量流量，kg/s

P——氣體絕對壓力，Pa

Q?——熱釋放速率，kW

q?″——輻射熱通量，kW/m2

Rg——氣體常數，J/（kg·K）

RT——目標點到火焰中心的距離，m

Re——Reynolds數

S——推舉高度，m

T——氣體熱力學溫度，K

ΔTf——絕熱火焰溫升，K

t——時間，s

Δt——時間步長，s

u——氣體流速，m/s

uw——風速，m/s

V——氣體體積，m3

v——氣體比體積，m3/kg

X——無量綱變量

xr——輻射分數

β——噴口直徑與管道直徑比值

θ——目標的法線與目標和火焰中心連線之間的夾角,(°)

ρ——氣體密度，kg/m3

τ——大氣透射率

υcr——臨界壓力比

下角標

a——環境

f——火焰

T——目標

(t)——時間迭代步數

0——初始時刻

1——系統內

2——泄漏出口處