一種基于艾森斯坦整數的SCMA碼本的優化

曾慧，李旭東

（西華大學理學院，成都 610039）

0 引言

隨著信息時代的快速發展，通信設備出現了爆炸式的增長[1]，這些智能設備（智能手機、筆記本電腦、運動手環等）相互連接，提供無處不在的無線通信服務，使得人們的生活方式變得越來越便捷。在移動通信技術和物聯網應用不斷發展的大背景下，第五代通信系統（5G）為無線技術的發展提供了更加廣闊的領域。碼分多址作為一種非正交多址（NOMA）技術，能有效地利用消息傳遞算法（MPA）的稀疏性來進行多用戶檢測，讓每一個用戶在碼分多址系統中通過一個唯一的數據信號，從而使該碼分多址系統的大多數序列條目歸零[2]。由于近年來，頻譜效率、大規模連接和超低訪問延遲等問題受到了越來越多的研究關注，為滿足各種嚴格的服務質量要求，低密度簽名的碼分多址（LDS-CDMA）的概念很快被擴展到稀疏碼分多址（SCMA）中，每個用戶根據瞬間輸入的消息從碼本中去發送一個稀疏碼字。稀疏碼分多址（SCMA）作為一種有競爭力的碼域方案，將調制和稀疏擴頻結合來增加接入的用戶數量，從而有效地提高系統的頻譜效率[3]。由于在大多數研究中，SCMA信號是通過將輸入比特映射到適當設計的多個多維碼字來享受所謂的“星座成形增益”，所以SCMA的誤碼率性能接近于最大似然接收機[4]，其中碼本的設計對于提高碼分多址系統的誤碼率性能是至關重要的。

至今為止，在已有的文獻中，已經提出了許多碼本結構，但它的最佳設計在很大程度上仍然是具有挑戰性的。在現有工作中，關于SCMA碼本設計的大多數是從增大組合星座點間的最小乘積距離（或最小歐幾里德距離）的單個多維母星座入手，利用該母星座，通過相位旋轉、交織和置換等一系列操作生成多個稀疏碼本[5]。但這也導致星座的功率不平衡，而功率不平衡的星座是有助于放大“遠近效應”，能從每個資源節點相關的稀疏碼本中看到用戶功率的變化，這對于在微波功率放大器中增強干擾抵消是有用的。因此也有文獻利用在下行鏈路傳輸的不同用戶之間具有的功率變化來開發一種新的SCMA碼本解決功率不平衡的問題[6]，通過分析優化每個碼本的最大功率密度，然后采用遺傳算法優化合成疊加星座[7]的最大功率密度，其中所提到的遺傳算法[8]是一種在工程中得到廣泛應用的隨機優化方法。盡管如此，最優SCMA碼本的設計仍然是一個開放性的問題。

本文借助艾森斯坦數提出了一類新SCMA碼本設計方法，利用了艾森斯坦整數在復平面內構成艾森斯坦環[9]的特點，通過計算這些點到復平面中心的距離，以保證每個用戶傳輸碼字均有較大的最小歐式距離，并將總星座圖拆分成三個子星座圖，以此增大不同資源塊上相同用戶的相同碼字之間的距離，讓每個用戶的每個碼字功率差別變小，通過仿真結果表明，在瑞利衰落信道[10]下，我們提出的碼本系統可以達到與華為SCMA碼本相當的誤碼率性能，在高斯信道下可以達到更好的性能。

1 SCMA系統模型概述

可以考慮一個上行SCMA系統模型[11]，如圖1所示，在這種情況下，正交時頻資源塊數量k=4；用戶數量J=6；每個用戶使用的星座點個數M=4。在發送端，SCMA系統將輸入的比特流序列直接映射成多維復數域碼字，各個用戶的碼字以稀疏擴頰的方式，在正交時頻資源快上疊加。在接收端，根據碼字稀疏的特性，進行算法檢測，從而達到恢復原始比特流的目的。

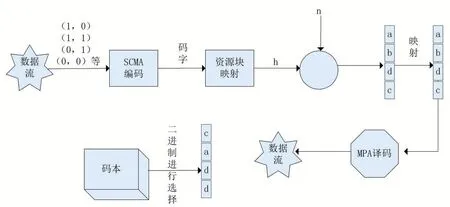
圖1 上行SCMA系統模型

在SCMA系統中，用戶數目和資源塊之間的關系可以用因子圖矩陣F來表示，當且僅當矩陣中的元素不為零時，用戶在資源塊上傳輸數據，當用戶在發送信號時，接收到的信號可用Y表示為：

其中y j表示用戶j發送的碼字，h j表示基站與用戶j的信道狀態，Z n表示資源塊上n的信道噪聲。所以在資源1處接收到的信號可以表示為：

公式中ε1表示占用資源塊1的用戶的一個集合，因為SCMA碼本存在稀疏性，所以用戶只在某些資源塊上進行傳輸。

2 SCMA碼本設計步驟

對于SCMA碼本來說，SCMA系統的好壞與碼本的設計是存在聯系的，而對于SCMA編碼來說，是把每個用戶的比特數據變成多維向量，來取代傳統CDMA中的調制和擴頻，從而使得系統整體容量得到大幅度提升。SCMA碼本設計過程可以利用星座函數[12]，首先生成M個N維用戶星座C j，再利用映射矩陣V j將C j映射成SCMA的碼本X j，該過程可用公式表示：

在公式（3）中，b j用來表示用戶j輸入的比特序列。

SCMA碼本用K維向量X j表示，產生過程可以表示為

設K維向量,K維向量G=，則給定結構為σ(V,G:J,M,N,K)的SCMA碼本，此設計問題便可以表示為：

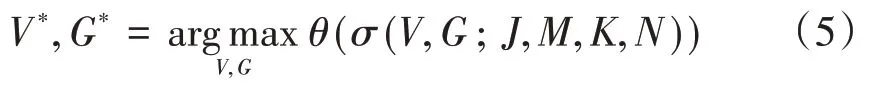
其中θ為一個給定的設計性能評價準則，而這個設計準則存在一個問題，就是在確定時存在難度，不容易去得到這個θ，所以在SCMA碼本設計中，設計的關鍵就在于怎么去設計它的映射矩陣以及總星座等問題，具體可以分為以下4個部分。

（1）映射矩陣設計。在SCMA里，可以通過映射矩陣W j而得到映射矩陣F，不同的在于這里的W j表示的是第j個用戶。因子矩陣F=(f1,f2,…,f J)是K×J的一個稀疏矩陣，f j和映射矩陣W j存在如下關系[13]：

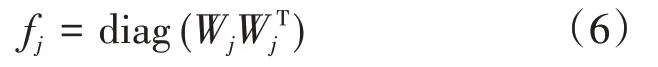
由于在同一資源塊節點上，映射矩陣的集合W決定了相互影響的用戶層數，不僅如此，映射矩陣的集合W也能夠影響MPA在接收端的解碼，具體來說，會在解碼計算速度上產生影響，這個產生的原因也跟SCMA碼字的稀疏性是存在關聯的，另外呢，MPA解碼的計算量其實也與碼本的碼字有聯系。一般設計的準則是這樣表示的：

其中W j∈B K×N，并且W i≠W j,?i≠j，公式（7）中W[?]j比較特殊，表示沒有零行的一個映射矩陣。我們可以詳細分析去獲得一個可行的方案，利用上述所提到的一些條件進行相應的研究，結合起來獲得我們所需要的方案，一般來說，設計出來的映射矩陣要在用戶數量上進行考慮，也要對資源塊上的用戶進行計算，對于SCMA系統來說，過載率要滿足λ=J/K，兩外，矩陣中的元素也要滿足一定的關系。

（2）多維星座的設計。如果已知映射矩陣W的集合，則SCMA碼本設計的最優化問題可簡化為如下的求解形式

具體來說。上述的求解問題就變成考慮如何設計出J個N維映射星座的問題。N維映射星座的設計雖然比較復雜，但這是設計碼本的關鍵之處，具體來說，我們可以考慮從歐式距離和乘積距離入手，怎樣去設計一個比較大的是優化的重中之重，可以通過對星座算子的計算從而得到各個用戶的星座。碼本設計的過程則可以分為：首先設計母星座，其次將母星座進行變換，最后便可以得到各個用戶所需要的碼本。為了增大母星座最小歐式距離，降低峰均功率比，我們采用如下的母星座結構GL：

（3）設計星座矩陣。星座矩陣通常由兩部分結合而成，設計一個好的星座矩陣對于碼本來說，是非常重要的。通常星座矩陣可以用K×J形式來表示，因子矩陣F確定了各星座位置,所以星座矩陣D M k,j可表示為：

且S k,rand(i)≠S k,rand(j)(i,j∈{1,2,…,d r})，其中DM k,j表示用戶j在資源塊k上可能取值的集合；{S1,k,S2,k,…,S d r,k}就是一個集合，這個集合可以重新進行隨機排列，第p個值由S k,rand(p)來表示，其實，在公式（10）中，所表示星座矩陣和星座圖是存在一定對應關系的，具體而言，就是去觀察矩陣中的行與列，來找到其中的聯系。

（4）生成用戶碼本。為了得到每一個用戶的碼本，可以將DM k,j中的每一列都進行展開，這樣讓矩陣的維數產生變化，來取得我們所需的碼本，具體表示為：

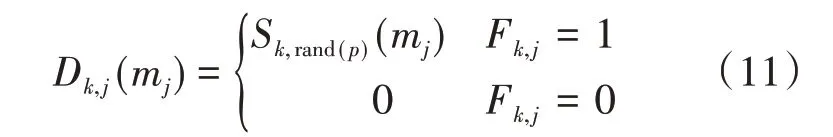
其中m j∈[1,M]，D k,j(m j)表示用戶j采用碼字m j時該碼字的第k個值。

3 艾森斯坦整數的碼本設計及優化

3.1 艾森斯坦整數

的復根。艾森斯坦整數可以定義為以下形式：

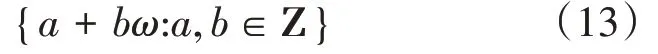
其中a和b表示整數，ω表示三次單位根。

在代數數域Q(ω)中，艾森斯坦整數具有可形成一個交換環的性質，然后，我們可以將艾森斯坦整數進行一定的運算，最后去得到艾森斯坦整數環，記為Z[ω]，艾森斯坦整數環是一個歐幾里德域，根據艾森斯坦整數的定義，在區域D={(x,y)|-4≤x≤4,-4≤y≤4}上，可通過Matlab繪制出艾森斯坦整數在復平面上對應的點，如圖2所示。

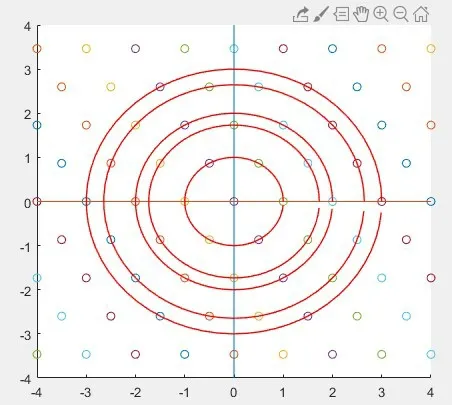
圖2 艾森斯坦整數的前5個圓

觀察上面的圖，我們通過計算可以發現一個特別之處，有6個點一個半徑為r1的圓上，這6個艾森斯坦整數點還構成了一個正六邊形，所對應復數也可以計算出，類似地還可以得到半徑為r2,r3,r4,r5的圓上的艾森斯坦整數，其中r5=3的圓上的6個艾森斯坦整數點也構成了正六邊形，可計算出其艾森斯坦整數對應的復數。

3.2 碼本構造以及優化

假設有6個用戶在4個資源塊上傳輸數據，每個用戶均在傳輸，定義一個εk,1≤k≤K，來表示具體的傳輸信號狀況，選擇如下的因子矩陣作為本構造的因子矩陣:

由 式 可 知ε1={2,3,5},ε2={1,3,6},ε3={2,4,6},ε4={1,4,5}，對于K=4，J=6的經典SCMA碼本結構來說，母星座可以簡化為如下結構，

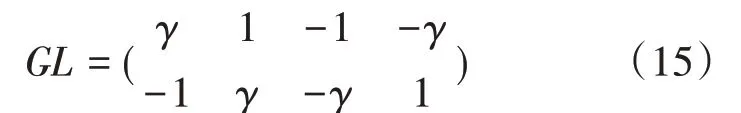
總星座可在艾森斯坦整數構成的復平面上選擇的兩個圓，并且圓上點的個數為6，通過分析，選擇半徑為r'1=r1=1,r'2=r5=3的兩個圓，此時母星座可進一步簡化為：

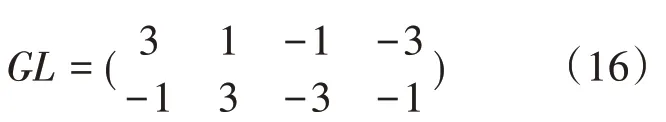
當選擇兩個圓之后，在這兩個嵌套著的艾森斯坦整數圓上分布12個星座點，這些點構成資源塊上的總星座圖，為保證每個用戶傳輸碼字均有較大的最小歐式距離，將總星座圖拆分成三個子星座圖，分別表示為S1,S2,S3，每個子星座圖S i的大小為4，這樣便可滿足每個用戶每次發送2比特的信息，拆分的結果如圖3所示：

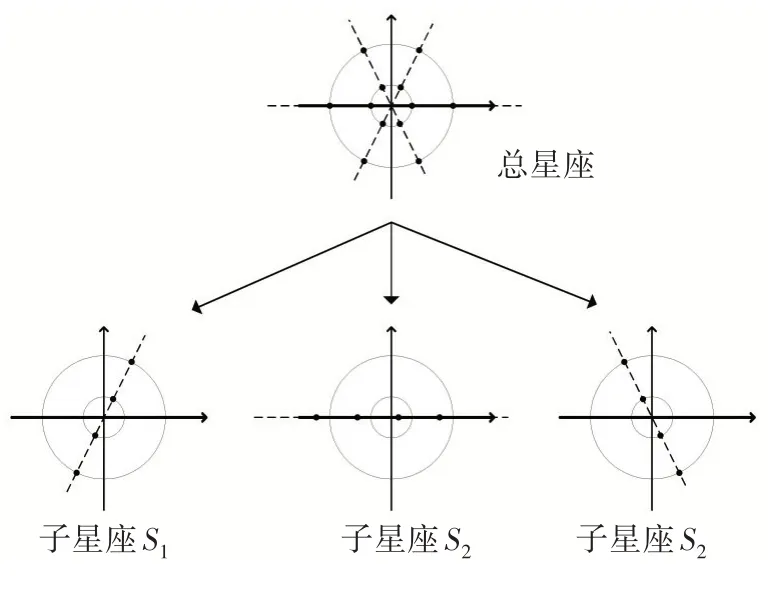
圖3 總星座拆分成子星座

在接收端，基于消息傳遞算法的用戶檢測性能[14]，主要取決于如下3個指標：相同資源塊上相同用戶不同碼字之間的距離；相同資源塊上不同用戶的相同碼字之間的距離；不同資源塊上相同用戶的相同碼字之間的距離。結合以上3點，適當改變碼字之間的距離，我們設計3個子星座圖的碼字分別為：

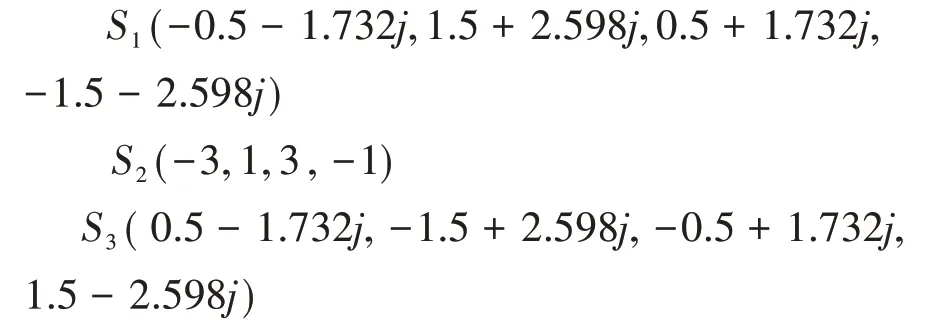
根據因子矩陣F，每個資源塊上實際傳輸3個用戶，并且每個用戶在不同資源塊上傳輸數據，因此，用戶和子星座之間存在多種多應關系，其中的一種關系如表1所示，表中S i表示用戶在資源塊上傳輸數據所使用的星座圖。

表1 用戶在資源塊上所用的子星座

在總的SCMA碼本中，為了增大不同資源塊上相同用戶的相同碼字之間的距離，同時保證每個用戶的每個碼字功率差別較小，對于表中的用戶3和用戶4,可以通過將子星座圖S3調整為子星座圖S3*，S1調整為S1*，即將碼字向左循環移動一位生成新的碼字：

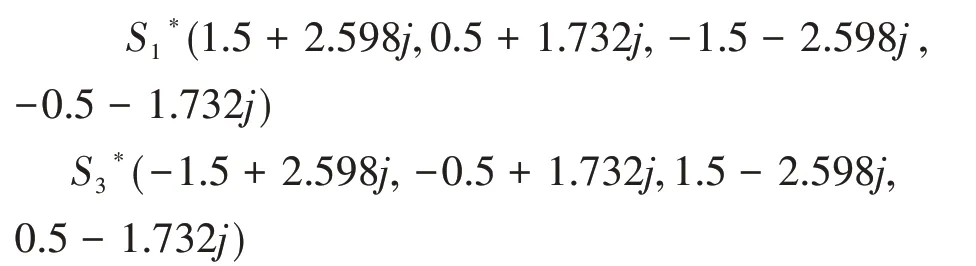
上述每個碼字的功率可用每個元素模長的平方來表示，為了同時與華為碼本和已有的艾森斯坦碼本進行性能比較，將每個用戶的碼本相對于華為的碼本的功率進行功率歸一化，得到新的系統碼本。功率歸一化的計算方法[15]表示為

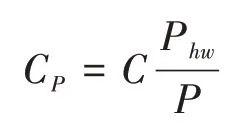
其中P hw代表華為公司提出的碼本矩陣中每個碼字的功率，P代表功率歸一化前用戶碼本中每個碼字的功率，C P代表功率歸一化后各用戶碼本矩陣中的元素，C代表功率歸一化之前各用戶碼本矩陣中的元素，功率歸一化后，用戶碼本中每個碼字的功率都與華為碼本中每個碼字的功率相同。歸一化之后新的碼本如表2所示。

表2

在AWGN信道下，把采用上述方法設計出來的碼本同艾森斯坦整數碼本和華為所提出的碼本進行仿真，在MPA算法下得到的誤碼率性能曲線如圖4所示，從圖中可以看出，相比于已有的艾森斯坦整數碼本，新提出的碼本在高信噪比時誤碼性能具有更大的增益，數據表明和華為碼本相比，當誤碼比特率為10-4時，它增加約0.8 dB的性能增益，相比艾森斯坦整數碼本碼本增加約0.1 dB的性能增益，因此，本文提出的優化的SCMA碼本在高信噪比下具有較好的性能。

圖4 不同碼本下的誤碼率比較

4 結語

在本文中，我們提出了一種新的SCMA碼本，它是建立在艾森斯坦整數的基礎上，對已有的碼本進行優化，通過增大了不同資源塊上相同用戶的相同碼字之間的距離，使得每個用戶的每個碼字功率差別變小，將歸一化方式以及各碼字功率進行調整，使得各用戶之間，以及不同碼字之間均保持有相同的功率，仿真結果表明，在AWGN信道中，我們所提出碼本相比于華為碼本和已有的艾森斯坦碼本具有更大的增益。