基于汽車價值鏈業務協同資源的配件銷量預測模型

孫磊，任春華，高雪芹，王波

（1.西南交通大學，制造業產業鏈協同與信息化支撐技術四川省重點實驗室，成都 611756；2.北京機械工業自動化研究所有限公司，北京 100120；3.成都國龍信息工程有限責任公司，成都 610036）

0 引言

隨著中國汽車工業的迅速發展，汽車銷售市場需求日趨飽和，市場競爭更加激烈。盡管在2020年新冠疫情的影響下，人們的消費需求有所降低，全球汽車產業鏈受到了巨大沖擊，但我國克服重重困難，其中汽車行業率先恢復生產。據公開資料顯示，2020年中國汽車銷量為2531.1萬輛，同比僅下降1.9%，降幅比上年大幅收窄了6.3%［1］。為了提高市場占有率，配件代理商必須向客戶提供優質的服務。這就要求代理商要有足夠的庫存以滿足及時發貨的需求，然而為了減少庫存成本，代理商又必須適當降低庫存。為了緩和這兩者之間的矛盾，通過汽車配件市場銷量預測，建立合理庫存管控機制顯得尤為重要。本文依托汽車價值鏈業務協同平臺［2］，面向產業鏈上的配件代理商，整理配件銷售業務數據，分析該企業在一段時間內的銷售情況，提出了一種BPGRU組合模型進行配件銷量預測，為配件代理商下一階段的配件進貨與庫存管控提供決策支持。

1 相關工作

隨著人工智能、機器學習等領域的高速發展，BP、GRU、ARIMA、LSTM等網絡模型廣泛應用于預測場景中，取得了一些豐碩的成果。馮晨等［3］提出了一種ARIMA、XGBoost和LSTM進行加權組合的預測模型，以提高多變量商品銷售的預測精度。鄧青等［4］在研究微博轉發行為時，采用BP神經網絡對突發事件的轉發量進行預測，獲得了極具參考意義的實驗結果。為更好地預測產品銷量短期及長期的變化趨勢，葛娜等［5］將Prophet與LSTM進行結合提出了一種新型組合預測模型。李祚敏等［6］引入鯨魚優化算法，提出了一個優化網絡權重的GRU神經網絡用于預測防曬用品的銷售情況。Wang等［7］收集了從2008年起至2017年臺灣出口經濟的關鍵指標數據，并通過相關分析選擇重要的變量，采用人工神經網絡對注塑機的銷售情況進行預測。

針對汽車零配件銷售及需求情況的預測，在近年來也成為一項熱點研究。荊園園等［8］通過研究影響汽車零配件需求量的各種因素，提出了一種基于BP神經網絡的預測模型。呂鵬飛等［9］構建了一個基于回聲狀態網絡的配件庫存預測模型，并將其應用于汽車配件的需求預測問題。Gong等［10］將季節變化指數引入到GM（1,1）中，以提高模型在預測非線性汽車零部件銷售情況時的準確性。方瑜等［11］對二手汽車售后配件銷售規律進行了分析，并提出了一個可有效解決二手汽車配件預測問題的ARIMA模型。此外，方瑜等［12］還提出了一種結合ARIMA與BP神經網絡的組合模型對二手汽車配件需求進行預測，進一步通過真實數據集證實了該模型的有效性。

2 組合預測相關模型構建

2.1 模型相關理論

本節主要介紹BP神經網絡和GRU網絡模型，分別從其內部結構和核心原理進行闡述，方便進行兩個模型的有效組合。

2.1.1 BP神經網絡

BP神經網絡是由Rumelhart等［13］提出的，它是一種誤差逆傳播的多層前饋網絡。通過反向傳播的方式來調優網絡的權值和閾值，使得其誤差平方和最小。BP神經網絡的拓撲結構包括輸入層（Input Layer）、隱藏層（Hide Layer）和輸出層（Output Layer）。其網絡拓撲結構如圖1所示。

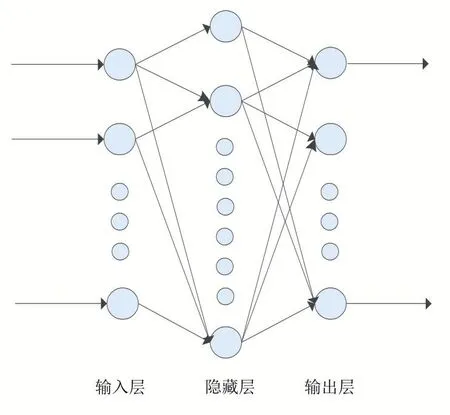
圖1 BP神經網絡拓撲結構

BP算法的核心為信息的正向傳播與誤差的反向傳播［14］。

（1）信息的正向傳播。在信息的正向傳播過程中，數據經由輸入層進入，經過隱藏層的處理之后再次進入輸出層。當輸出層的輸出結果與期望的輸出結果不同時，便會進入誤差的反向傳播過程［15］。

BP神經網絡的輸入層與隱藏層節點之間以權重連接。正向傳播時，隱藏層的第一個神經元從輸入層的每一個神經元處得到輸出值，加權求和，閾值，激發函數f1，得到該神經元的輸出值如公式（1）所示：

輸出層第一個神經元a1得到隱藏層每一個神經元輸出值，加權求和，閾值，激發函數f2，得到該神經元的輸出值如公式（2）所示：

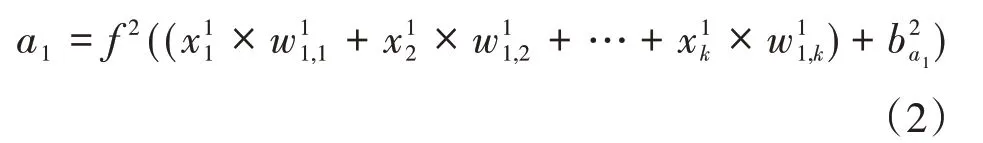
（2）誤差的反向傳播。向輸入層輸入n個I維數據樣本，正向經隱藏層處理后，傳入輸出層，得到實際輸出a。在輸出層把實際輸出a和期望輸出t進行比較，計算均方誤差如公式（3）所示：

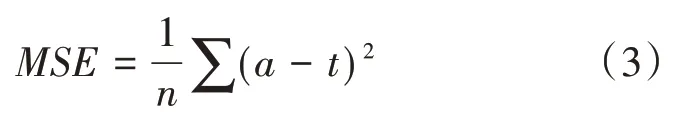
若M S E沒有達到預設的誤差精度ε，算法進入誤差的反向傳播過程。M SE以梯度形式按原來正向傳播的通路逐層反向傳回。同時，反向傳回的MSE被分攤給各層所有神經元以獲得各層神經元的誤差信號M SE j（j=1，2，3）。MSE j作為修正各連接權值和閾值的依據，對其進行修改。

BP算法反復運行信息的正向傳播和誤差的反向傳播兩個過程，直至誤差信號MSE收斂于預設的精度ε或達到預設的最大訓練次數［16］。

2.1.2 GRU網絡模型

LSTM模型廣泛應用于時間序列數據的預測，但由于其內部結構復雜，導致LSTM模型在進行數據訓練時需要花費很長時間，所以出現了許多LSTM變體。Cho［17］于2014年提出了GRU網絡模型。GRU通過將遺忘門和輸入門結合在一起形成了更新門（Update Gate），并且將細胞狀態和隱藏層狀態合并在一起，使得模型結構比LSMT模型更加簡單。GRU內部結構如圖2所示。

圖2 GRU內部結構

GRU的計算公式如式（4）—式（7）所示。

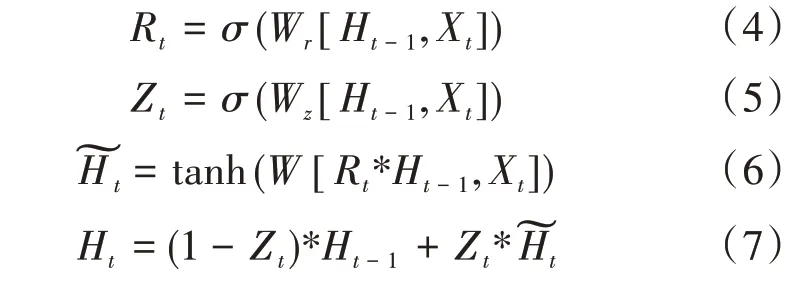
其中W r、W z和W表示需要訓練的權重矩陣。當R t越接近于0，則表明前一時刻貢獻的有效信息越少，而Z t越小，則表明前一時刻貢獻的有效信息越多。

2.2 組合模型構建

BP網絡是目前應用最多的一種神經網絡，它具備神經網絡的普遍優點，能夠有效處理回歸問題，但對長時序列數據的感知能力有所欠缺。而GRU能夠有效地處理長時預測問題，且結構相比LSTM更簡單。因此，本文將基于BP和GRU網絡構建一種BP-GRU組合預測模型，用于汽車零配件銷售預測。BP-GRU模型的結構如圖3所示。

由圖3可知，BP-GRU模型首先利用BP網絡對數據的特征進行初步提取，接著利用GRU捕獲時間長期依賴性，最后將BP和GRU的預測結果進行加權融合，得到最終的預測結果。

圖3 BP-GRU模型結構

3 實驗分析

3.1 實驗環境及數據

本文實驗環境如表1所示。

表1 實驗環境

為驗證BP-GRU預測模型的準確性與高效性，本實驗采用3種數據集，分別是PRSA_Data_Wanshouxigong_20130301-20170228數據集（以下簡稱PRSA_Data_A）、PRSA_Data_2020.1.1-2014.12.31數據集（以下簡稱為PRSA_Data_B），和汽車價值鏈業務協同平臺上的某代理商平臺的2018—2020年的某配件的銷售數據。其中配件銷售數據的特征維度選擇整車保有量、使用時長、配件故障率。3種數據集分別對模型進行訓練與測試。

為避免原始數據在模型預測過程中由于數據不規范、缺失值和臟數據等對結果產生影響，首先要對采集的數據進行預處理。

（1）數據填充。在數據采集或者是記錄過程中出現了樣本數據為空或者是缺失的情況，采用數據填充的辦法，采用缺失位置前后數據的平均值來填充。

（2）數據歸一化處理。由于數據上下界存在較大波動，因此將數據進行歸一化處理如公式（8）所示，減少數據本身對預測結果的影響。

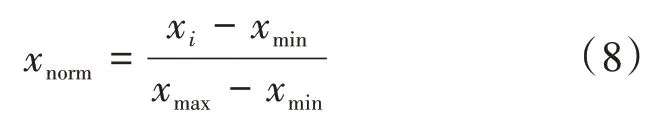
其中xnorm表示歸一化后的值，x i為歸一化前的值，xmin為最小的樣本值，xmax為最大的樣本值。

3.2 實驗方案及參數選擇

本文提出的組合預測模型采用M S E作為損失函數，使用Ad am作為優化參數。實驗中選用RMSE和M AE作為評測指標，以評估模型預測精度，兩個評價指標值越小，表明模型的性能越優。相關參數的取值情況如表2所示。評價指標計算如式（9）、式（10）所示。

表2 參數取值

其中n表示樣本數量，y i表示數據的值，表示預測值。

3.3 實驗結果分析

本文選取BP模型、GRU模型、CNN模型、LSTM模型和RNN模型作為對比實驗模型，與本文提出的BP-GRU模型進行性能對比，通過RMSE與MAE值進行比較。

PRSA_Data_A數據集的實驗結果如表3所示。BP-GRU模型的RMSE和MAE取值分別為24.87和12.35，均低于其他5個對比模型，說明本文提出的模型預測精度更高。

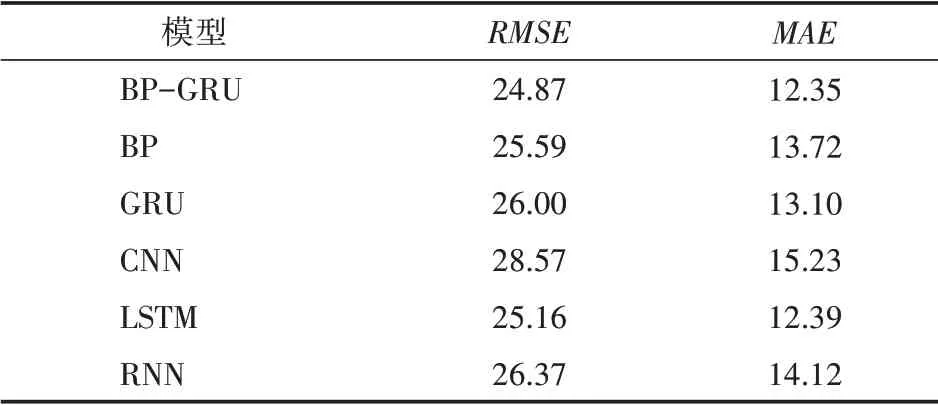
表3 PRSA_Data_A數據集實驗結果

PRSA_Data_B數據集的實驗結果如表4所示，在RMSE的比較中，LSTM的評價函數值是23.73排名第一，而我們的BP-GRU模型排名第二，但均比單獨的BP與GRU模型的效果更好。在M A E的比較中，BP-GRU取值是12.81，排名第一，而LSTM的M AE值是12.82。BP-GRU與LSTM模型性能相近，但BP-GRU優于BP、GRU、CNN和RNN。

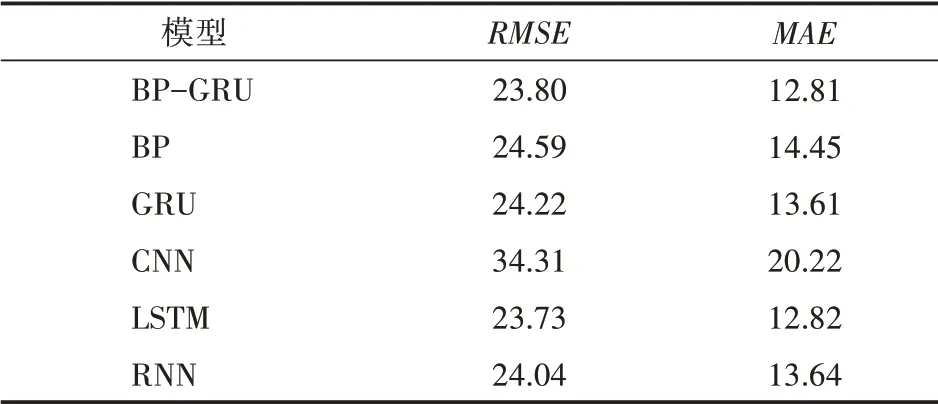
表4 PRSA_data_B數據集實驗結果

配件銷售數據集的實驗結果如表5所示，在R M S E的比較中，BP-GRU模型取值最低。在M A E上，LSTM的取值最低，BP-GRU模型排第二，但均比單獨的BP與GRU模型的效果更好。說明BP-GRU模型優于BP、GRU、CNN、和RNN。

表5 配件銷售數據的實驗結果

4 結語

本文以配件代理商的配件銷售數據為研究對象，提出了一種BP-GRU組合預測模型，用于預測配件的銷售情況，與此同時采用其他數據集與模型進行對比實驗。實驗結果表明，該組合模型在3種數據集上的預測效果比起其他單一的模型效果更好。該模型可應用于汽車價值鏈中售后服務時配件銷售預測情況，對代理商下一階段的采購提供決策支持。本文目前探索了BP-GRU模型的組合情況，下一步的工作可在此模型的基礎上進一步組合或是對該組合模型進行參數調優，以提高預測精度。