四足機器人Trot步態規劃與仿真分析

謝楚政，李 光，于權偉，吳陳成

1 研究背景

移動機器人可代替人類在一些復雜工況和惡劣環境中的工作，例如戰場的援救、地下管道的維修、高層樓房的建設等。不僅解放了人力、提高人們的生活質量、提升幸福感，更是對生產力技術的一次革命。移動機器人技術研究，目前已經成為國內外科研工作者的熱點研究領域[1]。

根據移動方式不同，可將機器人分為輪式機器人、履帶式機器人、步行機器人等。其中，步行機器人由于其結構模仿自然界中經過優勝劣汰、自然選擇后生存下來的各種生物結構[2]，所以相比輪式機器人、履帶式機器人具有更為優異的環境適應能力。設計性能優異的步行機器人，幾乎可以在各種路況的地面行走[3]。

四足機器人作為步行機器人中的一種，與雙足、六足機器人相比，具有更多優勢。雙足機器人運動穩定性較差，六足機器人運動速度較慢，而四足機器人兼具運動穩定性[4]、快速性[5]，以及較強的負載能力[6]等優勢。因此，本文選擇四足機器人作為研究目標。

目前，一些知名的研究機構已經研究出很多性能優異的四足機器人[4-6]。例如：波士頓動力學工程公司研究開發了Big dog[7]、Spot 和Spot Mini[8]，麻省理工學院研發了MIT Cheetah Mini[9]，瑞士蘇黎世聯邦理工大學機器人系統實驗室向外界展示了其開發的狗型機器人ANYmal[10]等。已有對四足機器人的研究工作，主要集中在結構設計、軌跡規劃、控制策略等方面[11]。而軌跡規劃是機器人運動研究中最關鍵的環節，因此機器人的使用離不開軌跡規劃[12]。不管是沒有環境感知能力的機器人按照既定的軌跡規劃進行作業，還是能夠獲取環境信息、進行自律控制的機器人作業，都需要提前做好軌跡規劃[13]。李貽斌等[14]提出了一種Trot 步態軌跡，并將其在液壓驅動四足機器人上實現。張培強等[15]采用調整腿長的方式，對四足機器人Trot 步態進行了優化。馬慧姝等[16]采用Kinect 攝像機采集犬類動物落足點，并用3 次樣條曲線擬合，對步態進行軌跡規劃。馬宗利等[17]采用調整質心位置的方法，提高了四足機器人坡面運動的穩定性。然而以上研究均未考慮四足機器人足端初始位置對Trot 步態穩定性的影響。

基于此，本研究針對四足機器人的軌跡規劃問題展開研究，在運動學分析的基礎上，從足端軌跡優化、初始足端位置選擇這兩個方面對四足機器人的Trot步態進行規劃，并用Matlab/Simulink 仿真平臺驗證此步態規劃的合理性。從而實現四足機器人以Trot步態相對穩定地行走。

2 四足機器人結構與運動學方程

2.1 四足機器人實體結構

四足機器人腿部結構一般分為4 種方式：“全肘式”、“全膝式”、“前膝后肘式”和“前肘后膝式”。為了滿足運動需求，一般四足機器人每條腿至少需要3 個自由度。

本文所研究的四足機器人采用的是“全肘式”結構，每條腿具有3 個旋轉自由度關節，結構示意圖如圖1 所示。

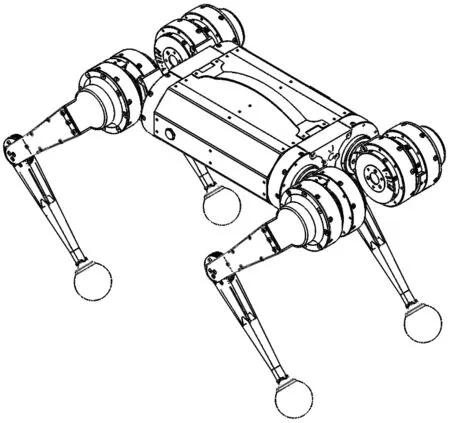
圖1 四足機器人結構示意圖Fig.1 Schematic diagram of quadruped robot structure

2.2 四足機器人正向運動學方程

采用改進D-H 法建立四足機器人的運動學模型，其示意圖如圖2 所示。

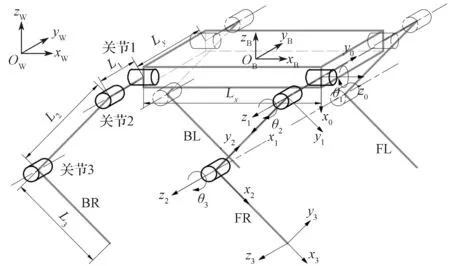
圖2 四足機器人的運動學模型示意圖Fig.2 Kinematic model of quadruped robots

在圖2 中坐標系皆為笛卡爾直角坐標系，3 個坐標軸下標為坐標系名稱。坐標系{W}為世界坐標系，其坐標原點為OW，3 個坐標軸分別為xW，yW，zW。坐標系{B}為機體坐標系，建立在機體質心處，其坐標原點為OB，3 個坐標軸分別為xB，yB，zB。坐標系{0}、{1}、{2}分別表示側擺、大腿、小腿坐標系。坐標系{3}為足端坐標系。θ1、θ2、θ3分別為3 個關節的轉動角度。Lx為機體前腿和后腿的關節1 沿xB軸距離，Ly為左右腿關節1 沿yB軸距離。四足機器人前左、前右、后左、后右4 條腿分別用FL、FR、BL、BR 表示。L1、L2、L3代表側擺、大腿、小腿連桿的長度，其中L1=76 mm，L2=210 mm，L3=210 mm。由于4 條腿坐標系的建立方法大致相同，圖中僅標出前右腿（FR）的坐標系，其D-H 參數見表1。

表1 四足機器人前右腿（FR）的D-H 參數Table 1 FR leg D-H parameters of quadruped robots

根據表1 所示的D-H 參數可求得足端正向運動學方程為

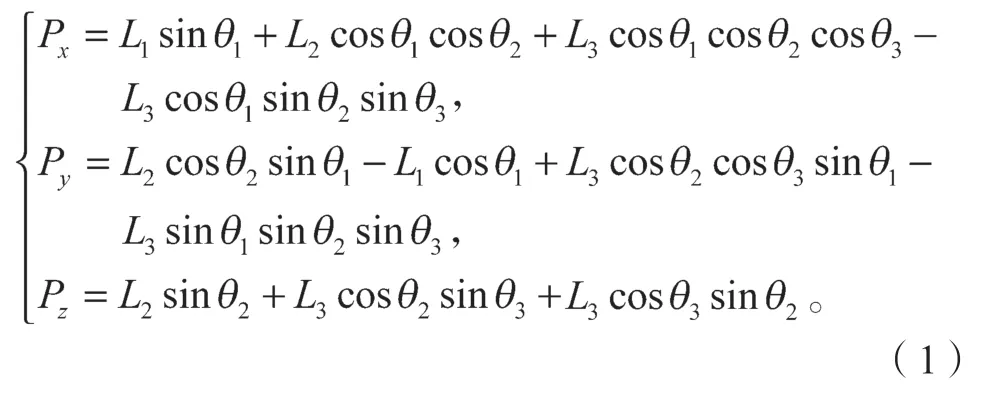
2.3 四足機器人逆向運動學方程

四足機器人逆向運動學的簡化參數示意圖如圖3所示。

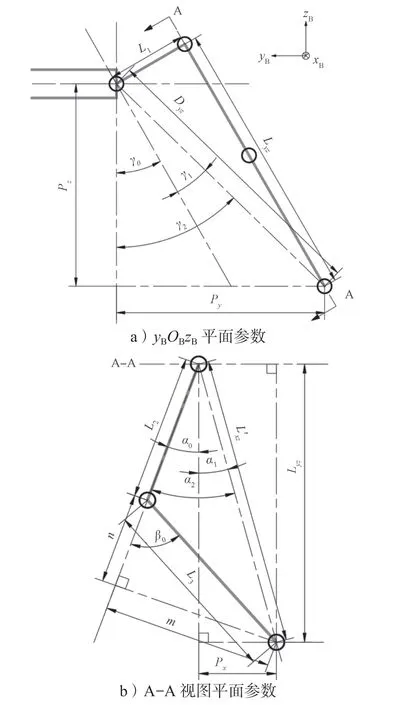
圖3 FR 腿的逆向運動學參數示意圖Fig.3 FR leg inverse kinematics parameters of quadruped robots

四足機器人的逆向運動學求解是軌跡規劃、運動控制以及其他相關研究的基礎。常用的方法有解析法、幾何法、迭代法等。本研究根據四足機器人的運動需求，采用幾何法求解逆向運動學方程。同正向運動學方程類似，四足機器人的4 條腿逆向運動學方程求解選取前右腿（FR）為例，以此說明逆向運動學方程的求解過程，所用到的參數已在圖3a、b 兩個平面標出。

由圖3a 可知，在yBOBzB平面內：

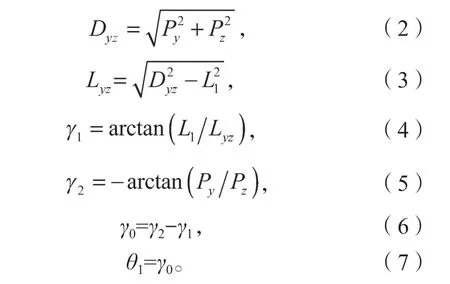
如圖3b 所示，在切于關節2、關節3 的A-A 視圖平面內：

由方程（2）～（15）可得到FR 腿逆向運動學方程為

3 四足機器人軌跡規劃

四足動物小跑過程中，同時抬起、放下前左、后右腿（或前右、后左腿）每條腿都會在支撐相和擺動相之間來回切換，以此形成對角Trot 步態，如圖4所示。

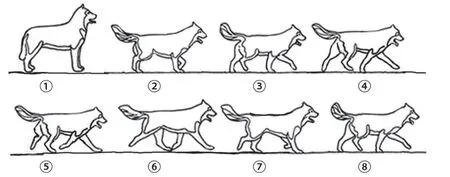
圖4 對角步態示意圖Fig.4 Diagram of diagonal Trot gaits

本研究中，四足機器人采取Trot 步態，同時抬起、放下相對的兩條腿，瞬時會有少于3 條腿支撐，沒有穩定的支撐域，屬于動步態的一種。

3.1 足端軌跡規劃原則及約束

為滿足實際使用需求，需減小四足機器人腿部在支撐相和擺動相之間切換時的足端慣性力以及與地面的沖擊力。因此本研究以足端沖擊力為0 的原則，即將足端狀態定為理想狀態，與地面接觸時，應該滿足足端速度與加速度都為0。以FR 腿為例，建立坐標系{D}描述足端位置參數，如圖5 所示。該圖以關節1為坐標原點，機器人前進方向為x軸，豎直向上為z軸。

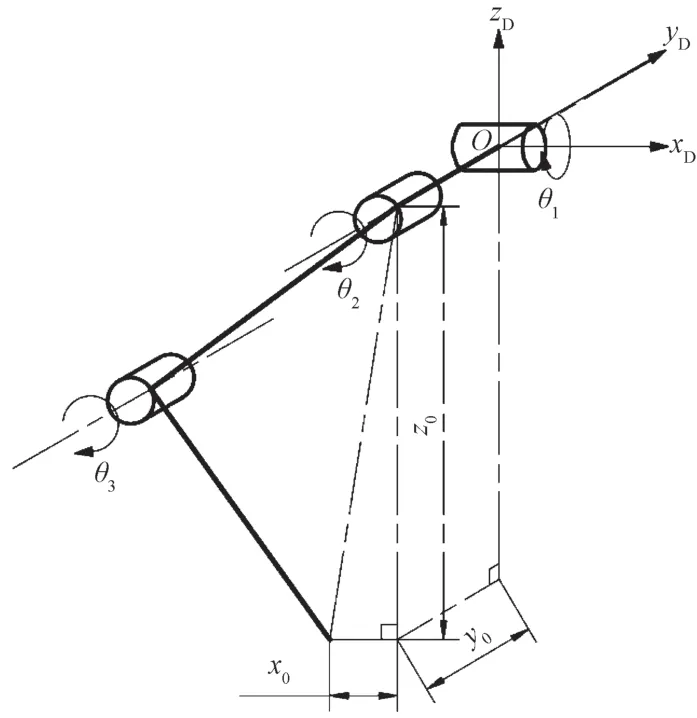
圖5 足端位置參數示意圖Fig.5 Schematic diagram of parameters of position of the extremities

機器人對角步態的時序圖如圖6 所示，設機器人初始機體質心高度為h。設步態周期為T，步長為S，抬腿高度為H，騰空率（理論擺動相占整個運動周期比率）為λ。

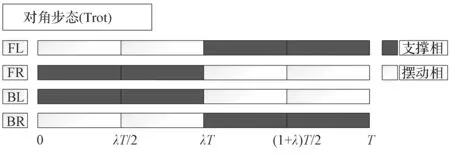
圖6 對角步態時序圖Fig.6 Trot gait timing diagram

設機器人足端初始位置為（x0，y0，z0）。由于機器人在y軸方向無運動，所以y0=-L1。顯然z軸足端初始位置的絕對值等于初始機體質心高度，即z0=-h。x0值的設定將對機器人運動的穩定性能有較大影響，后續仿真分析時將對x0值的設定進行詳細分析。

由于對角步態向前運動時關節1 不動，即θ1≡ 0，y(t)≡-L1。只需給出x軸和z軸方向上的約束。根據上述原則，得到每個周期T內，前進方向足端約束：

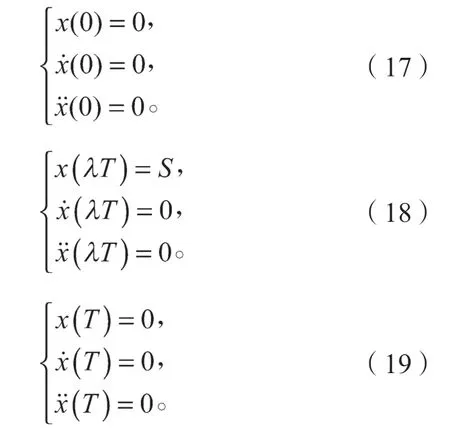
豎直方向足端約束：

3.2 足端軌跡函數

基于約束方程（17）～（23），擺動相足端軌跡擬采用復合擺線的形式。參考文獻[14]給出的擺動相足端軌跡為

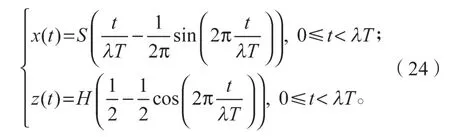
由足端軌跡求導計算出速度、加速度曲線可知：在z軸方向，t=0，t=λT時，加速度不符合約束方程（19）、（21），所以需要對z軸方向軌跡進行優化。優化后的擺動相足端軌跡函數如下：

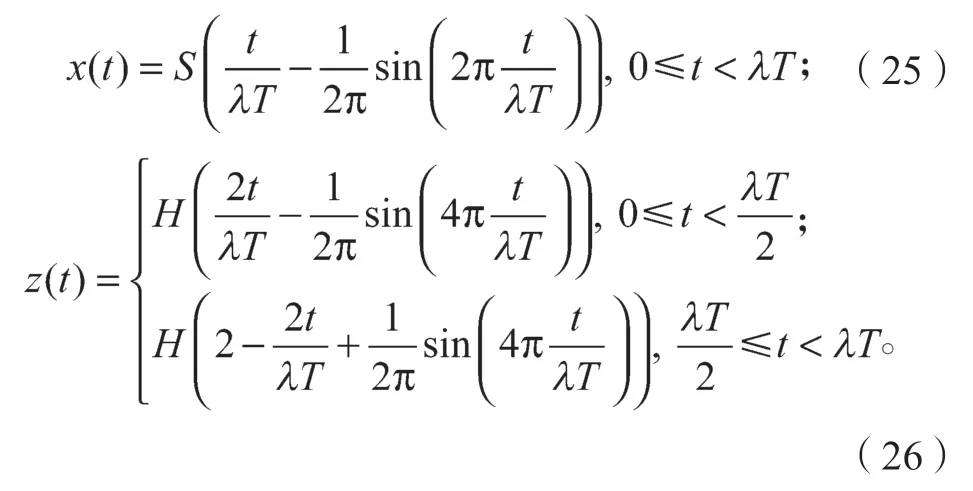
得出擺動相足端軌跡后，根據約束方程，容易得到支撐相足端軌跡方程為

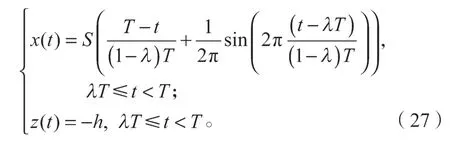
可根據實際情況調整步態周期T、步長S、抬腿高度H。實際使用時，足端軌跡函數還需加上足端初始位置（x0，y0，z0）的設定值。

4 Simulink 仿真分析

4.1 三維實體模型的建立

以優寶特“YOBOGO”型四足機器人為物理模型，根據其實際尺寸和質量，結合正向運動學公式（1），在SolidWorks 軟件中建立三維實體模型，見圖1。用基于SolidWorks 的SW URDF Exporter 插件導出URDF（unified robot description format）文件，該文件是一種機器人描述文件，在機器人系統里大量使用。也可用于各種仿真平臺內搭建機器人仿真模型。

4.2 Simulink 仿真模型的建立

將上一步生成的URDF 文件導入Matlab/Simulink仿真軟件中，并將足端軌跡函數，式（25）～（27），輸入相應的Simulink 模塊中，生成足端軌跡信號；并結合上文中給出的逆向運動學方程式（16）與Simulink 模塊解出的關節角度信號，從而對機器人的實體模型進行仿真控制。

Simulink 仿真運動過程如圖7 所示。圖7a 為一個周期T=0.500 s 的運動。t=0 s 時為四足機器人初始狀態，t=0.125 s 為一組擺動相運動狀態；t=0.250 s 擺動相與支撐相切換；t=0.375 s 為另一組擺動相運動狀態。圖7b 為4 個周期的運動。t=0.5, 1.0, 1.5, 2.0 s 分別為4 個周期的初始狀態。

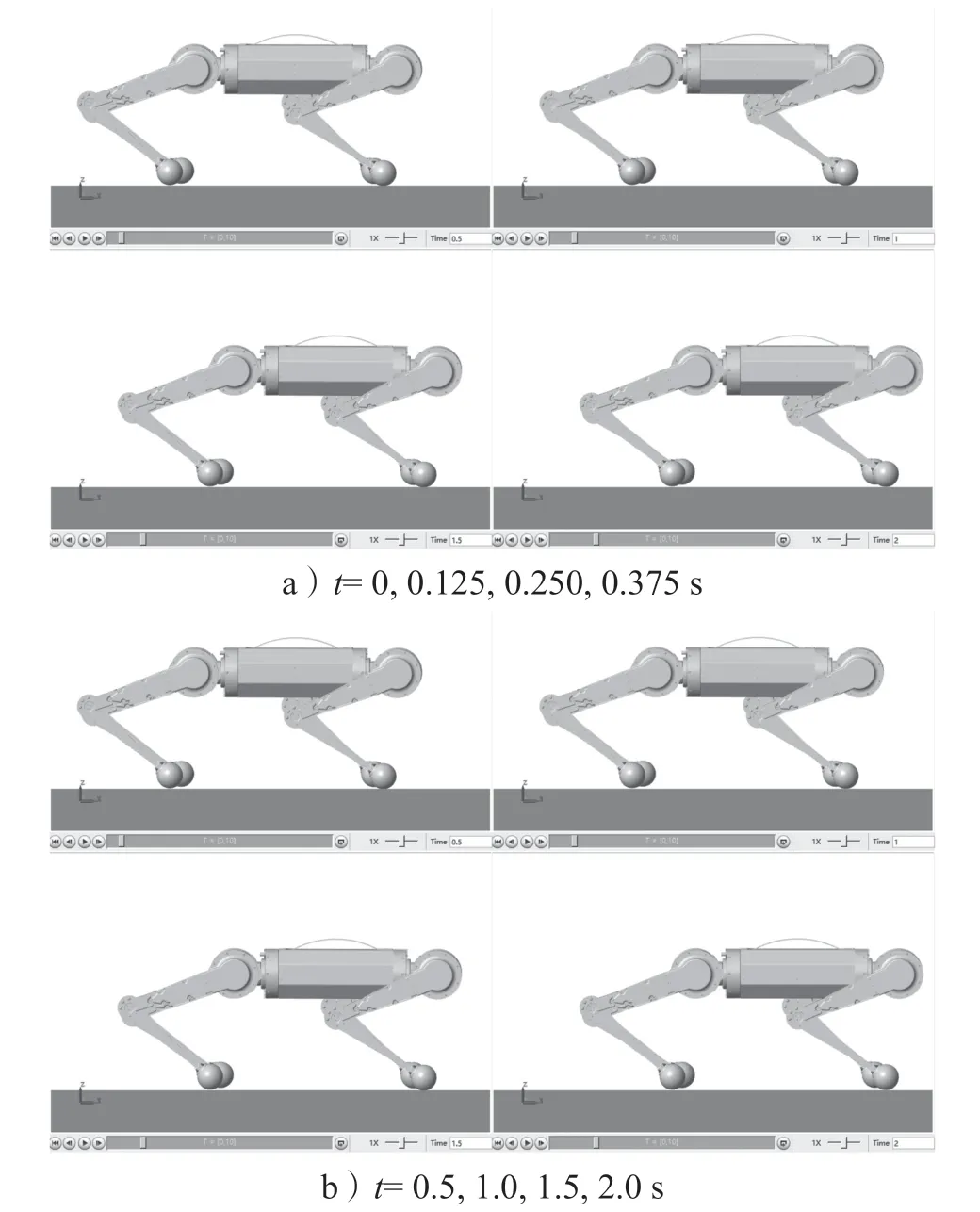
圖7 Simulink 仿真運動過程示意圖Fig.7 Diagram of simulink simulation movement

4.3 仿真條件設置

為了分別驗證四足機器人足端軌跡、足端初始位置對運動穩定性的影響，本研究進行了如下兩組對比仿真實驗。

實驗一：設定變量為足端軌跡，選取文獻[14]中給出的足端軌跡函數為優化前軌跡和優化后的足端軌跡，以此形成對比。

實驗二：采用優化后的足端軌跡函數，設定變量為足端初始位置。

四足機器人由于自身機體、腿部的重力慣性等因素，當進行對角步態行走，抬起對角兩條腿時，會向另一對角傾斜，造成對角步態兩條腿不能同時著地，從而增大足端與地面沖擊力造成運動的不穩定性。而初始足端位置的選擇將極大影響對角傾斜方向和大小。所以這里對四足機器人對角步態的足端初始位置進行仿真分析。四足機器人向前運動時，x軸方向足端初始位置對機器人穩定性影響最大，y軸方向可不動，z軸方向決定的是機體質心高度，需根據實際使用需求選取。所以本文主要對x軸方向足端初始位置變化進行仿真對比。

實驗中需設定的參數有：周期T，步長S，抬腿高度H，騰空率λ，足端初始位置x0、y0、z0。結合四足機器人腿部連桿長度參數：L1=76 mm，L2=210 mm，L3=210 mm。兩組對比實驗中均設定：周期T=0.5 s，步長S=20 mm，抬腿高度為10 mm，騰空率λ=0.5（即FL、BR 腿運動周期與FR、BL 腿運動周期相位差為0.5T）。實驗一足端初始位置為x0=-40 mm，y0=-76 mm，z0=-200 mm。實驗二足端初始位置變化范圍為-70～0 mm，每間隔10 mm 取值進行仿真，一共仿真8 次，y0=-76 mm，z0=-200 mm。

實驗中四足機器人先邁FL、BR 腿。每個實驗均仿真5 s，10 個周期。

4.4 仿真結果分析

兩組對比實驗分別從足端沖擊力F，機體質心位移x、y、z，機體俯仰角（pitch）φ、滾動角（roll）ω、偏航角（yaw）κ等具體數值來評價四足機器人的運動穩定性能。仿真在0 s 時刻時，機器人此時是懸空的，距離地面有微小高度，以及機器人本身慣性所致，前幾個運動周期會有不規律的現象。因此，以下數據分析皆不考慮前3 個不規律周期。

4.4.1 實驗一結果分析

在實驗一中，對比的是優化前和優化后足端軌跡對四足機器人運動穩定性的影響。影響結果如圖8 所示，由圖8 可以看出，優化后軌跡的足端沖擊力小于優化前軌跡的足端沖擊力。

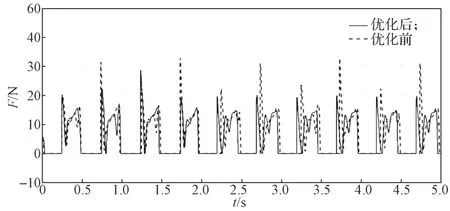
圖8 優化前后實驗一足端沖擊力變化曲線Fig.8 Impact force curves at the extremity of the first experiment of before and after optimization

圖9 為機體的質心位移曲線，從圖9 可以看出，5 s 仿真時間內：在x軸方向，優化后前進更遠；在y軸方向，優化前有較大偏移位移，優化后y軸偏移較小，前進方向更準確；在z軸方向，優化前后差距不大。

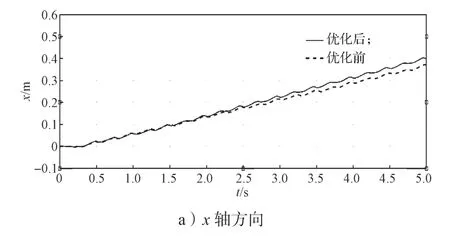
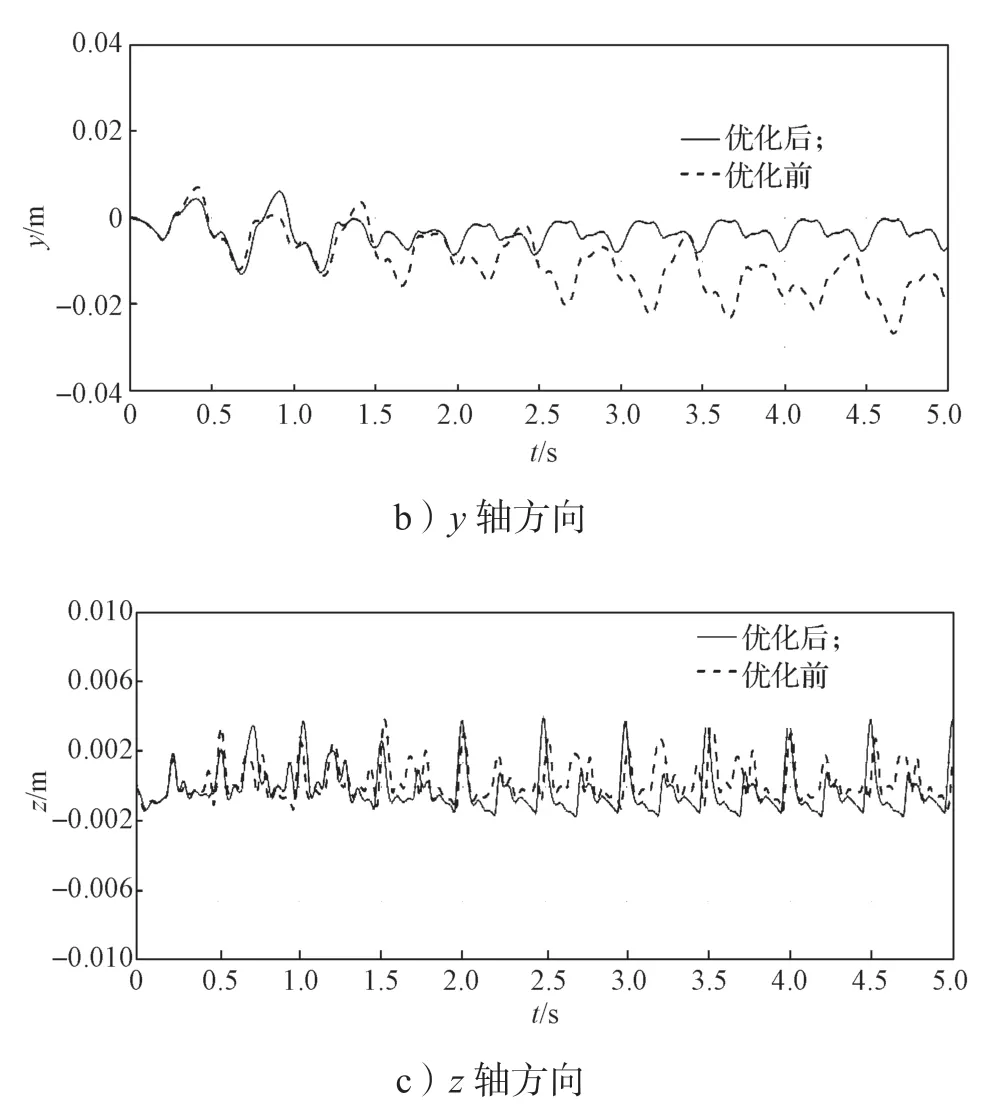
圖9 優化前后實驗一機體質心的位移變化曲線Fig.9 Mass center displacement curves of body in the first experiment of before and after optimization

機體質心位移的變化角度如圖10 所示，根據圖10 歐拉角的變化曲線可以知道，優化前俯仰角φ、滾動角ω都比優化后的波動大。優化后的偏航角κ比優化前更小。

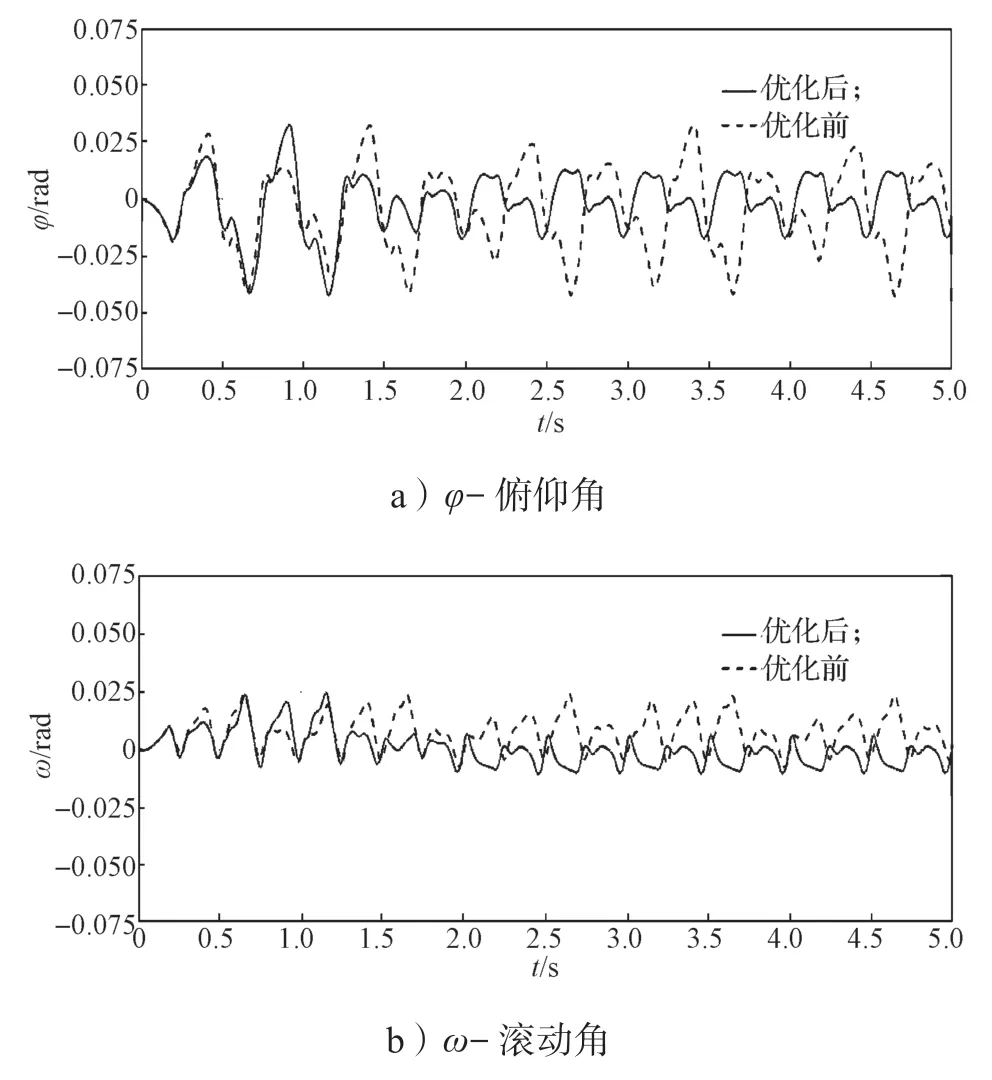
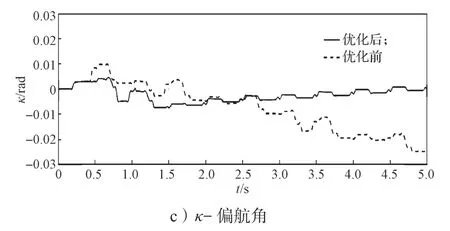
圖10 優化前后實驗一機體質心歐拉角的變化曲線Fig.10 Mass center Euler angle variation curves of body in the first experiment of before and after optimization

綜上對實驗一優化前、后軌跡的各種仿真曲線的分析，可以看出優化后足端與地面沖擊力較小，機體俯仰角、滾動角較小，運動較為穩定，優化后偏航角也變小，前進方向更準確。

4.4.2 實驗二結果分析

在實驗二中，對比的是足端初始位置x軸方向的變化對四足機器人運動穩定性能的影響。四足機器人穩定向前運動時，足端沖擊力F越小越好，x軸方向位移越大越好，y軸方向位移也是更小為宜。故上述3 個評價標準給出其仿真數值變化的最大值，見表2。分析表2 的數據可知，當x0=-40 mm 時，足端沖擊力F最小，為19.9 N；x軸方向的位移最大，為0.402 m；y方向的偏移最小，為-1.32×10-2m。

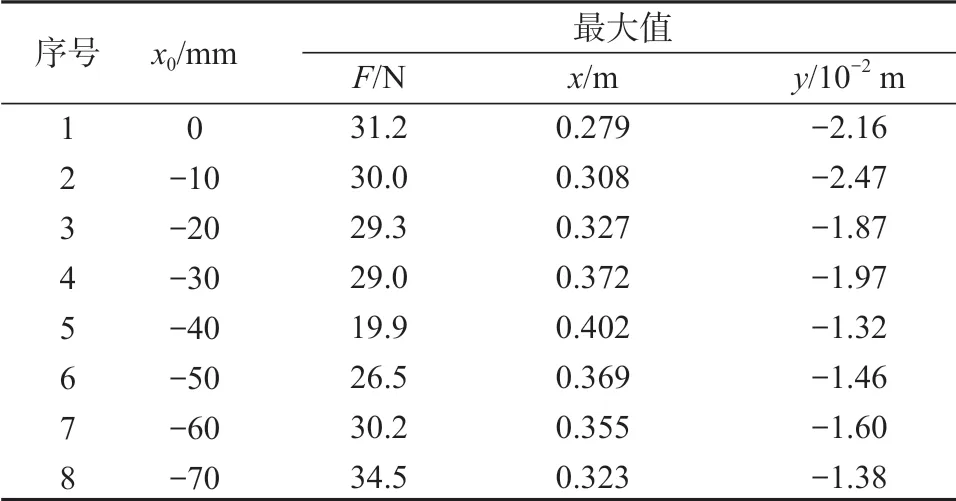
表2 實驗二F、x、y 隨x0變化的最大值Table 2 Maximum change of F, x and y in the second experiment as a function of x0

而z軸方向有地面作為約束，理論位移變化越小越好。同理，俯仰角φ、滾動角ω、偏航角κ亦是變化越小，四足機器人運動越穩定。因此，本研究給出上述評價標準的仿真數值變化的方差，如表3 所示。結合表2 和表3 可知，當x0=-40 mm 時，φ、ω的方差最小；當x0=-30 mm 時，z、κ的方差最小。

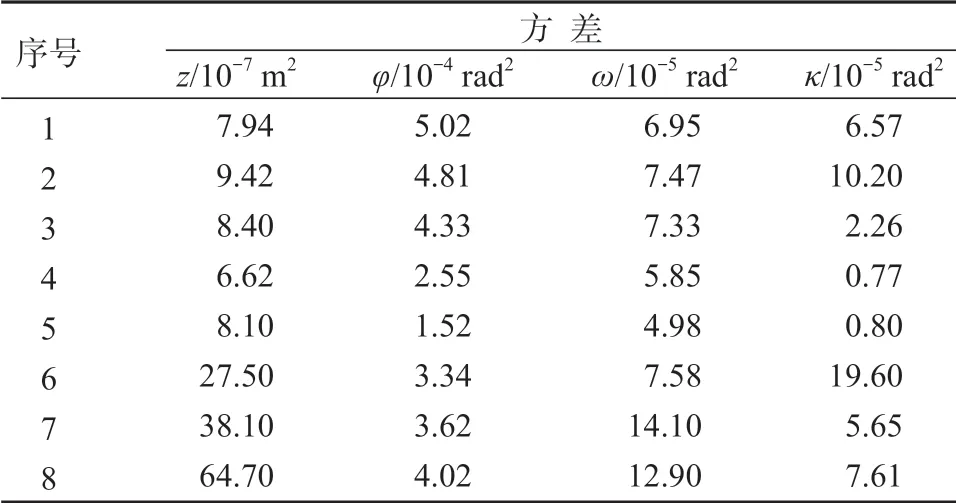
表3 實驗二中z、φ、ω、κ 的方差Table 3 Variance of z, φ, ω and κ in the second experiment

在四足機器人的對角步態仿真過程中，根據仿真視圖可以看出：當x0≥-40 mm 時，四足機器人有向后傾倒的趨勢，后腿先于前腿著地。x0≤-50 mm時有向前傾倒的趨勢，前腿先于后腿著地。機器人前腿先著地時明顯不如后腿先著地運動穩定。結合上述7 項數值的對比，可以看出當x0=-40 mm 時，各項數據都較為理想。由于篇幅限制，這里僅列出x0=-40 mm 以及x0=0 mm 兩次仿真數值的變化曲線，詳細對比不同初始足端位置對機器人穩定性的影響。以下將足端初始位置x0=-40 mm 稱為位置一；x0=0 mm 稱為位置二，仿真結果如圖11～13 所示。

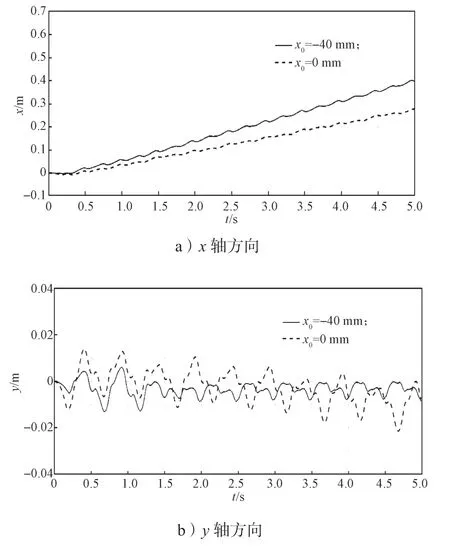
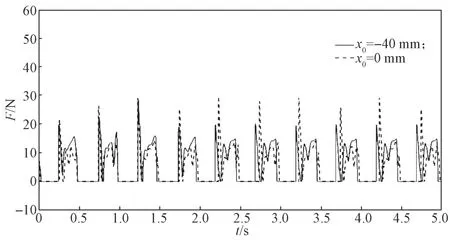
圖11 實驗二不同初始位置下足端沖擊力變化曲線Fig.11 Impact force variation curves at the extremity of the second experiment at different initial positions

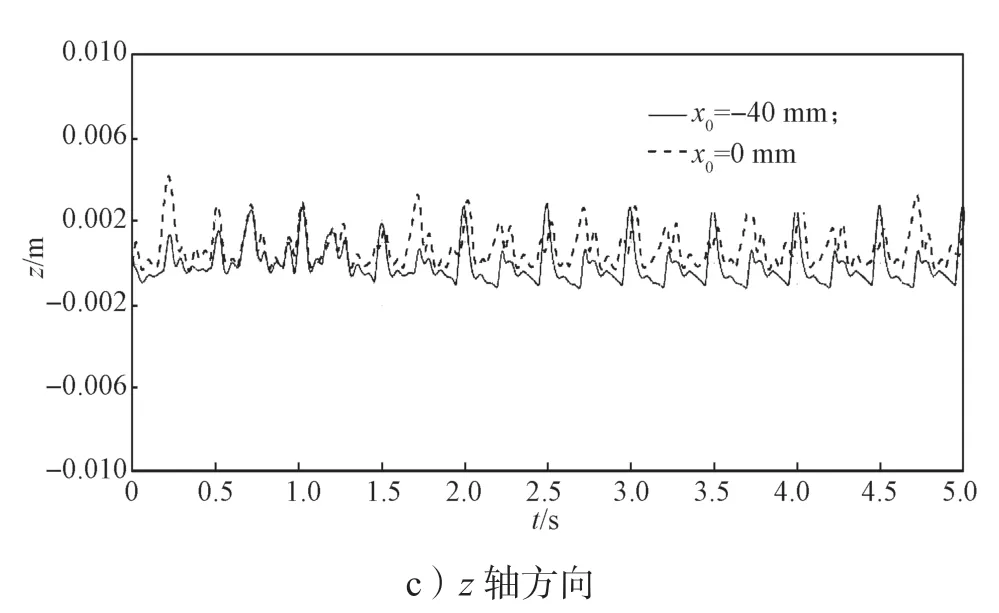
圖12 實驗二不同初始位置下機體質心的位移變化曲線Fig.12 Mass center displacement variation curves of body in the second experiment at different initial positions

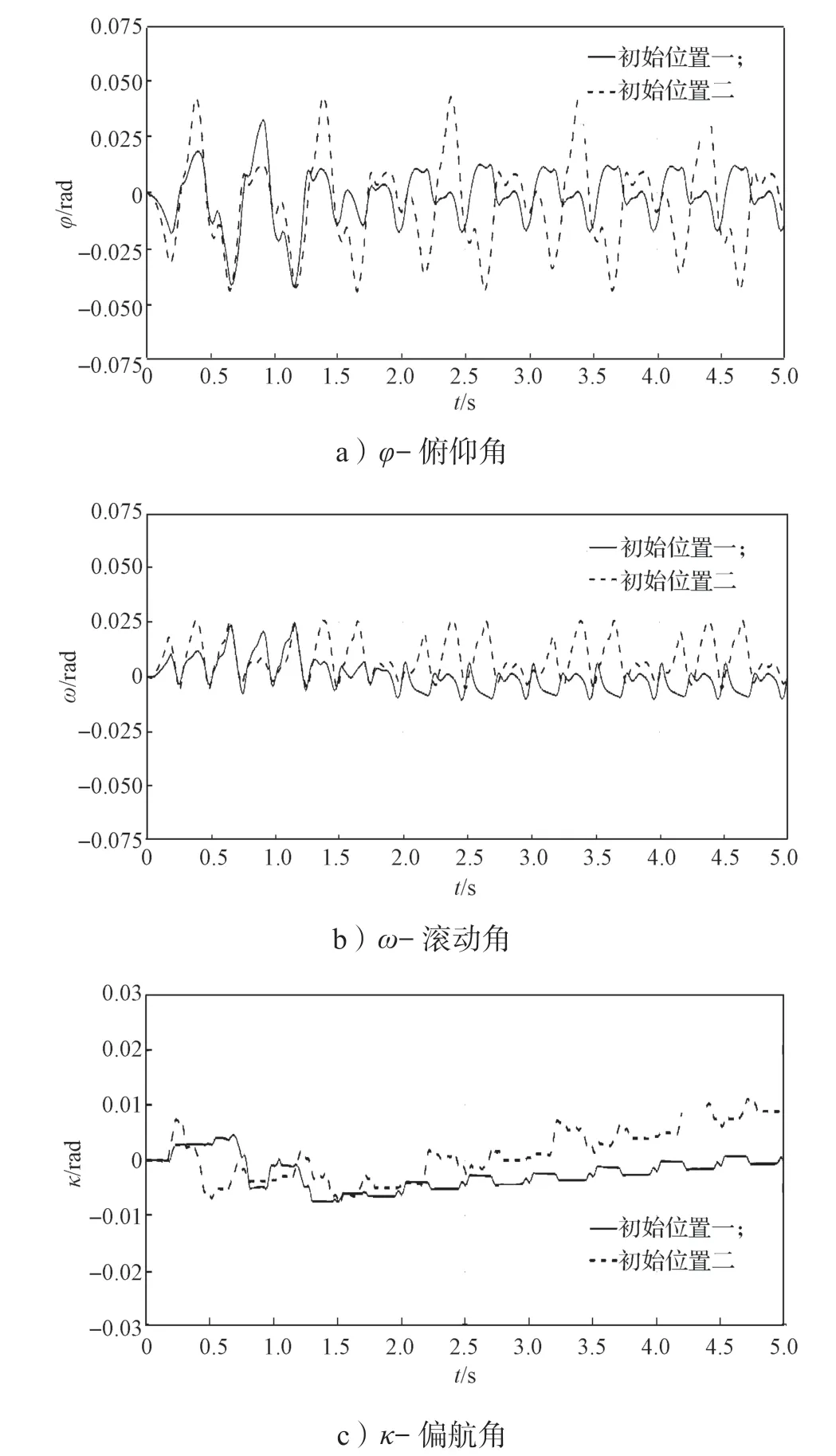
圖13 實驗二不同初始位置下機體歐拉角變化曲線Fig.13 Euler angle variation curves of body in the second experiment at different initial positions

由圖11 可知，位置一的足端沖擊力較小。由圖12 可知：x軸方向，位置一的位移較遠；y軸方向，位置一的波動較小；位置二有向y軸負方向位移的趨勢；z軸方向，兩位置波動差距相當。由圖13 可知，位置一的角變化較小，較為穩定，而位置二俯仰角φ、滾動角ω都波動較大，航偏角κ也有變大趨勢。

綜合實驗二對四足機器人足端初始選擇的仿真分析可得：當x0=-40 mm 時，足端與地面沖擊力較小，機器人前進較遠，機體俯仰角、滾動角波動較小，航偏角也較小。因此，此時四足機器人具有較優異的性能，運動較為穩定，前進方向較為準確。

5 結語

通過建立四足機器人正向、逆向運動學模型、基于足端零沖擊原則進行足端軌跡規劃，實現了四足機器人對角步態的運動；并且從足端軌跡函數、足端初始位置兩方面去優化四足機器人的對角步態；采用Matlab/Simulink 仿真實驗分析足端軌跡、足端初始位置對機器人運動穩定性的影響。仿真實驗結果表明，從足端軌跡、足端初始位置兩方面對機器人的對角步態進行優化規劃，使得機器人在運動過程中的穩定性能有較大的提高，實現了四足機器人有較為穩定的對角步態行走。