汽油辛烷值損失優化方案的數學建模與求解

陸天浩，李玲玲，陳宇峰，湯 瓊

0 引言

汽油的辛烷值作為汽油的商品牌號（例如89#、92#、95#），是衡量汽油發動機燃料抗爆性能優劣的重要指標。辛烷值越高，表示其抗爆性能越好，發動機壓縮比越高[1]。辛烷值的提高可以提升發動機功率，增加車輛行程；同時還能起到節約燃料，減輕使用者經濟負擔的作用。對于小型車輛而言，汽油是其主要的燃料，汽油燃燒產生的尾氣是影響大氣環境的重要因素。辛烷值反映了汽油的燃燒性能，然而當前的脫硫催化裂化汽油技術，使汽油的辛烷值大大降低。因此提高辛烷值是提高經濟效益和改善環境的一個重要手段[2]。

為了解決上述問題，針對“華為杯”第十七屆中國研究生數學建模競賽①本文為“華為杯”第十七屆中國研究生數學建模競賽二等獎論文。B 題：汽油辛烷值建模，將BP（back propagation）神經網絡模型與遺傳算法[3-8]引入預測與優化任務中，并通過預測優化找到符合條件的優化方案。

1 數據處理

1.1 數據預處理

用數學建模競賽B 題所提供的數據集作為原始數據集。在數據集中，共有325 個樣本，根據樣本采集時間排序，采集時間為2017-04—2020-05。每個樣本包含由原料性質、產品性質、待生吸附劑性質 、再生吸附劑性質等不同操作變量構成的354 個采集位節點。由于是原始數據，不同樣本中的不同位節點存在未采集數據或數據缺失等情況。如果不同樣本的同一位節點缺失數據較多，則該位節點不能準確反映變化情況，需要刪除該位節點。如果不同位節點的同一樣本數據較多，同樣需要刪除該樣本。對于缺失值個數較少的位節點，可根據臨近時間的樣本對應位節點值進行填充。再對篩選后的數據采用3σ準則去除異常值；根據實際應用背景確定取值范圍，將超過范圍的位節點或對應樣本數據剔除。具體數據處理如下。

1）遍歷整個數據表，將采集值缺失過多的樣本及位節點刪除。經過篩選，共刪除12 個位節點，具體名稱如表1 所示。這類位節點由于信息缺失過多，因此不能清晰體現該位節點對辛烷值損失的影響。

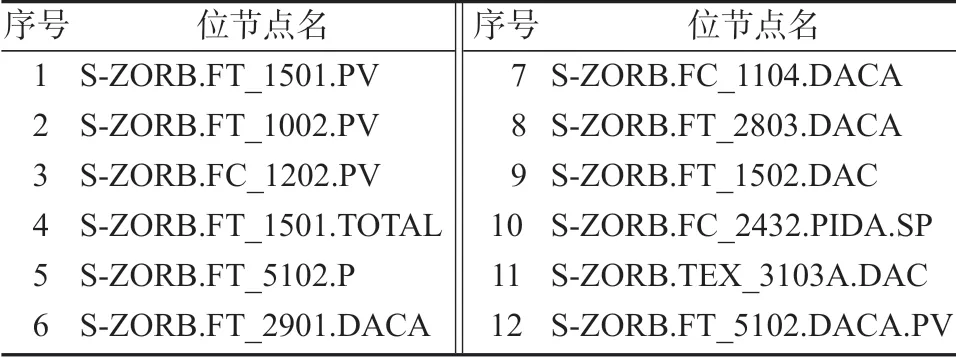
表1 第一步被刪除的位節點Table 1 Removed sites in the first step

2）對位節點進行過濾操作，刪除數值全部為空值或無法通過相鄰樣本進行填充的位節點。前者沒有數值變化，不能體現該位節點對辛烷值損失的影響。后者只有部分時間段樣本，不能完整地體現該位節點對辛烷值損失的作用。過濾后，刪除19 個位節點，具體名稱如表2 所示。

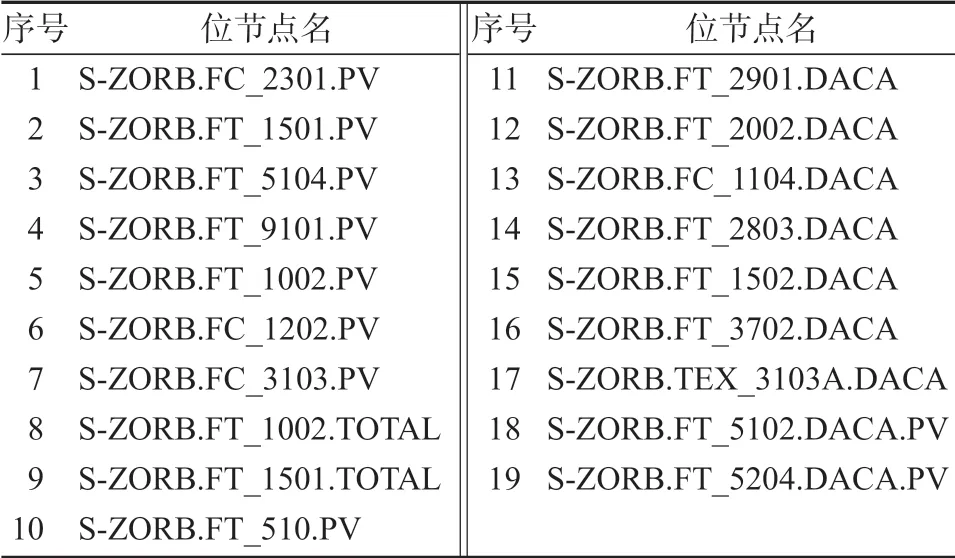
表2 第二步被刪除的位節點Table 2 Removed sites in the second step

3）對于存在少量空缺值的位節點，用相鄰樣本的均值進行填補，需要補充的位節點如表3 所示。

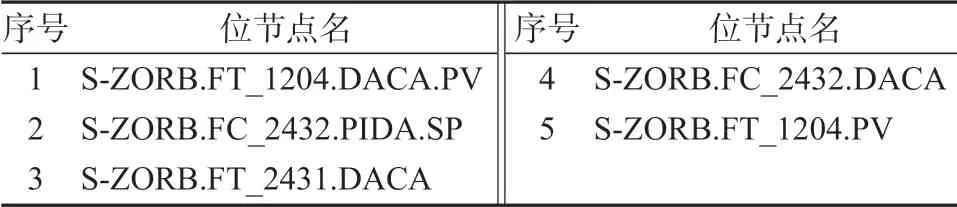
表3 缺省值填補位節點Table 3 Nodes filled by the default value

4）根據不同操作變量實際取值范圍，剔除位節點采集值異常的32, 29, 27 號樣本。

5）使用3σ準則去除異常值及其所帶來的影響。

完成上述預處理后，將285, 313 號樣本結果加入到對應位置。

1.2 數據降維

模型1 主成分分析

主成分分析法是使用線性降維的方法來尋找模型的主要操作變量，以達到精簡影響因素數量的目的。本文使用SPSS 進行主成分分析，使多維的數據降維得到少數幾個綜合指標，具體操作步驟如下：

1）數據標準化

設x1,x2,…,xm為m個主成分分析變量，aij為m個評價對象中第i個評價對象對應于第j個分析變量的取值。將每個aij值標準化，

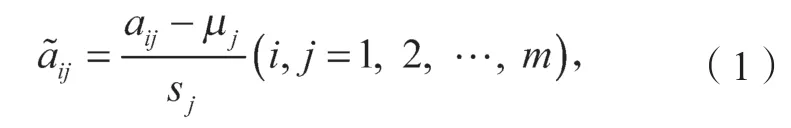
標準化指標變量，即

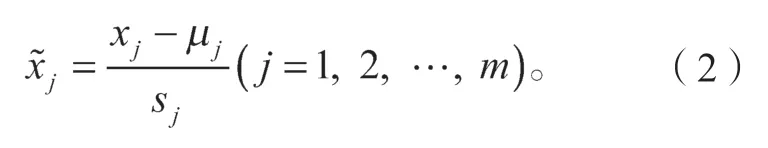
2）計算數據的相關系數矩陣

相關系數矩陣R的具體表達式為

式中，rpq為第p個指標與第q個指標之間的相關系數，且

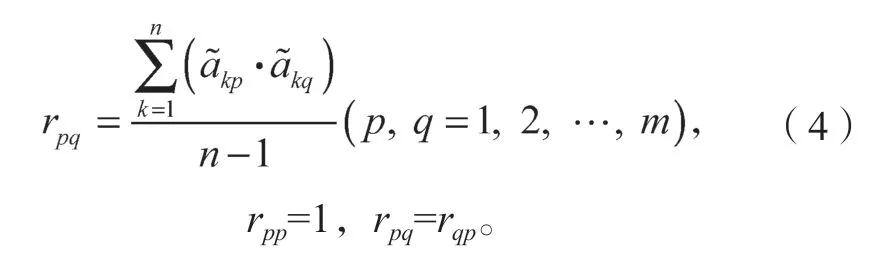
使用主成分分析法對數據集中的320 個位節點進行分析。第一次實驗中，將主成分個數設置為25，共篩選出200 多個變量。但由于決定主成分因子的操作變量種類各不相同，在工藝和設備操作上沒有很強的關聯性。因此將主成分個數設為5，然后重新實驗，結果如下：反應過濾器壓差，反應器上部溫度，SZORB.FT_9001.TOTAL，SZORB.FT_5201.TOTAL，SZORB.FT_9102.TOTAL。第二次實驗結果優于第一次，但由于傳統方法的關聯模型變量少、要求高，因此響應慢、效果差，且5 個主成分因子只能解釋59.374%的結果。

總的來說，通過對位節點進行降維，可以得到一部分主要操作變量。但是由于操作變量之間具有高度非線性和相互強耦合的關系，使用主成分分析法篩選出的主要操作變量影響因子較低，不具有很強的解釋性，因此本文采用非線性的降維方法。

模型2 層次聚類法

由于數據集中的320 個有效位節點之間具有高度非線性和相互強耦合關系，為了尋找具有代表性和獨立性的主要操作變量，再采用非線性的層次聚類法進行篩選。最后將主成分分析與層次聚類法篩選出的結果進行綜合分析，得出最終建模需要的主要操作變量。構建過程如下：

參考歐幾里德距離評價，在數據不規范時，皮爾遜相關系數會給出更好的結果，故本文使用皮爾遜相關系數來尋找模型的主要操作變量。具體算法見式（5）（6）。

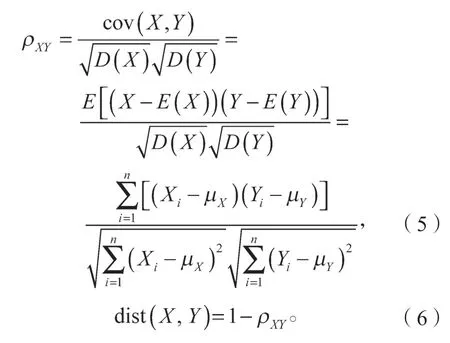
式（5）（6）中：X、Y為兩個不同的變量；

μX、μY和D(X)、D(Y)分別為變量X、Y的均值和方差；

ρXY為兩變量X、Y間的皮爾遜相關系數，當2個變量完全匹配時，ρXY=1，當2 個變量毫無關系時，ρXY=0。

為了使相似度越大的兩個變量之間距離越小，采用1 與皮爾遜相關系數的差值來衡量[9]，見式（6）。

使用SPSS 進行層次聚類分析，再與主成分分析得到的結果綜合分析后，得到了13 個主要變量：氫油比、反應過濾器壓差、反應器上部溫度、反應器底部溫度、烯烴含量、芳烴含量、反應器頂低壓差、待生吸附劑性質（焦炭含量）、待生吸附劑性質（硫含量）、再生吸附劑性質（焦炭含量）、再生吸附劑性質（硫含量）、辛烷值和硫含量。結合工藝要求和操作經驗發現這13 個主要變量符合實際情況，并在后面的辛烷值損失模型建立和優化過程中，可呈現較好的效果，證明了這13 個主要變量具有有效性和代表性。

2 基于BP 神經網絡的辛烷值損失預測模型

反向傳播網絡可以擬合任何非線性函數，是可以實現從輸入到輸出的端到端網絡，而且訓練網絡的方法非常簡單、有效，只需要學習網絡參數即可。通過數據預處理與數據降維，將13 個主要變量作為神經網絡的輸入進行訓練。基于BP 神經網絡的辛烷值損失預測模型網絡結構圖如圖1 所示[8]。神經網絡模型可分為兩部分：第一部分神經網絡有800 層，作為特征提取層；另一部分為單層全連接層，作為預測層。需要注意的是，在模型選擇時，輸入輸出的維數固定，中間的隱藏層部分需要考慮是否全連接。圖中的箭頭表示數據流動的方向，即模型的流程；w表示神經網絡中的權重矩陣，權重可通過訓練得到；B表示各層神經元的偏置，可以使模型具有更魯棒的表達能力。

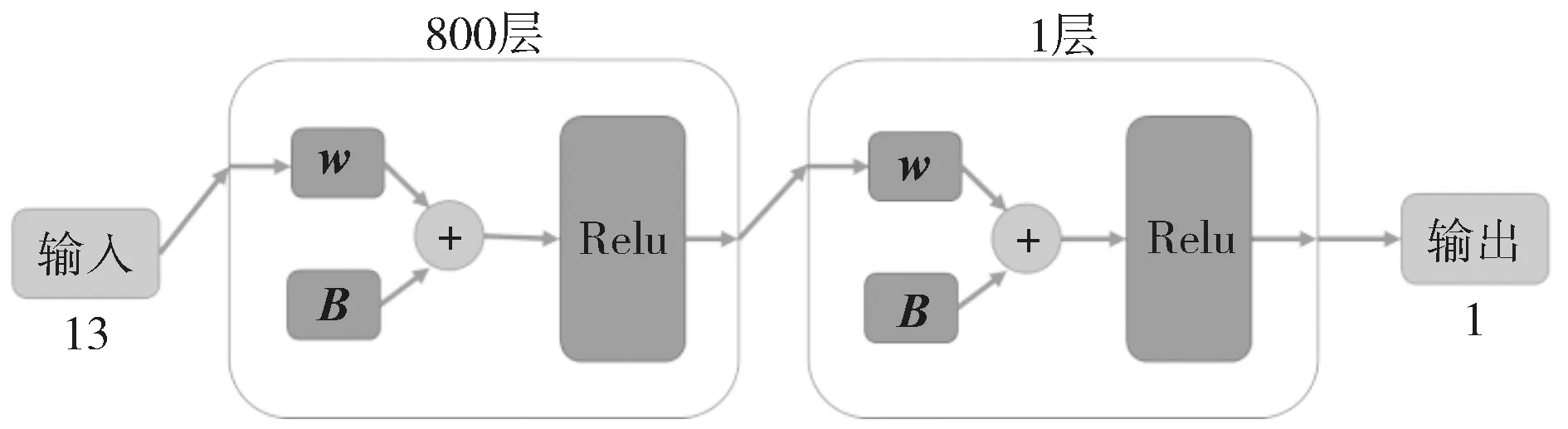
圖1 基于BP 神經網絡的辛烷值損失預測模型網絡結構圖Fig.1 Network structure diagram of octane loss prediction model based on BP neural network

模型（反向傳播梯度）在更新網絡參數時，為避免波動過大出現梯度消失或梯度爆炸現象，導致模型崩潰，需要對輸入進行零均值化與歸一化，使輸入數據的分布統一。經過歸一化，輸入被約束在[-1, 1]的區間內。

第一步零均值化

式中：xi為某一主要變量的某條樣本采樣值。

m為主要變量的樣本個數。

第二步歸一化方差

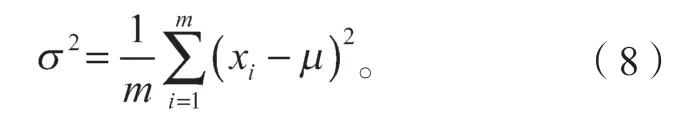
在神經網絡中添加激活函數，可以增加網絡的非線性表達能力，并解決線性模型不能很好描述的函數

關系[5]。神經網絡中所采用Relu 激活函數為

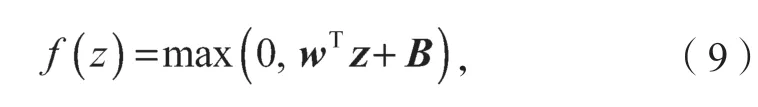
式中：z為激活函數的輸入，在本文的網絡中為激活函數前一層神經元的輸出；

B為對應層神經元的偏置（參見圖1）。

Relu 函數在正區間解決了梯度消失的問題，而且使神經網絡的收斂速度和計算速度較使用其他激活函數（如sigmoid 等）有明顯提高，起到了類似Dropout 的各層神經元隨機連接的效果。

考慮到神經網絡的輸入數據為篩選出的主要操作變量，故采用均方誤差（mean square error，MSE）來進行模型的評價。MSE 可以評價數據的變化程度，其值越小說明模型預測結果具有更好的精確度[6]，且具有較小的波動。具體表達式如下：

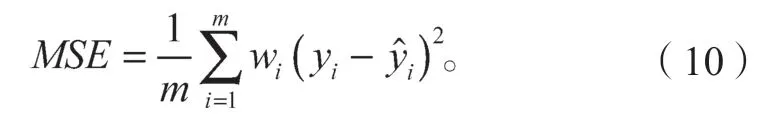
式中：yi、分別為辛烷值損失真實值和模型預測值；wi為神經網絡中各預測值的權重。

3 模型求解

在對神經網絡模型的實際訓練過程中，采用Adam 優化器進行梯度更新。相比于傳統的隨機梯度下降，Adam 通過計算梯度矩陣為各個參數設置更加靈活的學習速率，對變化頻繁的參數采用大步長進行學習，對于稀疏的參數采用小步長進行學習。第k步梯度gk更新如式（11）所示。

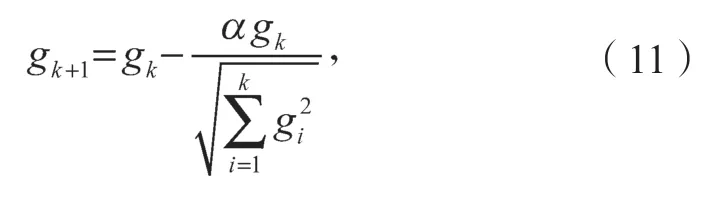
式中α為調節系數，用于調節變化快慢。

將整個數據集劃分為80%的訓練集和20%的測試集。測試集不參與模型訓練，在測試集上通過模型的預測結果來觀察模型的實際泛化能力。經過2 048 Epochs 訓練，模型的損失函數變化如圖2 所示。

由圖2 可知，隨著訓練次數的增加，在測試集上的損失值逐漸降低，在2 000 次左右達到了9.928×10-6，這說明模型有良好的泛化性能。

圖2 損失函數的變化圖Fig.2 Change diagram of the loss function

以損失函數的變化作為本研究中神經網絡預測模型的測試標準之一。使用Matlab 軟件建立網絡的訓練參數如下：迭代次數為2 048，學習率為0.01。訓練時模型參數的變化如圖3所示。由圖3a可以看出，隨著epoch 的增加，模型梯度逐漸減小，變化趨勢逐漸穩定。圖3b 可以看出在訓練時沒有出現模型崩潰現象，具有很好的穩定性。

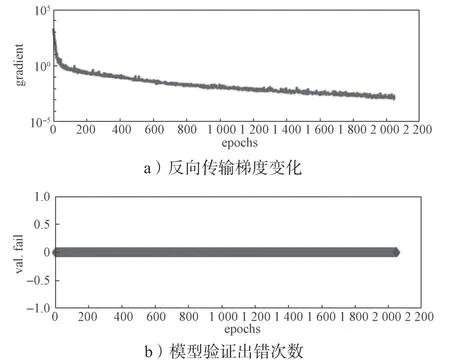
圖3 訓練時神經網絡模型參數變化圖Fig.3 Neural network model parameter variation diagram during training

經過訓練，訓練模型的最終回歸結果如圖4 所示。由圖4 可以看出，目標值和輸出結果基本上在直線y=x附近分布，說明訓練結果比較理想。

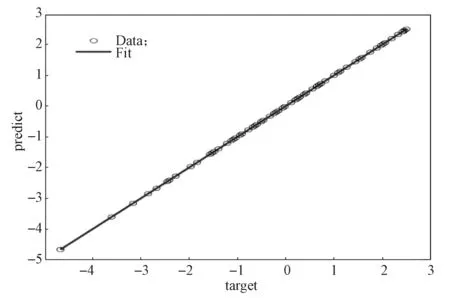
圖4 模型的回歸結果Fig.4 Regression results of the model

圖5 為各樣本的辛烷值損失實際值與預測值的分布情況。由圖5 可以看出，模型擬合效果明顯，可以較好地表達辛烷值的變化情況，并且能取得很好的預測效果。

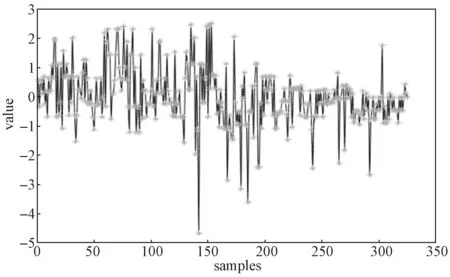
圖5 各樣本預測值與真實值分布圖Fig.5 Predicted value and true value distribution ofeach individual sample

圖6 為3 509 次迭代的損失函數變化圖。由圖可以看出，在訓練2 000 次以后，損失函數下降趨勢基本趨于穩定，與圖2 中2 048 次迭代的結果相比，MSE在預測和訓練上的變化區別不大，擬合程度較高，這說明模型具有良好的有效性和泛化能力。

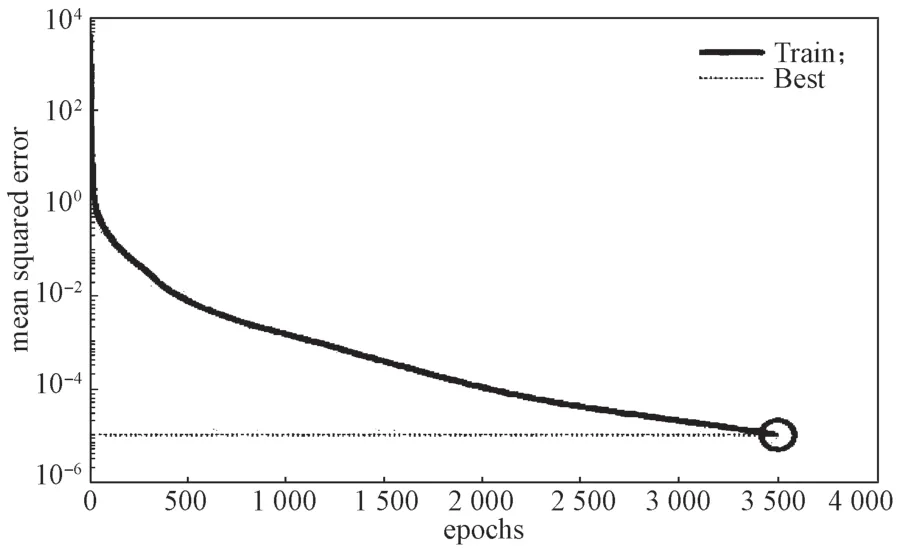
圖6 3 509 次迭代損失函數變化圖Fig.6 Loss function variation diagram for 3 509 iterations

4 基于遺傳算法的方案優化

遺傳算法是一種隨機化搜索方法，是一種模擬達爾文進化論和孟德爾遺傳學機理的計算模型。遺傳算法由編碼、適應度評估和遺傳運算3 部分組成[7]。根據損失散點圖，將損失變化通過三角函數進行擬合，即可得到每一個樣本的損失值。由于每一個樣本包含13 個主要操作變量，損失值可以由操作變量表達，在此可將問題轉變為基于主要操作變量的曲線優化問題。利用遺傳算法解決多元非線性回歸問題，并向最小化損失值的方向優化，得到13 個主要操作變量的對應取值。根據變量的取值范圍，得到對應主要變量的優化操作條件。

對于本問題，使用傳統方法難以獲得最優解，而多峰最優化問題具有多個局部解的特性，因此使用多峰非線性方法來求解，具體實驗參數設置如表4 所示。其中，自變量上下界用來表示每個主要操作變量取值范圍，交叉概率、變異概率用于控制個體改變頻率，設置迭代次數為1 000，使算法能夠得到足夠穩定的優化解。

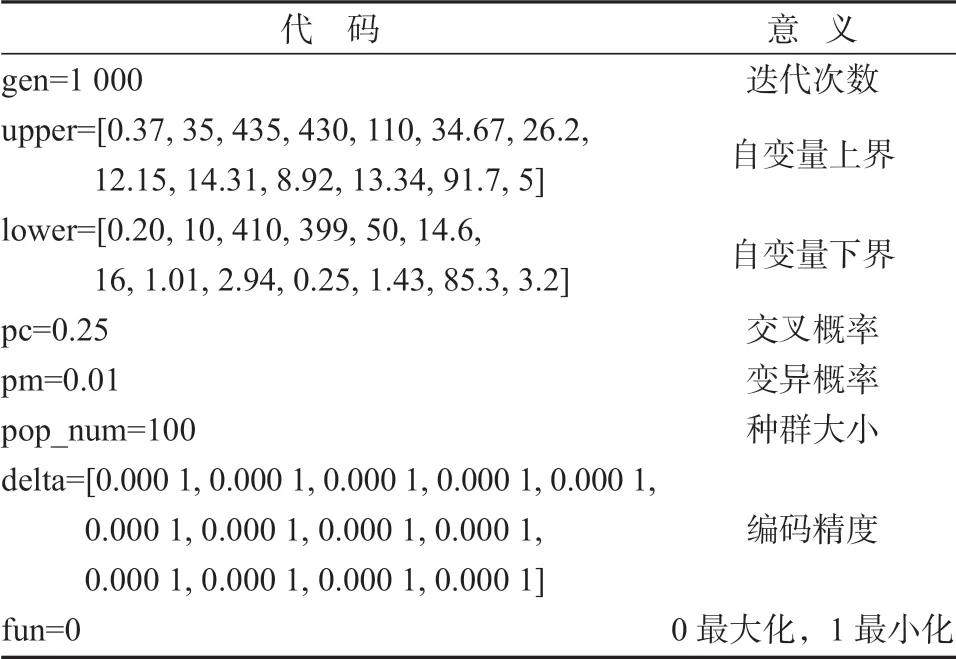
表4 實驗參數設置Table 4 Experimental parameter setting

經過實驗，遺傳算法的損失變化如圖7 所示。由圖7 可以看出，隨著迭代次數增加，損失的波動幅度逐漸減小，最終解逐漸趨于穩定。損失變化曲線表達式為

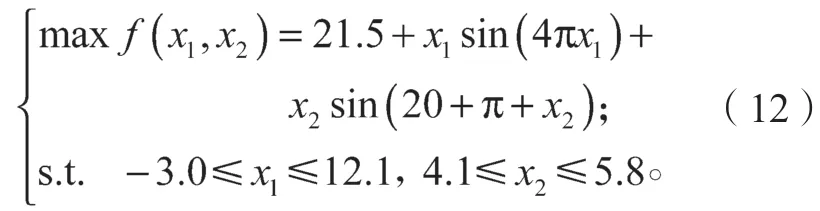
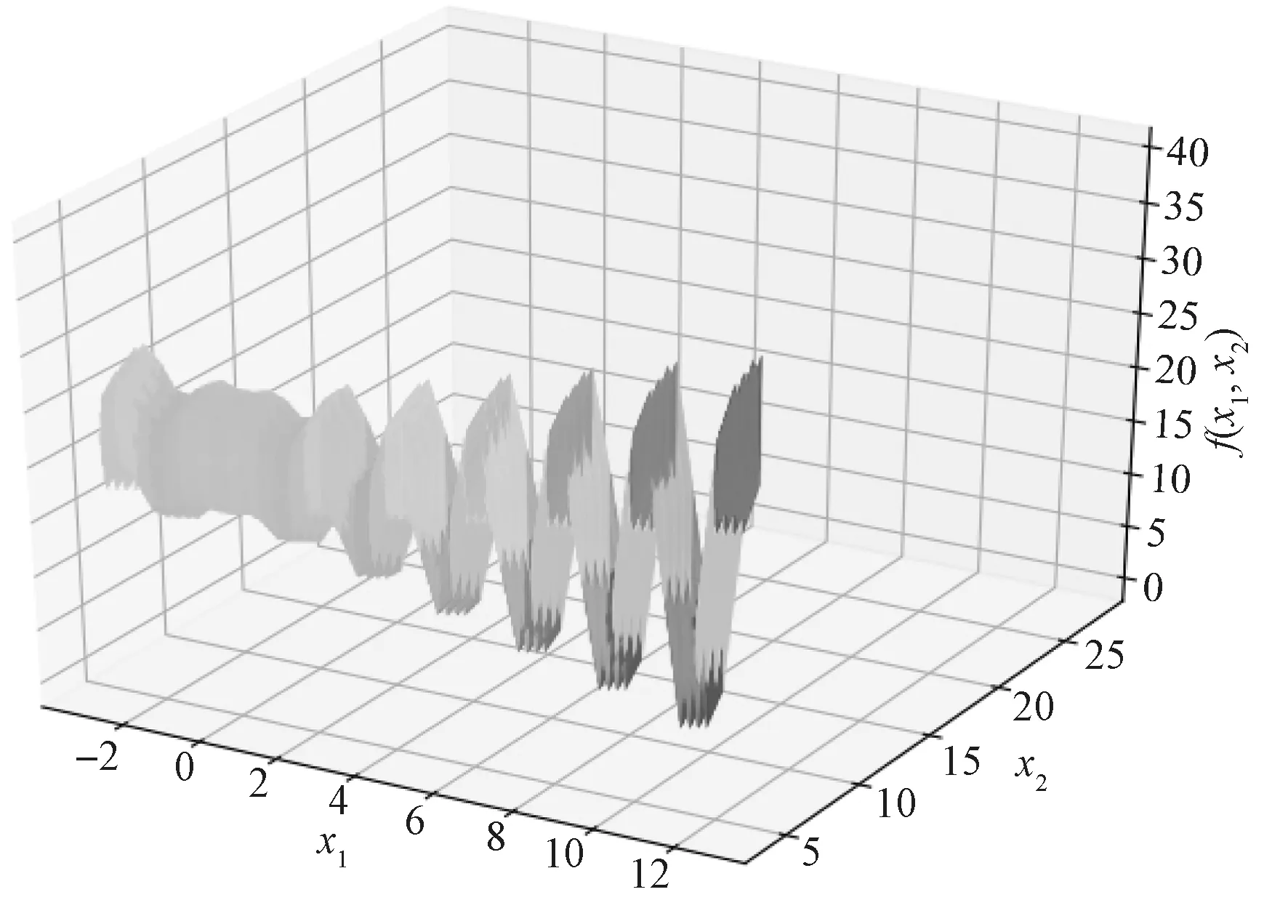
圖7 遺傳算法的損失變化曲線Fig.7 Loss change curve of genetic algorithm

遺傳算法最優個體得分曲線如圖8 所示。由圖8可能看出，遺傳算法在400 次迭代后每代最優函數值變化逐漸穩定，這證明算法已逐漸收斂于最優解。

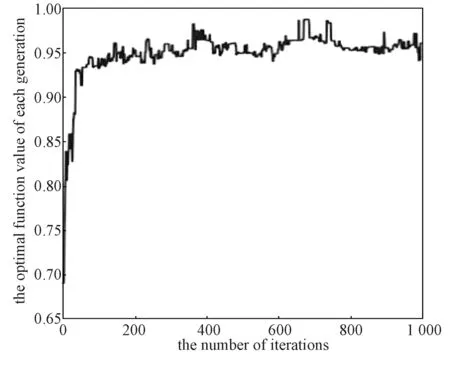
圖8 每代最優個體得分變化曲線Fig.8 Optimal individual score variation for each generation

通過上述遺傳算法，可以得到一批子代，每個子代對應一組變量。根據辛烷值損失值與13 個變量之間的關系，建立如下損失值與主要變量間的表達式：

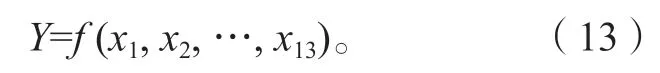
由于優化問題一般是從凸函數最小化尋找最優解，因此采取最小化f值的方式，獲得x變量的取值，x對應13個主要操作變量。經過遺傳算法的編碼解碼，從遺傳算法中選擇降幅大于30%的樣本，每個樣本對應主要變量優化后的一種操作條件。符合條件的優化方案，按照降幅比降序排列后，結果如表5 所示。當13 個主要變量分別優化至表5 首行對應數值時，所能達到的降幅比為44.822%，是所有得到的優化方案中的最優解。

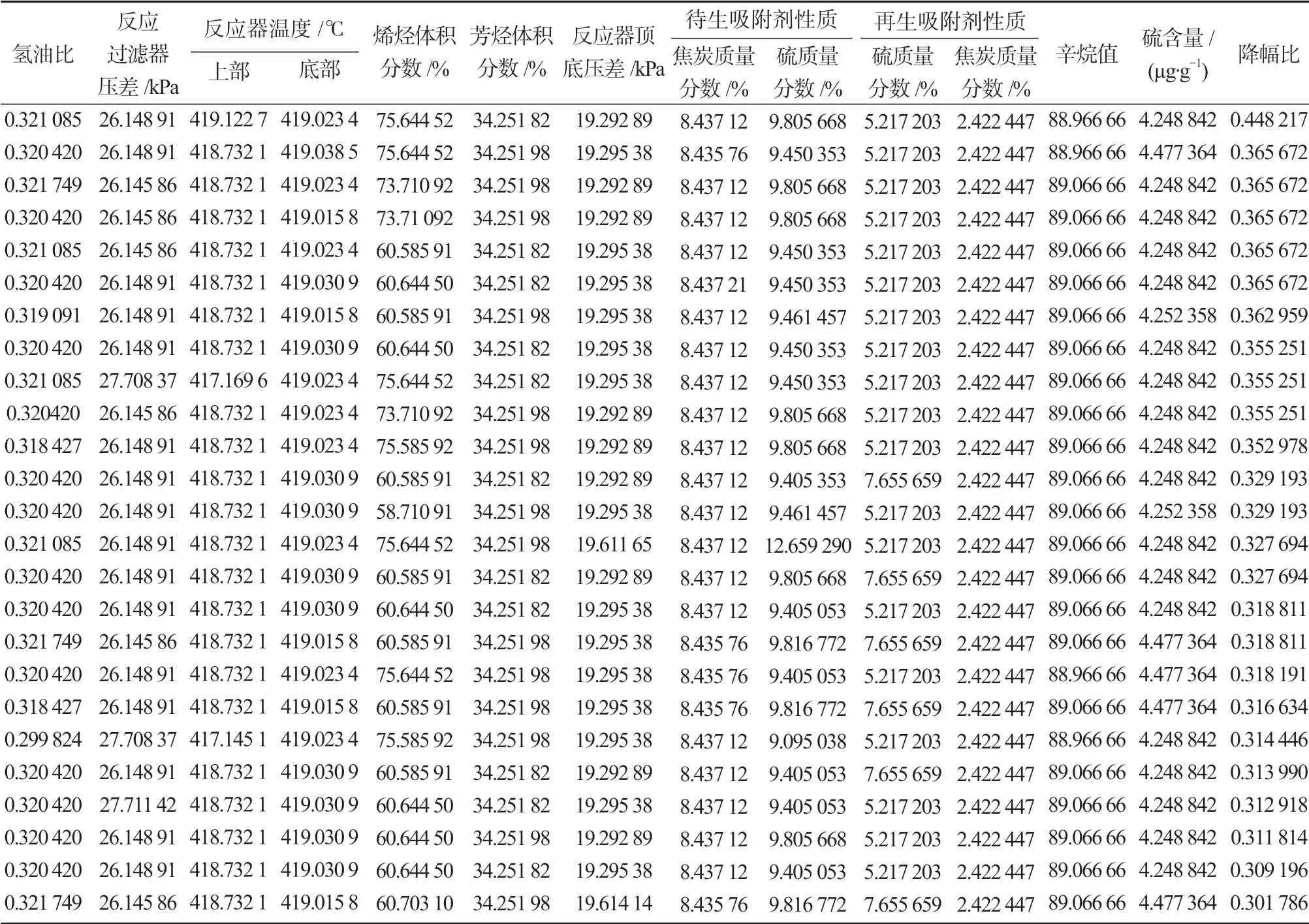
表5 符合條件的優化方案Table 5 Satisfactory optimized schemes

當某一變量逐步優化，其他變量不變時，辛烷值增加量與優化步數之間的變化情況如圖9a和9b所示。由于再生吸附劑性質硫優化迭代步數較多，因此通過圖9b 展示。由圖9 可以看出，辛烷值增加量的變化與氫油比、反應器底部溫度和反應器頂底壓差變化呈正相關；隨著變量反應過濾器壓差值越接近最優理想狀態，對辛烷值的影響變弱；辛烷值增加量變化與反應器上部溫度變化呈先負相關后正相關的關系，且變化趨勢大致相同，而待生吸附劑中的焦炭含量對辛烷值變化影響相反；辛烷值增加量與烯烴含量變化呈不斷抖動的影響關系，正負相關性交替出現；辛烷值增加量與芳烴含量呈近似指數變化的正相關關系，且越接近最優狀態影響越明顯；再生吸附性質（焦炭含量）對辛烷值增加量產生不斷交替的正負相關性，但總體呈微弱的正相關性；辛烷值增加量與再生吸附性質（硫含量）呈倒二次函數變化趨勢；原材料對產品辛烷值增加量的影響呈現出負相關的特性，且隨著其值逼近最優值，對產品辛烷值增加量的負向影響力度愈加強烈。由圖9c 可知，當所有主要變量同時進行優化時，主要變量對辛烷值增加量的綜合影響可以分為兩個階段，從一開始的初始狀態到第10 次迭代，對辛烷值增加量的變化影響明顯；第10 次迭代之后，對辛烷值的影響雖然仍然是正相關，但其影響程度下降了很多，其中一個原因是有些變量已經達到最優解。

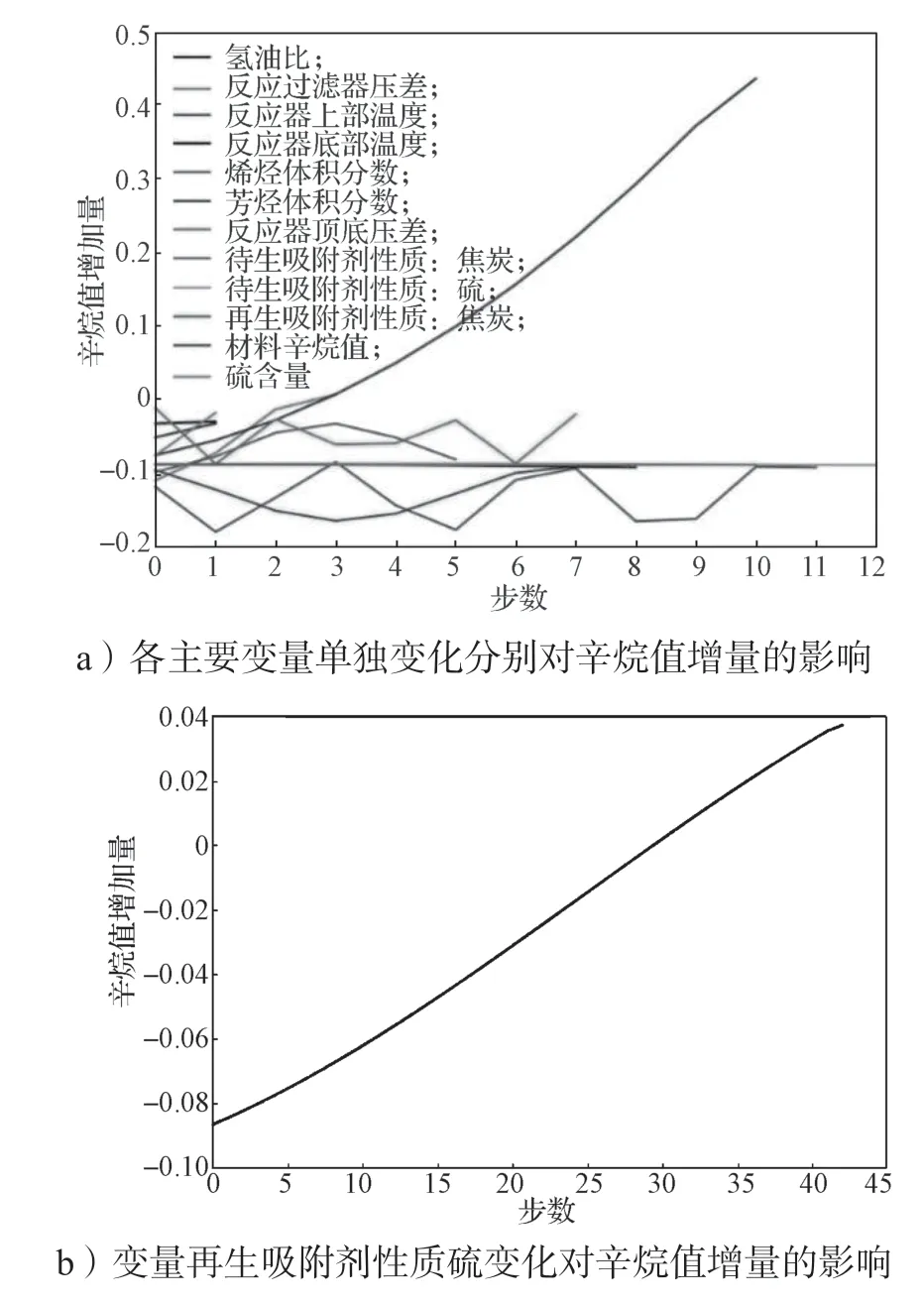
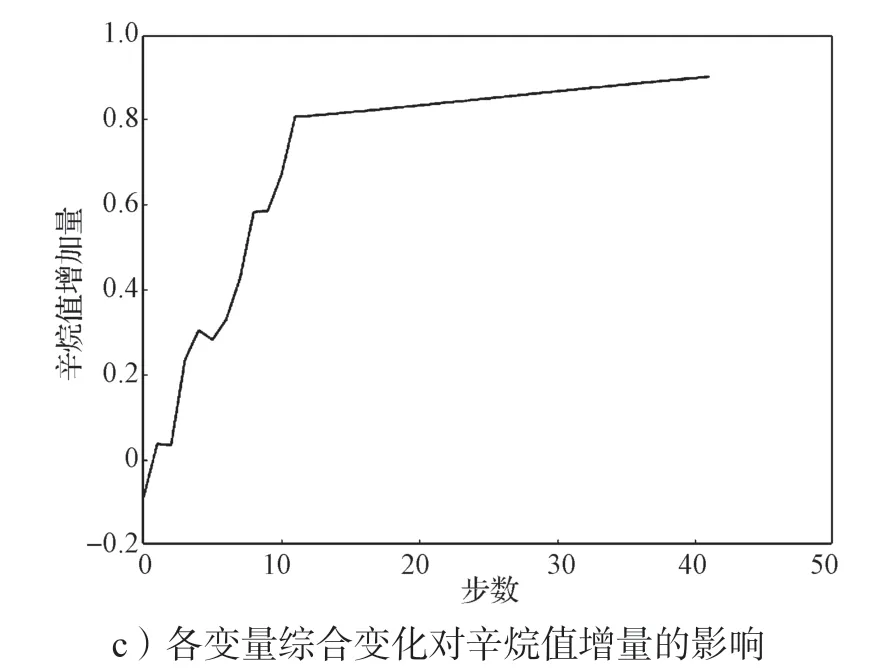
圖9 各主要變量變化及辛烷值增量變化軌跡圖Fig.9 Trajectories of major variables with their octane numbers

5 結語

本文通過層次聚類的方法，對預處理后的原數據集進行降維處理，建立基于BP 神經網絡的辛烷值損失預測模型，對辛烷值損失及其指標進行預測；使用遺傳算法迭代得出辛烷值損失降幅比大于30%的優化方案及最優優化策略，并通過可視化將各個操作變量的變化軌跡展示出來加以分析。實驗結果表明，使用非線性層次聚類法比使用線性聚類法效果更好，能夠很好地對數據集進行降維，降低了神經網絡模型的訓練與收斂難度。預測模型經過2 048 次迭代后，神經網絡模型的損失函數下降趨勢基本穩定。在數據集上，采用8:2 的比例構建訓練集和測試集，并在測試集上達到了9.982 6×10-6的誤差精度，能滿足模型預測的要求和精度。根據樣本硫含量不大于5 μg/g、主要操作變量的取值范圍，以及13 個主要變量的變化步長，利用遺傳算法迭代得到最優的參數集合。從集合中找到子代滿足辛烷值損失降幅比達到30%的樣本并排序，得到全部優化方案以及最優優化方案。在最優方案中辛烷值損失的降幅比達到44.822%，且各主要變量最優值均處于合理取值范圍內。結果表明，本文所采用的數學模型與優化算法可以很好地對辛烷值損失問題進行預測與優化。