分段函數要求高 七種題型要記牢
■樊文聯
分段函數是在不同定義區間上具有不同的解析式,是一類重要的函數。在處理分段函數問題時,應對不同的區間進行分類討論,然后整合,這恰好是分類討論的一種體現。
題型1:求函數的值

點評
已知分段函數解析式求函數值的方法:①確定要求值的自變量屬于哪個區間;②代入該段的解析式求值。當出現f[f(x0)]的形式時,應從內到外依次求值。
題型2:求函數的值域
例2函數f(x)=的值域是()。
A.R B.[0,2]∪{3}
C.[0,+∞) D.[0,3]
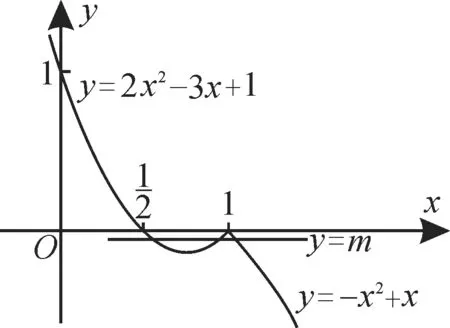
解:當0≤x≤1 時,0≤2x≤2,即0≤f(x)≤2;當1 點評 求分段函數的值域,就是求各段函數值域的并集。 例3已知分段函數f(x)=若f(a)=3,則實數a的值為_____。 解:根據題意可分段求解。①當a≤-2時,由f(a)=a+4=3,可得a=-1>-2,不合題意,舍去。②當-2 點評 已知分段函數的值求參數值的三個步驟:先對參數的取值范圍進行分類討論;然后代入不同的解析式,通過解方程求出參數的值;檢驗所求的值是否屬于所討論的區間。 例4已知分段函數f(x)=在區間 [-1,m]上的最大值是2,則實數m的取值范圍是_____。 解:當x≤0 時,f(x)=3-x-1 是減函數,所以3-x-1≤2,解得-1≤x≤0。當x>0時,f(x)=是增函數,所以≤2,解得0 點評 分段函數的求值或求取值范圍問題,要注意每段都應考慮是否滿足條件。 例5對于實數a和b,定義運算“*”:設函數f(x)=(2x-1)*x,且關于x的方程f(x)=m(m∈R)恰有三個互不相等的實根,則實數m的取值范圍是_____。 解:由新定義得函數f(x)=(2x-1)*作出分段函數f(x)的圖像,如圖1所示。 圖1 由函數的圖像與性質可知,當x=時,y=2x2-3x+1取得最小值為-。函數y=-x2+x在(1,+∞)上單調遞減,則y=-x2+x<0。因為y=f(x)=m(m∈R)恰有三個互不相等的實根,所以- 點評 本題是以新定義的形式來考查函數的圖像與性質的。題中要求方程的三個不相等的實根,只需求出對應函數圖像的三個交點即可。作圖、識圖、用圖是解答本題的關鍵。 點評 題中函數f(x)的定義域為[-1,0)∪(0,1]。-x與x的大小關系不確定,因此需要分類討論。 例7已知分段函數f(x)=是R 上的增函數,則實數a的取值范圍為()。 A.(1,+∞) B.(1,8) C.(4,8) D.[4,8) 點評 解決分段函數的單調性問題,要抓住對自變量所在區間的討論,在保證各段上同增(減)時,要注意上、下段間端點值的大小關系。 感悟與提高 若函數f(x)在閉區間[-1,2]上的圖像如圖2所示,則此函數的解析式為________。 提示:由圖可知,當-1≤x<0 時,f(x)=x+1;當0≤x≤2 時,f(x)=。所 以 函 數 圖2 題型3:求參數的值
題型4:求參數的取值范圍
題型5:新定義問題
題型6:不等式問題


題型7:單調性問題