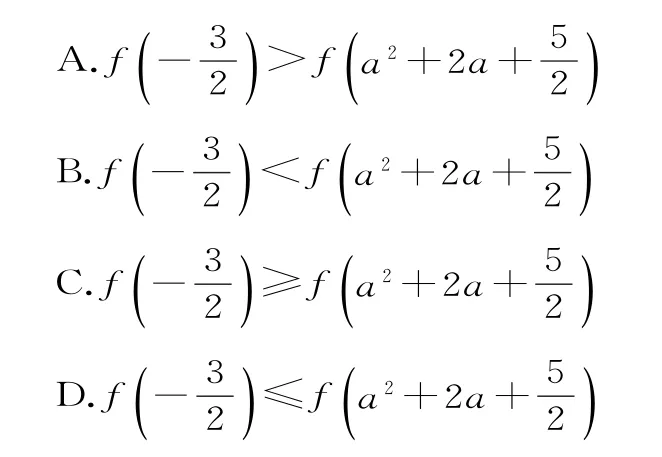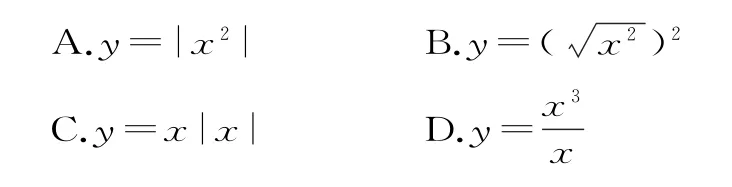函數的概念與性質核心考點綜合演練

■歐陽亮

一、選擇題

1.已知函數f(x)的定義域為(-1,3),則函數f(1-2x)的定義域是()。

3.已知函數f(x)對任意的x∈R,都有f(x+3)+f(x)=5,且f(0)=4,則f(2019)=()。

A.1 B.0

C.5 D.2

4.已知函數f(x)=ax3+bx++5,且f(6)=8,則f(-6)=()。

A.-8 B.3

C.-3 D.2

5.已知函數f(x)=x2+(k-2)x是[1,+∞)上的增函數,則k的取值范圍為()。

A.(-∞,0] B.[0,+∞)

C.(-∞,1] D.[1,+∞)

6.已知集合M={y|y=x-|x|,x∈R},N={y|y=,x∈R},則M∩N=()。

A.{0,1} B.{1}

C.{0} D.?

7.已知關于x的不等式x2-x+a-1≥0 在R 上恒成立,則實數a的取值范圍是()。

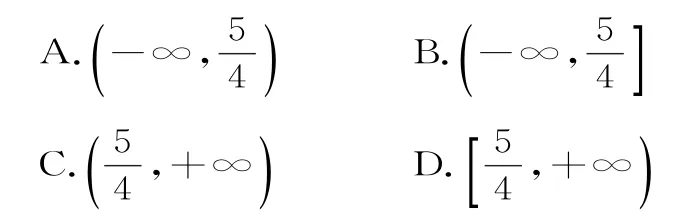
8.已知定義在R 上的函數f(x)滿足f(2-x)=f(x),且 當x∈[1,+∞)時,f(x)單調遞減。設a=f(2),b=,c=f(-1),則a,b,c的大小關系是()。

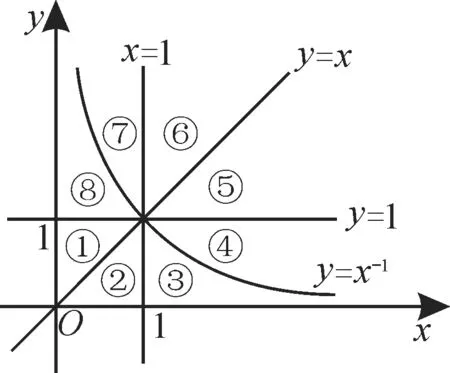
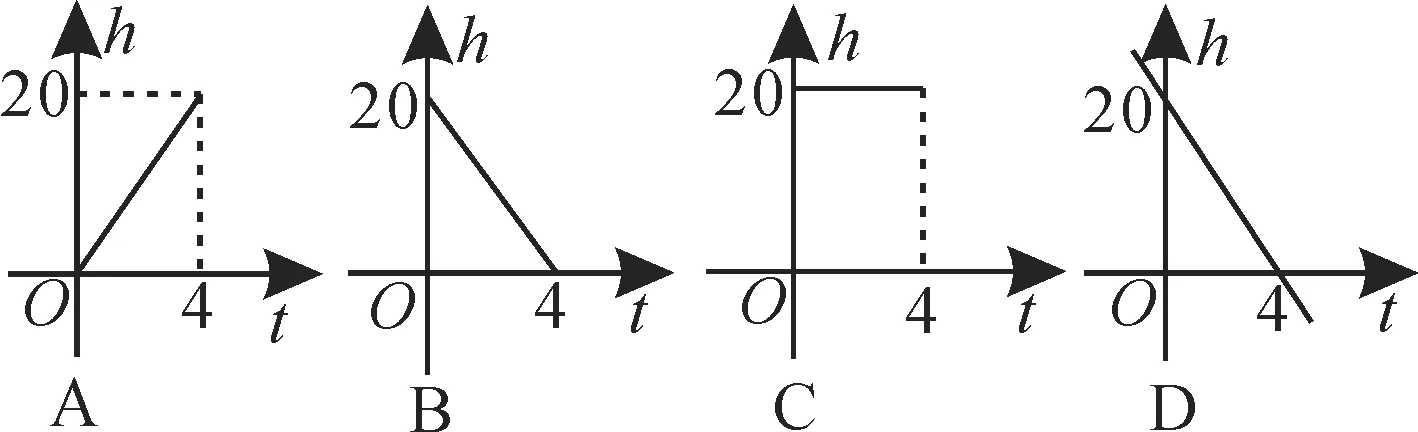
A.a

C.c

9.已知f(x)是偶函數,其定義域為(-∞,+∞),且在[0,+∞)上是減函數,則的大小關系是()。

10.冪函數y=x-1及直線y=x,y=1,x=1將平面直角坐標系的第一象限分成八個區域,分別標記為①②③④⑤⑥⑦⑧(如圖1所示),那么冪函數y=的圖像經過的區域對應的序號為()。

圖1

A.④⑦ B.④⑧

C.③⑧ D.①⑤

11.一根蠟燭長20cm,點燃后每小時燃燒5cm,燃燒時剩下的高度h(cm)與燃燒時間t(h)的函數關系用圖像表示為()。

12.國際上通常用恩格爾系數衡量一個國家和人民生活水平的狀況,它的計算公式為n=代表人均食品支出總額,y代表人均個人消費支出總額),且y=2x+475,各種類型的家庭標準如表1所示。

表1

張先生居住區2020年比2019年食品支出下降7.5%,張先生家在2020 年購買食品和2019年完全相同的狀況下,人均個人消費少支出75 元,則張先生家2020 年屬于()。

A.貧困 B.溫飽

C.小康 D.富裕

13.已知函數f(x)為R 上的單調函數,其圖像過點(0,-4)和點(2,2),則不等式|f(-x)+1|<3的解集為()。

A.[-4,2]

B.(0,2)

C.(-∞,-2]∪[0,+∞)

D.(-2,0)

14.已知定義在R 上的函數f(x)滿足f(x)=f(2-x),其圖像經過點(2,0),且對任意x1,x2∈(1,+∞),且x1≠x2,(x1-x2)·[f(x1)-f(x2)]>0恒成立,則不等式(x-1)f(x)≥0的解集為()。

A.(-∞,1]

B.[1,+∞)

C.(-∞,0]∪[1,2]

D.[0,1]∪[2,+∞)

15.已知f(x)是R 上最小正周期為2的周期函數,且當0≤x<2時,f(x)=x3-x,則函數y=f(x)的圖像在區間[0,6]上與x軸的交點個數為()。

A.6 B.7

C.8 D.9

16.函數y=f(x)為定義在R 上的奇函數,當x≥0時,f(x)單調遞增。若f(1)=1,則滿足-1≤f(x+2)≤1 的x取值范圍是()。

A.[-2,2] B.[-3,-1]

C.[-2,0] D.[1,3]

17.設f(x)是定義在R 上的增函數,且F(x)=f(x)-f(-x),那么F(x)必為()。

A.增函數且是奇函數

B.增函數且是偶函數

C.減函數且是奇函數

D.減函數且是偶函數

18.(多選題)下列函數中,與函數y=x2是同一函數的是()。

19.(多選題)函數f(x)的定義域為R,滿足:存在x1≠x2,使f(x1)≠f(x2);對任意的x,y,都有f(x+y)=f(x)·f(y)。則()。

A.f(0)=0 B.f(0)=1

C.f(x)<0 D.f(x)>0

二、填空題

20.已知af(x)+f(-x)=bx,其中a≠±1,則函數f(x)的解析式為_____。

21.某人以24.5萬元購買一輛高檔汽車,保險費、燃油費、停車費和其他一些雜費用每年要有3萬元,第一年不用維修,第二年的維修費用是1 萬元,以后每年的維修費用會比上一年遞增1萬元。設x為用車年數,則該車的年均費用的表達式為____。

22.已知函數f(x)是奇函數,函數g(x)與f(x)的圖像關于直線y=x+1 對稱,若g(1)=4,則f(-3)=_____。

23.設a∈R,若存在定義域為R 的函數f(x)滿足:①對任意x0∈R,f(x0)的值為x0或,②關于x的方程f(x)=a無實數解。則a的取值范圍是_____。

24.已知f(x)是定義在R 上的奇函數,f(x+1)是偶函數,則f(1)+f(2)+f(3)+f(4)=_____。

25.已知函數f(x)=2g(x)-x2為奇函數,若g(-1)=-1,則g(1)=____,f(1)=____。

26.將進貨單價為8元的商品按10元/個銷售時,每天可賣出100個,若此商品的銷售單價漲1 元,日銷售量就減少10 個,為了獲取最大利潤,此商品的銷售單價應定為____。

27.已知分段函數f(x)=在R 上為增函數,則實數b的取值范圍是____。

三、解答題

28.已知函數f(x)=ax2-2bx+5a+b為偶函數,其定義域為[2a+1,2-a]。

(1)求實數a,b的值。

(2)求函數f(x)的值域。

29.設函數f(x)為定義在R 上的奇函數,且對任意實數x,都有f(x+3)=-f(x),當x∈[0,3]時,f(x)=-x2+3x。

(1)求證:f(x)是周期函數。

(2)當x∈[3,6]時,求f(x)的解析式。

(3)求f(0)+f(1)+f(2)+… +f(2019)的值。

30.已知函數f(x)=是定義域為(-1,1)上的奇函數。

(1)確定f(x)的解析式。

(2)解不等式f(t-1)+f(t)<0。

31.定義在(-2,2)上的函數f(x)滿足:對任意的x,y∈(-2,2),都有f(x)+f(y)=,且 當x∈(-2,0)時,f(x)>0。

(1)判斷函數f(x)在(-2,2)上的奇偶性。

(2)判斷函數f(x)在(0,2)上的單調性。

(3)若f(1)=-1,解不等式:f(2x+1)<1。

32.某公司生產一種產品,每年投入固定成本0.5萬元,此外每生產100 件這種產品還需要增加投資0.25 萬元,經預測可知,市場對這種產品的年需求量為500 件,當出售的這種產品的數量為t(單位:百件)時,銷售所得的收入約為5t-(萬元)。

(1)若該公司的年產量為x(單位:百件),試把該公司生產并銷售這種產品所得的年利潤表示為年產量x的函數。

(2)當這種產品的年產量為多少時,當年所得利潤最大?

參考答案與提示

一、選擇題

1.提示:依題意可得-1<1-2x<3,解得x∈(-1,1)。應選A。

3.提示:由題意得f(x)=5-f(x+3),則f(x+3)=5-f(x+6),所以f(x)=5-[5-f(x+6)]=f(x+6),所以f(x)是周期為6 的周期函數。因為f(x+3)+f(x)=5,所以f(3)=5-f(0)=1,所以f(2019)=f(336×6+3)=f(3)=1。應選A。

11.提示:由題意得h=20-5t,0≤t≤4。結合圖像知,應選B。

12.提示:設2019年人均食品支出x元,則2020 年人均食品支出x(1-7.5%)=92.5%x(元),2020 年人均消費支出2×92.5%x+475。由題意可得2×92.5%x+475+75=2x+475,所以x=500。此時,n=≈0.3304=33.04%。由表知屬于富裕。應選D。

13.提示:函數f(x)是R 上的單調函數,且其圖像過點(0,-4),(2,2),可以判斷函數f(x)在區間(0,2)上的值域為(-4,2)。化簡|f(-x)+1|<3得-4

14.提示:由題意知f(x)關于直線x=1對稱,且f(2)=0,在(1,+∞)上單調遞增,所以f(x)在(-∞,1)上單調遞減,且f(0)=0。畫出f(x)的簡圖可幫助求解(圖略)。當x≥1 時,f(x)≥0,即x∈[2,+∞);當x≤1時,f(x)≤0,即x∈[0,1]。綜上可得,x∈[0,1]∪[2,+∞)。應選D。

15.提示:由f(x)是最小正周期為2 的周期函數,且當0≤x<2 時,f(x)=x3-x=x(x-1)(x+1),可得當0≤x<2 時,f(x)=0有兩個根,即x1=0,x2=1。由周期函數的性質知,當2≤x<4 時,f(x)=0有兩個根,即x3=2,x4=3,當4≤x<6 時,f(x)=0有兩個根,即x5=4,x6=5,但x7=6也是f(x)=0的根,所以函數f(x)的圖像在區間[0,6]上與x軸交點的個數為7。應選B。

16.提示:函數y=f(x)為定義在R 上的奇函數,由f(1)=1,可知f(-1)=-1。當x≥0時,函數f(x)單調遞增,由y=f(x)為定義在R 上的奇函數,可得y=f(x)在R 上單調遞增。由-1=f(-1)≤f(x+2)≤f(1)=1,可得-1≤x+2≤1,即-3≤x≤-1。應選B。

17.提示:由F(-x)=f(-x)-f(x)=-F(x),可得F(x)為定義在R 上的奇函數。設x2>x1,則F(x2)-F(x1)=f(x2)-f(-x2)-f(x1)+f(-x1)。由x2>x1,可得-x2<-x1。由f(x)為定義在R 的增函數,可得f(x2)>f(x1),f(-x1)>f(-x2),所以F(x2)-F(x1)=[f(x2)-f(x1)]+[f(-x1)-f(-x2)]>0,所以F(x)為定義在R 上的增函數。綜上所述,F(x)必為增函數且為奇函數。應選A。

18.提示:對于A,B,顯然與函數y=x2是同一函數。對于C,當x<0 時,y=x|x|=-x2,與函數y=x2不是同一函數。對于D,函數y=的定義域為(-∞,0)∪(0,+∞),與函數y=x2不是同一函數。應選A,B。

19.提示:令y=0,則f(x)=f(x)·f(0)。若f(0)=0,對任意的x1≠x2,f(x1)=f(x2)=0,不符合題意,故f(x)>0,則f(0)=1。令y=x,則f(2x)=f2(x)≥0。因為f(x)≠0,所以f(2x)>0,f(x)>0。應選B,D。

二、填空題

23.提示:由函數的定義知,一個自變量只能對應一個函數值,可得x0=,解得x0=0或x0=1,所以f(0)=0或f(1)=1。因為關于x的方程f(x)=a無實數解,所以f(a)=a2≠a,可得a≠0 且a≠1。故a∈(-∞,0)∪(0,1)∪(1,+∞)。

24.提示:由f(x+1)是偶函數得f(-x+1)=f(x+1)。由f(x)是定義在R上的奇函數,可得f(-x+1)=-f(x-1),即-f(x-1)=f(x+1),所以f(x+2)=-f(x),即f(x)+f(x+2)=0。所以f(1)+f(3)=0,f(2)+f(4)=0,因此f(1)+f(2)+f(3)+f(4)=0。

25.提示:因為函數f(x)=2g(x)-x2為奇函數,且f(1)=2g(1)-1,f(-1)=2g(-1)-1,所以f(1)+f(-1)=2g(1)+2g(-1)-2=0,所以g(1)=2。所以f(1)=2g(1)-1=2×2-1=3。

26.提示:設銷售單價應漲x元,則實際銷售單價為(10+x)元,此時日銷售量為(100-10x)個,每個商品的利潤為(10+x)-8=2+x(元),可得總利潤y=(2+x)·(100-10x)=-10x2+80x+200=-10(x-4)2+360(0

27.提示:要使此函數為R 上的增函數,需滿足函數g(x)=(2b-1)x+b-1在(0,+∞)上是增函數,函數h(x)=-x2+(2-b)x在(-∞,0]上是增函數,且滿足h(0)≤g(0)。根據一次函數和二次函數的單調性可得解得1≤b≤2,即實數b的取值范圍是[1,2]。

三、解答題

28.提示:(1)由偶函數f(x)的定義域為[2a+1,2-a],可得2a+1+2-a=0,即a=-3。由函數f(x)為二次函數,對稱軸為y軸,可得b=0。

(2)由(1)可得f(x)=-3x2-15,x∈[-5,5]。由二次函數的圖像與性質得此函數的值域為[-90,-15]。

29.提示:(1)由f(x+3)=-f(x),可得f(x+6)=-f(x+3)=f(x),所以f(x)是周期為6的周期函數。

(2)當x∈[-3,0]時,-x∈[0,3],可得f(-x)=-(-x)2+3(-x)=-x2-3x。由f(x)是奇函數,可得當x∈[-3,0]時,f(x)=-f(-x)=x2+3x。當x∈[3,6]時,x-6∈[-3,0],則f(x-6)=(x-6)2+3(x-6)=x2-9x+18。由f(x)是周期為6 的周期函數,可得當x∈[3,6]時,f(x)=f(x-6)=x2-9x+18。

(3)由f(0)=0,f(1)=2,f(2)=2,f(3)=0,f(4)=-2,f(5)=-2,可得f(0)+f(1)+f(2)+f(3)+f(4)+f(5)=0。因為f(x)是周期為6 的周期函數,且2020=6×336+4,所以f(0)+f(1)+f(2)+… +f(2019)=f(0)+f(1)+f(2)+f(3)=4。

31.提示:令x=y=0,可得f(0)=0,再令y=-x,可得f(x)+f(-x)=f(0)=0,所以f(x)=-f(-x),可知函數f(x)在(-2,2)上為奇函數。

(3)由(2)可得函數f(x)在(0,2)上單調遞減。由f(x)為奇函數,當x∈(-2,0)時,f(x)>0,可得函數f(x)在(-2,2)上單調遞減。由f(1)=-1,可得f(-1)=1。由f(2x+1)<1,可得f(2x+1)

32.提示:(1)設利潤為y萬元,R(t)=

因為生產一種產品的固定成本為0.5萬元,每生產100件,需增加投入0.25萬元,所以當產量為x百件時,成本為0.5+0.25x。因為市場對此產品的年需求量為500 件,所以當x≤5 時,產品能售出x百件,當x>5時,只能售出500 件。故利潤函數y=代入整理得

(2)當05時,y<12-0.25×5=10.75(萬元)。故當年產量為475件時,當年所得利潤最大。