人口規模、創新投入與全要素生產率
——基于京津冀13個地級市的實證分析

曾雪婷，向 華，童玉芬

(首都經濟貿易大學 a.人口經濟研究所；b.勞動經濟學院 北京 100070)

一、問題提出

一直以來，人們都將人口城鎮化率作為城市化發展水平的評判標準。相比農村，城市轄區內較低的勞動力和運輸成本、生產要素獲取的便利性及生產加工過程中的專業化分工優勢更有利于企業發展、技術創新和實現國家經濟增長[1]。依據經濟增長理論，城市全要素生產率指數比傳統的國內生產總值(GDP)更能準確衡量城市的發展水平。

面對國家創新型經濟發展的需要，各級政府逐步放松落戶政策，中國城鎮建設得到了快速發展。1978—2019年，中國城市化水平由17.92%提高到60.60%，城鎮人口規模達8.48億人[2]。據國家統計局數據顯示，2019年中國GDP為99.1萬億元，是1978年GDP(3 678.7億元)的296.4倍。當下，中國GDP總量排名僅次于美國，位居世界第二。然而，中國經濟所取得的巨大進步，不僅是人力、資本(政府支持和企業投資)積累的作用，還是城市技術進步和全要素生產率提高的結果。雖然目前中國城鎮化率已超過60%，GDP排名位居世界第二，但是與歐美發達國家城鎮化率(80%)和人均GDP水平相比還存在很大差距。

隨著國家經濟水平的不斷發展，國內生態環境也遭受了一定的破壞，陸續出現城市資源承載力下降、城市經濟發展亟須轉型等現實問題，尤其是對超大型城市而言，上述問題尤為突出。針對人口規模擴大對城市生產率方面的探討，已有研究在影響機制、評價方法和研究結論方面均存在一定的分歧。許多學者認為，城市人口規模會隨著產業集聚而逐漸擴大，人口規模擴張雖然在一定程度增加了城市人力資本的積累[2-3]，但同時也給城市帶來了嚴重的環境問題[4-6]。針對此現象，政府也出臺了相應的人口疏解、限制人口遷移的政策措施。城市人口規模擴大會促使城市向周邊外延，擴大城市規模，在城市集聚效應和資本積累的基礎上，提高城市勞動生產率(每單位勞動的產出)。從經濟增長理論出發，人口和資本要素只有合理配置時，才會帶來遞增的邊際效應。換言之，城市的經濟增長不僅需要人口積累，政府和企業的投資(尤其是創新投資)也十分重要。

為探究人口規模、創新投資與城市全要素生產率發展水平的相關關系及影響機制，本文將以京津冀城市群(包含典型特大城市)2009—2018年城市投入產出數據為研究對象，在測算城市生產率的基礎上，把握城市發展水平及空間差異。進一步構建動態面板回歸模型，分析人口規模、創新投入對城市全要素生產率及其分解指數的作用機理，以期為京津冀協同發展中心進一步制定城市發展政策措施提供參考。

與現有研究相比，本文存在以下創新點：(1)使用京津冀地區13個城市市轄區數據，有別于其他學者使用省級面板數據的研究。(2)以往許多學者主要以GDP來刻畫城市產出，鑒于GDP計量水平的局限性，本文參考王德利和王巖(2016)[7]的做法，除GDP以外，還將政府財政收入也作為另一個產出變量，以增加評價的準確性。(3)本文參考劉斯敖(2020)[8]的做法，選取SBM-ML指數法來測算城市全要素生產率，基于松弛測度(slacks-bosed measure，SBM)模型在分析中考慮了決策單元投入要素投影至生產前沿面的過程中非徑向改進水平，優于常規CCR模型只考慮徑向等比改進，以更真實全面地反映城市全要素生產率。(4)已有文獻只關注人口規模(城市市轄區總人口)或創新投入(政府或企業的創新投入)對城市生產率的影響，忽略了二者之間的協同作用，本文將城市人口規模(市轄區總人口規模、高層次人才人口規模)、創新投入(政府創新投入、企業創新投入)共同納入評價模型中，以檢驗其與城市全要素生產率的相關關系。(5)分別對全要素生產率及其分解指數構建回歸方程，以區分人口規模、創新投入對城市生產率影響的側重點及差異。

二、研究方法和數據說明

(一)研究方法

目前，關于全要素生產率的研究，大多數學者主要選取SBM-DDF模型和曼奎斯特-龍伯格(Malmquist-Luenberger，ML)生產率指數法來測算分析城市全要素生產率和全要素生產率，這一方法有效避免了非最優決策單元在生產前沿面上徑向改進模型的不足，同時還考慮了非徑向改進的松弛變量。本文在已有研究的基礎上，運用SBM-DDF-ML法對京津冀地區13個城市全要素生產率進行測算，并將其分解為技術進步和綜合技術效率[9]。

1. SBM方向距離函數

方向距離函數(directional distance function，DDF)模型是對徑向數據包絡分析(DEA)模型的一般化表達[10]。在DDF模型中決策者可自定義被評價決策單元向生產前沿面的投影的方向，有效地將主管偏好與DEA模型相結合。DDF通過設定特定方向將生產率與環境污染納入同一個框架中，使期望產出和非期望產出沿著某一方向產生同等程度的改進，因其不需要考慮產出的價格因素而在生活中得到廣泛應用[11]。但是單一的DDF因其徑向、角度的度量方法忽略了投入和期望產出的松弛問題。在徑向DEA模型中，對無效率程度的測量只包含了所有投入(產出)等比縮減(增加)的程度；而對無效決策單元來說，其當前狀態與強有效目標值之間的差距除了等比例改進部分之外，還包括松弛改進部分。有學者指出，沒有考慮松弛變量的生產率取值不準確，因此，為更有效地對決策單元效率做出評價，需要選擇非徑向非角度(non-oriented)的DEA模型[12]。

為解決徑向和角度DEA模型的不足，SBM模型被提出。該模型將松弛變量直接納入目標函數，剔除了變量松弛造成的非效率因素，解決了考慮非期望產出在內的全要素生產率評價問題。同時SBM模型無量綱性和非徑向特點，能夠有效避免量綱不同和角度選擇差異給生產率評價帶來的偏差。根據假設，有K個需要被評價的決策單元(DMUj，j=1，2，3，...，k)，每個DMU包含投入、期望產出和非期望產出三類指標，其中有投入指標m種(i=1，2，...，m)，n種期望產出和h種非期望產出，x∈Rm，y∈Rn，u∈Rk，定義矩陣如下：X=[x1，x2，...，xk]∈Rmk，Y=[y1，y2，...，yk]∈Rnk，U=[u1，u2，...，uk]∈Rkk，將非導向SBM規劃式定義如下：

(1)

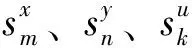
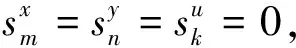
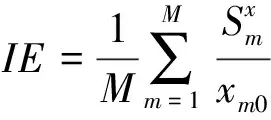
(2)

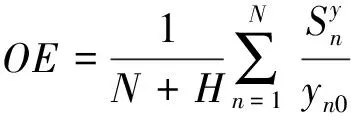
(3)

2. DEA-Malmquist指數

本文將考慮非期望產出的SBM-DDF模型與ML生產率指數相結合的方式來測度京津冀地區城市全要素生產率，從t時期到t+1時期的ML指數為：

(4)

則ML指數可進一步分解為技術進步(Tech)和技術效率(Effch)改進指數：

(5)

(6)

(7)

Tech指數測度技術前沿的進步速度，Effch指數反映技術落后者向前沿技術者的追趕速度。TFP、Tech、Effch指數數值大于(小于)1，分別表示TFP增加(減少)、技術進步(退步)和技術效率提高(下降)。

TFP指數在求解過程中需要對四個方向性距離函數進行計算，分別是t期技術和t期投入產出值的DDF；t+1期技術和t+1期投入產出值的DDF；t期技術與t+1期投入產出值的DDF；t+1期技術與t期投入產出值的DDF。

(二)數據說明

1.指標選取及度量

全要素生產率是指一個經濟系統或企業使用所有要素的效率，通常用于衡量技術進步和效率水平。根據已有研究，綜合考慮指標的獲取性、準確性、真實性等原則，本文將參考孟望生和邵芳琴(2020)[14]的指標選取辦法，將城市地區生產總產值(億元)、城鎮地區財政總收入(億元)作為產出指標，將城鎮年末勞動力就業總人數(萬人)、城鎮私營企業和個體人員數(萬人)、城鎮社會固定資產投資(億元)、城市建成區面積(平方公里)作為投入指標。與以往研究不同的是，本文依據索羅余值方程，除了將勞動、資本作為要素投入外，還將土地投入(城市建成區面積)也納入模型[7]。具體指標解釋說明如表1所示。

表1 指標及度量

2.數據來源與處理

本文所使用的投入產出數據均來源于2010—2019年國家統計局《中國城市統計數據庫》，部分指標依據論文分析需要進行了單位換算處理。此外，對于個別城市少數年份的缺失數據，通過線性插值法進行了填補[2]。

三、實證分析與結果討論

(一) 全要素生產率及其分解

基于測算結果，將全要素生產率指數分解為技術進步指數和綜合技術效率指數，并分別從時間、空間兩個維度對京津冀地區13個城市的全要素生產率及分解指數進行對比分析，以明確不同城市在不同時間段的發展水平及時空差異。

1.全要素生產率指數時空差異分析

2009—2018年，京津冀地區城市全要素生產率指數在均值為1.071，城市群整體發展水平上升7.1%。其中，北京、邯鄲、邢臺、廊坊、承德、衡水的全要素生產率均值上升幅度大于京津冀地區城市全要素生產率變動均值，表明近10年上述城市發展較好；天津、石家莊、保定、滄州、秦皇島的全要素生產率變動均值低于京津冀地區城市全要素生產率變動均值，說明上述城市處于低速發展階段；唐山和張家口的全要素生產率指數低于1，表明其城市不僅沒有取得進步，相比其他城市而言，反而出現倒退現象(見表2)。

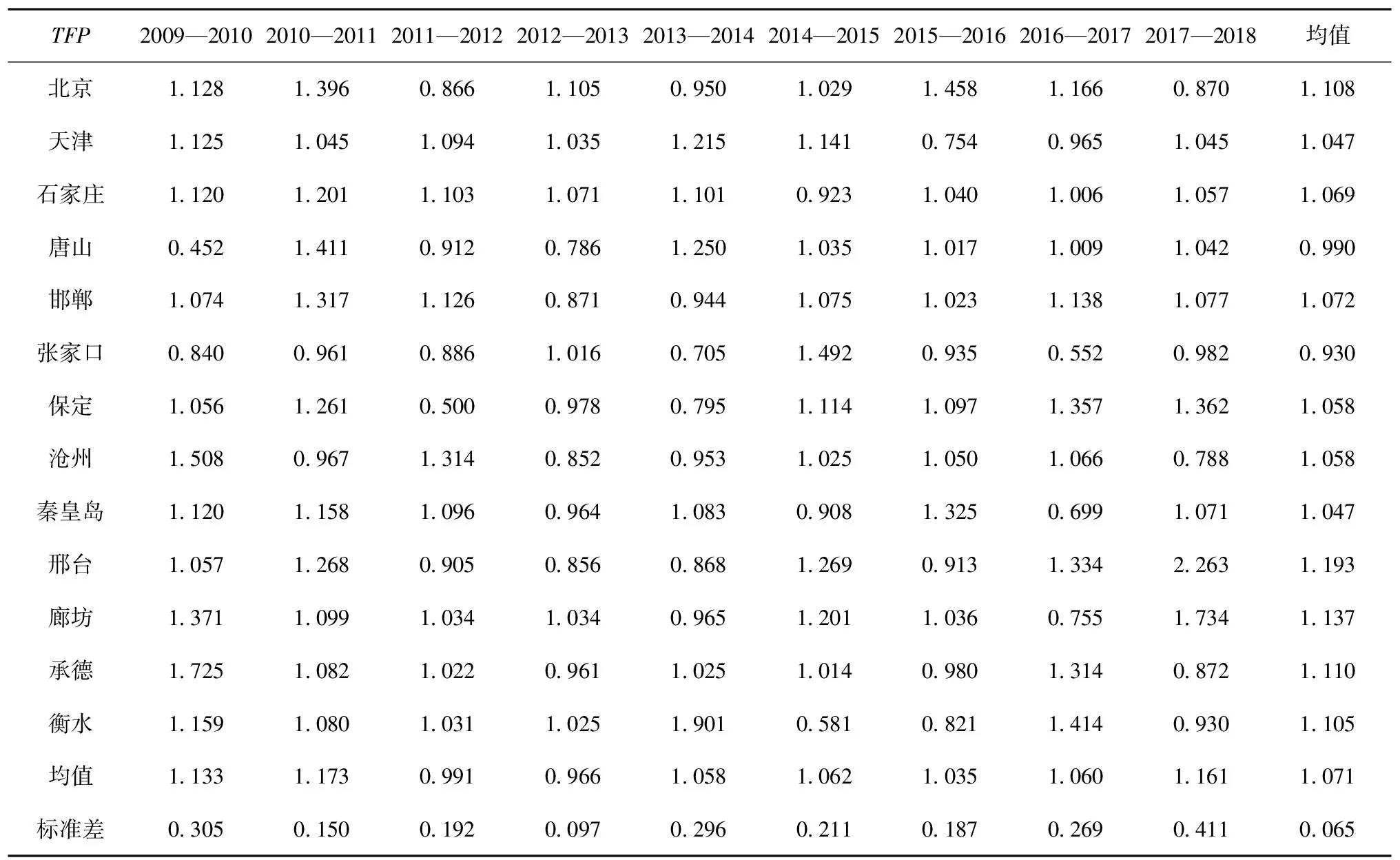
表2 2009—2018年京津冀地區城市全要素生產率指數

從時間變動趨勢來看，2009—2018年北京、天津、石家莊等8個城市的全要素生產率指數在小范圍內波動，表明上述城市發展平穩，受外界影響因素較小。保定、唐山、衡水、邢臺、張家口5個城市的全要素生產率指數在不同時間段內波動較大，表明上述城市發展受外界影響相對較高。進一步分析發現，2009—2010年唐山全要素生產率指數異常，為0.452，主要受綜合技術效率指數拖累(0.435)，同期技術進步指數1.039；衡水全要素生產率指數在2013—2014年取值異常，為1.901，受綜合技術效率指數拉動作用明顯(1.825)，同期技術進步指數1.042；2017—2018年邢臺全要素生產率指數異常高，取值1.198，受技術進步指數(1.070)和綜合技術效率指數(1.128)雙重作用進步的影響；2011—2012年保定全要素生產率指數取值異常，僅0.500，受綜合技術效率拖累所致，綜合技術效率取值0.470，同期技術進步指數取值1.063；2014—2017年，張家口全要素生產率指數出現直線下滑趨勢，由1.492降至0.552，降幅達63%，受綜合技術效率下滑影響顯著，其綜合技術效率指數由2.080降至0.554，降幅達73.4%，同期技術進步上漲41.4%(見表3和表4)。上述分析表明，京津冀地區各城市技術穩步發展，波動幅度不明顯，綜合技術效率水平在時間、空間兩個維度存在較明顯的差異，受地區和時間因素影響較大。

2.綜合技術效率指數時空差異分析

由表3可知，2009—2018年，京津冀地區城市綜合技術效率指數均值為1.036，增幅為3.6%，略低于全要素生產率指數的增幅，再次表明城市全要素生產率指數的增加受綜合技術效率和技術進步的雙重影響。北京、天津、石家莊、邯鄲、滄州、承德的綜合技術效率指數均值呈上升趨勢，但上升幅度低于京津冀地區平均水平。保定、邢臺、廊坊的綜合技術效率指數均值上升顯著，大于京津冀地區平均上升水平。這主要是因為，相比京津冀地區其他城市而言，上述三個城市基礎水平相對落后，隨著社會整體進步和北京引領作用的顯現以及自身經濟發展需要，保定、邢臺和廊坊在城市綜合管理水平和資源利用效率方面有較大改善；唐山、張家口和秦皇島在綜合技術效率指數方面呈倒退趨勢，綜合技術指數變動均值小于1。上述現象主要受兩方面的影響，一方面是地區和氣候限制，使得資源利用率相對較低，另一方面則是綜合技術效率進步較小，相比京津冀地區其他城市而言呈現出落后的態勢。

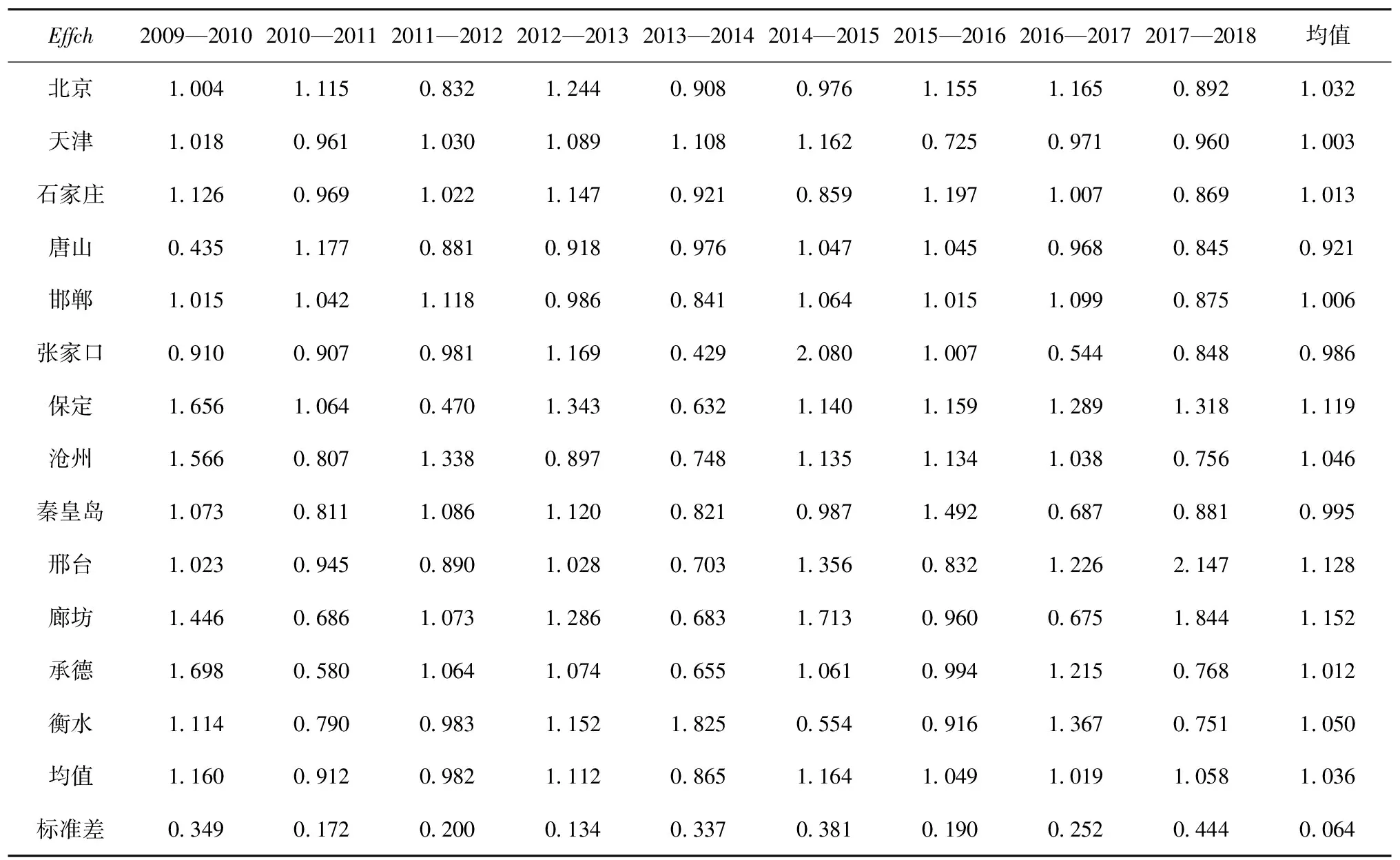
表3 2009—2018年京津冀地區城市綜合技術效率指數

從時間變動趨勢來看，2009—2018年北京、天津、石家莊等7個城市的綜合技術效率指數在小范圍內波動，表明上述城市在發展過程中重視資源利用效率和管理水平的提升，讓城市在現有水平上穩定運行。保定、廊坊、衡水、邢臺、張家口、唐山6個城市的綜合技術效率指數在不同時間段內波動較大，整體情況與全要素生產率變動態勢相一致，呈現高度相關關系，也再次印證城市全要素生產率指數的提高對綜合技術效率依賴較大。上述分析表明，京津冀地區各城市在制定發展規劃過程中，不應只強調科學技術對城市發展的貢獻，在技術取得進步的同時，城市管理水平也應該得到同步提升，使技術水平和管理能力相協調。

3.技術進步指數時空差異分析

2009—2018年，京津冀地區城市技術進步指數均值為1.062，上升6.2%。其中，北京、石家莊、唐山、邯鄲、秦皇島、邢臺、廊坊、承德、衡水9個城市的技術進步指數均值上升幅度大于等于京津冀地區城市技術進步指數變動均值，表明上述城市整體技術水平取得較好發展，在拉動京津冀地區城市整體技術水平上起著良好引領帶動作用；天津、張家口、保定、滄州4個城市的技術進步指數均值增幅低于京津冀地區城市技術進步指數平均水平，尤其是保定的技術進步指數均值小于1，表明相比其他城市而言，保定在科技創新方面明顯滯后。對比綜合技術效率發現，保定在技術效率提升方面也不穩定。上述城市技術進步指數表明，城市全要素生產率的提高，較大程度依賴于技術進步。進一步分析發現，保定連接北京和石家莊，雖然承擔部分北京的疏解產業，但是大部分仍然是技術含量較低的服務業和輕工業，對技術要求較低。在環境管制的限制下，大部分輕工業在冬季會經常被關停，這嚴重影響企業長期發展和技術創新的信心(見表4)。

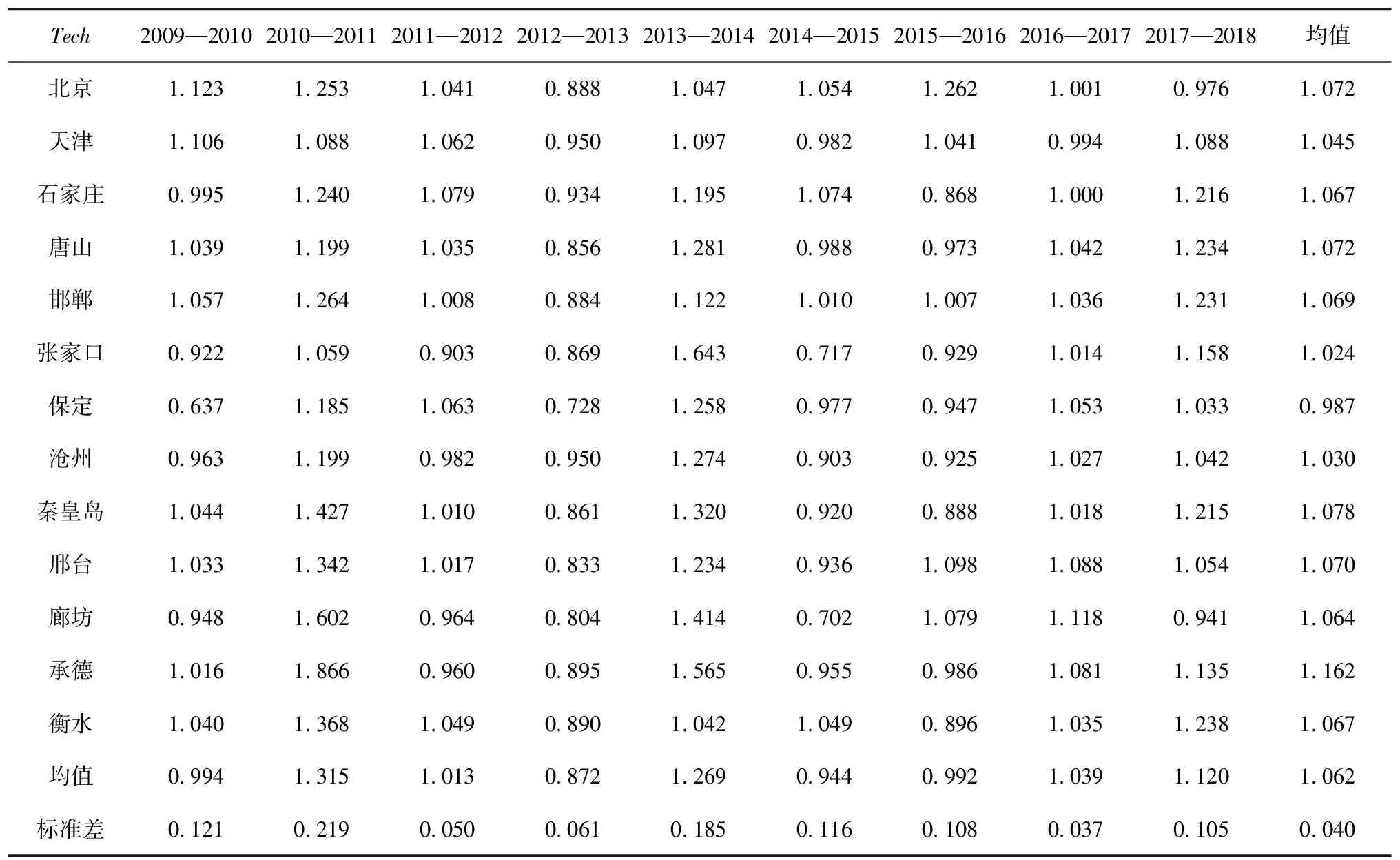
表4 2009—2018年京津冀地區城市技術進步指數

從時間變動趨勢來看，2009—2018年京津冀的13個城市，技術進步指數變動趨勢基本保持一致，只有承德、廊坊和保定3個城市在考察初期(2009—2015年)技術進步變動較大，分別在2010—2011年、2013—2014年兩個時期達到極值，其余時期均在小范圍內波動。分析表明京津冀地區13個城市在過去十年，尤其是最近四五年，戰略目標逐步向城市技術進步傾斜，在提升管理水平的同時也兼顧技術水平的發展。分析發現，技術進步指數在時間趨勢上基本穩定，在空間上的差異也不明顯，表明京津冀地區協同發展政策的實施，有效提高了先進技術的傳播速度和推廣范圍，讓以北京為核心的京津冀地區其他城市在先進技術的推動下，實現城市經濟、社會的共同發展。

(二) 2009—2018年城市無效率值的來源分解

分析京津冀地區13個城市生產投入冗余和產出不足取值可發現，北京和天津2個城市在所有投入和產出要素上均沒有冗余或不足，表明北京、天津相比河北11個城市，具有明顯的效率優勢，這也符合現實情況和客觀認知規律，表明數據選取和方法計算具有良好的穩健性(見表5)。

從城市勞動力投入——城鎮單位年末就業人員來看，2018年京津冀地區該要素投入冗余均值為2.35萬人，冗余標準差為3.51，表明在勞動力就業投入要素上，不同城市之間差異顯著，但是整體冗余程度不嚴重。其中石家莊、邯鄲、張家口、承德4個城市勞動力就業人員冗余值高于京津冀地區平均水平，表明上述城市在生產發展過程中，勞動力利用率較低，城市距離非參數的最優生產前沿面較遠。

從固定資產投資冗余來看，2018年京津冀地區在該要素投入冗余均值為170.92億元，冗余標準差為276.50，表明在固定資產投入要素上，京津冀地區對資本投入的利用率較低，不同城市之間差異顯著，且整體冗余水平很高，唐山、邯鄲和張家口3個城市冗余異常高，分別為489.89億元、913.39億元和211.51億元。單獨對唐山進行要素投入和產出分析發現，唐山的資本投入與勞動力投入嚴重不匹配，表現出資本過多而勞動力不足的現象，以至于政府花了錢，但是產出效益較低的情況。

從建成區面積冗余值來看，2018年京津冀地區在該要素投入冗余均值為31.17平方公里，冗余標準差為32.87，表明在城市建成區面積(土地)投入要素上，京津冀地區對城市土地投入的利用率較低，且不同城市之間差異顯著(見表5)。

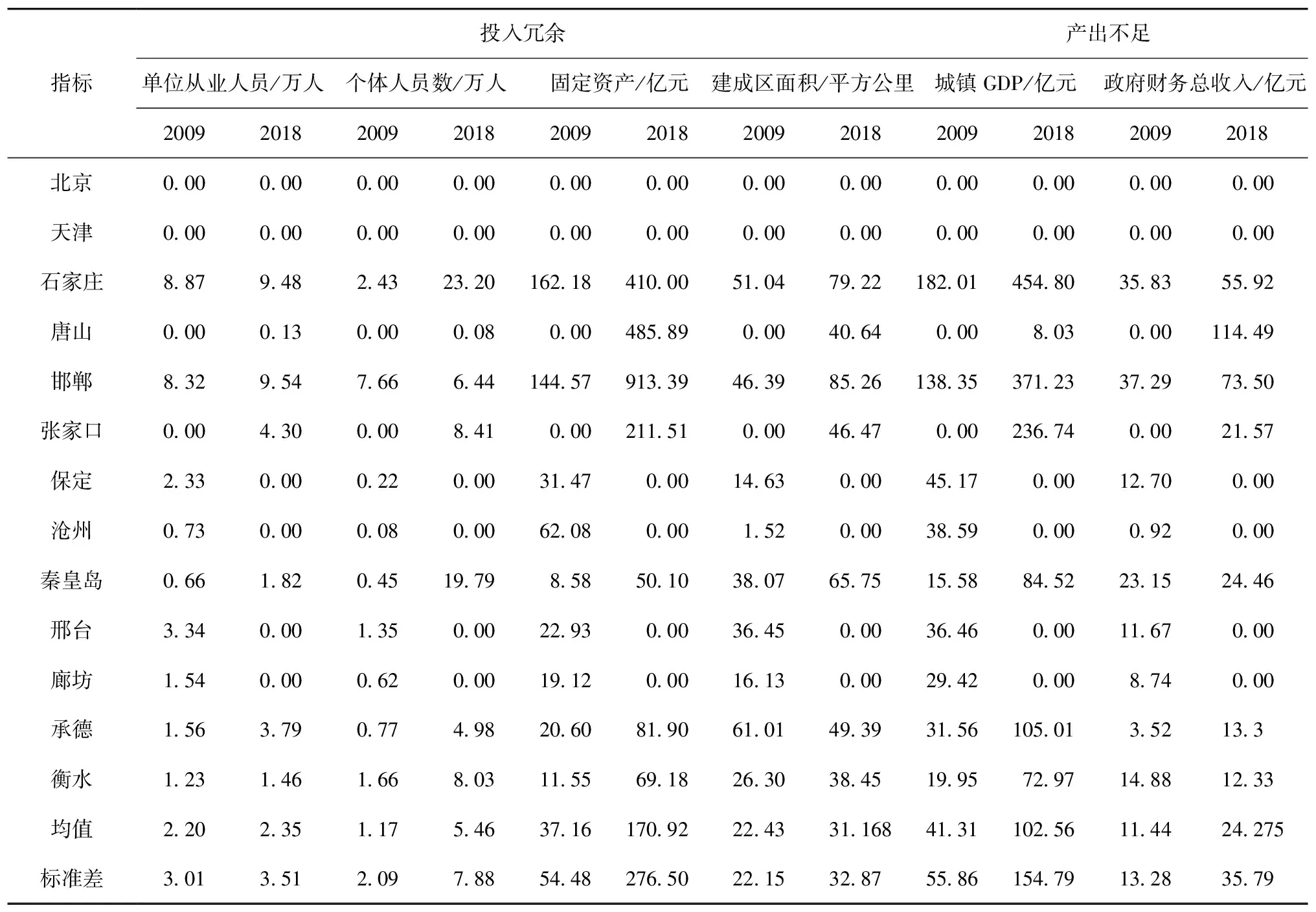
表5 2009年和2018年京津冀地區城市完全投入冗余和產出不足

綜合分析京津冀地區各城市要素投入冗余發現，大部分城市在投入要素綜合利用率上處于較低水平。從經濟學生產周期理論分析，石家莊、唐山、邯鄲、秦皇島等城市的發展水平已進入生產曲線的第三階段。在當前技術限制水平下，投入要素利用率低，如果不提高技術進步，持續增加投入會擴大邊際報酬遞減水平，降低城市全要素生產率。

對比2009年和2018年京津冀地區13個城市各投入要素冗余和產出要素不足的均值和標準差發現，2009年城市之間各要素平均無效率程度較低，尤其是勞動力投入，冗余值很小，表明在2009年京津冀地區城市發展對城鎮勞動力利用效率較高。對比2018年分析發現，京津冀地區在城市發展建設過程中，對社會固定資產投資的利用效率較低，且不同城市之間利用率程度差異顯著。2018年京津冀地區生產總值產出不足均值較大，取值為102.56億元，不同城市之間地區生產總值產出不足水平存在明顯差異(標準差取值154.79)。

四、人口規模、創新投入對城市全要素生產率的實證分析

(一)模型設定與變量說明

1.模型設定

為探究人口規模、城市創新投入對城市全要素生產率的影響，本文構建如下計量回歸分析模型：

TFPi，t=β0+β1lnPeoScalei，t+β2(lnPeoScalei，t)2+β3lnGovCreIi，t+β4(lnGovCreIi，t)2+

β5lnComCreIi，t+β6(lnComCreIi，t)2+β7TFPi，t-1+αXi，t+ui+γt+εi，t

(8)

其中，i代表城市，t表示年份，TFPi，t為被解釋變量，表示i城市在t時期的全要素生產率取值。核心解釋變量包括：lnPeoScalei，t表示當期城鎮人口規模(取對數處理)、(lnPeoScalei，t)2表示當期人口規模取對數后的平方項，lnGovCreIi，t表示當期城市政府創新資金投入(取對數處理)，(lnGovCreIi，t)2表示政府當期創新資金投入取對數后的平方項，lnComCreIi，t和(lnComCreIi，t)2分別表示當期企業創新資金投入額度(取對數處理)及其平方項，TFPi，t-1為前一期城鎮全要素生產率取值，Xi，t為所有控制變量集合，包括外商直接投資(lnFDI)、城市交通建設水平(lnTransP)；ui為個體固定效應，用于控制不同城市間影響機制的差異；γt為時間固定效應，主要用來剔除時間趨勢項對回歸結果的影響；εi，t為隨機擾動項，主要是指未包含在模型中的解釋變量和其他隨機因素對被解釋變量產生的總影響集合。

為進一步探究核心解釋變量對城市全要素生產率的影響機制，本文在全要素生產率指數分解的基礎上，分別構建回歸模型，以進一步分析核心解釋變量對城市技術進步和技術效率的影響機制。具體形式如下：

Techi，t=β0+β1lnPeoScalei，t+β2(lnPeoScalei，t)2+β3lnGovCreIi，t+β4(lnGovCreIi，t)2+

β5lnComCreIi，t+β6(lnComCreIi，t)2+β7Techi，t-1+αXi，t+ui+γt+εi，t

(9)

Effchi，t=β0+β1lnPeoScalei，t+β2(lnPeoScalei，t)2+β3lnGovCreIi，t+β4(lnGovCreIi，t)2+

β5lnComCreIi，t+β6(lnComCreIi，t)2+β7Effchi，t-1+αXi，t+ui+γt+εi，t

(10)

2.變量

在進行實證分析之前，首先對回歸模型(8)—模型(10)中的變量進行說明，并進一步對各變量做描述性統計分析，具體指標見表6和表7。其中企業創新投資規模，由于統計數據中沒有相應直接統計指標對其進行度量，因此本文選取城市專利申請數量來表示企業創新投資，各城市專利申請數量用三種專利受理數量表示，其中河北省只有省級層面數據，各市專利受理數量=(各市市轄區GDP/河北省市轄區GDP)×河北省專利受理總量。用此指標來度量企業創新投資，比直接利用企業資金投資總額度量更加準確，因為企業創新投入通常包含科技研發之外的其他支出。

表6 變量說明

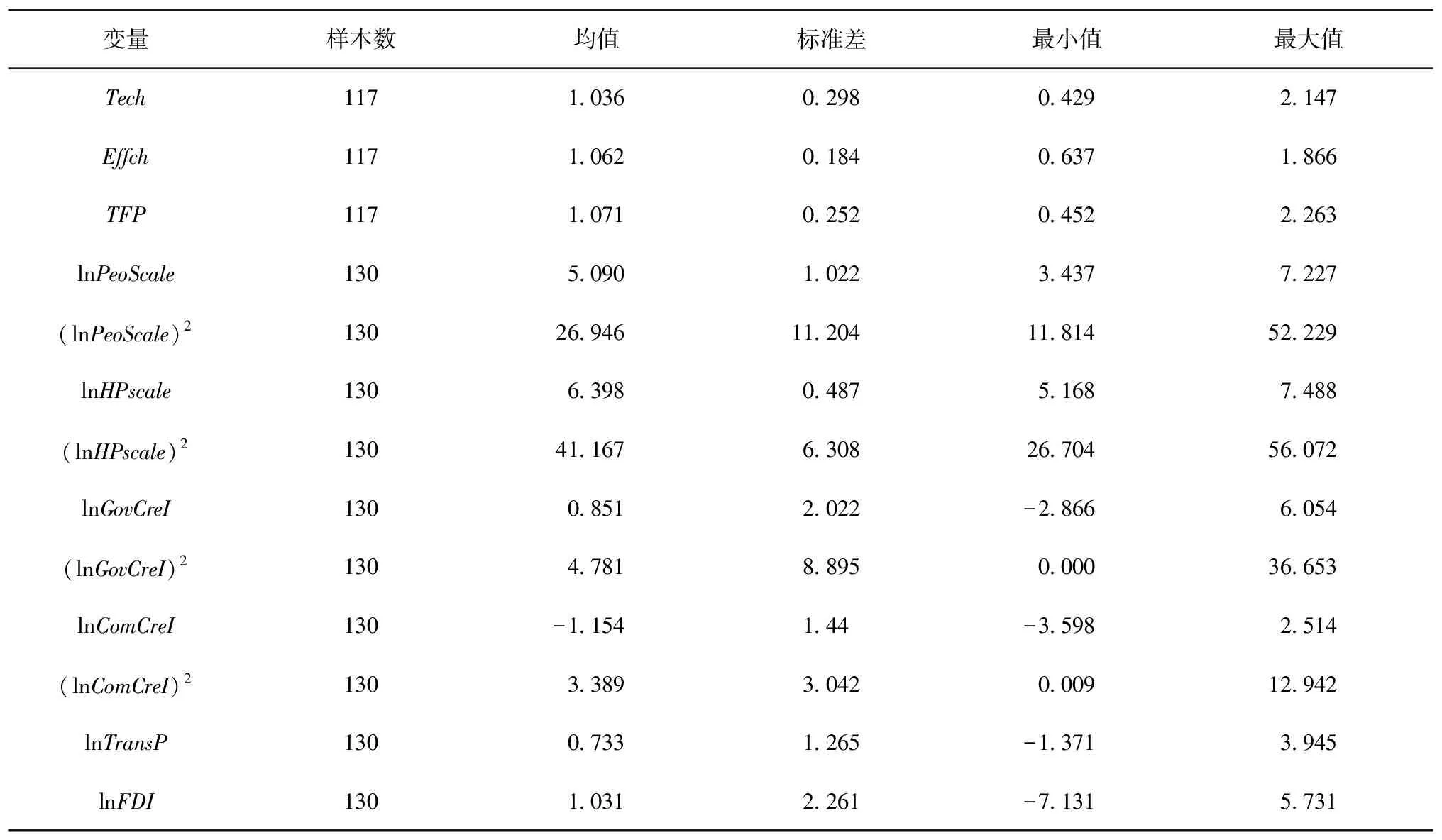
表7 變量描述性統計

(二)估計方法及其原理

在動態面板數據模型的解釋變量中，加入被解釋變量的滯后項。尼克爾(Nickel，1981)用數學推導證明了被解釋變量的滯后一期數據與擾動項的協方差不為0，即cov(CHIi，t-1，εit)≠0，則出現自相關和內生性問題，且變量間亦可能存在聯立性[15]。安德森和蕭(Anderson & Hsiao，1982)進一步證明使用固定效應或隨機效應對動態面板模型的系數進行估計會導致β的ML參數估計是有偏的，進而扭曲模型詮釋的經濟含義[16]。為了解決此問題，本文使用廣義矩估計(GMM)方法。

霍爾茨-埃金和紐維(Holtz-Eakin & Newey)首次提出一階差分廣義矩估計(DIF-GMM)方法，之后由阿雷利亞諾和邦德(Arellano & Bond)發展完善。該方法首先對原模型進行一階差分變換消除其個體固定效應對回歸結果的影響，再使用被解釋變量的水平滯后項作為差分方程中內生變量的工具變量估計模型系數。然而蒙特卡洛模擬結果顯示，當CHIi，t-1的系數較大或者個體效應波動遠大于擾動項波動時，會出現弱工具變量問題，造成該方法的實際效果不佳。為解決弱工具變量問題，提高系數估計的準確度，阿雷利亞諾和博韋爾(Arellano & Bover)、布倫德爾和邦德(Blundell & Bond)提出系統廣義矩估計(SYS-GMM)的方法，即以一階差分廣義矩估計方法中加入水平方程提高估計效率。阿雷利亞諾和博韋爾在阿雷利亞諾和邦德的基礎上提出可產生T-3個新的矩條件：

E(μitΔyi，t-1)=0 (i=1，2，...，N；t=4，5，...，T)

(11)

因為Δyi2是已知，由此可得：

E(μi3Δyi2)=0

(12)

由此推導出：

E(ZTsysμ*i)=0

(13)

其中，ZTsys為：

(14)

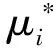
(15)

得出系數的一步系統廣義矩估計量為：

(16)

其中，An為：

(17)

由此推導出兩步系統廣義矩估計量為：

(18)

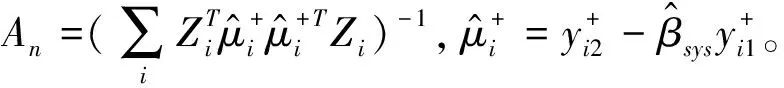
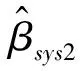
(三) 主要實證結果分析

為有效避免模型偽回歸問題，在開始兩步SYS-GMM估計之前，對短面板數據進行HT檢驗，所有變量均在5%的顯著水平上拒絕原假設，說明回歸樣本數據平穩。

1.人口規模、創新投入對全要素生產率的影響

2009—2018年，京津冀地區城市全要素生產率對城市人口規模、創新投入的回歸結果如表8所示。模型1-1為城市全要素生產率對政府創新投資的回歸，結果顯示，滯后一期的政府創新投資的回歸系數為0.145，在5%的水平上顯著，說明在外商投資和交通運輸客運能力控制變量的作用下，政府前一期的創新投入能夠有效促進城市全要素生產率水平的提升。模型1-2為城市全要素生產率對城市(市轄區)常住人口規模的回歸，回歸結果不顯著，說明人口規模的增加對提升城市全要素生產率作用不明顯，人口集聚效應并未得到釋放。模型1-3為城市全要素生產率對每萬人在校大學生人數的回歸，結果顯示，滯后一期的高水平人才集聚能夠有效改善進城市全要素生產率，回歸系數為0.197，在1%的水平上顯著。模型1-4為城市全要素生產率對企業創新投資的回歸，結果表明企業創新投資對提升整個城市的全要素生產率影響作用不顯著，這可能是因為企業創新投資更多的利益傾向于企業發展，而對整個城市的發展影響相對較小。上述4個子模型回歸結果通過Sargan檢驗，表明回歸結果具有較好的穩健性。

表8 人口規模、創新投入對全要素生產率影響的SYS-GMM估計結果

2.人口規模、創新投入對技術進步的影響

城市技術進步對人口規模、創新投入的回歸結果如表9所示。其中，模型2-1為城市技術進步對政府創新投資的回歸，結果顯示，政府創新投資的回歸系數為0.160，在1%的水平上顯著，而政府創新投入平方項不顯著，但是其系數符號為負，表明從長期來看，政府創新投入對城市技術進步的影響會呈非線性的倒U型關系，短期投資能夠幫助城市實現科技創新，但是若持續投資，政府干預太多，會對城市自身創新發展機制產生擠出效應，讓城市技術呈倒退趨勢。模型2-2為城市技術進步對城市(市轄區)常住人口規模的回歸，回歸結果不顯著，同模型1-2結果保持一致，說明人口規模的增加對提升城市技術進步作用不明顯，人口集聚效應并未得到釋放。模型2-3為城市全要素生產率對每萬人在校大學生人數的回歸，結果顯示，當期和滯后一期的高水平人才集聚能夠有效改善城市全要素生產率，回歸系數分別為3.244和0.215，分別在5%、1%的水平上顯著，高水平人才集聚取對數后的平方項系數為-0.247，在10%的水平上顯著，表明適量人才集聚能夠充分釋放集聚正外部效應，促進城市技術進步。此外前一期的技術進步水平對當期技術水平有較大的影響，回歸系數為0.252，在1%顯著性水平下顯著，表明技術積累同知識積累相類似，都同樣具有 “1+1>2”的集聚效應。模型2-4為城市全要素生產率對企業創新投資的回歸，結果顯示，企業創新投資及其平方項回歸系數分別為0.197和0.054，分別在5%、10%的顯著性水平下顯著，對城市技術進步呈正U型的非線性關系。觀察4個模型的控制變量發現，外商直接投資對提升城市技術進步有很好的正向影響，尤其是模型2-2和模型2-4，回歸系數分別為0.145和0.127，均在1%的水平上顯著，這一現象說明城市發展需與世界相融合，充分吸收先進技術更利于城市技術進步。上述4個子模型回歸結果通過Sargan檢驗，且符合經濟學客觀認知，表明回歸結果具有較好的穩健性。

表9 人口規模、創新投入對技術進步影響的SYS-GMM估計結果

3.人口規模、創新投入對技術效率的影響

城市技術效率對人口規模、創新投入回歸結果如表10所示。模型3-1為城市技術效率對城市人口規模的回歸，其一次項和二次項回歸系數分別為1.210和-0.127，分別在10%的水平上顯著，對城市技術效率呈明顯的非線性倒U型關系，說明人口集聚初期，能提升城市基礎設施及資源的利用效率，集聚正外部效應明顯，隨著人口規模的擴張，正外部效應會逐步被人口規模帶來的負向效應所抵消。模型3-2為城市技術效率對每萬人大學生在校生人數的回歸，其一次項和二次項回歸系數分別為-2.840和0.208，均在5%顯著性水平下顯著，對城市技術效率的影響表現出強烈的正U型相關關系。模型3-3為城市技術效率對政府創新投入的回歸，結果顯示，政府創新投資一次項和二次項回歸系數分別為0.190和-0.046，分別在1%、10%的水平上顯著，與模型2-1(城市技術進步對政府創新投資回歸)回歸結果保持一致。模型3-4為城市技術效率對企業創新投資的回歸，結果顯示，其一次項和二次項回歸系數分別為0.402和0.125，均在1%的水平上顯著，表明很長一段時期內，企業創新投資能夠有效促進城市技術效率的提升，進一步觀察回歸結果發現，交通運輸能力的回歸系數為0.224，在1%的水平上顯著，說明城市交通運輸能力對城市技術效率具有顯著的影響。上述4個子模型回歸結果通過Sargan檢驗，表明回歸結果具有較好的穩健性。

表10 人口規模、創新投入對技術效率影響的SYS-GMM估計結果

4.模型檢驗

兩步系統GMM方法比差分GMM系數估計效果更為準確，一方面是其假設條件更為嚴格。其一要求隨機擾動項εit不存在自相關，使用AR(2)檢驗，若一階序列自相關檢驗拒絕原假設且二階序列自相關檢驗不拒絕原假設，則表明隨機擾動項εit不存在自相關。其二是工具變量有效性問題，運用Sargan檢驗來鑒別過度識別問題，其原假設H0：所有工具變量均有效。從回歸結果可知，所有模型的隨機擾動項εit均不存在自相關問題且Sargan檢驗均接受原假設。回歸模型通過假設檢驗，該動態面板模型使用SYS-GMM估計的結果具有良好的穩健性。

五、主要結論

基于京津冀2009—2018年城市全要素生產率的測算結果和實證檢驗結果，得出以下結論：

第一，京津冀地區全要素生產率逐漸提高，表明在京津冀一體化發展背景下，城市間的競合效應逐漸顯現。進一步分析城市全要素生產率及其分解指數發現，京津冀的全面發展得益于技術進步和技術效率水平的提升，其中，技術進步的邊際貢獻率更高。

第二，常住人口規模與城市全要素生產率和城市技術進步之間未表現出明顯的相關關系。但是就城市技術效率對人口規模的回歸結果來看，其一次項和二次項回歸系數分別為1.210和-0.127，且均在10%的水平上顯著，表明城市技術效率與人口規模呈明顯的倒U型關系。這說明城市發展初期，適量人口集聚能提升城市基礎設施及城市稟賦的利用效率，集聚的正外部效應明顯，隨著人口集聚規模的不斷增加，正外部效應逐步被人口規模帶來的負向效應所抵消，這也與微觀經濟學中，短期生產函數“三階段”模型相吻合，即短期內要想產出最大，其資本與勞動必須實現最佳組合。

第三，人才集聚能顯著提升城市全要素生產率，且存在滯后效應。對全要素生產率的分析結果顯示，當期和滯后一期高水平人才集聚的回歸系數分別為3.244和0.215，且分別在5%、1%的水平上顯著，說明高水平人力資本集聚能夠充分釋放集聚正外部效應，促進城市高質量發展。這也符合組織行為理論的觀點，即人才集聚但資源一定，當人力供給大于就業需求時企業組織內部的競爭力會增強，同時自身的就業壓力也會增加，進而倒逼組織內的人不斷提升自己，則此時會產生更多的正外部效應。

第四，對城市技術進步的分析結果顯示，政府創新投資的回歸系數為0.160，在1%的水平上顯著，但政府創新投入平方項不顯著，且系數的符號為負。這表明從長期來看，政府創新投入對城市技術進步的影響會呈非線性的倒U型關系，短期投資能夠幫助城市實現科技創新，但是若持續投資，政府干預太多，會對城市自身創新發展機制產生擠出效應，讓城市技術呈倒退現象。

基于上述結論，本文提出以下政策建議：第一，制定合理的人才培養和引進政策，促進人才規模多元化擴張。人才集聚對城市發展具有顯著的促進作用，對于經濟欠發達且難以吸引優秀人才遷入的城市，除了要提高人才引進福利外，更要著重完善自身的人才培養體系，加強教育資源投入和教育基礎設施及師資力量建設。對于經濟發達的城市，要重點關注人才是否產生過度聚集現象，并合理引導人才流動。第二，優化城市人才聚集結構，使之與經濟發展重心相匹配。城市發展離不開人才集聚，但不同城市的經濟發展重心和產業結構間存在明顯差異，只有適合城市經濟發展需要的創新型人才集聚才能合理、高效地利用城市資源稟賦，充分發揮人才集聚效應，使城市經濟實現高質量增長。因此應依據各城市不同經濟發展階段和發展重心，合理調控人才集聚結構。第三，優化政府對科技創新領域的資金投入，充分發揮政府的創新引領作用。科技創新是引領發展的第一動力，對于科技創新領域欠發達的城市，地方政府應高度重視科技創新對促進城市經濟發展的重要作用，制定有效的科技創新激勵機制，引導企業對創新技術的研發，提高城市科技創新水平。