行列式在線性代數教學中的應用探討
吳敬源
(吉林建筑科技學院,長春 130000)
1 行列式在線性代數中的重要性
矩陣、向量等內容是線性代數這門學科的重要知識點,是必不可少的運算工具,行列式是學習矩陣的基礎,行列式的很多計算方法可以按相同的原理轉化成計算矩陣的方法。
2 行列式的計算方法
第一,對角線法則。
按對角線法則可得
對于三階行列式,對角線法則的應用相對復雜一些,
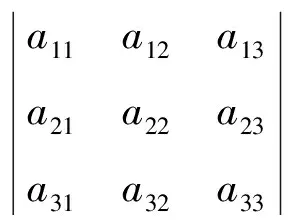
-a11a23a32-a12a21a33-a13a22a31
但是對于四階以上的行列式,對角線法則運算就會相當繁瑣,不適用此運算方法。
第二,n階行列式的定義公式。
由n2個數aij(i,j=1, 2,…,n)構成的代數和
∑(-1)ta1p1a2p2…anpn
其中,t是當行標為自然數列時列表的逆序數,或者當列標為自然數列時行標的逆序數。
例如:證明下列三角形行列式
解:求出展開式中所有可能不為零的乘積項,要使取自不同行不同列的n個元素的乘積不一定為零,第一行只能取a11,第二行只能取a22,第三行只能取a33,…,第n行只能取ann,這樣的乘積項只有一個,就是a11a22a33…ann。由于其列標排列為標準排列,其逆序數為零,所以其前面帶有正號,因此
這種方法常用于行列式中含零比較多的情況,如果行列式中含零較少,則不適用這種運算方法。
第三,以數k乘第j行加到第i行上,記作krj+ri。
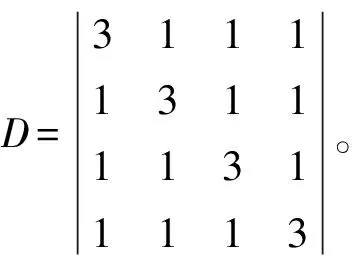
解:


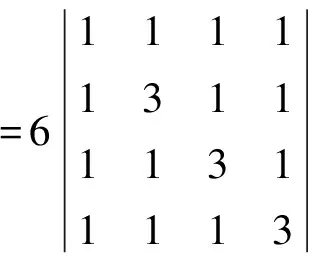
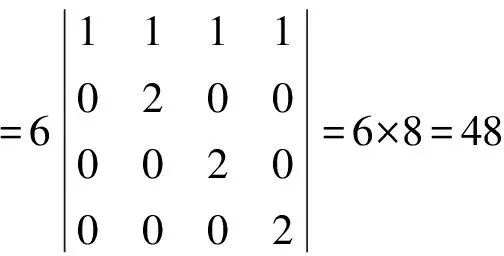
或計算
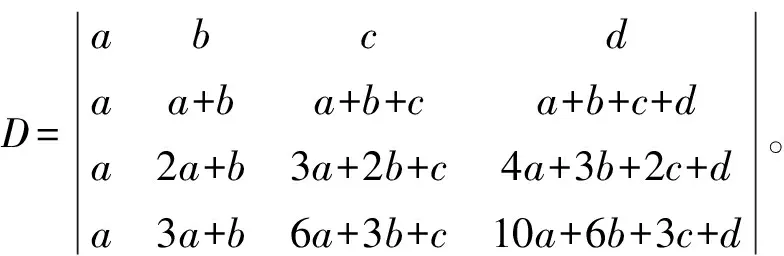
解:
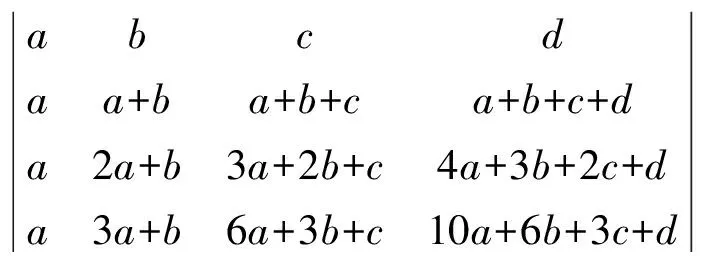
(下一步:r4-r3,r3-r2,r2-r1)
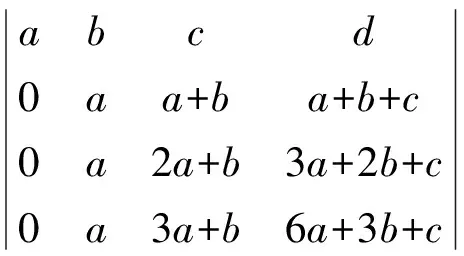
(下一步:r4-r3,r3-r2)
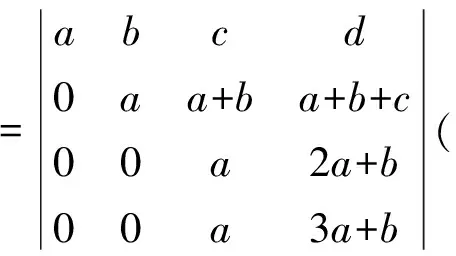
3 提高學生學習行列式興趣的對策
以上三種方法可以解決行列式中遇到的大部分問題。由于部分學生對數學這門學科存在畏懼心理、教學形式比較單一、課堂氛圍枯燥沉悶等原因,導致學生存在學習興趣不高的現象,不利于對知識的理解和記憶。因此,可以在講授知識點時加入聯系實際生活的趣味元素,提升行列式的教學效果。

通過這種形式提高學生的學習興趣,使學生不但學習到理論知識,并能使其應用到實際生活中,從而提高學生的學習效率和學習熱情。
4 結語
線性代數是大部分高校開設的一門基礎課程,具有較強的邏輯性與抽象性,而行列式是線性代數教學中的重要內容。探討了行列式在線性代數教學中的應用,分析了三種行列式的計算方法,提出了提高學生學習行列式興趣的對策,要在講授知識點時加入聯系實際生活的趣味元素,進而提升行列式的教學效果,提高學生的學習熱情和學習效率。

