超導納米線單光子探測器光子響應機制研究進展*

張彪 陳奇 管焰秋 靳飛飛 王昊 張蠟寶 涂學湊 趙清源 賈小氫 康琳 陳健 吳培亨

(南京大學電子科學與工程學院,超導電子學研究所,南京 210023)

超導納米線單光子探測器(SNSPD)已在量子信息、深空激光通信、激光雷達等眾多領域發揮了重要的作用.雖然SNSPD 經過二十年的研究,但其光子響應本征機制還有待完善.深入理解與厘清其光子響應過程是研發高性能探測器的前提與關鍵.現在較為成熟的超導納米線單光子探測器響應理論有熱點模型和渦旋模型.但是這兩種理論都存在一定的缺陷,前者存在截止波長,后者存在尺寸效應,都需要進一步完善.超導相位滑移是超導體的內稟性耗散,有望用于解釋超導納米線單光子探測器的光子響應過程,形成統一完備的理論.這三種模型是對SNSPD 光子檢測理解的不斷深入:熱點模型是一種唯象模型,研究電子-聲子等準粒子體系的相互作用;渦旋模型由Ginzburg–Landau 方程和電磁學方程出發,研究渦旋在超導體中的運動及其帶來的超導態耗散;相位滑移模型是基于量子力學的解釋,研究熱擾動和宏觀量子隧穿引發的超導態耗散.本文綜述了熱點模型、渦旋模型和超導相位滑移的基本概念、發展歷史和研究進展,討論和對比了這三種理論的特點和發展前景,為超導納米線單光子探測器光子檢測理論研究提供參考和借鑒.

1 引言

一個多世紀以前,荷蘭物理學家Onnes[1]在測量金屬汞的剩余電阻時,首次發現超導現象,打開了物質世界的新大門.1933 年,德國物理學家Meissner[2]在測量超導錫單晶球的磁場分布時,發現了超導體的完全抗磁性,即邁斯納效應.在不斷排除與超導電性起因無關的因素后,Bardeen,Cooper 和Schrieffer[3]于1957 年建立起著名的BCS理論,提出電子-晶格相互作用體系,成功解釋了超導電性的起因.1962 年,英國物理學家Josephson[4]在理論上預言了超導電子對隧穿現象,即約瑟夫森效應,并為實驗所證實.超導體的零電阻效應、邁斯納效應、約瑟夫森效應等構成了超導體應用的物理基礎,為超導體創造了巨大的應用價值,促進了諸如超導電纜、超導磁體、超導磁懸浮列車、超導量子干涉儀、超導單光子探測器等應用的蓬勃發展.目前,全世界有近30 家單位開展了超導電子學相關的研究工作,國外著名研究團隊包括美國的MIT(麻省理工學院)、NIST(美國國家標準與技術研究院)和JPL(噴氣推進實驗室),日本的NICT(情報通信研究機構),俄羅斯的莫斯科國立師范大學和歐洲的格拉斯哥大學、TU Delft(代爾夫特理工大學)等.國內開展相關研究的機構包括南京大學、上海微系統所、中國科學院紫金山天文臺、中國科學院物理研究所、西南交通大學、清華大學、天津大學和南開大學等.2017 年,西南交通大學課題組和美國NIST 團隊合作,實現了能量分辨率為220 meV、在1550 nm 波段可分辨7 個光子的微波動態電感單光子探測器(MKID)[5].2017年,紫金山天文臺團隊實現了硅基鋁膜MKID 的8×8 像元集成[6],該探測器的等效噪聲功率低至10–17W/Hz1/2量級.2018 年,中國科學院物理研究所[7]用低通濾波器和高通濾波器級聯的方法,在UHF 頻段實現了超寬帶高溫超導帶通濾波器系統設計,相對帶寬為108%.2020 年,清華大學針對“失蹤重子”問題,聯合國內外多家單位開展了宇宙熱重子探尋者衛星項目[8],計劃使用3600 像素的超導邊沿轉變探測器(TES),對星際間的溫熱氣體在軟X 射線波段進行觀測,該觀測有望為研究星系演化和宇宙大尺度結構提供可靠的觀測數據.

超導納米線單光子探測器(superconducting nanowire single photon detector,SNSPD)作為超導弱電領域的關鍵應用之一,于2001 年由Gol'tsman 等首次報道[9].最近二十年里SNSPD 在實驗上取得了飛速發展,在1350 nm 波段探測效率達到99.5%,在1550 nm 波段探測效率達到98%[10?12],最低時間抖動小于3 ps[13].同時,SNSPD 被廣泛應用到各個領域,包括量子密鑰分發[14]、量子計算[15]、量子表征[16,17]、激光通信[18]、激光測距[19,20]等.2020 年,上海微系統所研究團隊和中科大合作,將SNSPD 應用于遠距離量子通信實驗,創造了光纖量子密鑰分發距離的世界紀錄[21];同年,上海微系統所研究團隊和中科大合作,將SNSPD 應用于構建量子計算原型機“九章”,成功實現了“量子計算優越性”的里程碑式突破[22].2018 年,天津大學研制了彎曲納米線型SNSPD,成功實現了偏振不敏感SNSPD[23].

南京大學自2008 年研制出我國首個SNSPD[24]以來,在國家重大科研儀器項目、973 計劃、重點研發計劃和國家自然科學基金等大力支持下,已研制出系列SNSPD 器件及系統.其中,南京大學研制的單模光纖耦合SNSPD 在1550 nm 波段探測效率超過90%;通過低溫光束壓縮和陣列結構研制的SNSPD 兼具大接收口徑(? >300 μm)和高時間精度(<72 ps)的優點;研制的MoSi 中紅外SNSPD 最長響應波長達到11 μm,在5 μm 波段量子效率超過97%[25];與云南天文臺等合作,利用SNSPD 突破衛星激光測距領域高性能1064 nm探測器瓶頸[20],并于2017 年在國際上首次應用于小空間碎片探測[26]和2021 年應用在月地激光測距[27].另外,南京大學研制的SNSPD 還被應用于激光雷達、生物熒光成像等多個領域[19,28?30],使相關應用取得突破性進展.

在實驗上取得了巨大進展的同時,SNSPD 光子檢測機理方面還有待完善.傳統的熱點(hot spot)模型認為光子輻照納米線產生熱點,電流被擠壓到熱點以外的區域,熱點在電流的作用下持續長大,使熱點周圍的電流密度超過臨界電流密度,使整根納米線失超[31].但是,有理論指出熱點模型預言SNSPD 存在光子檢測的截止波長,這在實驗上現象不明顯[32].渦旋(vortex)模型認為,長波長的光子輻照不足以使納米線產生熱點,而是產生渦旋-反渦旋對(vortex-antivortex pair,VAP),或者導致邊界渦旋穿越納米線,最終導致納米線失超,產生可觀測的電脈沖[33].然而Likharev 的理論表明,渦旋在寬度小于4.41ξ(GL 相干長度,GL:Ginzburg-Landau)的弱連接中不能形成[34].2014 年,Renema 等[35]深入討論了SNSPD 的正常核熱點模型、擴散熱點模型、渦旋成核模型和渦旋穿越模型,他們發現在光子探測過程中,準粒子擴散和渦旋同時發揮重要作用,渦旋穿越模型是最接近實際情況的理論.基于相位滑移(phase slip)的SNSPD檢測理論最近幾年還處于探索階段.該理論認為,受到熱擾動或者宏觀量子隧穿(macroscopic quantum tunneling,MQT)的影響,在納米線相干長度的區域內,超導波函數的幅值突然降為0,伴隨著相位發生2π 突變,導致納米線出現可觀測電阻[36].相位滑移理論最初用來解釋超導電性的耗散,目前有望用于解釋SNSPD 的光子響應機制,同時能避免熱點模型和渦旋模型的缺陷.

衡量SNSPD 性能的重要指標之一是系統探測效率SDE (system detection efficiency),一般認為SDE 受耦合效率、吸收效率和量子效率的影響:SDE=耦合效率×吸收效率×量子效率[37].耦合效率指的是光子在到達器件之前經歷的吸收、散射和反射等引起的損耗,吸收效率指的是SNSPD對光子的吸收能力,取決于器件的材料和幾何結構,量子效率指的是SNSPD 吸收一個光子后產生電脈沖的概率.對SNSPD 光子檢測機理的研究有助于加深我們對吸收效率和量子效率的理解,進而提高SNSPD 在探測效率、時間抖動、暗計數等方面的綜合性能.目前有很多種材料被用來制備SNSPD,如NbN、WSi、MoSi 等,這些材料具有不同的材料參數,如超導轉變溫度、GL 相干長度、電子態密度等,如果不能深入理解超導檢測機制和這些參數之間的關系,我們就很難找到最佳的材料和設計方案來制備具有特定性能的SNSPD.此外,對檢測機制的深入理解也有助于我們制備極限性能的SNSPD,將SNSPD 用于有高性能需求的領域.

深入理解SNSPD 光子檢測機制,厘清SNSPD光子響應過程,是發展新型SNSPD 器件的前提,是研制性能優異SNSPD 器件的關鍵.2021 年適逢第一個SNSPD 報道的二十周年,本文綜述了SNSPD 熱點模型、渦旋模型和超導相位滑移模型的基本概念、發展歷史和研究進展,為SNSPD 光子檢測理論的研究提供參考和借鑒.

2 SNSPD 光子探測模型

2.1 熱點模型

1971,Testardi 等[38]首次在實驗上發現超導體對光學波段的輻射敏感,他們使用激光輻照處于超導態的鉛膜,發現激光能破壞其超導電性,這種效應不能簡單的使用熱效應來解釋.實驗使用的鉛膜厚度為27.5 nm,放置在液氦杜瓦中,使用脈沖激光器照射鉛膜,測量其電阻值變化.實驗發現當有脈沖輻照到鉛膜上時,它的電阻會發生突然的增大,如圖1(a)所示.

Testardi 將這種現象解釋為:超導體吸收的光子能量導致其產生一種非均衡態,產生熱激發的準粒子(quasiparticle),這種準粒子的溫度比庫珀對(cooper pair)高.超導體經過以下一系列過程可以重新獲得均衡態:1)電子-電子相互作用和電子-聲子相互作用,導致準粒子非彈性散射;2)聲子產生新的準粒子;3)準粒子重新結合;4)聲子將能量傳向襯底,最終導致能量耗散.

熱點的概念最初由Skocpol 等[39]于1974 年在研究超導微橋的自熱效應時提出.Skocpol 認為熱點的形成是導致超導微橋I-V曲線出現遲滯現象原因,即對于相同的電壓,由于電壓變化的歷史過程不同,超導微橋的電流也不一樣,圖1(b)展示了熱點區域上的溫度變化.借助熱點概念,1995 年,Semenov 等[40]提出了一種雙溫模型,解釋超導薄膜的光響應過程.這個模型引入了隨溫度變化的電子亞系統和聲子亞系統,其溫度狀態可以通過解下面兩個相互耦合的熱方程得到:

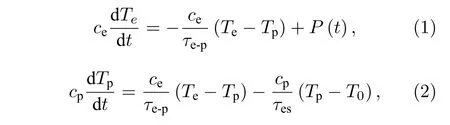
其中:ce,cp是電子、聲子的比熱容;Te,Tp是電子、聲子的溫度;τe-p是電子-聲子相互作用時間;τes是聲子弛豫時間;T0是襯底溫度;P(t)是單位面積薄膜吸收的輻照功率強度.(1)式描述了電子吸收能量與電子-聲子熱傳遞達到平衡,(2)式描述了聲子吸收能量和聲子向襯底傳遞熱量達到平衡,以NbN 薄膜為例,整個體系的平衡狀態可以由圖1(c)說明.

1996 年,Kadin 等[41]進一步把上述雙溫模型近似的寫成如下的熱流方程:

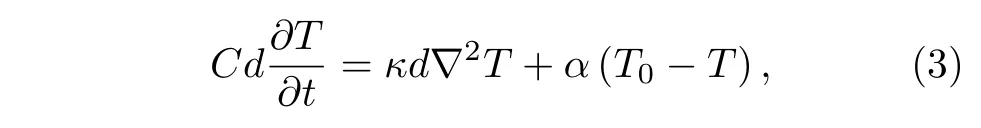
其中,C是電子和聲子的比熱容之和,d是薄膜厚度,T是薄膜的溫度,T0是襯底的溫度,k是薄膜的熱導率,α是薄膜和襯底之間的邊界熱導.以上公式可以解出光子吸收產生熱點的大小大約為幾納米到幾十納米,因此在制備納米線的時候,需要把納米線的寬度也制備為這個量級,以達到單光子檢測的目的.

2001 年,Semenov 等[31]針對SNSPD 探測原理首次提出了熱點模型:入射光子的能量遠大于材料的超導能隙,破壞了大量的庫珀對,引發了數量分布不均的準粒子,在超導薄膜中形成熱點.薄膜超導區域寬度減小,超導電流被排斥到熱點以外的納米線區域,此時熱點區外的電流密度可能會超過破對電流(depairing current,Idp)密度,超導狀態變得不穩定,引發電壓響應.Semenov 從理論上證明,使用亞微米超導線條有望實現可見光和近紅外單光子的檢測.Semenov 將準粒子的集中程度用函數C描述為[31]:

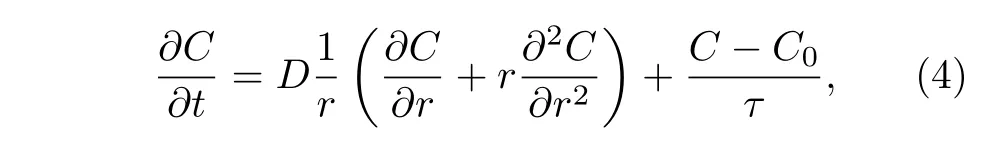
其中,C(r,t)是空間r和時間t的函數,r是準粒子到光子吸收區域的距離,1/τ是準粒子通過耦合或者聲子逃逸到襯底的弛豫時間,D是準粒子擴散常數,C0是庫珀對沒有發生解耦合時的集中函數初值,由環境溫度決定.通過求解(4)式,可以得到C(r,t)的表達式為

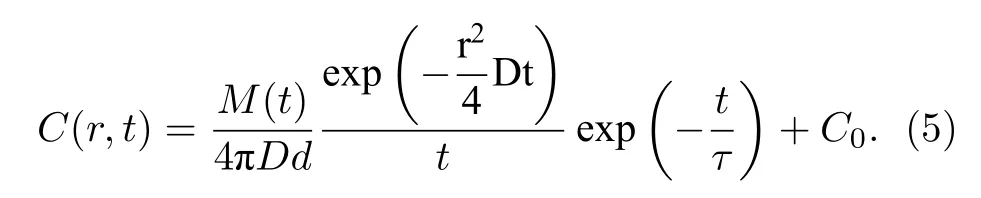
在亞微米超導線條的量子檢測機制后,2001 年,Gol'tsman 等[9]在實驗上首次制備出200 nm 寬、1.2 μm 長的氮化鈮納米線,也就是世界上第一個SNSPD.器件工作在液氦溫區,在0.8 μm 波段得到了20%的量子效率,圖2 是Gol'tsman 將熱點模型用于解釋納米線光響應的原理圖.

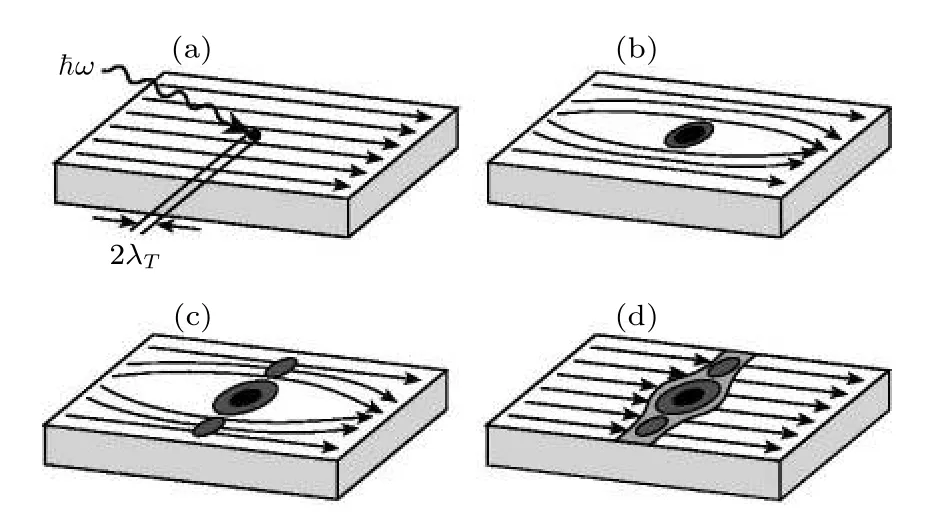
圖2 Gol'tsman 等[9]于2001 年首次制備出SNSPD,將熱點模型應用在解釋其光子響應,(a)—(d)分別表示光子入射、熱點形成、熱點長大、納米線全部失超Fig.2.Gol'tsman et al[9].fabricated SNSPD for the first time in 2001,and applied the hot spot model to explain its photon response.(a)–(d) denote photon incidence,hot spot formation,hot spot growth and thoroughly shut down of the nanowire,respectively.

2005 年,Semenov 等[32]在之前工作的基礎上提出了改進的熱點模型(refined hot-spot model),進一步考慮了準粒子的貢獻,計算了熱點周圍準粒子的密度變化.該模型在一個圓柱形區域內計算了準粒子的密度,認為當最大非平衡準粒子數達到平衡值時,器件的量子效率出現截止.Semenov 證明,由于正常態區域的大小隨著光子能量的增加而增大,因而熱點模型預測納米線的量子效率存在一個截止波長.同時,Semenov 發現電阻態的弛豫時間與光子能量存在一定關系,因此可以實現光子能量分辨的單光子探測器件.

2007 年,Yang 等[42]在熱點模型基礎上提出了一維的電熱模型,考慮了焦耳熱的影響,證明了熱是引起納米線失超、產生電脈沖的原因.該模型認為影響探測器恢復時間的主要因素是納米線的動態電感,與納米線串聯一個電阻可以加快納米線的恢復;同時提出,如果串聯的納米線電阻過大,會導致納米線進入閂鎖態,這個過程可以使用電熱模型進行模擬:

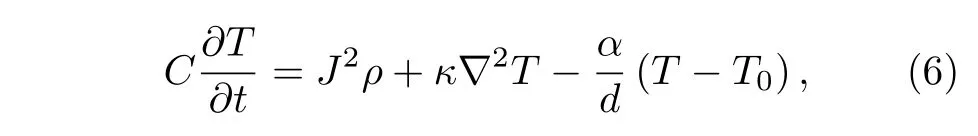
其中,J表示電流密度,ρ表示電阻率.與(3)式相比多了焦耳熱的項.

2017 年,Vodolazov[43]研究了超導納米線吸收近紅外和可見光波段單光子后電子和聲子的動力學行為,進一步提出了微米尺寸的超導微橋對單光子探測的可能性.Vodolazov 發現,在Tc溫度下,電子比熱容Ce和聲子比熱容Cph比值(Ce/Cph|Tc)越大,光子能量向電子傳輸的比率就越大,電子在熱點形成的最初階段熱化進程加快,對于Ce/Cph|Tc?1 和擴散系數D～ 0.5 cm2/s 的超導體,其熱化時間τth小于1 ps.Vodolazov 的分析結果表明,對于幾微米寬的超導微橋,如果其超導臨界電流超過0.7Idp,并且Ce/Cph|Tc≥ 1,那么這種微橋對近紅外和可見光波段的單光子也具有檢測能力,這為我們設計和制備超導微米線單光子探測器提供了理論指導,對于深入理解SNSPD 探測機理也具有重要價值.

2.2 渦旋模型

渦旋結構是一種非均勻磁化的穩定磁結構,由中心渦核區域(vortex core,VC)和外圍區域兩部分構成,容易在微米或亞微米尺寸的圓盤形或橢圓形薄膜中形成[44].在尺寸受限的磁性薄膜體系中,由于交換場和退磁場之間的相互競爭,在微米或亞微米尺寸的圓盤形或橢圓形薄膜中易形成磁渦旋結構(magnetic vortex).在圓盤或橢圓樣品邊界區域,由于退磁場的作用,磁矩在薄膜面內沿邊界走向旋轉排列,以實現退磁能的能量最低狀態;但在渦核區域,相鄰旋轉磁矩間的夾角較大,導致交換能迅速提升,體系的退磁場和交換場之間的競爭促使渦核區域的磁矩指向垂直于膜面的方向.磁矩的卷繞在序參量空間的投影數目q決定了拓撲渦旋態:q=1 為渦旋態,q=–1 為反渦旋態.由于超導體存在倫敦穿透深度,磁場可以進入超導體的一部分區域,因而對于超導薄膜,渦旋是引起超導耗散的可能因素,渦旋常被用以解釋SNSPD 的暗計數和光響應,以下介紹基于渦旋的SNSPD 響應機制的發展歷史和存在的缺陷.

1990 年,Kadin 等[33]提出一種基于二維超導體的新型量子探測機制,即渦旋-反渦旋對(VAP)模型.該模型認為,超導薄膜吸收光子后,在薄膜上形成一個VAP,如圖3(a)和圖3(b)所示,在偏置電流的作用下,這個VAP 被拆散,此過程導致在超導薄膜上形成一個電阻態.Kadin 等認為可以通過檢測這個電阻態來檢測紅外光子,但并沒有給出具體的實現方案,事實上該模型中二維超導體中的電阻態在實驗上難以直接檢測.

2011 年,Bulaevskii 等[45]提出了基于渦旋穿越的超導薄膜耗散機制,認為渦旋是引起超導納米線暗計數和光子響應的主要因素,如圖3(c)和圖3(d)所示.Bulaevskii 討論了3 種臨近Ic的可能耗散機制:1)納米線中自發形成的正常態帶狀區域,同時伴隨著2π 的相位滑移.2)在納米線的一端自發形成的渦旋穿越到納米線的另一端,引起電壓響應.3)納米線中心自發形成的渦旋-反渦旋對的破對,并且在洛倫茲力的作用下往相反的方向運動,或者在納米線兩端自發形成的渦旋對,運動到納米線的中心湮滅.在高偏置電流的時候,渦旋可以直接穿越納米線引發響應;或者當偏置電流略低時,在光子入射的協助下渦旋發生穿越,引起響應.

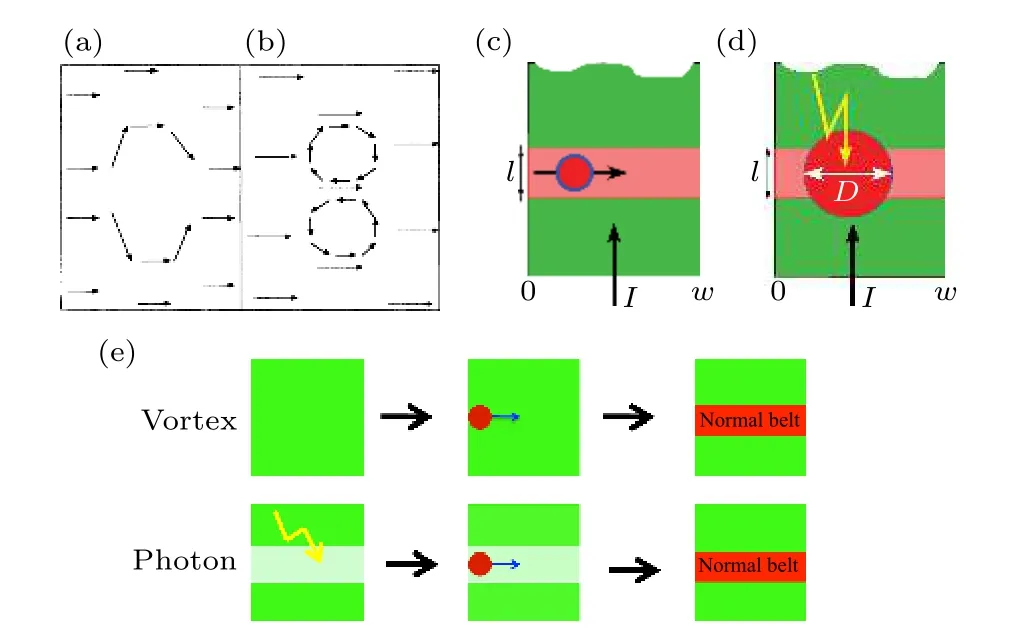
圖3 渦旋模型的發展 (a),(b)渦旋周圍的超導電流分布[33],(a)單個渦旋將電流擠壓到周圍,中間的超導態被抑制,(b)渦旋-反渦旋對,可能形成于較高的偏置電流;(c),(d)基于渦旋穿越的超導薄膜耗散機制[45],(c)單渦旋穿越,(d)光子輔助渦旋穿越模型.兩種耗散都可以使SNSPD 產生可觀測的電壓響應;(e)上圖表示沒有光子時,渦旋穿越導致暗計數形成;下圖表示光子入射導致局部熱點形成,隨后引發渦旋穿越導致響應[46]Fig.3.The development of the vortex-based model:(a),(b)The supercurrent distribution around the vortex[33],(a) current diverting around the region with depressed superconductivity on the scale of the vortex-core area,(b) closely spaced vortex pair oriented properly in near-critical applied current;(c),(d) sketch of a segment of the strip in the presence of a bias current[45],(c) a single vortex causes a hot crossing,(d) A single photon creates a hotspot and induces a subsequent hot vortex crossing.Both processes result in detectable voltage in SNSPD;(e) Top:thermally excited vortex crossing and subsequent formation of a normal-state hot belt across the strip width resulting in a dark count.Bottom:an incident photon creates a hot spot across the superconducting strip,followed by the thermally induced vortex crossing[46].

2012 年,Bulaevskii 等[46]在之前的工作基礎上,進一步提出SNSPD 渦旋輔助的光子響應模型.模型認為,SNSPD 的光響應是由偏置電流下的亞穩態轉變為正常態引起的.論文討論了SNSPD 的探測事件的3 個可能過程:1)具有高能量的單個入射光子,足以打破足夠多的庫珀對,從而在納米線的整個寬度上形成一個電阻態帶,此即直接光子計數;2)在沒有光子入射的情況下,熱激發的單個渦旋從納米線一側穿越納米線,觸發納米線由超導態向正常態轉變,此即暗計數;3)一個能量不足的單光子入到射納米線,引起局部電阻態,降低了納米線超導電性,隨后引發單個渦旋從納米線一側穿越,此即渦旋輔助單光子計數.后兩種過程如圖3(e)所示.Bulaevskii 認為,垂直于納米線平面的磁場不會影響光子形成熱點,但它會導致渦旋穿越的速率增加.理論結果表明,通過施加磁場,可以表征渦旋穿越的能量勢壘,鑒別暗計數和渦旋輔助光子計數的來源.

但是渦旋模型也存在一定不足.1979 年,Likharev[34]在理論上證明,當弱連接的寬度小于4.41ξ時,渦旋不可形成.然而納米線寬度相當小時,在實驗上卻能觀察到光子響應.如Marsili 等[47]使用NbN 薄膜制備了寬度為30 nm 的SNSPD,在5 μm 波段獲得了2%的探測效率;南京大學2021年報道,基于30 nm MoSi 納米線研制的SNSPD,在1—5 μm 波段均獲得了飽和量子效率,在5 μm波段的內量子效率超過97%[25].此外,目前還沒有文獻報道隨著納米線的尺寸減小,SNSPD 探測效率會存在截止,因而關于渦旋的尺寸效應問題需要進一步的研究和完善.

2.3 不同理論之間的討論

2013 年,Renema 等[48]使用一種叫量子探測器層析(quantum detector tomography,QDT)的分析方法,討論了SNSPD 熱點模型、擴散熱點模型和漲落協助模型等三種模型.這種方法主要思想為:固定探測器的探測效率,比如1%,研究此時偏置電流Ib和入射光子能量E之間的關系,這種光子能量-偏置電流(energy-current)的依賴關系是研究探測機理的一個關鍵方法.使用這種方法,Renema得到了探測效率的歸一化曲線,如圖4(a)所示.

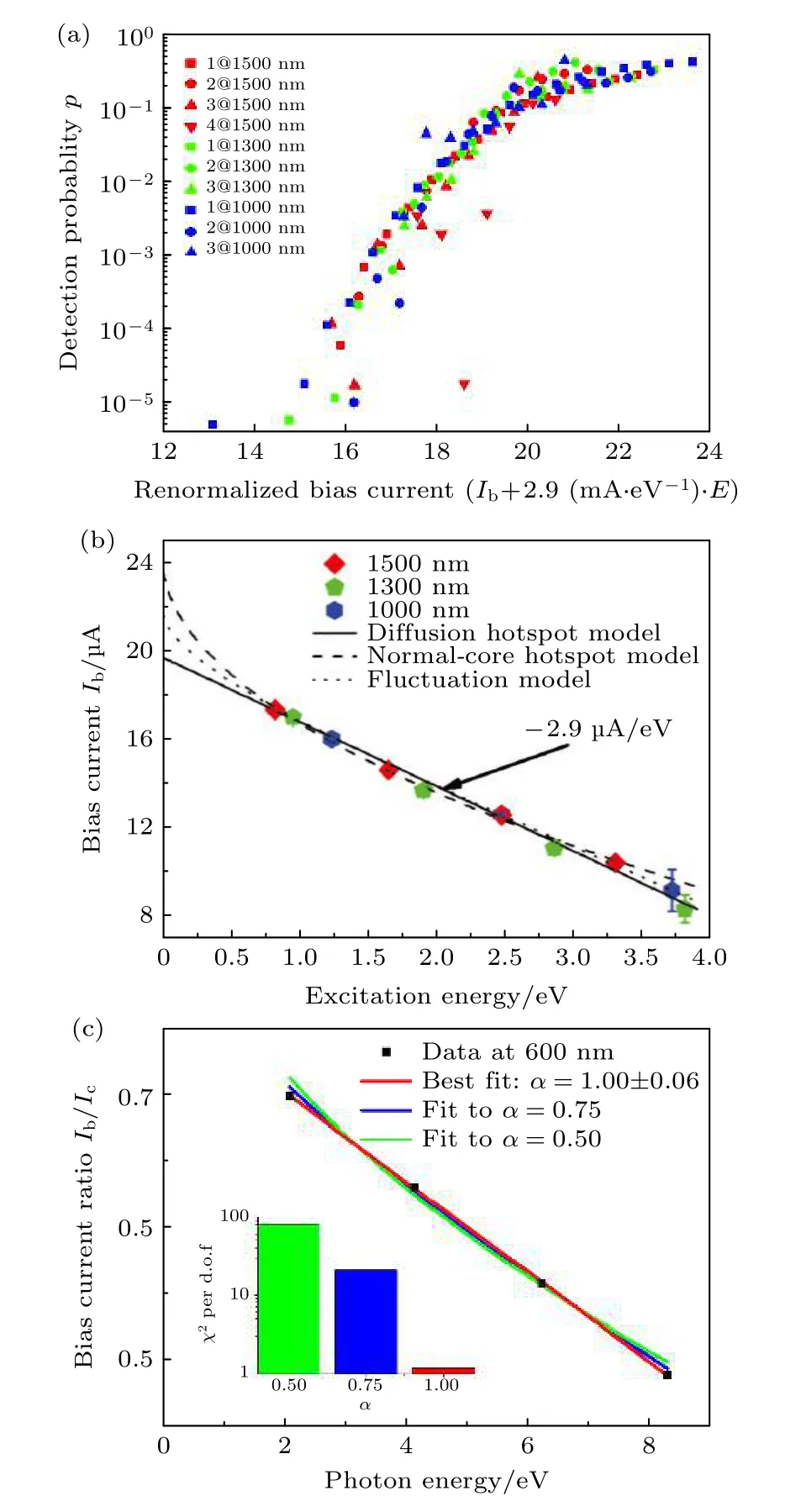
圖4 不同理論之間的討論 (a)探測器層析法得到的SNSPD 響應歸一化曲線,不同符號代表了不同的光子數響應模式和不同的入射波長[48];(b)熱點模型、擴散熱點模型和漲落協助模型對實驗的擬合結果,結果顯示擴散熱點模型具有最好的擬合效果[48];(c)不同模型對實驗數據的擬合曲線,結果表明擴散熱點模型是最有可能的結果[35]Fig.4.Discussions on various theories:(a) The universial detection curve of SNSPD utilizing the detector tomography,different symbols representing corresponding photon number and wavelength[48];(b) the fit of experimental data of the diffusion hotspot model,the normal-core hotspot model and the fluctuation model.It turns out that the diffusion hotspot model fits best to the data[48];(c) different models fitting to the experimental data and the diffusion hot spot model turns out to be the most probable one[35].

熱點模型、擴散熱點模型和漲落協助模型三種模型不僅在機制上有區別,而且在相同的探測概率下,偏置電流和光子能量之間的依賴關系也有區別.對于熱點模型,熱點被認為是一個圓柱體,其半徑和入射光子能量的平方根成正比,因而達到最大探測概率所需要的Ib與E的平方根呈負相關關系,可以由(7)式描述[49]:

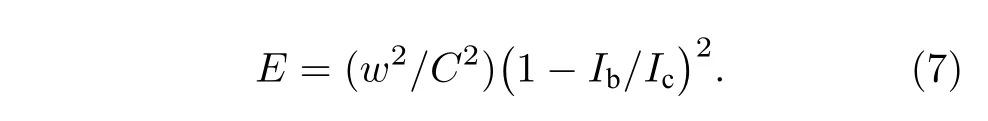
擴散熱點模型(diffusion-hotspot model)同時考慮了準粒子擴散帶來的超導電性降低和熱點的作用,認為熱點的大小和準粒子的擴散距離有關,指出達到最大探測概率所需要的Ib與E呈線性關系[50]:

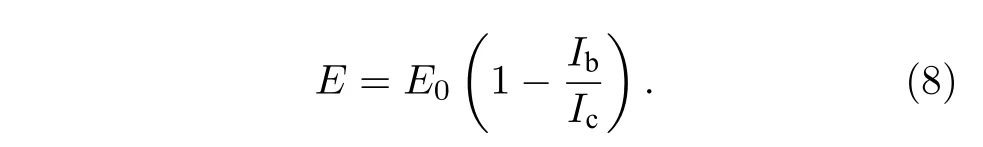
熱點和擴散熱點模型都預言了隨著光子能量降低,SNSPD 探測效率會存在一個截止波長,即波長大到一定程度后,探測效率降為零,但是這在實驗上并沒有觀察到.為了解釋這種現象,Gurevich等[51]提出了漲落協助探測模型(fluctuation-assisted detection models).漲落協助模型認為光子的作用是降低了超導能隙,然后引起熱激發的漲落,如渦旋-反渦旋對破對,或者單個渦旋穿越,由如下關系描述:

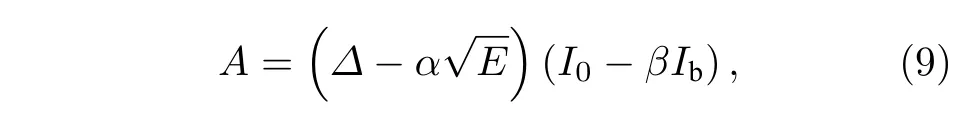
其中,A和α是實驗的擬合參數,I0和β是幾何因子的線性化參數.這個關系式可以解出E和Ib符合雙曲關系,也即E與Ib的關系式中,E的指數在0.5 和1 之間,這個指數大小剛好在熱點模型和擴散熱點模型之間[32,45].圖4(b)展示了這三種模型對實驗數據的擬合[48],結果顯示擴散熱點模型具有最優的擬合效果.

使用QDT 法測量超導納米線的光子能量-偏置電流關系,進而探究SNSPD 的光子響應機理,許多實驗得到了看似矛盾的結果.對于NbN 材料,Renema 等[35]基于220 nm 寬的SNSPD,在0.75—8.26 eV 光子能量波段觀察到了線性關系的實驗結果,而Wang 等[52]基于30—140 nm 寬的SNSPD,在0.73—2.43 eV 光子能量波段觀察到了非線性實驗結果.這種矛盾的實驗結果也存在于不同材料制備的SNSPD 中.對于MoSi 器件,在0.61—1.65 eV光子能量波段,光子能量-偏置電流關系都是非線性的[53];對于WSi 器件情況則更為復雜,探測機理只與總的光子吸收能量有關,而與光子能量分布無關,只有在總吸收光子能量超過0.8 eV 時,光子能量-偏置電流才表現為線性關系,反之光子能量-偏置電流的關系變為非線性[54].由此看來,SNSPD的材料性能、幾何尺寸,甚至入射的光子能量都會對光子能量-偏置電流關系產生影響,進而影響我們對SNSPD 探測機制的理解.這些實驗結果表明,只考慮準粒子擴散的模型不能準確描述SNSPD的實驗現象,擴散熱點模型需要進一步完善.

渦旋在SNSPD 檢測機制中扮演非常重要的作用.2014 年,Renema 等深入探討了SNSPD 的4 種主流響應機制:正常核熱點模型(normal-core hot spot model)、擴散熱點模型(diffusion-based hot spot model)、渦旋成 核模型(vortex nucleation model)和渦旋穿越模型(vortex crossing model).簡化來看,可使用I=I0+γEα來描述所有模型:對于正常核熱點模型,α=0.5;對于擴散熱點模型,α=1;對于渦旋模型,情況變得復雜,但是可以近似認為,對于渦旋成核模型,α=0.5,對于渦旋穿越模型,α=0.75.對實驗數據進行擬合,發現α=1是最佳的擬合結果,說明擴散熱點模型對實驗數據的解釋最為合理[35],圖4(c)展示了這4 種模型的擬合結果.Renema 認為,SNSPD 的探測效率受溫度影響的原因,不是因為超導臨界電流,而是因為與電流相關的渦旋破對,準粒子擴散與渦旋同時影響光子探測事件.2015 年,Vodolazov 等[55]使用外加磁場研究了SNSPD 的光子檢測機理,實驗結果表明,對于波長為450 nm 的光子,熱帶模型(hot belt model)不能解釋光子計數率的磁場依賴現象;也不能解釋當磁場增加時,在450—1200 nm 波段觀察到的光子計數率下降的現象.熱帶模型認為超導納米線吸收光子后,在整個納米線寬度范圍內超導序參量發生了部分抑制.使用渦旋熱點模型(vortex hot spot model)可以對實驗現象進行解釋,即認為在光子誘導的熱點區域內產生了渦旋成核或者渦旋穿越.這個實現結果進一步證實了渦旋在SNSPD 光子檢測過程中的重要性.

3 超導相位滑移與SNSPD 光子響應機制

3.1 超導相位滑移簡介

實驗發現,超導體在臨界溫度Tc以下,即使接近絕對零度,仍存在一定的剩余電阻,這樣的超導體制成的電流環,其中的電流會逐漸衰減,不能永遠持續.此外,在觀察超導體的電阻-溫度(R-T)曲線時,總是能發現曲線具有一定的超導轉變寬度,從幾十mK 到幾K 不等.理論上一般把這類現象解釋為由超導體的不均勻性導致的:在超導體的不同位置其Tc略有差異,導致轉變寬度的產生.一種比較深入的解釋為:由于超導序參量的內稟性波動,即相位滑移(phase slip),導致了超導轉變區域的展寬,這種波動在橫截面積較小的超導體中,即超導納米線等一維超導體,表現得更為明顯.相位滑移可以瞬間破壞超導體不同部分的宏觀相干性,導致超導電流的能量轉化為電磁輻射和焦耳熱,進而導致超導體能量耗散,使其產生了可觀測的電阻.以下內容主要介紹超導相位滑移基本概念和發展歷程.

1967 年,Little[36]在研究細超導環中電流衰減的時候,首次提出相位滑移概念.Little 認為超導體局部的序參量幅值受限于熱擾動,當熱擾動強到足夠使序參量的幅值降為零時,納米線局部區域就表現出非零的電阻.這種熱激發的相位滑移(thermally activated phase slips,TAPS)可以發生于任何溫度不為0 K 的環境,下面介紹Little 的推導過程.

考慮一維超導體的Ginzburg-Landau 方程表述的自由能:

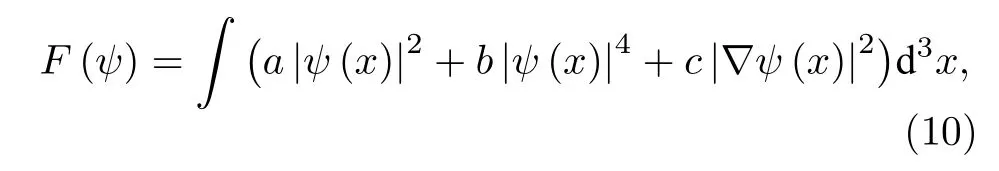
其中,波函數Ψ(x)是超導序參量的波函數,超導序參量指的是超導體中,處于超導態的電子與全部電子數比值.由于任何體系都有把能量最低化的傾向,把自由能方程最小化,可以得到歸一化超導序參量波函數:

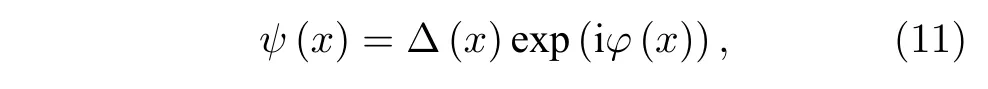
其中,?(x)是幅值,φ(x)是相位,這些最小化的自由能描述了超導體最有可能的存在形式.上述方程指出,一維超導體的GL 序參量,在沿著納米線方向上,受相位參數和幅值參數的影響.由于超導電流與相位的梯度成正比,電流的改變引起了相位參數在空間上的改變,導致序參量在虛部、實部、納米線方向組成的三維空間中呈螺旋狀分布,如圖5(a)所示.沿著x方向,序參量每發生一圈的改變,就對應相位發生2π 的改變.

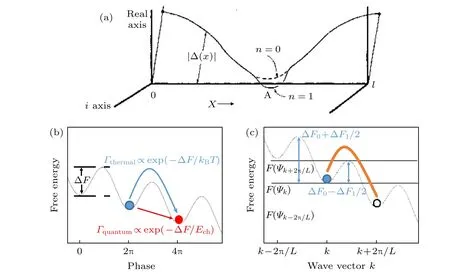
圖5 熱激發相位滑移 (a)復變函數Ψ(x)隨x 的變化.這是2 種可能情況:A 點附近,Ψ1(x)在復平面上環繞一周,Ψ0(x)沒有發生環繞[36];(b)兩種主要的相位滑移過程:TAPS(藍色部分,自由能翻越勢壘)和QPS(紅色部分,自由能隧穿勢壘);(c)自由能F 與波矢k 的關系.當不存在電流時勢壘是對稱的,都等于?F0.當有電流在納米線中流動時,相位滑移勢壘將變得不再對稱Fig.5.Thermally activated phase slips:(a) The order parameter Ψ(x) which is complex is drawn as a function of position.Two possible confgurations are shown.Near A,Ψ1(x) makes an excursion round the Argand diagram while Ψ0(x) does not[36];(b) two major processes of phase slip,the TAPS (blue line,the free energy changes it’s quantuam state by jumping over the energy barrier)and the QPS (red line,the free energy changes it’s quantuam state by tunneling to another potential minimum);(c) free energy F and wave vector k.In the absence of bias current,the energy barrier between adjacent energy minima is identical and equal to ?F0.The barrier becomes asymmetric at a small current.

由于序參量在空間中呈螺旋狀分布,因此GL自由能呈現出周期性的最小值.相位滑移就是指超導態在不同的最小GL 自由能中跳躍的現象:在超導相干長度的空間距離上,由于熱漲落或者宏觀量子隧穿的影響,超導序參量在相鄰區間上的相位發生了2π 的改變,使GL 自由能在相鄰的最小值上發生了躍變,在這個過程中,超導材料產生了可觀測的電阻.

與約瑟夫森結類似,我們可以繪制出自由能與相位的依賴關系,即所謂的“電流傾斜搓衣板勢能”(current-tilted washboard potential),如圖5(b)所示.一般認為,相位滑移具有2 種激發方式:TAPS(圖中藍色過程)和宏觀量子隧穿引起的量子相位滑移(quantum phase slips,QPS,圖中紅色過程).TAPS 一般發生在臨近Tc的溫區,QPS 在幾乎所有低于Tc的溫度下都能發生;TAPS 導致自由能翻過勢壘,QPS 導致自由能發生隧穿.

根據Little 的理論,TAPS 引起的電阻可以寫為如下形式[36,56]:

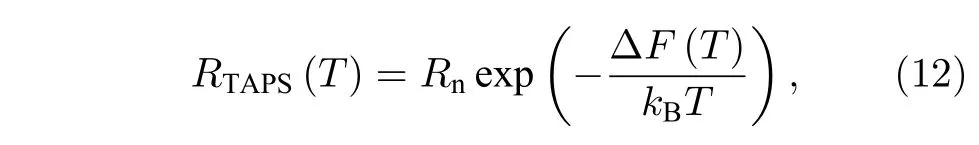
其中:Rn是常溫電阻,可以看出,溫度低于Tc時,納米線電阻隨著溫度降低呈指數衰減;?F(T)是超導凝聚能,即TAPS 過程需要翻越的能量勢壘.?F(T)可以寫成[56]:

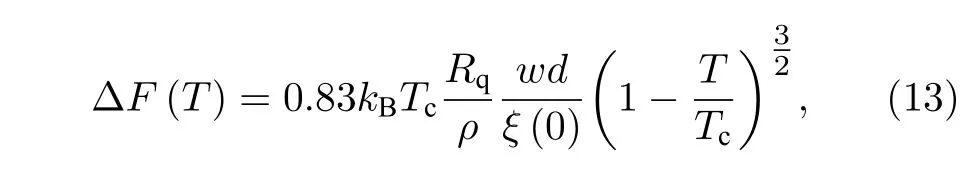
其中:Rq=h/(4e2)=6.5 kΩ 是量子電阻,其中h是普朗克常量,e是元電荷量;ρ為材料電阻率,w為線寬,d為厚度,這些值可以由常溫電阻RN代替:RN=ρNL/σ,σ=wd為橫截面積,ξ(0)為0 K 時的GL 相干長度.(13)式適用于T>0.7Tc的溫區.

Little 的想法可以根據以下推導進行驗證[57]:超導納米線能發生相位滑移的基本單元為一個小線段,這個線段長度為相干長度ξ(T).對于每個基本單元,納米線要么是超導態,要么是正常態.由于相位滑移持續的時間通常在皮秒量級,很難測量出一次相位滑移產生的電阻值,因此實驗中測量到的是單位時間內由大量相位滑移事件導致的“時間平均電阻值R(T)”.假設相位滑移嘗試頻率(attempt frequency)為Ω0,序參量的弛豫時間為τ,二者相互關聯,即Ω0=1/τ.根據Arrhenius 定律,相位滑移頻率ΩPS=Ω0exp(–ΔF/(kBT)),因而每個相位滑移線段每秒鐘能發生相位滑移、表現為正常態的時間占比f=τΩPS=exp(–ΔF/(kBT)),表現出超導態的時間占比為1–f.每個基本單元的常態電阻為Rln=Rnξ(T)/L,其中L是納米線總長度,Rn是整個納米線的常溫電阻.每個基本單元的時間平均電阻值Rt(T)=Rlnf+R0(1–f),R0=0 表示的是超導態的納米線電阻,因此整個納米線時間平均電阻值可以寫成每一基本單元的時間平均電阻值×總的基本單元數L/ξ(T),即R(T)=Rt(T)×L/ξ(T)=Rlnf×L/ξ(T)=Rnξ(T)/Lf×L/ξ(T)=Rnf=Rnexp(–ΔF/(kBT)),即(12)式.

3.2 LAMH 理論

LAMH 理論在Little 的基礎上更精確地計算了TAPS 的勢壘.在納米線的兩端,恒定的外加電壓持續增加納米線兩端的相位差,提高了流經納米線的超導電流.Langer 和Ambegaokar[58]假設,當外加電壓對相位差的增加速率和相位滑移引起的相位差減少達到相同的速率時,超導體達到穩態.類似于交流約瑟夫森效應,可以建立超導納米線兩端的電壓差?V與相位滑移速率Γ之間的關系[4,59],即相位滑移的相關的約瑟夫森關系:

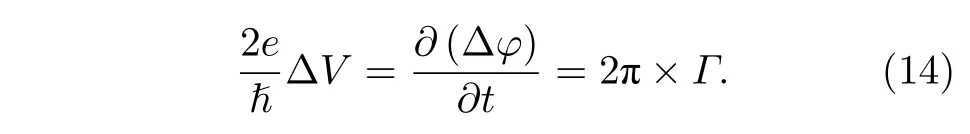
兩個最小自由能之間的勢壘為?F,TAPS 能以一定的概率翻越勢壘,這個概率正比于Langer 與Ambegaokar 計算了在零電流極限下的自由能勢壘為[58]:

其中:σ為納米線的橫截面積;ξ(T) 是相干長度,ξ(T)0.85(lξ0Tc/(Tc?T))0.5,l是電子的平均自由程,ξ0是BCS 理論的0 K 相干長度;gn?gs是正常態與超導態的自由能密度差,其中N(0)是費米面上的態密度.?F0代表了超導納米線的最小體積凝結能,即一個相干長度對應體積的凝結能.

當有外加電壓時,存在電流在納米線中流動,正向和負向相位滑移勢壘?F變得不對稱,降低電流的波動變得比增加電流的波動更容易發生[58],如圖5(c)所示,使波矢k發生±2π/L改變的勢壘為

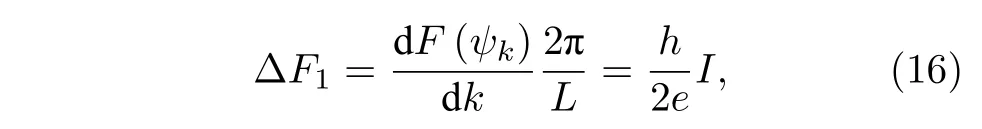
其中,?F1是超導體相位發生2π 的突變時,以電磁輻射形式釋放的能量,也是相位滑移時外界供給的能量.結合(14)式,?F1=IV?t=I×/(2e)×?φ=Ih/(2e),?φ=2π 恰好就是相位滑移的物理本質.

相位滑移引起自由能降低的頻率Γ–和自由能增加的頻率Γ+是不對稱的,一般來說Γ–>Γ+,二者的差值可以估計相位滑移頻率Γ的宏觀表現,由以下關系描述:

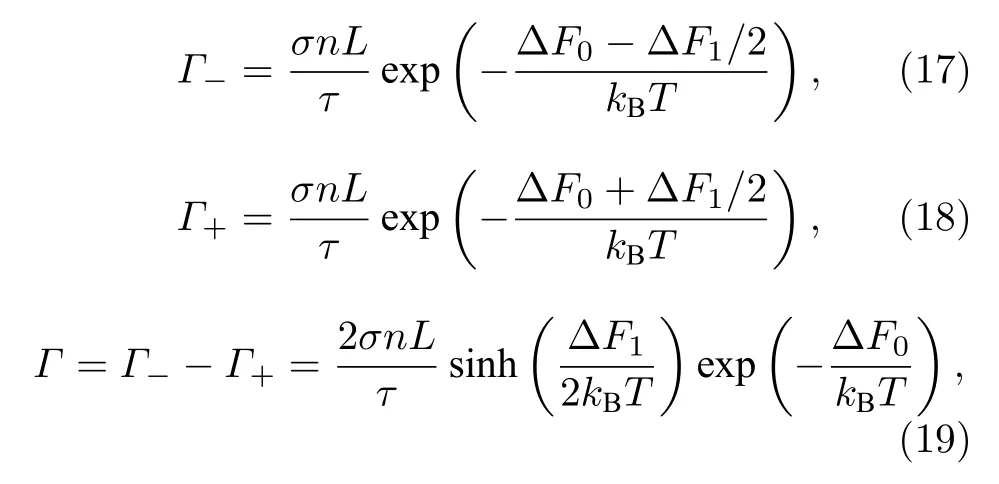
其中,σ是納米線截面,L是納米線長度,n是傳導電子數密度,因此σLn乘積表示的是整個納米線中的傳導電子數,1/τ是微觀過程的特征速率.由(14)式描述的電壓與相位之間的約瑟夫森關系可知,要使納米線上的電流保持恒定,在納米線兩端施加的電壓應該為[58]

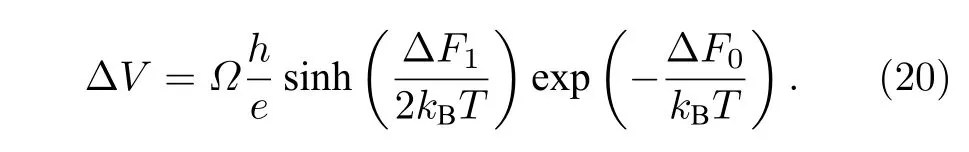
式中Ω是序參量在不同狀態間隨機散射的嘗試頻率(attempt frequency),即每秒發生TAPS 的次數.在Langer的文章中[58],Ω=σLn/τ.在小電流的極限下,sinh函數可以進行小量代換,從而得到Tc以下一維超導體TAPS 電阻的表達式為

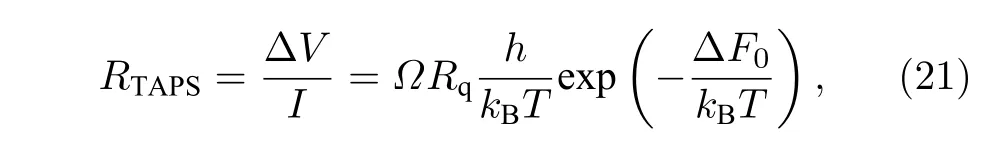
其中,Rq是量子電阻.1970 年,McCumber 和Halperin[60]計算得到更為準確的前置因子Ω 應為

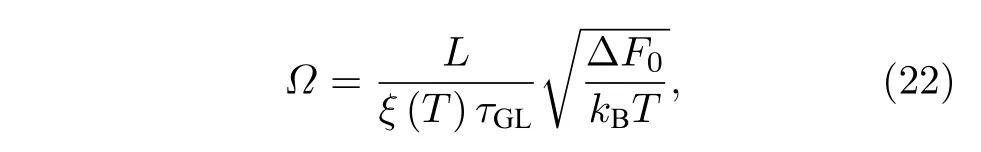
其中,ξ(T)描述了序參量變化的有效范圍,L/ξ(T)是納米線上相互獨立的相位滑移子系統數,τGL=π/[8kB(Tc–T)],即GL 時間,在每一個子系統中,序參量在特征擴散時間τGL內表現出擴散行為,因而Ω 與其倒數成正比.(?F0/(kBT))1/2是對沿納米線不同位置的重疊漲落修正,其數值接近1.(21)式和(22)式即熱激發相位滑移LAMH 理論,LAMH 模型在形式上與Little 模型一致,僅相差一些系數.由于LAMH 模型基于GL 方程,因此僅適用于Tc附近的溫區.

3.3 量子相位滑移

從經典觀點來看,相位滑移發生時,存在一定勢壘阻礙弛豫過程.單粒子通過勢壘的隧穿是量子力學的一個標志,這個概念可以擴展到超導序參量的弛豫過程.由于宏觀上成對的電子構成超導波函數,只有它們的集體行為才導致序參量隧穿,這種隧穿被稱為量子相位滑移(QPS),以區別于經典的熱激發相位滑移.QPS 可以在0 K 下發生,以至于完全耗盡超導電性.

1988 年,Giordano[61]在實驗 中發現,TAPS理論不能解釋銦納米線在低溫(T<0.5Tc)下的電阻曲線,他首次提出由于宏觀量子隧穿引起了量子相位滑移,并且使用TDGL(time-dependent Ginzburg–Landau)理論給出了相關的計算公式.Giordano 把LAMH 模型中的kBT因子替換成h/τGL,得到了一個具有啟發性的結果.

Golubev 和Zaikin 在后來的工作中給出了更為準確的微觀解釋[62?64].他們認為Giordano 模型采用了TDGL 方法,而TDGL 方法對QPS 概率的計算存在缺陷,原因如下:TDGL 理論僅在溫度接近Tc時有效,而QPS 事件可以發生在遠低于Tc的溫度下;TDGL 沒有考慮QPS 核心內準粒子產生的耗散效應;TDGL 不足以正確描述QPS事件中導線上及其周圍的電磁場.在此基礎上,Golubev 和Zaikin 提出了QPS 的微觀模型,該模型考慮了相位滑移中心內外的耗散效應.模型認為,考慮導行電磁場是很重要的,因為相位滑移不是局部的事件,它與電磁環境相互耦合,每一個相位滑移都會產生不穩定性,然后以縱向電磁波的形式,即Mooij-Schón 模[65],在納米線中傳播,這種等離子模式將能量從相位滑移中心帶走,最終以焦耳熱的形式耗散.

Zaikin 把QPS 的頻率寫為ΓQPS?exp(?SQPS),其中Ω為發生QPS 的嘗試頻率,SQPS是QPS 有效作用因子.Zaikin 認為SQPS由兩部分組成:SQPS=Score+Sout,其中Score考慮QPS 核心區域,由凝結能和正常電流耗散決定;Sout取決于電磁場在QPS 核心外的傳播.在QPS 核心外,序參量的絕對值保持一定的均值,只有序參量的相位在空間和時間上發生變化.Zaikin 計算得到Sout和Score分別為[64]:

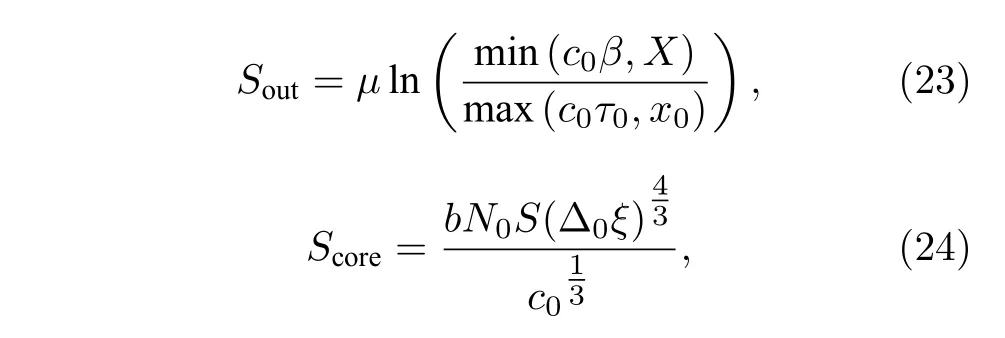
其中:τ0和x0分別是QPS 的典型持續時間和空間距離,這些參數來自于最小化Score;c0=(LkCl)1/2是Mooij-Sch?n 等離子體速度,是動態電感,λL是磁場穿透深度,Cl是納米線的單位長度電感;μ是表征一維超導體內部電磁激勵阻尼的無量綱參數;b是約等于1 的常數.為了評估SQPS,需要選擇描述相位滑移過程的試驗函數[63]:

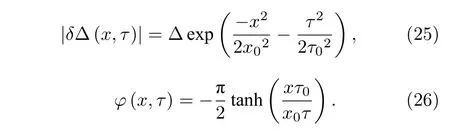
描述序參量幅值和相位的時空變化,如圖6 所示.

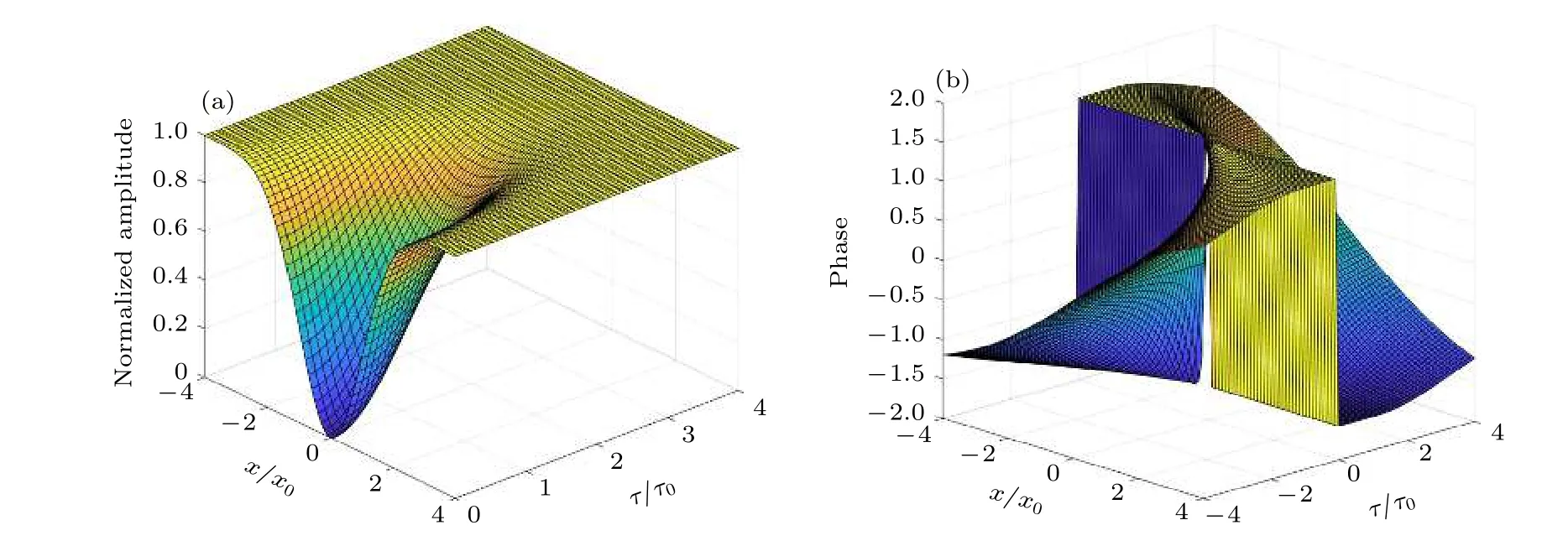
圖6 相位滑移過程的時空變化 (a)幅值變化;(b)是相位變化.在τ=0 時,序參量的幅值變為0,相位發生2π 的改變Fig.6.Temporal-spacial evolution of the phase slip:(a) Amplitute evolution;(b) phase evolution.The absolute value of the order parameter is suppressed to zero allowing the phase to flip by 2π at τ=0.

根據τ0和x0將Score最小化,Golubev 和Zaikin得到了SQPS結果如下[63]:

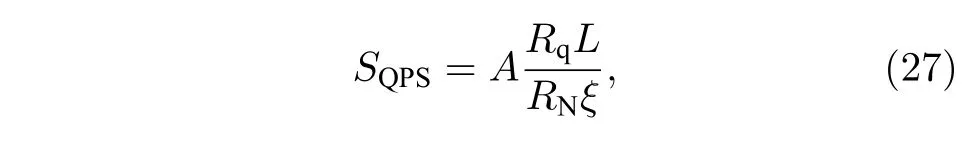
其中A是數值常數,取決于試驗函數.如果納米線的電容效應很小,即對于長度足夠短的納米線,滿足下列關系,(27)式是成立的[63]:

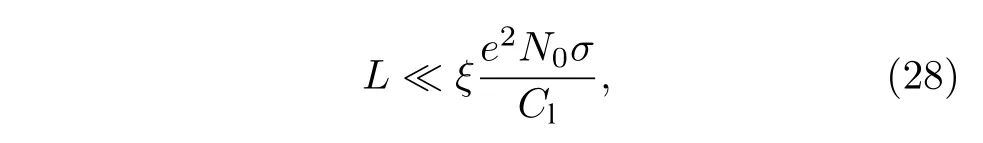
其中N0時費米面的態密度.Golubev 和Zaikin認為,對于大部分材料,只要納米線的長度低于10 μm,(28)式都成立.最終可以得到由QPS 引起的電阻值RQPS為

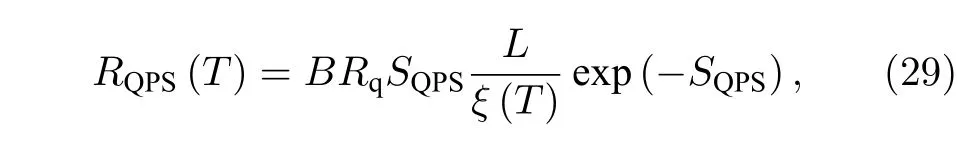
其中,A,B均為擬合常數,L為納米線長.

至此,關于相位滑移的TAPS 和QPS 已經基本形成,TAPS 主要作 用于臨 近Tc的溫區,而QPS 作用于遠低于Tc的溫區,二者存在一定的重合區間,一般來說,0.7Tc是二者的分界線.上述理論基本能解釋絕大多數的相位滑移現象,后人在此基礎上,又進一步提出了新的理論,基本上是對這些理論的的補充.

3.4 相干量子相位滑移

相干量子相位滑移(coherent quantum phase slip,CQPS)是超導現象發現以來的一個預言現象,是宏觀量子隧穿的有力例證,主要發生于一維超導體中,即厚度和寬度都小于超導相干長度的納米線[66].在納米線的兩端,不同數目的磁通量子對應于不同的量子態,這些量子態之間發生相干量子隧穿(coherent quantum tunneling),系統最終呈現出這些量子態的疊加態,此即CQPS 現象[67].另一方面,如果QPS 過程的強度不足以使納米線兩端出現這種不同磁通量子數對應量子態的疊加狀態,那么就會出現非相干的相位滑移過程,這種非相干相位滑移導致納米線出現耗散,產生2π 的相位突變,每一個相位滑移過程都對應著一個磁通量子從納米線的一段傳輸到另一端[67].CQPS 是約瑟夫森結的電荷-磁通對偶現象,在約瑟夫森結中,這種現象是由弱連兩側對應于不同數量的庫珀對的量子態之間的相干量子隧穿效應引起的,是電荷在超導線中相干傳輸的現象.約瑟夫森效應有助于制定電壓標準,相干量子相位滑移器件有望構建電流標準,可以達到非常高的精度,也有望應用在量子比特的制備中[68].

2004 年,Buchler 在實 驗中總結出連續的量子相位滑移事件可以是相干的[69].Mooij 等[70]于2006 年從理論上證明了,量子相位滑移和約瑟夫森結中的庫珀對隧穿是對偶的行為,會存在相干量子相位滑移現象,并且建議開展可行的實驗來驗證這個觀點.2012 年,Astafiev 等[66]在由強無序氧化銦制成的超導回路中首次觀察到CQPS 現象.CQPS 的一個特征是超導納米線直流偏置下的零電導現象,如圖7(a)所示,納米線的電流出現在轉變電壓Vc之后,這種現象類似于約瑟夫森節的庫倫阻塞效應[67].

相位滑移中心(phase slip center,PSC)與孤立的相位滑移不同,在沿著納米線方向的一個或者多個位置,超導電流周期性的達到Ic,并且以約瑟夫森頻率v=2eV/h在0 和Ic之間振蕩,導致納米線超導電性的耗散.PSC 最初在細的錫單晶RT曲線中被觀察到,隨后在錫晶須I-V曲線中也觀察到了類似的現象[71].在橫截面維度超過相干長度的納米線中,PSC 會轉變為相位滑移線(phase slip line,PCL)[72].基于Nb 納米線的研究發現:當偏置電流超過超導臨界電流時,PSC 最終會形成一個正常區域,也就是熱點,其內部溫度超過了超導臨界溫度[73],這個熱點在電流協助下持續增大,最終使納米線完全失超.

超導納米線I-V曲線中的電流分支跳變是PSC 的表現之一,I-V曲線固定斜率的線段體現的是一段恒定的電阻值,這個電阻值是量子電阻Rq的整數倍,如圖7(b)所示[67].除了在I-V曲線中,高偏置下R-T曲線中的電阻轉折突變也是PSC的表現[56].

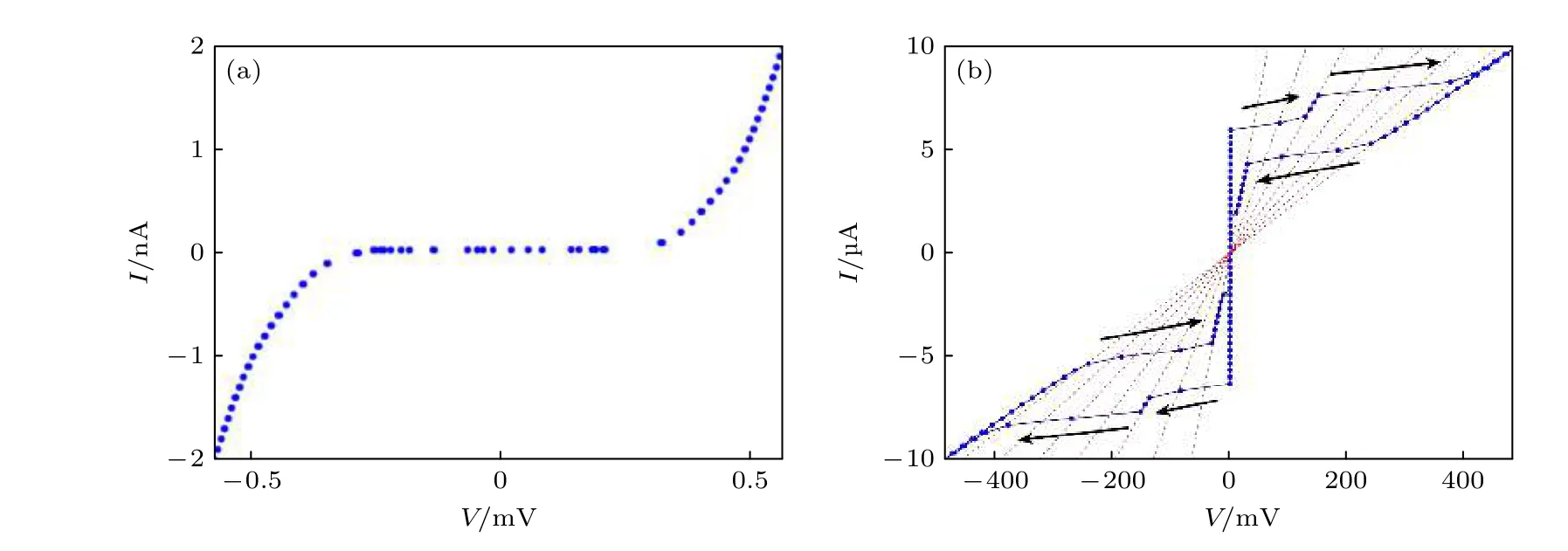
圖7 CQPS 和PSC (a)超導納米線的電流存在一個大約為300 μV 的臨界電壓,這預示著CQPS 現象[67];(b)相位滑移中心在I-V 曲線中的體現,虛線所對應的電阻值是Rq 的整數倍[67]Fig.7.The CQPS and PSC:(a) No current is measured below the critical voltage Vc ≈ 300 μV,and this behaviour is suggestive of the presence of coherent quantum phase slip[67];(b) PSC in the I-V curve of the SNSPD.The resistance corresponding to the dotted line is integral multiple of quantum resistance Rq[67].

相位滑移速率Г定義為每秒鐘發生相位滑移的次數,單位為Hz,一般反應在納米線的R-T曲線中,隨著溫度的升高和電流的增加而增大.在實驗上可以通過測量超導轉變電流Isw的分布來計算Г.在測量Isw時,即使電路做了良好的電磁屏蔽,由于相位滑移的影響,Isw也會產生一種分布,這種分布由概率密度P(I)描述[74]:

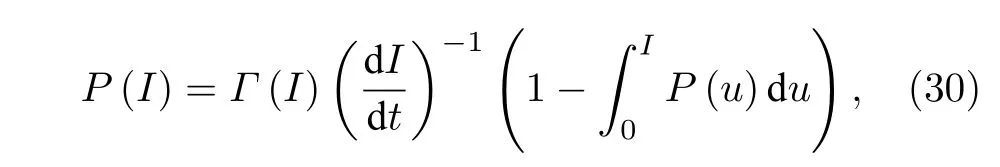
其中,Г(I)是在電流為I時發生超導轉變的速率,dI/dt是電流掃描的速率.如果單個相位滑移事件觸發超導轉變,那么超導轉變速率和相位滑移速率就是相等的.對于TAPS,Γ(I)～exp(?F(I,T)/(kBT),F(I,T)是自由能勢壘,將其與電流I線性化之后,P(I)的解服從Gumbel 分布[75].由于(30)式不存在解析解,只能由P(I)的分布推導出Г(I)的數值解[74]:

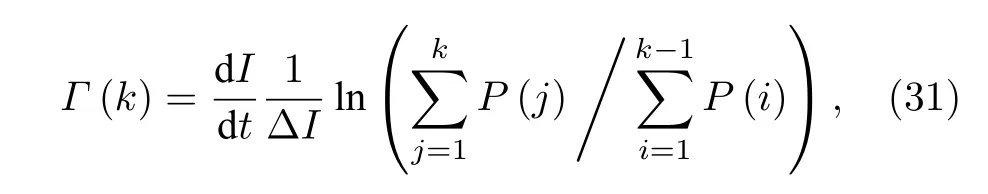
其中?I是電流掃描的間隔.實驗中經常用這種方法從Isw的分布獲得超導轉變速率Г[76],如圖8 所示[74].

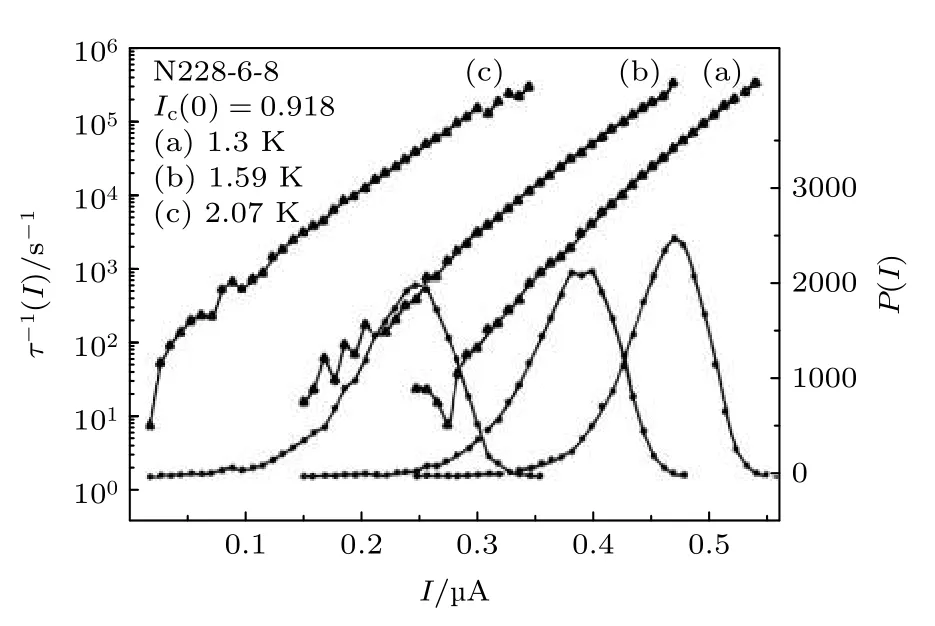
圖8 實驗中通過P(I)分布獲得Г(I)[74]Fig.8.Acquiring Г(I) by measuring the distribution of P(I)[74].

3.5 相位滑移實驗研究進展

自從相位滑移的概念提出以后,學者們對其進行了大量研究.由于在一維或者準一維的超導體中相位滑移現象較為顯著,所以實驗研究主要在超導納米線器件上進行.學者們通過使用各類超導材料(如Al,MoGe,NbN),采用不同的制備工藝(如EBL、分子模板),改變器件的幾何結構(納米線長度、寬度、厚度),施加不同的測試條件(如溫度、磁場強度)等方法,對超導器件的R-T和I-V曲線進行研究,取得了一系列的研究成果.

熱激發相位滑移目前具有公認的理論地位,自20 世紀60 年代末發展以來,它已經被用于各類實驗.為了消除實驗測量的R-T轉變由于樣品的不均勻性而導致的微小展寬,實驗上應盡可能研究非常純的樣品.第一次關于TAPS 的實驗是在自然生長的錫晶須上進行的[77,78],其典型尺寸約為0.5 mm×0.5 mm×1 mm,實驗觀察到的超導轉變過程可以用TAPS 模型來描述,測量的電阻在～1 mK 范圍內下降了5 個數量級,如圖9(a)所示.

TAPS 模型的一個顯著特點是相位滑移率與電流呈雙曲正弦關系,在早期的錫晶須實驗中驗證了這一點,如圖9(b)所示[77].實驗在低于Tc的臨近溫區測量I-V曲線,對系統的熱穩定性要求高于1 mK.

首次觀察到超導轉變偏離TAPS 行為的人是Giordano,他提出一種啟發式模型,將LAMH 模型中的kBT替換成h/τGL,來解釋In 和Pb0.9In0.1超導線的實驗數據,并將其稱為量子相位滑移,如圖9(c)所示[61].但是他的模型存在一些問題,比如:線條的均勻性如何,為什么不同橫截面的兩根導線顯示的QPS 產生的電阻有近似相同的斜率,理論上橫截面較小的導線會顯示較小的斜率,這些在他的實驗中并不明顯.

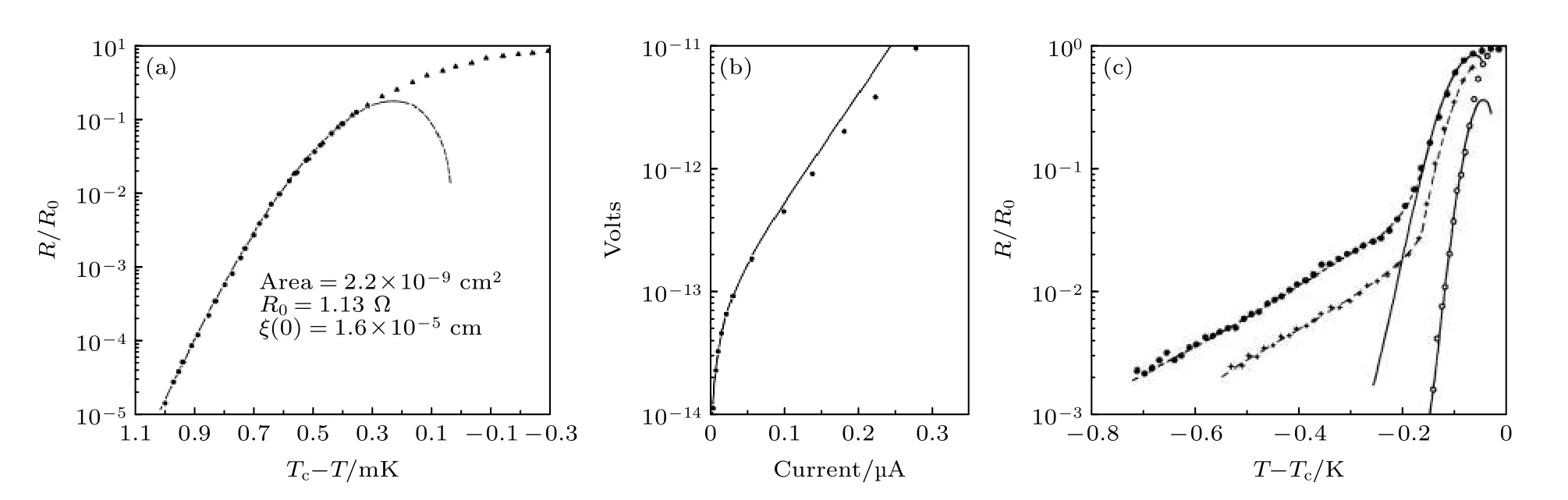
圖9 相位滑移早期實驗 (a)Lukens 等[77]在錫晶須上測量的R-T 數據,虛線是根據TAPS 公式擬合的結果;(b)在臨近Tc 的溫度測量超導線的I-V 曲線,呈現出雙曲正弦關系[77];(c)Giordano[61]首次觀察到In 超導線的R-T 曲線偏離TAPS 的行為,并稱之為QPS 現象Fig.9.Early experiments on phase slip:(a) R-T measurement of the tin whisker,and the dotted line is the result of TAPS fitting[77];(b) current-voltage characteristics at fixed temperature.Solid line,V=sinhI/2I1;closed circles,data points[77];(c) Giordano[61] observed the R-T curve of In nanowire diviated from the TAPS theory for the first time and named this phenomenon quantum phase slip.

在Giordano 的實驗基礎之上,Tinkham 等[79,80]通過實驗證明,QPS 是導致Tc以下納米線出現有限電阻的原因.Giordano 使用分子模板法,將碳納米管用作制備納米線的模板,懸浮于Si/Si0 x/SiN襯底上,再將Mo0.79Ge0.21沉積在碳納米管上,最終制備成了MoGe 納米線.Giordano 認為,納米線在低溫下是否超導,取決于它們的正常態電阻RN與量子電阻Rq的比值.若RNRq,低溫下QPS 激增,破壞了納米線的長程超導性,納米線表現為電阻態.后來Giordano 進一步修正說法,即納米線的單位長度電阻等效于納米線的面電阻,該電阻決定了納米線在低溫時的超導狀態[80].

2008 年,Elmurodov 等[81]制備了長度不同的NbN 納米線,研究不同長度納米線的相位滑移現象,結果表明,越長的納米線,發生相位滑移的頻率越高,如圖10(a)所示.雖然實驗用的納米線在3 個維度上都大于超導相干長度,但是仍然觀察到了相位滑移現象,實驗結果和TDGL 理論相符合,同時考慮了熱傳導效應.

Li 等[75]于2011 年研究了鋁納米線中相位滑移的現象.Li 制備了不同尺寸的納米線,在不同溫度下測量其Ic的均值和標準差,實驗結果分布在3 個不同的溫區.溫度低于0.3Tc時,Ic標準差與溫度變化無關,呈飽和趨勢,此時主要是QPS;溫度處于0.3—0.6Tc之間時,Ic標準差與溫度呈正相關關系,此時主要為單TAPS;當溫度高于0.6Tc之后,標準差迅速降為0,這是由于多TAPS 現象的產生,如圖10(b)所示.

2016 年,Zhao 等[82]制備了不同厚度的Nb 納米線,納米線長6 mm,寬520 nm,在低偏置電流和高偏置電流下分別研究了Nb 納米線的QPS 性能.結果顯示,納米線橫截面越小,其Tc越低,超導轉變越寬,越容易出現QPS 現象.在較低偏置電流下(5 nA),出現了典型的QPS 現象,可以用經典的理論解釋;在較高偏置電流下(100 nA),出現了新的現象:隨著外加磁場和偏置電流的改變,R-T曲線開始分離,分離的電阻值呈現出固定的5—8 kΩ,如圖10(c)所示.Zhao 認為這種情況下,在長Nb 納米線中出現了一部分的相位滑移中心,這些PSC 呈現出電阻態,電阻大小即為5—8 kΩ,其長度大約為30—48 μm,而其他大部分長度的納米線,仍然表現為超導態.

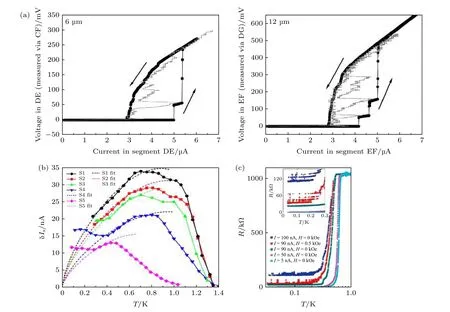
圖10 近期相位滑移實驗進展 (a)隨著納米線長度的增加,相位滑移的頻率同時增加,黑色線是電流源偏置,灰色是電壓源偏置[81];(b)鋁納米線Ic 的標準差隨溫度變化明顯分為3 個區域,分別對應于QPS、單TAPS 和多TAPS 過程[75];(c)隨著外加磁場和電流的改變,Nb 納米線的R-T 曲線出現了分離的電阻值,可能是納米線的一部分區域產生了相位滑移中心,而其他區域仍然保持為超導態[82]Fig.10.Current experiments on phase slip:(a) The phase slip rate increases with the increase of length of the nanowire.Black line:current source mode,grey line,voltage source mode[81];(b) the standard deviation of the Ic of the Al nanowire is distributed into three distinct temperature zones,corresponding to QPS,single TAPS and multi-TAPS,respectively[75];(c) the R-T curves of the Nb nanowire are splitted into different resistance with the change of the current and magnetic field,which may be caused by the phase slip centers emerging in some area of the nanowire[82].

3.6 相位滑移與SNSPD 光子檢測機制的聯系

目前越來越多的學者認為相位滑移和SNSPD的光子響應存在關聯.2012 年,Delacour 等[56]使用NbN 薄膜制備了厚度為4 nm、寬度為100 nm的納米線,在實驗中觀察到了其TAPS 和QPS 的現象,用相關公式對結果進行擬合,展示了二者的疊加狀態.實驗測量了I-V曲線和外加垂直磁場的R-T曲線,都表明了PSC 的存在.Delacour 將相位滑移現象擴展到SNSPD 光子響應中,發現隨電流增加,光響應電壓幅值出現先指數上升、再截斷的現象,并證明了SNSPD 響應的光譜依賴性在低溫下減弱.2017 年,Zhang 等[83]研究發現SNSPD的超導轉變電流和阻抗匹配存在關聯,并推測阻抗匹配電路實現超導轉變電流最大的原因可能是:電路容易釋放由于相位滑移形成的臨時電阻態.

Lyatti 等認為,存在一個熱點電流IHS=Ic–jcEph/[nsΔ(πDtth)0.5],只有當偏置電流大于IHS時,光子吸收后才會形成一個局部的熱點,繼而在電流的加熱作用下,熱點阻斷整根納米線,納米線變為正常態.式中D是準粒子擴散系數,tth是準粒子熱化時間,Δ是超導能隙[84].當偏置電流小于IHS時,納米線吸收光子會降低納米線的超導性能,但是不會產生熱點.Madan 等[85]認為,當I>IHS,光子吸收使納米線產生熱點,導致序參量在熱點區域局部坍縮.納米線從這個瞬態演化到一個具有相滑移過程的狀態,導致納米線從超導狀態轉變到電阻狀態.

2020 年,Lyatti 等[84]制備了YBCO 納米線,對其超導轉變電流Isw進行了研究,發現在溫度高于和低于交疊溫區Tcr時,Isw呈現單峰分布;當溫度等于Tcr時,Isw呈現多峰分布.他們認為,溫度高于Tcr時,相位滑移主要由TAPS 引發,溫度低于Tcr時,相位滑移主要由QPS 引發;而處在交疊溫區時,由于納米線存在分離的能級,導致相位滑移具有多重隧穿途徑,因此Isw的分布呈現為多峰狀態,如圖11 所示.隨后,Lyatti 在針對光響應的研究中,也發現了相應的能級分離現象.Lyatti 認為,由于納米線吸收光子,序參量發生局部坍縮,出現振蕩相位滑移過程,納米線進入電阻狀態.光子吸收改變了納米線中相滑移過程的數目,即納米線的相滑移狀態,他們稱之為光子探測的相滑移機制.

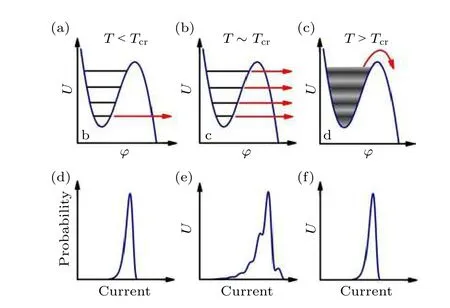
圖11 YBCO 納米線中能級量子化現象,并提出了SNSPD光子探測的相位滑移解釋[84]Fig.11.Energy level quantification in the YBCO nanowire,and the phase-slip based photon detection mechanism of SNSPD is proposed[84].

4 總結與展望

目前還不存在一種理論能解釋所有SNSPD檢測機理實驗中觀察到的現象.在探究光子響應機制時,一種常用的方法是固定入射光子波長和入射光子數,改變偏置電流Ib,測量光子計數率和Ib之間的關系.隨著Ib增加,光子計數率曲線一般是先指數上升再達到飽和,我們把計數率達到飽和的偏置電流值稱為Ith(threshold-current),Ith是研究光子探測模型時常用的參數.擴散熱點模型的缺陷是不能解釋光子探測時Ith的位置依賴(position dependence)現象,即對于固定能量的入射光子,Ith依賴于光子在納米線截面上的吸收位置[86],Renema 等[87]進行的偏振測量實驗證實了這種現象.正常核渦旋模型(normal-core vortex-model)是所有模型中最基本的模型,該模型假設由于快速衰減的序參量,準粒子被限制在熱點以內,可以使用一個非均衡方程描述準粒子的分布.當光子吸收位置足夠靠近納米線的邊緣時,該模型的解可以用來描述單渦旋穿越納米線的情形;當光子的吸收位置靠近納米線中心時,該模型預測渦旋-反渦旋對在熱點中形成,偏置電流足夠高時,渦旋對被拆散,渦旋朝著相反的方向往納米線邊緣運動,從而引發正常態.這個模型能很好地描述實驗中獲取的光子能量-偏置電流關系,以及磁場環境下的光子計數率,然而也不能解釋光子探測時Ith的位置依賴現象.基于準粒子擴散的渦旋穿越模型(diffusionbased vortex-entry model)預測了線性的光子能量-偏置電流關系,這與實驗結果吻合得很好[35],同時這個模型也很好地再現了Ith的位置依賴關系.然而,當光子吸收位置太靠近納米線邊界處時,由于納米線的超導鄰近效應,即由于納米線制備時的缺陷、氧化等原因造成納米線邊緣變成正常態,該模型的預測會產生系統性誤差.此外,基于相位滑移的SNSPD 光子檢測理論目前還處于發展階段,尚未形成統一的理論.

目前,SNSPD 檢測機理的研究還面臨一系列具有挑戰性的問題,這些問題的解決能使SNSPD的發展取得重大突破.其一,確定從光子吸收到產生正常電阻態區域的時間差,即明確影響時間抖動的微觀過程.光子入射后伴隨著庫珀對拆散、準粒子擴散、電子-聲子散射等復雜物理過程,擴散熱點模型和正常核渦旋模型原則上能回答時間抖動的本質問題,但都需要進一步精確描述準粒子擴增和熱點形成的過程.一般來說,從光子吸收到產生正常電阻態的時間差約為幾皮秒,使用光子吸收位置分布的統計學分析可以得到SNSPD 的極限時間抖動.

其二,闡明暗計數形成的機理,即明確SNSPD噪聲的本質起因.暗計數是指在沒有光子入射時SNSPD 產生的電壓脈沖,決定了SNSPD 的噪聲等效功率.暗計數包括背景輻射暗計數和本征暗計數,背景輻射暗計數源于黑體輻射、偏置電流的電子噪聲和外界電磁輻射等,這些可以使用合適的濾波器和電磁屏蔽方式解決.目前有多種理論解釋本征暗計數的來源,包括渦旋穿越、渦旋-反渦旋破對、超導序參量的波動、熱激發相位滑移和量子相位滑移等.闡明暗計數的形成機理一方面有助于提高SNSPD 的噪聲性能,另一方面,由于暗計數和光子響應有諸多相似之處,暗計數形成的機理研究也有助于加深我們對光子檢測機理的理解.

其三,明確渦旋對于解釋SNSPD 光子探測機理的適用條件,即探索渦旋無關的SNSPD 光子響應機理.近期對WSi 納米線SNSPD 的研究表明[88,89],這種器件可以工作于高達0.7Tc的溫度,并且探測效率在飽和區域相當平緩,這是目前其他材料不可比擬的優勢.此外,由于WSi 是非晶材料,具有低Tc和低電子態密度,在吸收中遠紅外的低能量光子后可形成較大的正常電阻態區域,這啟發我們在研究不同超導材料的SNSPD 時,探索渦旋在SNSPD 光子響應理論中的適用條件;另一方面,由于渦旋在寬度小于4.4ξ的納米線中不能形成,針對極窄線寬的SNSPD,未來有可能發展出一種無需渦旋參與的SNSPD 光子探測理論.

深入理解和厘清SNSPD 光子響應過程是SNSPD 發展的前提和基礎.SNSPD 的熱點模型、渦旋模型與相位滑移模型各有特點、各有長短,三種模型是對SNSPD 光子檢測理解的不斷深入.熱點模型啟發于物理直覺,是一種唯象模型,由熱力學出發,研究電子-聲子等準粒子體系的相互作用;渦旋模型是基于電磁學的解釋,由GL 方程和電磁學方程出發,研究渦旋在超導體中的運動及其帶來的超導態耗散;相位滑移模型是基于量子力學的解釋,由超導波函數出發,研究熱擾動和宏觀量子隧穿引發的超導態耗散.同時這三種模型又是相互聯系的:熱點的形成降低了渦旋穿越的勢壘[45,46],每一個相位滑移事件都伴隨著磁通量子從納米線的一段穿越到另一端[67],類似于渦旋穿越的過程.這三種理論的總結如表1 所示.

表1 熱點模型、渦旋模型、相位滑移模型特點總結Table 1.The summary of the hot spot model,vortex-based model and phase-slip-based model.

基于相位滑移理論的SNSPD 光子檢測模型是未來的一個重要發展方向.相位滑移模型從熱擾動和宏觀量子隧穿的角度探究納米線的光響應過程,與熱點模型、渦旋模型不存在沖突.由于相位滑移模型是建立在量子力學之上的微觀解釋,能避免熱點模型和渦旋模型的短板,未來有可能在相位滑移理論的基礎上發展出統一的SNSPD 光子檢測理論,這種理論可以解釋目前光子檢測機理實驗中發現的Ith位置依賴現象,也能解釋不同材料制備的SNSPD 在不同測試環境中所表現的光子能量-偏置電流依賴關系.下一步,我們將研究光子入射和相位滑移之間的定量關系,揭示納米線吸收光子對相位滑移事件的影響,探索發展統一的相位滑移模型.