N=Z 原子核64Ge 可能存在的三軸形變*

沈水法 王華磊 孟海燕 閻玉鵬 沈潔潔 王飛鵬 蔣海濱 包莉娜

1) (浙江廣廈建設職業技術大學智能制造學院,金華 322100)

2) (中國科學院合肥物質科學研究院核能安全技術研究所,合肥 230031)

3) (福建工程學院電子電氣與物理學院,福州 350118)

4) (中國科學院近代物理研究所高精度核譜學重點實驗室,蘭州 730000)

5) (鄭州大學物理學院,鄭州 450001)

6) (蘇拉娜里理工大學物理學院,那空叻差是瑪 30000)

7) (泰國高等教育委員會物理卓越中心(ThEP),曼谷 10400)

8) (杭州師范大學醫學部,杭州 310012)

9) (陸軍炮兵防空兵學院,合肥 230031)

為尋找核態可能存在的三軸形變,用對力-形變-轉動頻率自洽推轉殼模型對鍺和硒同位素進行了總轉動能面計算.計算是在四極形變(β2,γ)網格中進行的,且十六極形變β4 可變.在鍺同位素中發現了由64Ge 的三軸、66Ge 的扁橢、再經三軸、向長橢形變的形狀相變.一般來說Ge 和Se 同位素具有γ 軟性形狀,導致了顯著的動力學三軸效應,計算中沒有證據表明存在基態下的剛性三軸性.在64,74Ge 中發現基態和集體轉動態下γ=?30? 的三軸形變,這是三軸形變的極限.本文重點討論N=Z 核64Ge 可能存在的三軸形變,給出了基于唯象Woods-Saxon 勢下的單粒子能級信息,并對N=Z 核64Ge 三軸形變的產生機理進行了討論.

1 引言

研究表明86%的核有長橢球形狀[1],雙幻核附近有球形形狀.在缺中子汞和鉛同位素中扁橢球形變也被發現[2].核能夠非軸對稱地形變,非軸對稱形變可由核形狀的γ自由度描述.γ形變導致核的特征集體運動,例如:搖擺運動[3]、手征帶[4]、轉動帶旋稱反轉[5].毫無疑問γ軟性和科里奧利耦合是破壞系統的動力學軸對稱最重要的機制[6].有|γ|=30°的最大三軸形變的穩定三軸形狀嗎? 最近的一個研究工作用Skyrme Hartree-Fock-BCS和Gogny-Hartree-Fock-Bogoliubov(HFB)對核基態的計算,預言了大部分鍺同位素有軟三軸形變[7].本工作中,我們使用推轉Woods-Saxon 殼模型來研究可能的三軸形狀,包括形變激發態.對于描述三軸形狀的核,有一個長期存在的問題,即這些核是硬的還是軟的γ形變,參見文獻[8?10]中的討論.在一些計算[7,11,12]和數據[11]中建議64Ge 基態為三軸的.根據Ennis 等[11]的平均場近似理論計算,N=Z=32 核64Ge 是N=Z豐質子不穩定核中顯示γ-軟性結構的典型例子,計算預測了基態可能的γ不穩定性和激發態的三軸性,即四極形變β2～0.22 和γ～27°,而Yamagami 等[12]用Skyrme-HFB 方程作數值計算得到對64Ge 的解為β=0.27、γ=25°和β3=0.Ennis 等[11]的研究 還顯示64Ge 核是反射不對稱和三軸自由度之間強耦合的唯一候選核.他們的結果與Skalski 的研究[13]是一致的,后者使用了相當豐富的涉及β3和γ的核形狀參數,并證實了對這個奇異N=Z系統八極不穩定性和γ-軟性的預測.通過Skyrme Hartree-Fock 自洽計算也得到了類似的結果[14].Kaneko 等[15]基于球形殼模型基研究了N=Z核64Ge 中的四極關聯和八極關聯,他們用配對加四極加八極相互作用帶有單極修正進行了殼模型計算,結果表明64Ge 對于無論是四極形變還是八極形變都是不穩定核,這與先前預測γ軟性和八極不穩定性的討論是一致的.本工作我們試圖從新的視角即用對力-形變-轉動頻率自洽推轉殼模型著重討論64Ge的三軸形變.

2 模 型

在核素圖大范圍內偶 -偶核的非軸對稱由Andrejtsche 等[16]使用求和規則進行了研究,其采用一個近似.它給出核在低位態時三軸形變的可能性[17,18].為完整起見重寫該方法的主要公式如下[16]:

這里在推導等式(1)時使用了近似,δeff值(至較高級項)對應于集體模型非對稱角γ[16,19].(1)式的有效性為核素圖大范圍內偶 -偶核非軸對稱形狀參數δeff的提取和系統性研究提供了方便.用這種方法,根 據(1)式對 4 6 ≤A≤82(22 ≤Z≤34)[16]和94 ≤A≤192(42 ≤Z≤76)[19]質量區的近70 個偶-偶核基態的 〈 cos 3δ〉期望值進行估計,這近70 個核其E2 矩陣元的數據是可獲得的,然后這些核基態非軸對稱形狀參量δeff(對應于Bohr 模型參量γ)根據(2)式得到.文獻[16]表明對所研究的核在非軸對稱性和四極形變之間存在一種整體關聯,而且發現72–76Ge 和74–78Se 的基態有非常顯著的(有效的)三軸形變.最大三軸形變在基態是非常罕見的,常見的是發生在高自旋態.過去主要是對高自旋態對于軸對稱的可能偏離開展過廣泛的討論(參見文獻[20]及其參考文獻).(1)式給出非軸對稱參量的平均值δeff,但它沒有提供γ自由度方向上核形變軟度的信息.應該強調的是基于(1)式中矩陣元的三階項的分析,無法確定三軸形變是軟性的(動態的)還是剛性的(靜態的)[16].δ的軟度由實驗E2 矩陣元的六階項決定,它目前只在非常少的核中獲得[17].有幾個工作提示非軸對稱一般是動態的,即牢固地建立起剛性三軸形變的核幾乎不存在(參見文獻[21,22]及其參考文獻).

在本文中我們集中研究三軸形變包括三軸參量γ的軟度.用對力-形變-轉動頻率自洽推轉殼模型來作總轉動能面(total Routhian surface,TRS)計算[23,24].在TRS 計算中,單粒子能量由非軸對稱形變的Woods-Saxon (WS)勢獲得[25,26],計算過程中使用的WS 勢參數[27,28]為:a)半徑參數:r0(p)=r0(n)=r0-so(p)=r0-so(n)=1.190 fm;b)中心勢阱參數:V0=53.754 MeV,k=0.791;c)自旋軌道耦合強度參數:λ(p)=λ(n)=29.494;d)表面彌散參數:a0(p)=a0(n)=a0-so(p)=a0-so(n)=0.637 fm.其對關聯由Lipkin-Nogami (LN)方法處理得到[29,30].單極對力強度參量G由平均能隙方法決定[31],在本工作中質子和中子的單極對力強度Gp和Gn分別為0.292 MeV 和0.303 MeV.總能量包括從標準液滴模型得到的宏觀部分[32]和從Strutinsky 殼修正得到的微觀部分[33,34].計算在四極形變 (β2,γ) 的 網格中進行,且十六極形變 (β4) 可變.對一個給定的轉動頻率ω,對關聯在任何給定形變格點上由解推轉LN 方程自洽處理(即前面提到的對力-形變-轉動頻率自洽處理),然后形變由得到的TRS 取最小值來確定(其細節參見文獻[23,24]).已包括在雙拉伸坐標空間中的四極對力[35,36],其對能量的影響可忽略,但是對集體角動量卻有重要影響[24].

3 計算和討論

對偶質量核64-80Ge 基態從總轉動能面(total Routhian surface,TRS)計算得出的形變顯示在圖1 中.在該計算中,在四極形變 (β2,γ) 的各個網格點,總羅斯量對十六極形變β4取最小.軸對稱長橢球(扁橢球)形狀對應于γ=0°和γ=–120°(± 60°),而其中的γ=60°和γ=–120°為非集體轉動(可以是粒子-空穴激發).根據文獻[37]的定義,形變軟度從TRS 計算得到,由圖1 中的誤差棒所示.對鍺同位素基態,我們看到從64Ge 的三軸形變到66Ge 的大形變的扁橢球,通過74Ge 的γ=–30°三軸形狀到78,80Ge 的微弱形變的長橢球的形狀變化(基態TRS 對γ=0°和–60°是反射對稱的),這和由Lecomte 等[38]確定的N=40 附近可能存在的形狀轉變相符.應該指出,核基態具有扁橢球形狀是罕見的[39,40],在穩定核基態中出現γ=30°的三軸形狀幾乎是唯一的.

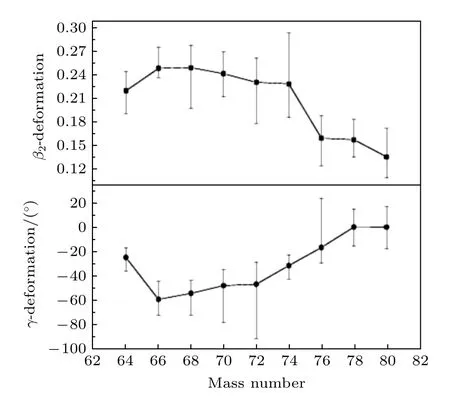
圖1 總轉動能面計算得出的偶質量核64-80Ge 的基態形變.誤差棒顯示對應于能量高出最小值100 keV 以內的形變值,此表示各個核對應于相應形變參數(β2 和 γ)的軟度Fig.1.Deformation obtained from total Routhian surfaces for ground states in even-mass 64-80Ge.The error bars display the deformation values within an energy range of less than 100 keV above the minimum,giving an indication of the softness of the nucleus with respect to the corresponding shape parameter(β2 and γ).

在目前工作中,為了研究64Ge 三軸形變的穩定性,對該核的正宇稱轉暈態作TRS 計算.圖2中給出在特定轉動頻率ω=0.0,0.4,0.7,0.9 MeV下的總轉動能面,對應于自旋范圍I～(0?16).根據對正宇稱轉暈態總轉動能面(TRS)的計算,在=0.0 MeV 時(即原子核不發生轉動,對應于原子核處于基態,此時I0 ),極小點處于β20.224、γ?94.9?,因基態(此時原子核還沒有轉動)TRS 對γ=0°和–60°是反射對稱的,所以γ?94.9?等價于γ?25.1?、也等價于γ25.1?,是為三軸形變的核,但此時核64Ge 被預言沿γ方向有點軟.隨著轉動頻率增加到=0.4 MeV,極小值變到β20.250、γ?39.4?(因為比較軟,所以可以認為變化不大)并且勢阱變得深一些(因而變得較硬一些).這第一個極小值在轉動頻率1.0 MeV 處消失.另一方 面,在轉動 頻率為0.7 MeV 時(對應于圖2 的左下部分),第二個極小值出現,并且在轉動頻率0.8 MeV 時成為最小值,其為較大形變β20.360 和γ4.0?,即長橢球形狀.隨著轉動頻率的進一步增加,這個最小值的γ形變變到 6 0?,即為非集體轉動的扁橢球.

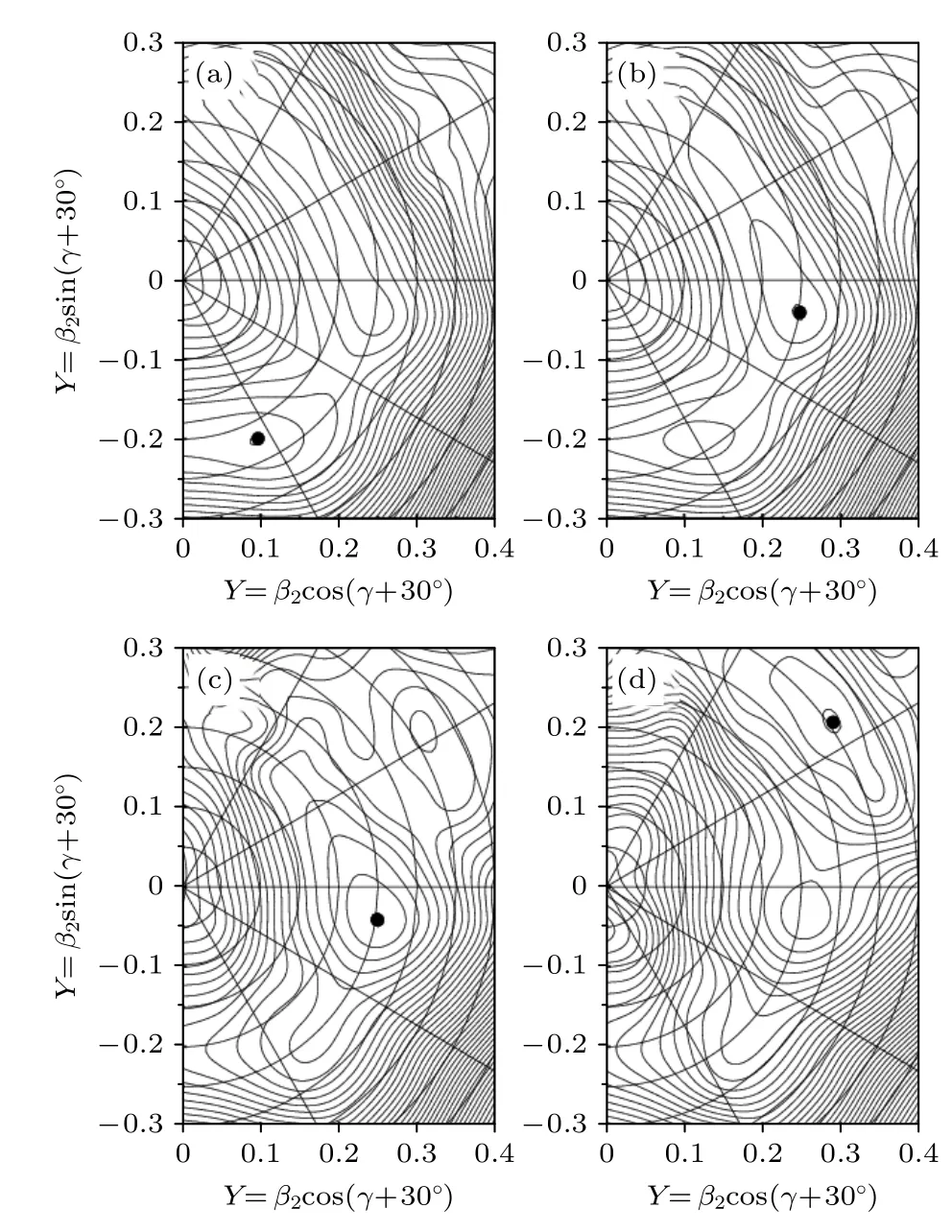
圖2 對64Ge 的正宇稱轉暈態在給定轉動頻率 (a)=0.0 MeV,(b) =0.4 MeV,(c) =0.7 MeV 和(d) =0.9 MeV 下計算得到的總轉動能面,其對應于自旋 I ～(0?16).圖中黑點表示最小值,相鄰等位線的間隔是200 keVFig.2.Calculated TRS's for 64Ge positive-parity yrast states at (a) =0.0 MeV,(b) 0.4 MeV,(c) 0.7 MeV,and(d) 0.9 MeV corresponding to I ～(0 ?16).The black dot indicates the lowest minimum,and the energy difference between neighboring contours is 200 keV.

為了了解三軸形變的起源,我們計算了對應于三軸形變參數γ的Woods ? Saxon 勢單粒子能級圖,見圖3.

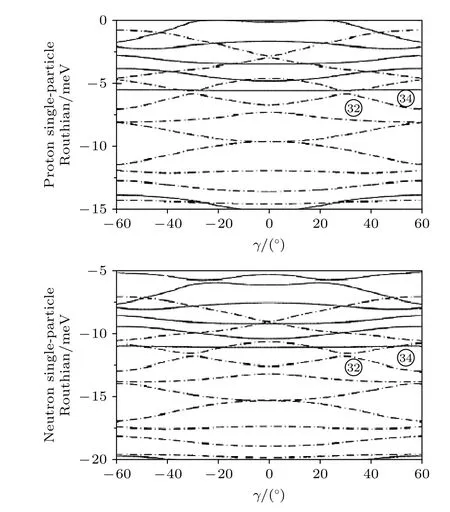
圖3 對應于三軸形變參數γ 的Woods-Saxon 勢單粒子能級圖Fig.3.The calculated Woods-Saxon single-particle levels versus the triaxial deformation γ.

圖3 是取 (Z,N)(32,38) 在形變 (β2,β4)(0.24,0) 下作的計算.這些參量代表了這里所研究的大形變核的一般性質.我們看到,在Z=32和N=32 處有一形變的γ30?殼能隙.TRS 計算顯示,核64Ge 有一不太軟的三軸形狀γ≈?25?(參見圖1).但是,在N=34 處出現一個扁橢球殼能隙,其結果導致在66Ge 中的扁橢球形狀.隨著中子數的增加,扁橢球中子能隙的效應減小,因此更重的鍺同位素的形變向三軸(或長橢球)形狀變化.上面已經提到Andrejtsche 等[16]發現72-76Ge 和74-78Se的基態有非常顯著的(有效的)三軸形變,為了確定這些核的三軸形變是軟性的(動態的)還是剛性的(靜態的),我們在對力-形變-轉動頻率自洽推轉殼模型框架下對其中的74Ge 和74Se 核進行了討論,圖4(a)和圖4(b)分別是總轉動能面計算得到的74Ge 和74Se 的運動學轉動慣量(也稱第一類轉動慣量)J(1)及對應的從實驗測到的能級能量提取出的運動學轉動慣量,從中可以看出理論計算值與實驗值存在差異,總轉動能面計算基于推轉殼模型,其只考慮轉動,沒有考慮振動,理論計算值與實驗值的明顯差異說明74Ge 和74Se 有振動行為,對64Ge 比較理論與實驗值,發現也是如此.這與上面提到的“非軸對稱一般是動態的,即牢固地建立剛性三軸形變的核幾乎不存在(參見文獻[21,22]及其參考文獻)”相符.所以需要提及的是目前TRS計算不能合理地再現觀測到的激發態實驗數據,實驗數據[41,42]顯示強烈的振動效應,該效應未能包括在TRS 模型中.另一方面,現在的模型作一維主軸推轉,對三軸形狀,原則上應該作三軸推轉.但是,一維推轉模型應該能給出關于形變的一個正確描述.作為在各種質量區分析原子核基態和激發態形狀的方法,TRS 在研究三軸形變方面扮演著重要的角色,尤其是研究具有軟性的三軸形變.

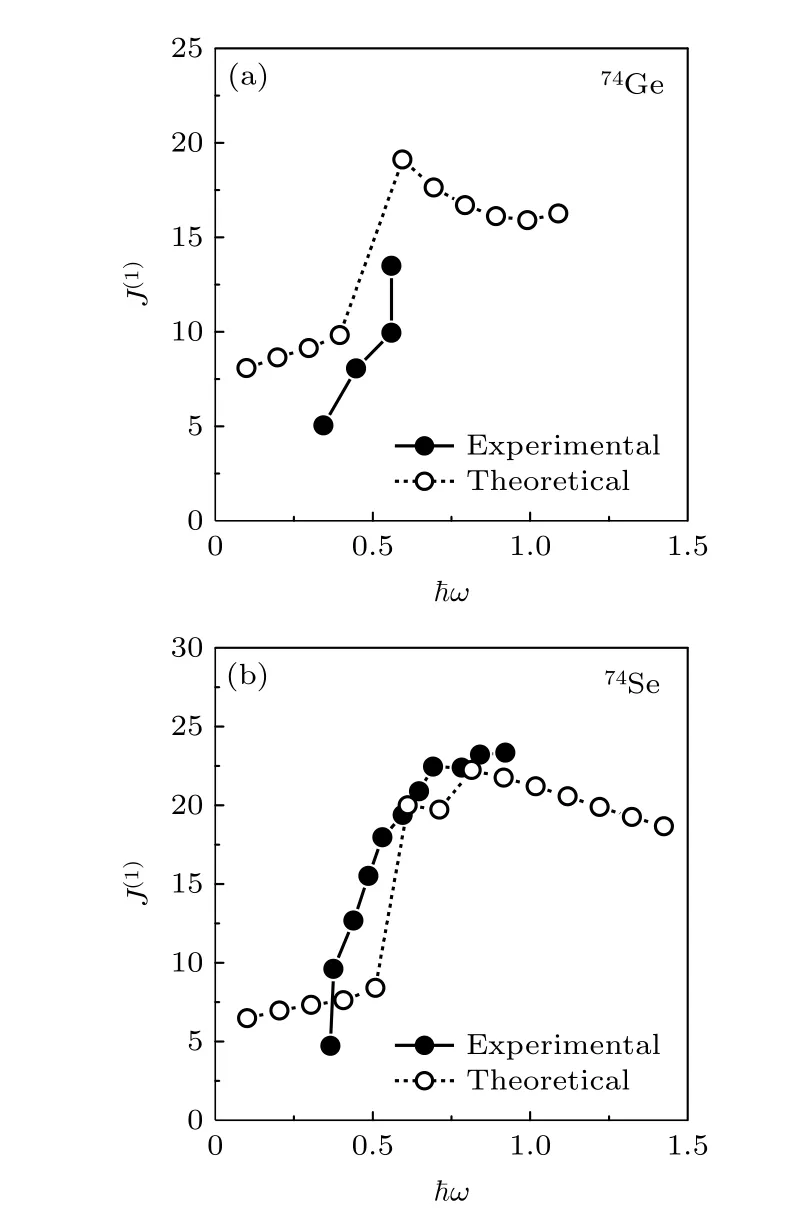
圖4 對(a) 74Ge 和(b) 74Se 核由TRS 計算得到的運動學轉動慣量J(1)與由實驗結果提取出的比較Fig.4.The kinematic moment of inertia J(1) calculated by TRS is compared with those extracted from the experimental results for (a) 74Ge and (b) 74Se.

4 結論

在現在的工作中,作為例子,使用推轉Woods-Saxon 殼模型對64-80Ge 同位素的正宇稱態作自洽形狀計算,即對力是形變和轉動頻率依賴的,用來討論形狀相變,特別是從基態開始的強的非軸對稱.在我們的TRS 計算中,Ge 同位素形狀顯示出有γ軟性的三軸形變,而64,74Ge 顯示最顯著的三軸形變.基于唯象Woods-Saxon 勢下的單粒子能級,對N=Z核64Ge 三軸形變的產生機理進行了探討.本文工作給出對這些核的一個進一步理論理解,證明了為了得到一個關于形狀硬度清楚的圖像,正像本文所顯示的在β2-γ坐標平面上計算它們的總轉動能面(TRS)總是有用的.可以看出取近似后的總和規則方法為量度關于振動或γ軟核的有效的三軸形變提供了一個有效的方法[16],對剛性轉子,γeff是與幾何γ值相等的[43].而我們用對力-形變-轉動頻率自洽推轉殼模型來作總轉動能面計算,可確定核形狀和它的軟度,不僅對基態還是對激發態,本文的工作是特別適當的.