基于Bayes估計的民航維修人為差錯評估技術探究

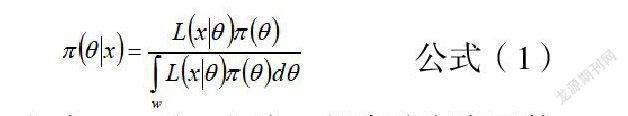
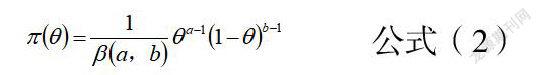
摘要：本文將基于Bayes（貝葉斯）評估方法入手，在了解該算法的基本原理之后介紹了各種人為差錯的數據來源;再闡述了貝葉斯技術在民航維修人為差錯評估中的應用方法，并結合應用實例進一步介紹了該評估方法的使用效果，希望為降低誤差發生率提供支持。

關鍵詞：Bayes;民航維修;人為差錯

前言：人為差錯是指工作人員出現與質量標準、工作目標相偏離的行為。在民航維修中，人為差錯不可能完全杜絕，但是考慮到飛行器屬于高精尖設備，任何誤差的出現都有可能造成嚴重后果，所以必須要對民航維修的認為差錯問題展開分析，Bayes技術的出現有效解決該問題，值得關注。

1.Bayes的基本原理以及人為誤差的來源

1.1Bayes基本原理

貝葉斯評估是目前學術界一種先進的評估手段，該方法主要在設定待估算參數的“先驗分布”之后，該先驗分布可以由工作人員的經驗以及歷史采集的數據來確定，根據先驗分布結果以及相關數據計算出后驗分布情況，而利用后驗分布則可以對各種可能出現的未知現象展開評估。與傳統的誤差評估方法相比，貝葉斯不僅能夠涵蓋各類樣本信息，也能對先驗信息進行挖掘、分析的基礎上，使原本復雜的信息量化，通過拓展數據的分布范疇來保證先驗分布效果，所以最終的評估質量能夠得到保障。貝葉斯推理的問題是條件概率推理問題，這一領域的探討對揭示人們對概率信息的認知加工過程與規律、指導人們進行有效的學習和判斷決策都具有十分重要的理論意義和實踐意義。

在本次研究中，本文假設帶估計的民航維修人為差錯概率為θ，在連續分布的隨機變量下，貝葉斯的計算方法如公式（1）所示。

在公式（1）中，π（θ）為θ的先驗密度函數;π（θ|x）代表θ在x條件下的條件密度函數;w為參數空間;L（x|θ）為樣本似然函數，在人為維修差錯概率給定的情況下發生失效的分布情況;π（θ|x）代表后驗分布的密度函數。

在運用貝葉斯評估方法期間，其中需要先針對每個信息源構造前分布方案，在對隨機數據標量進行估計的基礎上，確定信息源后;一般在計算人為誤差期間，假設整個維修過程中存在n個信息源，在每個信息源賦值均為可讀取的情況下，并統計其中的驗算結果。

1.2人為差錯的數據來源

1.2.1通用數據

通用數據體現了評價行為形成因子情況，要求在差錯分析中能針對行為形成因子來對各類人為差錯概率進行標定。在貝葉斯算法下，通過整合現場人為誤差以及通用數據后，當現場數據數量較少時，則要避免現場數據被淹沒，所以針對這種情況，通過在貝葉斯算法中開展關于認知可靠性與差錯的分析能夠提供人為差錯數據以及任務場景，這也是貝葉斯需要重點實現的內容。

1.2.2仿真技術

考慮到民航維修工作的復雜性，為了能夠最大限度上提高誤差控制能力，相關學者開始運用計算機仿真技術對人為差錯進行控制，但是因為仿真技術的精準度無法得到保證，因此在數據仿真過程中容易造成誤差。

2.貝葉斯算法的應用流程

2.1確定先驗分布

在計算先驗分布期間，主要是利用估算方法來計算出人為差錯的分布情況，其中的關鍵技術步驟包括：

步驟一：通過設定分布族為先驗分布族，期間假設民航維修的次數為n次，其中發生差錯的次數為f次，此時維修的認為差錯概率滿足二項分布的要求。針對這種情況，按照貝葉斯算法可先在（0，1）的區間內均勻分布先驗數據，在確定其滿足先驗分布的基礎上，共軛先驗分布族可以按照Beta的算法分布，此時基于Beta的函數分布模式可以按照公式（2）進行驗算。

???? 公式（2）

在公式（2）中，a與b分別代表Beta的分布參數情況;代表Beta函數。

步驟二：相關學者認為維修過程中人為誤差的發生率為5%[1]，在本次研究中采用5%為差錯的中值。在這種情況下，按照貝葉斯先驗分布類型，驗算估算法確定通用數據的先驗分布情況。為了實現這一目標，可按照公式（3）展開運算。

2.2貝葉斯先驗分布參數的計算

考慮到民航維修差錯的先驗信息來源復雜，在對各種人為差錯數據展開分析后，結合統籌數據計算人為差錯發生率。在這種情況下，因為上數據本身就有樣本特征，在海量數據處理過程中可借助仿真模

型來判斷各個數據之間通用性，在假設的情況下，假設分布參

數a與b的仿真模型如公式（4）所示。

在開展貝葉斯先驗分布參數計算中，在公式（4）的求導過程中，通過確定一個使達到最大的極值即可。

2.3確定后驗分布

在后驗分布中可以按照貝葉斯定義，按照樣本偶然系數，并根據Beta分布方法，使以及后，選擇Beta的分布中間值進行貝葉斯估算，則估算結果如公式（5）所示。

3.實例分析

3.1民航維修人為誤差的項目背景介紹

某民航公司的維修任務達到150次/月，維修工作中會因為操作不規范而導致維修質量問題。根據公司提供的維修記錄，截至2020年，因為技術原因所造成的維修差錯概率均值為3.1×10，根據這組數據計算出Beta分布函數的分別為：a'=2.845、b'=628.03，在將數據代入到公式中之后，計算出貝葉斯θ=4.45×10，按照這一數據可以認為案例民航維修人員在維修期間，因為技術問題而造成的差錯概率為4.45×10。在這種情況下，假設不使用先驗信息，單純采用傳統的最大似然估計法，選擇相同的數據展開計算后，則計算出失效概率為8.0×10，由此可見，貝葉斯定義方法能夠進一步降低失效概率發生率。

2.2利用現場數據進行檢驗

針對民航公司的實際維修部記錄，統計該公司因為技術問題而造成的維修誤差概率均值達到了6.3×10，在將運算數據與實驗結果展開對比后，根據現場數據以及貝葉斯的估算結果，證明兩個數據在內容上十分接近，這一結果證明了該方法在評估民航維修人為誤差管理中發揮著重要作用。

結束語：

在估算民航維修人為差錯結果中，采用貝葉斯估算方法具有可行性，該方法的計算結果與現場驗算結果基本相同，該方法因為能夠進一步計算出維修人員的工作誤差問題，對于整個民航維修工作開展具有影響。因此相關人員需要深入了解貝葉斯估算的技術要點，爭取為更好的控制誤差奠定基礎。

參考文獻：

[1]史海芳，李聰，姬永剛.序約束下單向分類方差分析模型的Bayes變量選擇[J].吉林大學學報（理學版），2021，59（05）：1093-1100.

[2]郭云東，孫有朝.基于FIS-CREAM方法的人為差錯風險評估[J].海軍航空工程學院學報，2020，35（04）：303-309.

作者簡介：顧遠陽;性別：男; 1983年 11月;上海;漢;本科;助理工程師;民航維修人為差錯評估技術探究。