基于Geogebra軟件的中職數(shù)學(xué)教學(xué)研究

吳霞　彭禮輝

摘要：中職學(xué)生學(xué)習(xí)基礎(chǔ)差，學(xué)習(xí)興趣不高，甚至有厭學(xué)情緒。為了改變沉悶的教學(xué)課堂，完善教學(xué)手段，提高教學(xué)效果，可以把信息技術(shù)與學(xué)科知識整合作為切入點。利用Geogebra軟件進行數(shù)學(xué)教學(xué)，采取數(shù)形結(jié)合和動態(tài)幾何想象手段，大大地提高了學(xué)生學(xué)習(xí)興趣，改善了教學(xué)效果。

關(guān)鍵詞：信息技術(shù)? Geogebra? 數(shù)形結(jié)合

1引言

數(shù)學(xué)課作為職業(yè)院校的一門基礎(chǔ)課，在教學(xué)過程中存在很多問題。一方面，中職學(xué)生數(shù)學(xué)基礎(chǔ)不好，學(xué)習(xí)能力差;另一方面，認知偏差嚴重，過分重視專業(yè)課，忽略文化課，尤其是數(shù)學(xué)課;最后，數(shù)學(xué)課堂上老師還是一味地采用傳統(tǒng)的教學(xué)內(nèi)容、教學(xué)方法、教學(xué)手段，使學(xué)生更加興趣低下、甚至放棄了數(shù)學(xué)的學(xué)習(xí)。對于中職生來說，對于任何專業(yè)的學(xué)生，數(shù)學(xué)是一門必要且基礎(chǔ)的學(xué)科，對學(xué)好專業(yè)課至關(guān)重要。

基于此，職業(yè)院校的數(shù)學(xué)教學(xué)必須采取信息化技術(shù)來改變教學(xué)手段。本文采用Geogebra軟件進行數(shù)學(xué)教學(xué)，不但實現(xiàn)了數(shù)形結(jié)合，而且增加了動態(tài)幾何效果，可以幫助老師完成一些即使花費大量時間和語言也無法解決的問題，從而提高學(xué)生學(xué)習(xí)興趣，改善教學(xué)質(zhì)量。

1Geogebra軟件介紹

Geogebra軟件功能強大，集幾何作圖、數(shù)據(jù)運算與處理、概率統(tǒng)計和檢測模式于一體。其包含的基本元素有直線、曲線、向量、函數(shù)等，可通過動態(tài)演示軌跡生成，展示出代數(shù)與幾何圖形的內(nèi)在關(guān)系，使得抽象的數(shù)學(xué)知識形象化。數(shù)學(xué)教學(xué)中利用GeoGebra軟件，可以給中職學(xué)生傳遞數(shù)學(xué)思想一定的視覺圖像，使數(shù)學(xué)課堂變得生動，使數(shù)學(xué)課不再抽象、無趣和復(fù)雜，而是一下子變得形象、有趣和簡單。

其特點概括如下：

⑴Geogebra軟件和學(xué)習(xí)資源均對所有人免費，方便學(xué)習(xí);

⑵Geogebra幾何屬性多樣化;

⑶從小學(xué)到大學(xué)各階段數(shù)學(xué)教學(xué)幾乎都可以采用Geogebra軟件。

動態(tài)軟件Geogebra可以節(jié)約教師備課時間，把抽象的描述進行直觀的顯示，培養(yǎng)學(xué)生主動求知的能力。

2應(yīng)用GeoGebra求解案例

2.1直線方程積件案例

采用GeoGebra制作積件，可以動態(tài)演示、真正實現(xiàn)數(shù)形結(jié)合，使學(xué)生易于理解。每個方程的積件案例有教材分析、制作積件步驟兩個方面的內(nèi)容。

已知直線L1：x+3y-2=0;直線L2：3x-2y-3=0;L3：2x+y-3=0。直線L過L1和L2的交點，并且平行于直線L3，求該直線L的方程。

⑴直線方程的教材分析

從平面解析幾何分析，某一平面上的直線就是由該平面直角坐標(biāo)系中的一個二元一次方程所表示的幾何圖形。如果要求兩條直線的交點，可以把這兩條直線的方程進行聯(lián)立求解。若聯(lián)立方程無解，則這兩條直線是平行的位置關(guān)系;若有無窮多解，則這兩條直線是重合的位置關(guān)系;若只有一個解，則這兩條直線是相交的位置關(guān)系。

⑵積件制作

①繪制直線L1。在GeoGebra操作界面輸入框中輸入“2x+3y-2=0”，點擊回車鍵繪制直線L1;

②繪制直線L2。在GeoGebra操作界面輸入框中輸入“3x-2y-3=0”，點擊回車鍵繪制直線L2;

③繪制交點A。利用GeoGebra交點工具，找到交點A點。

④繪制直線L3。在GeoGebra操作界面輸入框中輸入“2x+y-3=0”，點擊回車鍵繪制直線L2;

⑤繪制所求直線L。根據(jù)GeoGebra平行線工具，利用A點和直線L3繪制出直線L。該直線即為所求，可直接讀取直線方程：2x+y-2=0。如下圖1所示。

從以上解題過程可以看出，采用GeoGebra軟件進行求解時，不用聯(lián)立直線方程，避免了復(fù)雜的計算，對于邏輯思維較弱的學(xué)生來說，相比于傳統(tǒng)的解題方法，這種解題方式非常直觀、生動，學(xué)生更易于理解。

2.2橢圓方程積件案例

已知橢圓C：的一個焦點為（，0），離心率為。

求該橢圓C的標(biāo)準(zhǔn)方程。

⑴橢圓方程的教材分析

橢圓的標(biāo)準(zhǔn)方程共分兩種情況 （其中a^2-c^2=b^2）：

a）當(dāng)焦點在x軸時，橢圓的標(biāo)準(zhǔn)方程是：x^2/a^2+y^2/b^2=1，（a>b>0）;

b）當(dāng)焦點在y軸時，橢圓的標(biāo)準(zhǔn)方程是：y^2/a^2+x^2/b^2=1，（a>b>0）;

⑵積件制作

①創(chuàng)建滑動條。在工具欄創(chuàng)建2個滑動條a，b，類型為“數(shù)值”，區(qū)間為[1，10]，增量為1（注意a，b都不能為零）;

②繪制橢圓。在GeoGebra操作界面輸入框中輸入“”，點擊回車鍵繪制直線橢圓C;勾選“動畫”復(fù)選框，會看到大小變化的一系列橢圓。

③求焦點。去掉勾選“動畫”復(fù)選框，輸入焦點指令，求得焦點A與焦點B。

④求離心率。輸入離心率指令，求得離心率。

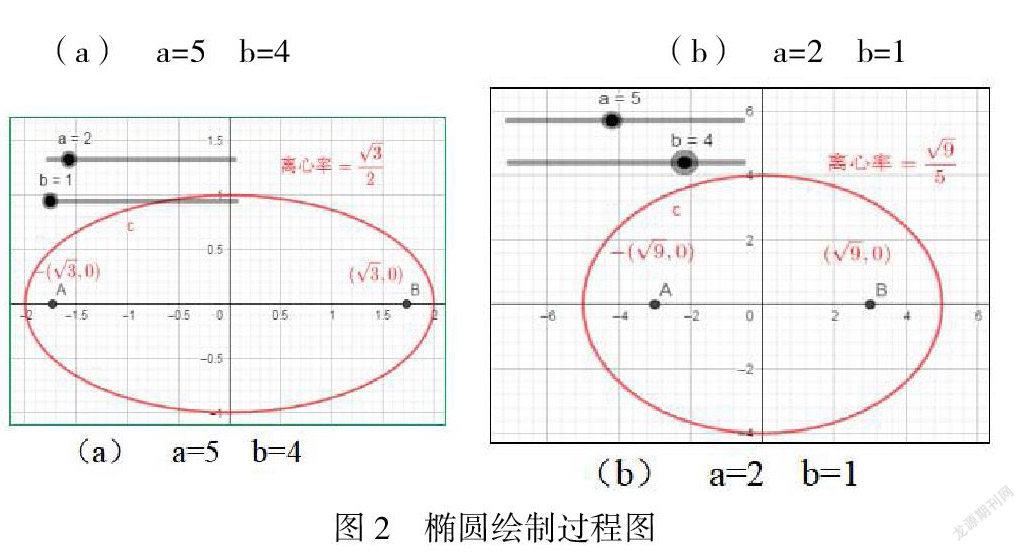
勾選“動畫”復(fù)選框，在繪圖區(qū)可以直接看到一系列變化的焦點坐標(biāo)和離心率值，當(dāng)出現(xiàn)題目中已知的焦點坐標(biāo)（，0），離心率為 時，去掉勾選“動畫”復(fù)選框，可以看到此時a=2，b=1。即橢圓標(biāo)準(zhǔn)方程為：。如下圖2所示。

（a）? a=5? b=4????????????????????? （b）? a=2? b=1

3結(jié)語

GeoGebra軟件操作簡單方便，生動直觀，可以有效減少教師課堂上展示上課內(nèi)容的負擔(dān)，提高課堂內(nèi)容展示精度，所以，與數(shù)學(xué)教學(xué)的結(jié)合將會有著巨大的發(fā)展空間。作為一名數(shù)學(xué)一線教師，將充分利用GeoGebra軟件特點，利用信息技術(shù)來提高學(xué)生學(xué)習(xí)興趣，提升課堂教學(xué)質(zhì)量。

參考文獻：

[1]江志宏. 計算機輔助中職數(shù)學(xué)空間幾何教學(xué)研究[J].教育理論研究.2016（12）：26-27.

[2]張婷.淺析大數(shù)據(jù)背景下的中職教學(xué)改革[J].黑龍江科技信息，2016（24）：75.

[3]郭衍. 動態(tài)數(shù)學(xué)軟件GeoGebra使用指南[J].中學(xué)數(shù)學(xué)教學(xué)參考.2012（1）：129-131

[4]石永福.數(shù)學(xué)的信息化教育方法探究[J].西北師范大學(xué)學(xué)報：自然科學(xué)版，2006（2）.

[5]張睿.中職數(shù)學(xué)教學(xué)與專業(yè)課融合的實踐 [J]. 科學(xué)咨詢，2019（5）.

作者簡介：吳霞，1984.11，女，湖南婁底人，碩士，講師，研究方向：數(shù)學(xué)教育。