二階非完整平面欠驅動機械系統的位置控制

黃自鑫，秦翔宇，王樂君

1. 武漢工程大學電氣信息學院，湖北 武漢430205；2. 中國地質大學（武漢）自動化學院，湖北 武漢430074

非完整系統是指一類具有非完整約束的非線性系統［1］，非完整約束可分為一階非完整系統和二階非完整系統［2］。欠驅動連桿機械系統是一類驅動關節個數少于系統自由度個數的非線性系統［3-4］，即系統的控制輸入維數少于系統位形空間的維數［5］。其中，主要研究對象為垂直欠驅動連桿系統（含重力）［6］和平面欠驅動連桿系統（不含重力）［7-8］。近年來，國內外學者針對垂直欠驅動機械系統進行了廣泛的研究。與垂直欠驅動系統相比，平面欠驅動機械系統的任意可達位置均為系統的平衡點，且該類系統的近似模型不滿足線性可控條件［9］，無法采用垂直欠驅動系統的控制方法實現其穩定控制。

其中，針對平面三連桿欠驅動機械系統，主要依據欠驅動關節的位置進行分類研究。首關節為欠驅動的平面三連桿系統是一階非完整系統，文獻［10］提出一種基于模型降階的位置控制方法，將原系統分段降階為兩個平面虛擬Acrobot 系統，并依據平面Acrobot 系統的角度約束關系進行有效控制。末關節為欠驅動的平面三連桿系統是二階非完整系統，文獻［11］將系統轉換為鏈式規范型，設計控制器進行控制。而對中間關節為欠驅動的平面三連桿系統，文獻［12］提出一種末端滑模控制的方法，當欠驅動關節的速度小于設置閾值時被鎖住，將系統控制到目標位置，該方法使被控對象不再具有欠驅動特性。基于上述分析，針對中間關節為欠驅動的平面三連桿系統的位置控制是一個開放的問題。

本文針對中間關節為欠驅動的平面三連桿系統（簡稱平面APA系統），提出一種模型降階的分段控制策略，實現系統位置控制目標。首先，控制第一連桿到達目標位置，并控制第三連桿角度和角速度為零，使系統降階為平面虛擬Pendubot。其次，基于平面Pendubot 冪零近似特性，設計一個周期性開環迭代控制器，使平面虛擬Pendubot 兩連桿的角速度為0 的同時，第一連桿回到目標位置，使原系統降階為所有連桿初始角速度為零的平面虛擬Acrobot。根據平面Acrobot 的運動狀態約束關系，以及系統末端點坐標位置和連桿之間的約束關系，利用粒子群優化算法計算第二連桿和第三連桿目標角度。最后，針對第三連桿控制目標設計控制器，實現平面虛擬Acrobot 的控制目標，從而實現平面APA系統的控制目標。

1 系統建模

平面APA系統的模型如圖1 所示。圖中，mi為第i(i= 1,2,3 )桿的質量，Li為i桿的長度，Lci為i桿的質心到前一關節的長度，Ji是i桿的轉動慣量。

根據歐拉-拉格朗日法建立系統的動力學方程為：

如圖1 所示，設欠驅動關節的位置為(XP,YP)，則欠驅動關節與系統末端點的幾何約束關系為：

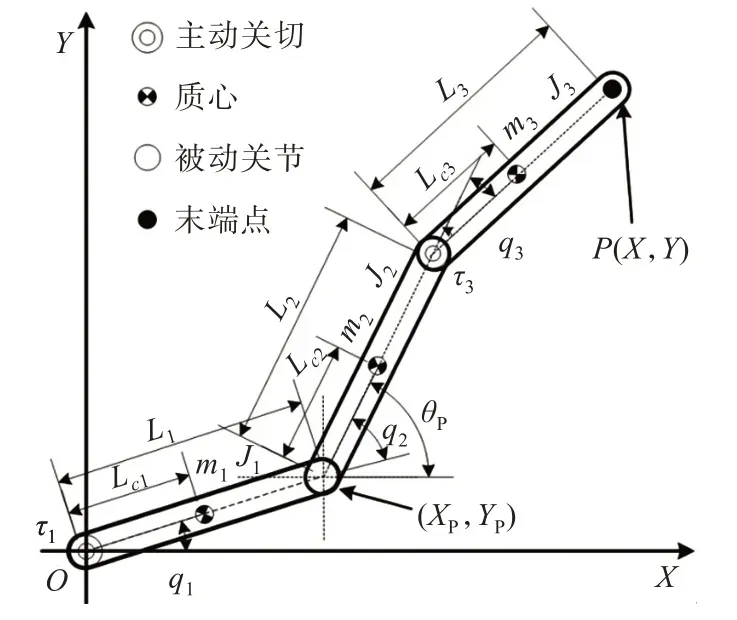
圖1 平面APA 系統Fig. 1 Planar APA system

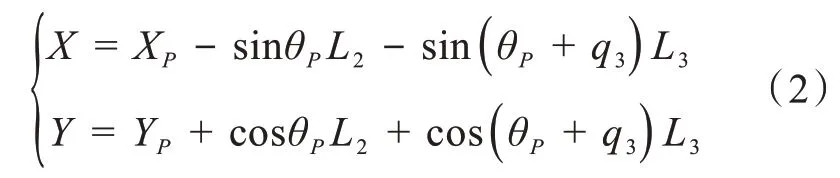
其中，XP= -sinq1L1，YP= cosq1L1，θP=q1+q2。

2 平面虛擬Pendubot控制

將平面APA系統降階為平面虛擬Pendubot，并實現欠驅動關節位置控制目標。

2.1 第一連桿目標角度求解

根據系統的目標位置來求解系統第一連桿的目標角度。 以平面APA系統目標位置為圓心(xd,yd)，平面虛擬Acrobot 兩連桿桿長之和為半徑，構建一個圓C1；以平面APA系統首關節為圓心，平面虛擬Pendubot 驅動連桿桿長為半徑，構建另一個圓C2；可得：

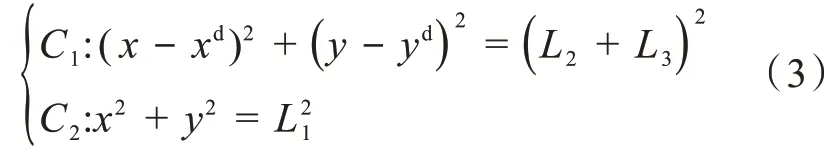
圓C1與圓C2的交點A(x1,y1)、B(x2,y2)為欠驅動關節目標范圍的極限位置。欠驅動連桿目標角度的范圍在qd1∈[ arctan (y1/x1), arctan(y2/x2)] 內就能保證平面APA系統末端點目標位置在幾何可達范圍內。

2.2 原系統降階為平面虛擬Pendubot

控制第一連桿達到目標角度，同時控制第三連桿的角度和角速度為零。

根據控制目標和平面APA系統的狀態空間方程［10］，構造Lyapunov 函數V1( )

x：

其中，e1和e2為正數。

當連桿狀態滿足條件S1時，平面APA系統被降階為一個欠驅動關節速度不為零的平面虛擬Pendubot。因此，需要對平面虛擬Penduobt進行穩定控制。

2.3 平面虛擬Pendubot穩定控制

為維持第二連桿與第三連桿為一根虛擬連桿，τ3持續保持式（10）對第三連桿持續進行控制作用。

基于以上分析，可得平面虛擬Pednubot 的部分反饋線性化形式為：

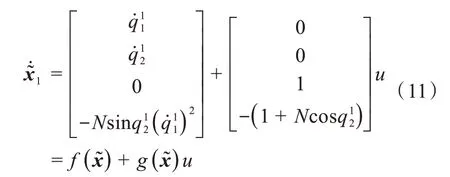
式中，N= (m2+m3)L1Lc1/(J?2+ (m2+m3)(Lc2+Lc3)2)。

模糊規則如表1 所示。

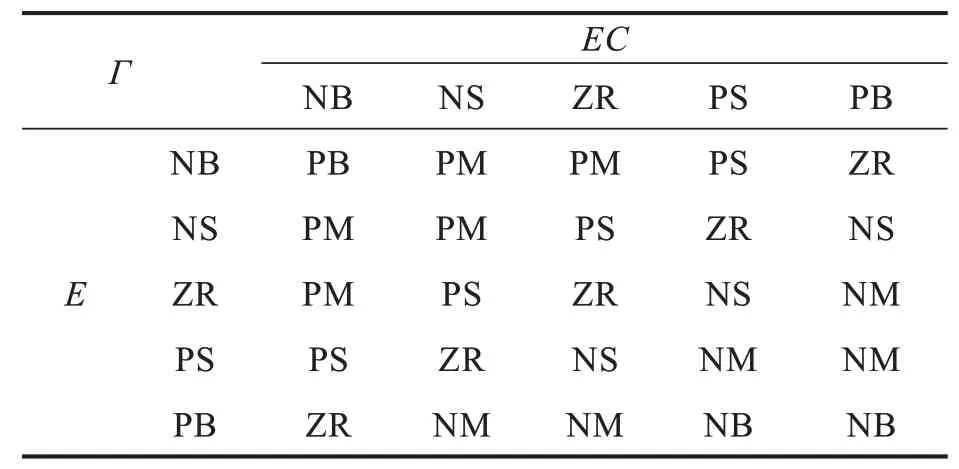
表1 模糊控制規則Tab. 1 Rules of fuzzy control

將系統總輸出乘以比例因子Γ=kout·η代入開環迭代鎮定控制器中。經過鎮定控制的平面虛擬Pendubot 達到控制目標時可以進行切換。定義切換條件S3為：

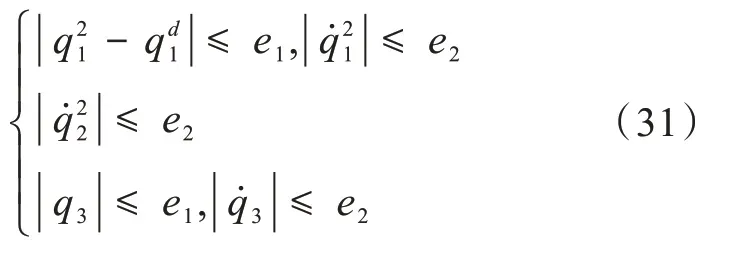
當平面APA系統連桿的狀態滿足切換條件S3時，就可以被降階為初始速度為零的平面虛擬Acrobot。

3 平面虛擬Acrobot控制

根據平面虛擬Acrobot 驅動連桿與欠驅動連桿的角度約束關系設計穩定控制器。根據平面虛擬Acrobot 的位置控制目標和幾何約束關系，利用粒子群優化算法獲得對應兩桿的目標角度。

3.1 平面虛擬Acrobot模型

3.2 基于粒子群算法的目標角度求解

根據平面虛擬Acrobot 的位置控制目標，用粒子群算法［15］進行計算其目標角度。目標函數可以定義為：

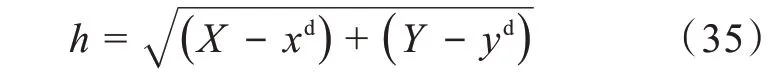
式中，(xd,yd)為平面虛擬Acrobot 的末端點目標位置，P(X,Y)為系統末端點位置，由式（2）計算可得。求解目標角度的算法步驟如下：

Step1：初始化粒子的初始位置與初始速度；

Step2：根據式（2）和式（35）計算適應度函數h；

Step3：當h( · )≤e3時，可得第三桿目標角度，否則，轉到第二步；

Step4：將第三桿目標角度代入根據角速度約束關系，求出欠驅動連桿的目標角度。

3.3 平面虛擬Acrobot系統控制器設計

根據控制目標，構造Lyapun ov 函數V2(x)：

依據LaSalle 不變原理，可得xi→qid，xi+3→0。則式（37）能實現平面虛擬Acrobot 的控制目標。

4 仿真實驗研究

利用MATLAB 數值計算工具驗證提出的控制策略的有效性，平面APA系統的模型參數如表2所示。

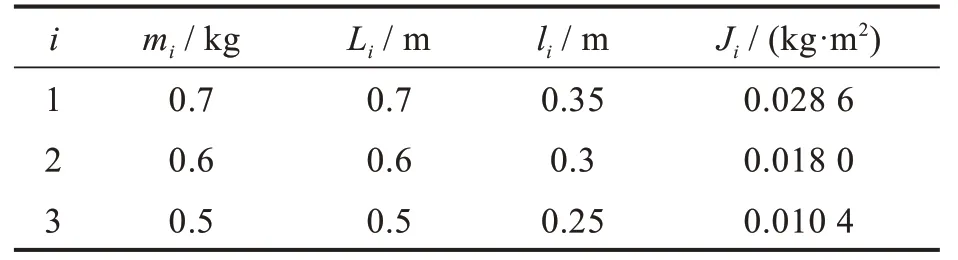
表2 平面APA 系統模型參數Tab. 2 Model parameters of planar APA system

系統的初始狀態為：

如圖2 所示，角度、角速度都收斂到目標狀態，末端點也穩定到目標位置。系統驅動桿的驅動力矩始終保持在20 N·m 以內，力矩較小。在13.17 s時，系統從第一階段切換到第二階段；在23.67 s時，系統從第二階段切換到第三階段；在33.79 s時，系統各連桿均到達目標角度，從而平面APA系統末端點也到達目標位置。

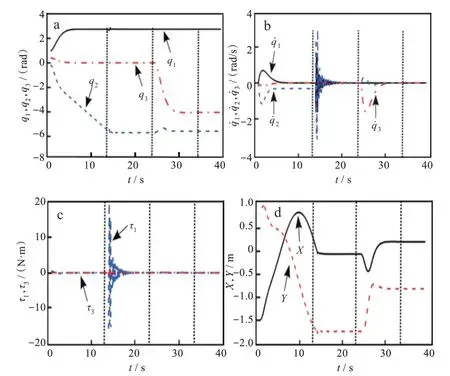
圖2 仿真結果：（a）角度，（b）角速度，（c）控制力矩，（d）位置Fig. 2 Simulation results：（a）angle，（b）angular velocity，（c）control torque，（d）position

5 結 論

針對平面APA系統末端點位置控制問題，本文提出了一種基于模型降階的控制策略。將平面APA系統末端點位置控制問題轉化為平面虛擬Pendubot 的穩定控制問題和平面虛擬Acrobot 的位置控制問題。首先，基于開環迭代控制實現平面虛擬Pendubot 的穩定控制。其次，針對平面虛擬Acrobot，借助角度約束關系，采用粒子群算法計算各連桿角度，直接控制驅動連桿到達目標角度，并間接實現欠驅動連桿的控制角度目標，并最終實現平面APA系統末端點位置控制。