一種改進型關聯規則算法設計與研究

鄧 毅，鄧曉慧

（1.重慶科創職業學院 人工智能學院，重慶 永川 402160 2.重慶城市職業學院 商學院，重慶 永川 402160）

1 Apriori算法概述

AIS算法是較早被用來解決關聯規則問題的算法，但此算法在使用的過程中性能較低，于是Agrawal等人在此前的應用基礎上，對AIS算法進行了相關的改造，Apriori算法此時便被提出來了，且成為利用關聯規則進行數據挖掘較好算法之一[1]。依據Apriori算法，延伸出了類似Apriori-Hybrid、DIC、AprioriTid、DHP等算法。

1.1 Apriori算法過程

在Apriori算法運行之前，用戶需要首先設定好最小支持度，一旦開始掃描事務數據庫時，就僅計算每一個項目的具體值的數量，來確定大型1--項集，后面的n次遍歷，都將重復連接與剪枝的操作，直到產生的項為空，停止算法。該算法的流程圖如圖1所示[2]。

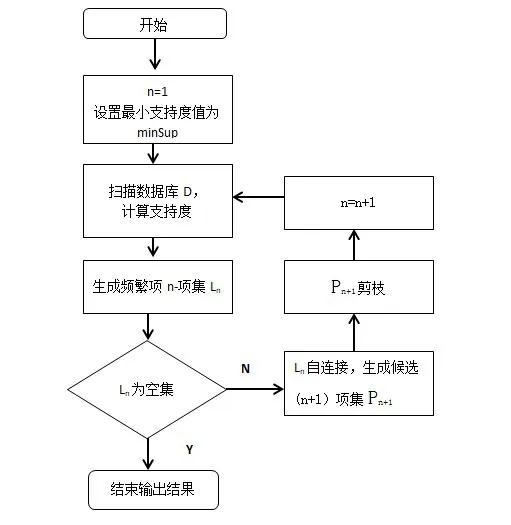
圖1 算法執行過程

該算法通過逐層的迭代來得到需要的頻繁項集，獲取頻繁項集的算法偽代碼如下所示：

算法：Apriori算法生成頻繁項集

輸入：事務庫D；最小支持度閥值minSup

輸出：D中的頻繁項集L

方法：

L1={發現頻繁1-項集}；

For(n=2;Ln-1≠φ;n++)

{

Cn=apriori_produce(Ln-1,minSup);

for each transactionT∈D{

CT=sub set(Cn,T);

for all candidate c∈CT

C.count++;

}

Ln={c∈Cn|c.count≥min Sup}

}

Return L={UnLn}

在該算法的偽代碼方法中，Ln-1和min S up這兩個值作為函數apriori_produce的參數值被代入，獲取了候選n-項集Cn,這個函數進行了兩個操作：連接操作、剪枝操作，如下所示的實現步驟[3]：

Function apriori_gen(Ln-1,minsup)

For each itemset S1∈Ln-1

For each itemset S2∈Ln-1

c=s1?s2;

If exist_infrenquent_subset(c,Ln-1)

{

Delete c;

}

Else fill cnwith c;

}

Return cn

在完成了上述的n--項集后，使用Apriori的性質，需要對Cn進行剪枝的操作，刪除掉擁有非頻繁子集的候選。用于對非頻繁子集測試的函數實現如下：

Function exist_infrenquent_subset(c,Ln-1)

for each(n-1)-subset p of c

If p?Ln-1

Return true;

Return false;

1.2 Apriori算法實例解析

由于偽代碼語言并不能夠清晰的說明Apriori算法的執行過程，接下來將通過一個使用該算法產生關聯規則的例子來說明。如表1所示的交易數據庫Q。

表1 交易數據庫Q

在算法實施的過程中，支持度用項集出現的次數來表示，設定挖掘的過程中，最小支持度的閥值為2，該算法的執行步驟如下：

首先，生產頻繁項集。當對交易數據庫Q完成掃描后，會得到候選1-項集C1：{M1}、{M2}、{M3}、{M4}、{M5}。因為生成的每個項集的支持度的值都大于或者等于設定的2，所以C1中的所有的項集都被包含在1-項集L1中。

對第一環節中的1-項集L1進行自連接，得到候選2-項集C2：{M1,M2}、{M1,M3}、{M1,M4}、{M1,M5}、{M2,M3}、{M2,M4}、{M2,M5}、{M3,M4}、{M3,M5}、{M4,M5}，在L1中包含了他們所有的子集，不需要剪枝操作[4]。接著完成這些候選項集的支持度計算，結果如下：{M1,M4}、{M3,M4}、{M3,M5}、{M4,M5}支持度的值小于設定的閥值2。說明這些不是頻繁2-項集的內容，其余都是。

2-項集C2進行自連接操作產生3-項集C3：{M1,M2,M3}、{M1,M2,M5}、{M1,M3,M5}、{M1,M3,M4}、{M2,M3,M5}、{M2,M4,M5}。因為{M3,M5}、{M3,M4}、{M4,M5}都不在L2里面，所以可根據Apriori的性質得出后面四個選項是可以被剪枝的。只需要對候選項集{M1,M2,M3}、{M1,M2,M5}進行計數，就可以獲得3-項集C3。

3-項集L3進行自連接就可以獲取到4-項集C4：{M1,M2,M3,M5}，由于{M1,M3,M5}不在L3里面，所以要進行剪枝，最后得到L4為空集，到此為止，算法計算完成。

最后經過Apriori算法得到的頻繁項集為：{M1}、{M2}、{M3}、{M4}、{M5}、{M1,M2}、{M1,M3}、{M1,M5}、{M2,M3}、{M2,M4}、{M2,M5}、{M1,M2,M3}、{M1,M2,M5}。

然后，將以上得到的所有的頻繁項集繼續處理，得到需要的強關聯規則。拿{M1.M2,M3}為例進行說明，{M1,M2,M3}的全部非空子集為：{M1}、{M2}、{M3}、{M1,M2}、{M1,M3}、{M2,M3}，那么可能的關聯規則計算如下：

如果將最小置信度的閥值設定為40%，那么就可以將上述計算得到的Confidence的值與設定的40%進行比較，選取其中大于該值的規則。從上面的計算結果來看，第4、5、6條規則滿足條件，即得到這幾條是強關聯規則。

按照以上的方法對其他的頻繁項項進行類似的操作，就可以得到全部的規則。

2 Apriori算法的性能分析

Apriori算法的核心思想為：候選產生-檢查。這種方法的優點為：對候選K-項集采取了有效的裁剪，可以大大的降低了候選集的大小，從而減少了計算量。缺點為：當設定的最小支持度的閥值比較小，相反事務集量較大，就會表現出性能上的不足，主要體現在以下幾個方面[5]。

第一掃描事務數據庫次數較多；

第二可能會生成較大的候選集；

第三產生過多的無用的規則。

2.1 Apriori算法的優化

通過上文對Apriori算法的介紹和分析，該算法容易被人理解和接受，但是其也存在需要解決的問題，需要對該算法進行部分的優化。通過查閱相關的文獻資料，專家及學者對該算法的優化思想，主要有以下幾個方面。

2.1.1 基于哈希的方法

該方法的主要思想為：將哈希技術運用到頻繁2-項集的獲取上面。如果最小支持度的閥值大于某一個K-項集在哈希樹路徑上的計數值，那么該項不會是頻繁的。

2.1.2 降低交易個數的方法

該方法的原理為：不包括任何K-項集的事務一定不包括（K+1）項集。通過使用該方法減少未來需要掃描的事務記錄，從而提高算法的效率[6]。

2.1.3 基于采樣的方法

該方法通過抽取數據集中的部分數據作為樣本，得到可能在整個數據集中成立的規則，然后利用未作為樣本的數據進行規則的驗證。此種方法減少了I/O的操作，但是降低了數據的精度，可能會導致數據扭曲，針對此種現象，很多學者也討論了反扭曲的相關算法[7]。

2.1.4 間隔計算的方法

該方法的過程為：首先由CK直接生成CK+1，得到CK+1的支持度進而獲取LK+1，從而不需要計算的CK支持度來獲LK，減少了數據庫的一次掃描。使用該方法的前提條件是生成的候選項目集CK+1要能夠被放進內存。

3 Apriori算法改進

3.1 Apriori算法改進思想

通過對Apriori算法性能及算法思想的分析，該算法還是存在一定的缺陷[8]。盡管很多的專家學者針對某些缺陷，提出了一些解決方法，但仍然有掃描事務數據庫次數較多，準確度不精準的問題，主要體現在以下兩個方面：

第一為了獲取候選頻繁集的支持度，需要多次掃描事務庫，I/O的開銷很大，當數據的量較大時，算法的執行效率低下，花費的時間較長[9]。

第二在頻繁集連接時，沒有考慮到現實的意義，讓很多無關項集參與到了連接，導致了大量的候選項集產生，最后也導致了自連接和后剪枝的量的增加。

在本次的研究中，針對第2個問題進行改進，主要在原Apriori算法基礎上引入事先剪枝的方法，來降低候選集的數目，從而提高數據挖掘的效率。

3.2 事先剪枝策略

Apriori原算法是LK-1在進行自連接后，可以得到候選集CK，利用算法的性質對CK進行剪枝操作。改進之后的思想為：如果在CK被生成之前就能夠判斷出那些非頻繁，那么就可以提前剪掉這些項集。優點為：避免了為產生這些項集的連接操作，同時也省去了在掃描事務庫時的支持度頻度需要計算的問題，進而減少了算法計算的時間，下面結合頻繁項集的幾個性質來進行算法改進的說明。

第一如果K-項集X是頻繁項集，那么X下的全部（K-1）項子集都是頻繁項集；

第二如果K-項集X里面（K-1）項子集不是頻繁項集，那么X就不會是頻繁項目集；

第三如果K-項集X={i1,i2,...,ik}中，滿足S∈X，且LK-1(S)

對第3條性質進行證明：若X是頻繁K-項集，則LK-1包含K個K-1項子集。在這些子集中，單個項目S(S∈X)總計出現了k-1次，因此對?S∈X，都滿足|LK-1(S)|≥K-1，和條件矛盾，所以X不是頻繁項目集。

由第三條性質可以得到，如果LK-1里面有元素L包含了s,滿足|LK-1(S)|≥K-1，那么LK-1中除去之外的L全部元素與L連接，得到的K-項集全部不是頻繁項目集。由L進行連接得到的候選K-項集是非頻繁的，就不需要讓L加入連接。

結合上述的相關性質，具體的事先剪枝實施步 驟 如 下 ：第 一 算 出 |LK-1(S)|，其 中S∈{?A|A∈LK-1}，則算出LK-1中單個項目出現的次數；第二記錄頻度低于K-1的項目，標記為U={S||LK-1(S)

在完成第4步的L'K-1的自連接之后，使用原Apriori中的后剪枝可以進一步的減少候選集的規模。使用改進的事先剪枝策略可以實現降低頻繁項集連接操作的時間花銷，也實現了降低后剪枝操作時的工作量。使用該策略減少了候選項集的數量，同時變相的也減少了掃描數據庫的I/O開銷，降低了算法的運行的時間復雜度[10]。

4 算法改進性能評價

為了能夠獲取改進后算法的性能，本小結將改進前后的算法進行比較分析。實驗比較的數據分為兩個方面：在不同的最小支持度閥值下，產生的候選集數量和運行的時間。

實驗環境：

操作系統：windows 7 Professional。

仿真環境：Matlab R2012a。

測試使用數據：選取UCI標準測試數據集Mushroom,此種數據的特征就是頻繁項目集密集分布。

實驗步驟：

第一使用相同的數據集，設置不同的最小支持度閥值，比較改進前后的不同支持度下的候選集數量，如圖2所示。隨著最小支持度的閥值的增加，候選集的數目都在減少，但是在相同的支持度下，改進后的算法生成的候選集數目要少于改進前。

圖2 不同支持度下的候選項集

第二使用相同的數據集，設置不同的最小支持度閥值，比較改進前后的運行時間，如圖3所示。通過實驗結果表明：改進過后的算法在不同的支持度下的運行時間都要小于改進之前的運行時間。

圖3 不同支持度下的運行時間

5 基于U檢驗思想置信度評價

在實際的關聯規則挖掘中，基于傳統的支持度-置信度的Apriori算法存在著一些問題。例如：不能夠得到更加有效的關聯規則。針對此問題，本論文在研究時，在Apriori算法基礎上，采用了基于U檢驗思想衡量標準，即：通過限制、約束關聯規則的產生方式，得到需要的強關聯規則。

U檢驗數學算法思想：設一個擁有K屬性的總體樣本為S，對象的總個數為計為n,擁有K屬性的對象個數為m,那么具備該條件的對象在S中的比率為：P=m/n。使用U檢驗，可以比較總體百分數P0與樣本百分數P之間的差異。該差異值用標準差SP，計算公式如下所示。

利用以上的兩個公式，可以得到如下的差異關系：

(1)|u|

(2)u0.05≤|u|

(3)|u|≥u0.01，p與p0顯著性差異很大。

在事務集L中，一個X項對另外一個Y項的影響度的大小，可以利用期望置信度及置信度之間的差異來表現。結合上述的公式，得到關聯規則的影響度定義公式如下：

若P(Y)=1且P(X)<1,規則的影響度值為0;

當滿足最小支持度和最小置信度時，依據影響度，可以將支持度-置信度生成的規則分為三類，如表2所示。

表2 關聯規則分類a

在T分布下，一個樣本容量為n,ua表示為顯著水平為a下的臨界值u的最小影響度。如果n的值比較的大，可以得到ta(n)≈ua，ua為臨界u值。如果e ffect(x?y)>ua，那么此時得到的關聯規則為正關聯規則，是值得研究的規則。一般取a=0.05作為顯著性校驗水準，此時得到u0.05=1.96。依據臨界值的大小和影響度的大小，在本次的研究中，表明可以得到置信度較高的規則。

6 結語

本文在針對關聯規則算法Apriori算法掃描次數過多、產生過多無關規則及算法效率不高的問題，采用了事先剪枝的方法進行改進，通過使用Matlab對改進的算法進行了評測，同時使用了U檢驗思想衡量標準的算法對評測的結果進行信度測算，實驗結果表明，改進后的算法較好的解決了以上的問題，在后續的研究中，可以進一步的優化算法產生更強的關聯性規則。