考慮外界影響的元動作單元故障概率模型

鞠萍華，谷豪東，許文林，黃廣全

（重慶大學 機械工程學院，重慶 400044）

對于數控機床而言，其功能是通過各個部件運動來實現的，而部件的運動則是由一個個基本動作完成的.元動作單元結構化分解就是根據這一特點，將產品按照“功能（function）－運動（motion）－動作（action），FMA”進行分解，其中心思想就是將實現產品功能的復雜的綜合運動拆分為一系列基本的動作.將分解得到的最基本的動作稱為元動作，將實現元動作的單元稱為元動作單元（Meta-action unit，MAU）.一直以來，關于數控機床可靠性的研究比較多，但元動作單元可靠性的研究則比較缺失.元動作單元作為組成數控機床的基本構件，研究其故障概率模型將對數控機床組成構件的可靠性研究有著重要作用.

為得到元動作單元故障概率模型，首先需要對元動作單元產生的故障進行分類.在本文研究之前，對元動作單元故障進行分類的方法有很多，這些方法分別根據不同的標準進行分類.有根據元動作單元故障發生的位置，將元動作單元的故障分為內部故障、連接型故障和控制系統故障[1]；還有按照故障發生和發展的進程將故障分為突發性故障和漸發性故障；除此之外，還有根據觀察到的故障現象將故障分為動態異常和靜態異常兩種類型[2].這些分類方式可以由故障結果直接進行判定，分類比較方便，但不利于得到元動作單元的故障概率模型.

除此之外，對各種機電設備進行分類并得到故障概率模型的研究也有很多，這些概率模型分別使用了不同的分布.其中最簡單和常用的是選用泊松分布對故障數據進行描述[3-4]，使用泊松分布描述設備故障是最簡單直接的.但泊松分布展現的故障率是恒定的，而機電設備則會由于老化導致故障率不斷增加，因此單純使用泊松分布不能對故障數據進行描述.Xie 等[5]提出用指數分布函數對故障率進行描述.然而，這種方法卻將老化故障當作隨機故障，無法解釋老化故障的故障率隨時間增加的趨勢.Li[6]提出了使用正態分布和威布爾分布.這種方法可以得到故障率分布，但是這種方法卻有一個缺點，其認為隨機故障的故障率隨時間改變.

上述故障概率模型在描述元動作單元故障數據時存在各種各樣的缺陷，本文針對元動作單元的特點，建立元動作單元的故障概率模型.

1 元動作單元

元動作是數控機床進行FMA 結構化分解中得到的最基本的動作，其具體的分解步驟如圖1 所示.根據元動作的特點，在此將元動作的概念定義為：元動作為機電產品中傳遞運動和動力的最基本形式，它是機械產品中最小的運動[7].

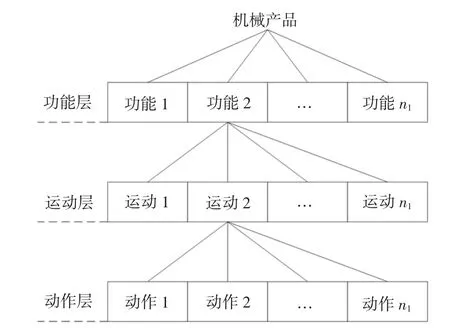
圖1 FMA 結構化分解示意圖Fig.1 FMA structured decomposition diagram

單個零件是無法完成一個規定的元動作，需要一個完整的單元才能實現.元動作單元為能夠保證機械產品的元動作得以正常運行的所有零件按照裝配關系組成的統一整體，且元動作單元在結構上不可再分也無需再分[7].

復雜的機電產品的功能是由部件的運動來實現，部件的運動是由一系列元動作來實現，而完成一個元動作則需要一個元動作單元.因此當產品發生故障時，最終體現在元動作單元上.而元動作單元的故障是指部分動作單元功能失效，造成不能順利完成規定動作要求的狀態[1].當元動作單元出現故障時，會導致部件的運動出現障礙，最終體現在機電產品出現故障.以數控機床為例，數控機床的運動由機床的進給、工作臺的回轉、刀架的回轉、從刀庫抓取刀具、主軸的回轉等功能實現.而刀架的回轉分為刀架的移動和轉動，而對于這兩個運動來說，需要兩個元動作單元來分別實現.當其中一個元動作單元發生故障時，刀具回轉將無法實現，進而數控機床無法工作[8].因此研究單個元動作單元的故障概率模型對于研究數控機床的可靠性來說，十分重要.其故障概率模型的建立過程如圖2 所示.

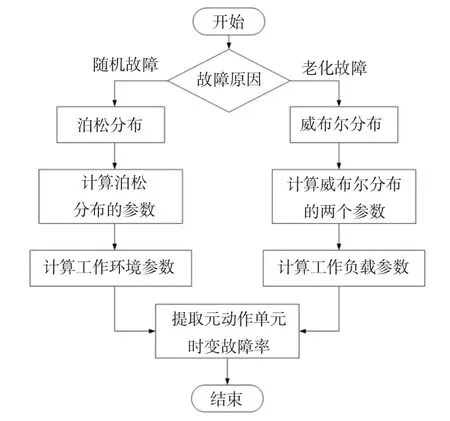
圖2 元動作單元故障概率模型流程圖Fig.2 Flow chart of failure probability model of meta-action unit

2 元動作單元的故障

對于數控機床而言，從安裝完成、投入運營到報廢的整個過程的故障率曲線應該如圖3 所示，呈現出浴盆曲線的形狀[9].早期故障的發生原因在于設計和制造階段的缺陷，并且故障率隨著時間慢慢下降；一段時間后，進入偶然故障期，數控機床工作的大部分時間處于偶然故障期，故障率逐漸穩定，在此期間，由于疲勞和磨損的原因，故障率隨時間略微增加，并不為常數；隨著時間的增加，由于老化等原因，故障率不斷增加，數控機床進入耗損故障期[10].數控機床在交付時會經歷充分的試驗安裝，早期故障期較短，其故障率主要集中在浴盆曲線的偶然故障期和耗損故障期.元動作單元是組成數控機床的最基本單元，其故障率曲線也應該集中在偶然故障期和耗損故障期.

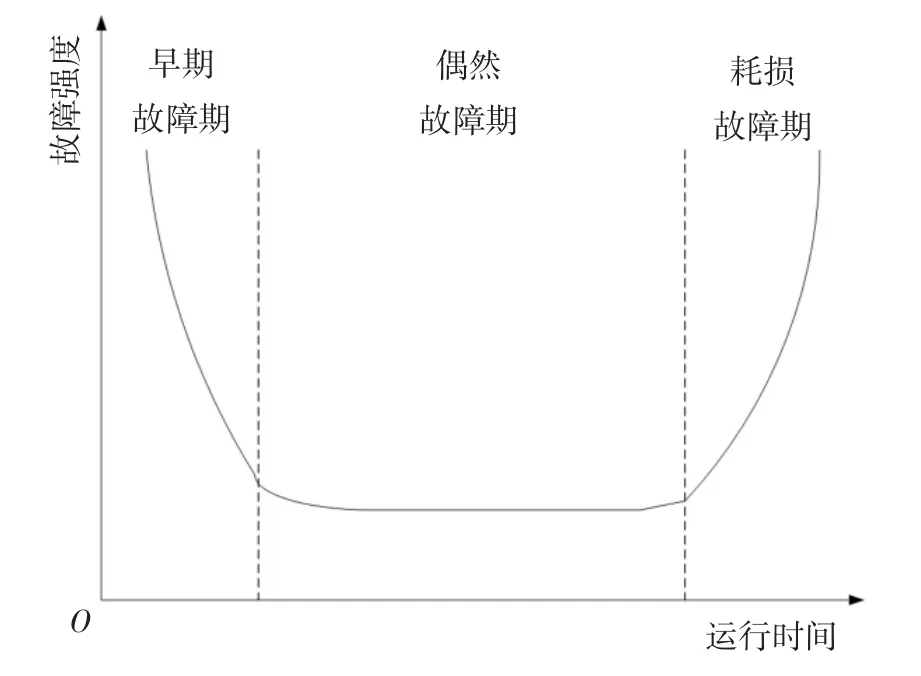
圖3 浴盆曲線示意圖Fig.3 Schematic diagram of bathtub curve

為了確定元動作單元的故障概率模型，需要對其發生的故障進行分類.本文根據元動作單元故障發生的原因將故障分為老化故障和隨機故障.元動作單元在運行過程中由于老化失效而造成的故障稱為老化故障；由于一些偶然因素而造成的故障則稱為隨機故障.

元動作單元是一個關于結構的概念，包含的結構種類非常多，發生的不同類型故障也很多，除此之外，引發同一種故障背后的原因也可能有多種，因此根據故障發生的原因將故障進行分類在操作上會有一些復雜.例如，田致富在論文中對刀架轉動異響故障樹分析，其結構如圖4 所示，引起異響的原因有緊固件松動、嚙合區有異物和潤滑不充分[11].其中嚙合區有異物和潤滑不充分為偶然因素造成的故障，緊固件松動有可能是因為老化因素造成的故障，也有可能由于操作過程中偶然因素造成的故障.

圖4 刀架轉動異響故障樹Fig.4 Fault tree for abnormal noise of machine tool holder rotation

在對元動作單元故障實際進行分類中，可參考以下方法，老化故障是元動作單元在工作過程中組成零件的技術指標逐漸下降，最終超出允許的范圍而發生故障，可以在事先發現征兆，具有可預測性；隨機故障是元動作單元由于偶然因素突發的故障，一般沒有任何征兆，具有不可預測性.

為對元動作單元發生的故障進行準確分類，從而確定元動作單元故障概率模型，故障數據的收集不僅要記錄故障發生的時間，還要記錄發生的部位和發生的具體情形，以便于確定引起故障原因，從而對元動作單元發生的故障進行分類.

3 建立元動作單元的故障概率模型

由于兩種故障不同的數據分布特點，所以應選擇兩個不同的概率分布函數來分別對其進行描述.除此之外，兩種故障類型分屬于兩個獨立的部分，所以最后得到的用來擬合元動作單元故障概率模型應為兩個不同故障概率分布直接相加.

當故障數據具有三個特點時，可以選用泊松分布來進行描述[12]：

①物體在某段時間內發生n 次故障的概率與時間起點無關，僅與該段時間的長短有關.

②在兩段相互不重疊的時間內，物體發生故障的次數n1和n2是相互獨立的.

③在較短的時間內，物體發生兩次或更多故障的概率很小.

元動作單元的隨機故障是由元動作單元內外的偶然因素導致的，例如，帶傳動的帶突然斷裂，異物進入元動作單元內等.這些因素隨機發生，導致元動作單元發生故障，相互之間沒有關聯.因此發生n 次故障的概率與時間起點無關，僅與時間長度有關；且互不重疊的時間內，發生故障的次數相互獨立；另外，元動作單元是針對機械產品的概念，除特殊情況外，機械產品的壽命較長，可靠性也較高，發生故障的概率較低.綜上所述，元動作單元隨機故障數據的特點符合泊松分布的要求，故隨機故障選用泊松分布進行描述.泊松分布的故障率的計算如式（1）所示：

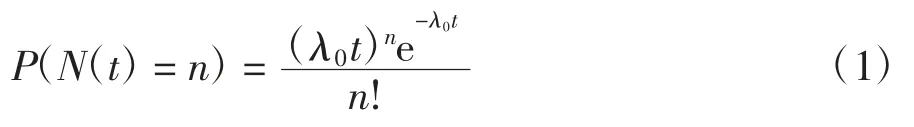
式中：n 為故障發生的次數，λ0表示故障率，t 為時間.

老化故障是由于元動作單元運行過程中老化失效而發生的故障，例如：齒輪磨損，緊固件老化松動等.老化故障的故障率隨時間的增長而逐漸增加，因此應采用當參數變化時，概率分布函數形狀隨之改變的威布爾分布函數.

威布爾分布的分布函數和故障率分別如式（2）和（3）所示：

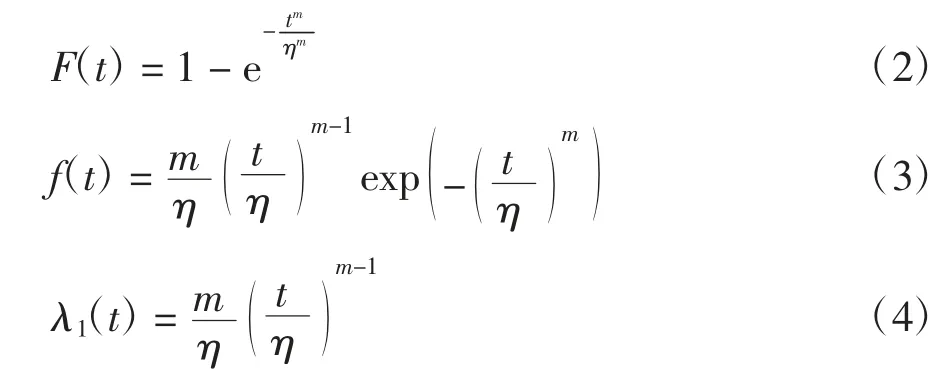
其中：η 是比例參數，m 是形狀參數，t 為時間

當威布爾分布形狀參數改變時故障率隨時間變化的情況如圖5 所示.當m=1，則威布爾分布為指數分布，故障率為常數；當m<1，則故障概率隨時間減小；當m>1，則故障率隨時間增加[13].故當m>1時，威布爾分布適合描述老化過程.

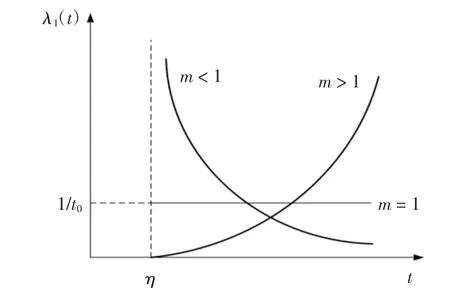
圖5 形狀參數不同時威布爾分布故障概率圖Fig.5 Failure probability diagram of Weibull distribution with different shape parameters

由于兩種類型的故障相互獨立，所以元動作單元故障率λ（t）應為兩個不同分布的故障率之和，如式（5）所示：

當t=0 時，元動作單元故障率為λ0；當選擇m>1 時，隨著時間t 逐漸增加，元動作單元故障率隨著時間慢慢增加，符合實際情況.

4 元動作單元故障模型參數估計

元動作單元故障概率模型由獨立的兩個分布組成，泊松分布和威布爾分布，兩種分布屬于不同的類型，進行參數估計時應將兩個分布分別進行估計.由泊松分布的性質可知，其故障率可以由式（6）計算：

式中：n 為元動作單元發生隨機故障的次數，ti為發生隨機故障的元動作單元的運行時間，tj為未發生隨機故障的元動作單元的運行時間，Z1、Z2分別代表兩種類型的元動作單元.

常用的威布爾分布參數估計方法有三種，極大似然估計、最小二乘法、矩估計法[14].三種參數估計方法中，矩估計法和極大似然估計法精度高于最小二乘法[15]，本文選用矩估計法進行參數估計.

由威布爾分布的性質可知，其均值M 和方差S2分別由比例參數m 和形狀參數η 來決定：

比例參數m 通過式（7）和式（8）消除后得到只含有形狀參數η 的方程（9）.

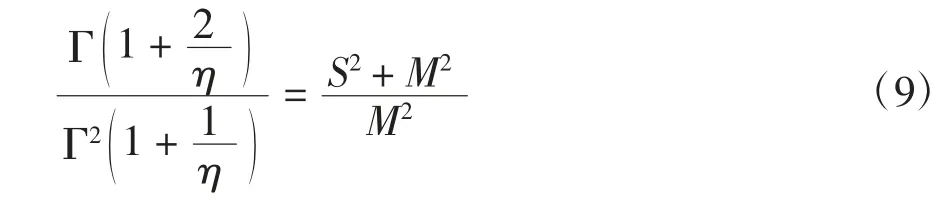
由統計得到的故障數據分別計算一階樣本矩M和二階樣本矩S2得：

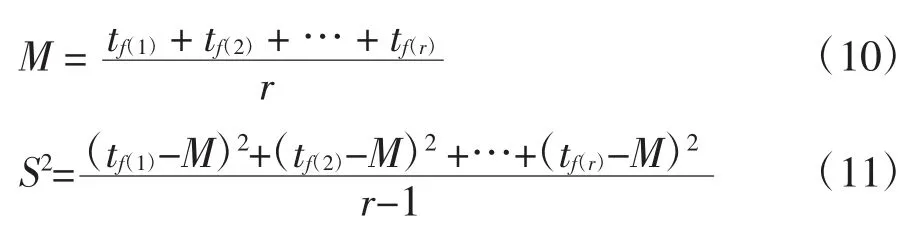
對于Γ 函數而言，存在以下性質：

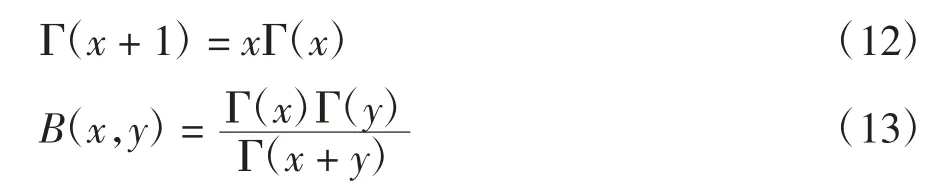
式中：B 函數為Beta 函數.

因此，對式（9）中包含的Γ 函數進行轉化可以得到：

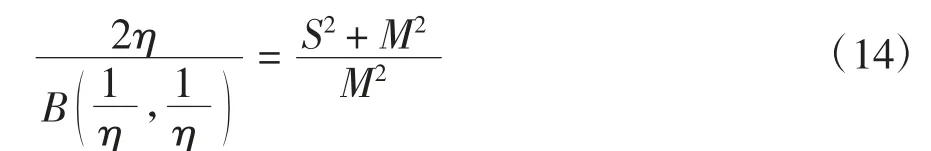
對于一組統計得到的故障數據來說，S2和M 確定，方程（9）的右邊相當于常數.方程（10）為關于η的一元方程，方程左邊為關于η 的函數，則方程的解應為函數f（η）與常數交點的橫坐標.由B 函數的性質可知，函數f（η）在（0，+∞）內單調遞減，隨著η 增加，函數無限接近于0，因此方程（9）有且只有一個解[16].方程可以通過二分法進行數值計算得到唯一確定的形狀參數η，求得η 后，根據式（7）則可以求得比例參數m.

5 元動作單元工作負載參數和工作環境參數的估計

元動作單元在工作過程中，其故障率勢必會受到外界因素的影響.本文中，故障類型被分為兩類，老化故障和隨機故障.在外界影響因素中，工作負載和工作環境會對兩種故障類型的故障率分別造成影響.為比較各個工作地區的工作負載和工作環境對元動作單元故障率的影響，本文分別采用工作負載參數和工作環境參數.

元動作單元工作過程中，工作負載越大，則老化速度就越快，所以應在威布爾分布中添加工作負載參數.而工作環境會對隨機故障的故障率造成影響，應對泊松分布添加工作環境參數[17].

當平均負載不斷增大時，設備老化的速度不斷加快，比例參數η 往往與工作負載的大小有關，負載越大，比例參數越小[12]，因此工作負載參數Rl應表現在威布爾分布的比例參數上；由于工作環境會直接影響隨機故障的故障率，且泊松分布只有故障率λ一個參數，所以工作環境參數Re應直接表現在泊松分布的故障率上.

工作負載參數Rl和工作環境參數Re的估計方法和步驟如圖6 所示.當工作負載參數Rl大于1，則說明對該元動作單元來說工作負載小于平均水平，如果小于1 則說明工作負載大于平均水平；且工作負載參數越大，則說明工作負載越小；反之，參數越小，則說明工作負載越大.

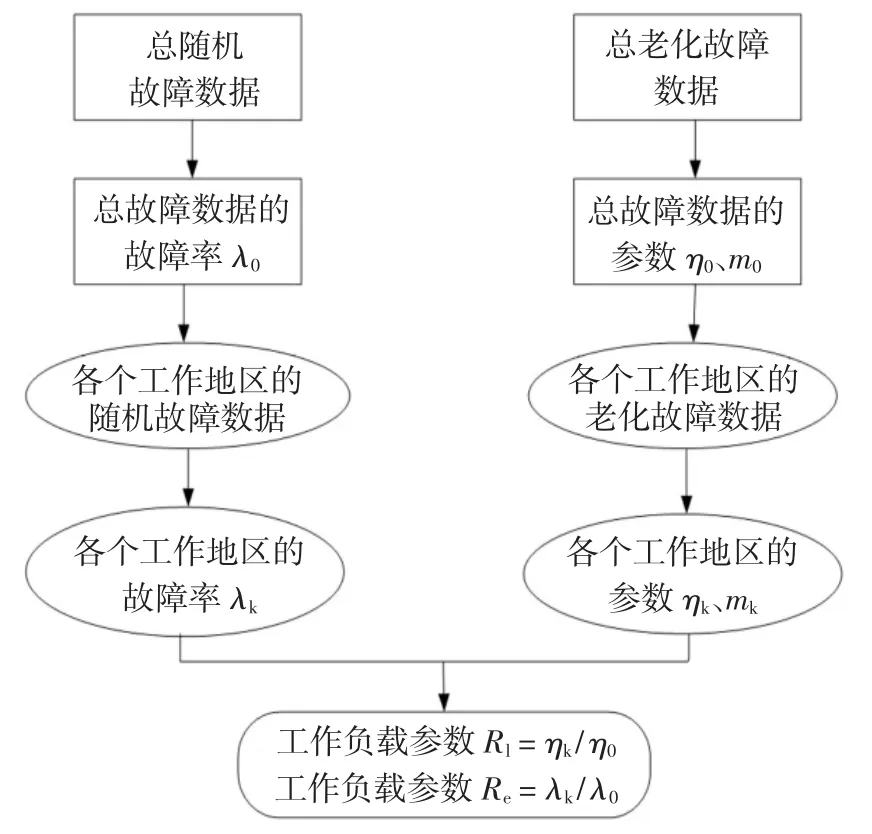
圖6 確定工作負載參數和工作環境參數流程圖Fig.6 Flow chart for determining working load parameters and working environment parameter

工作環境參數Re則相反，如果大于1，則說明工作環境比平均水平更惡劣，如果小于1，則說明工作環境比平均水平更優；除此之外，工作環境參數越大，則說明工作環境更差，反之，則說明工作環境更好.

6 算例分析

某批次數控機床CJK1630 共計116 臺平均分成四組，交付用戶使用便開始進行現場試驗，選取其中重要的轉動元動作單元（主軸軸系結構），待所有機床的該元動作單元都出現故障，則數據收集結束，主軸的故障類型如圖7 所示.

圖7 主軸故障圖Fig.7 Spindle failure diagram

將統計得到的故障數據按照故障發生的原因進行分類后，得到的隨機故障數據和老化故障數據分別如表1、表2 所示.

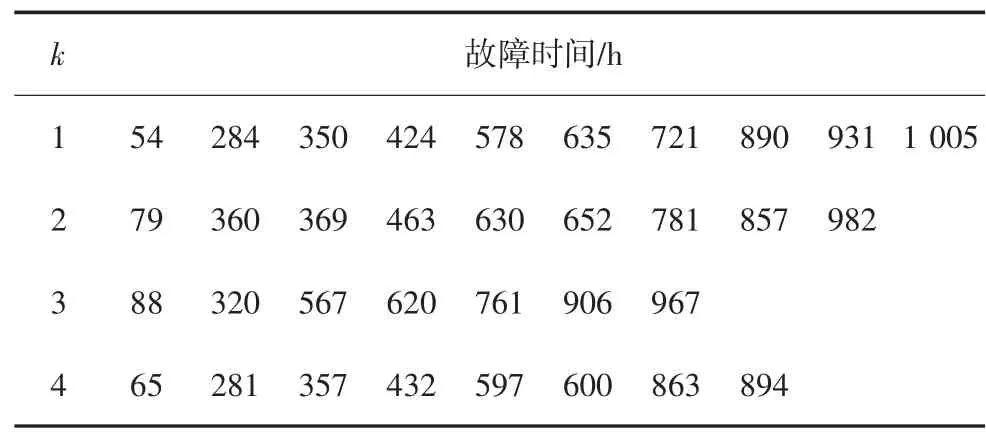
表1 元動作單元隨機故障數據Tab.1 Failure data for random failures of meta-action units

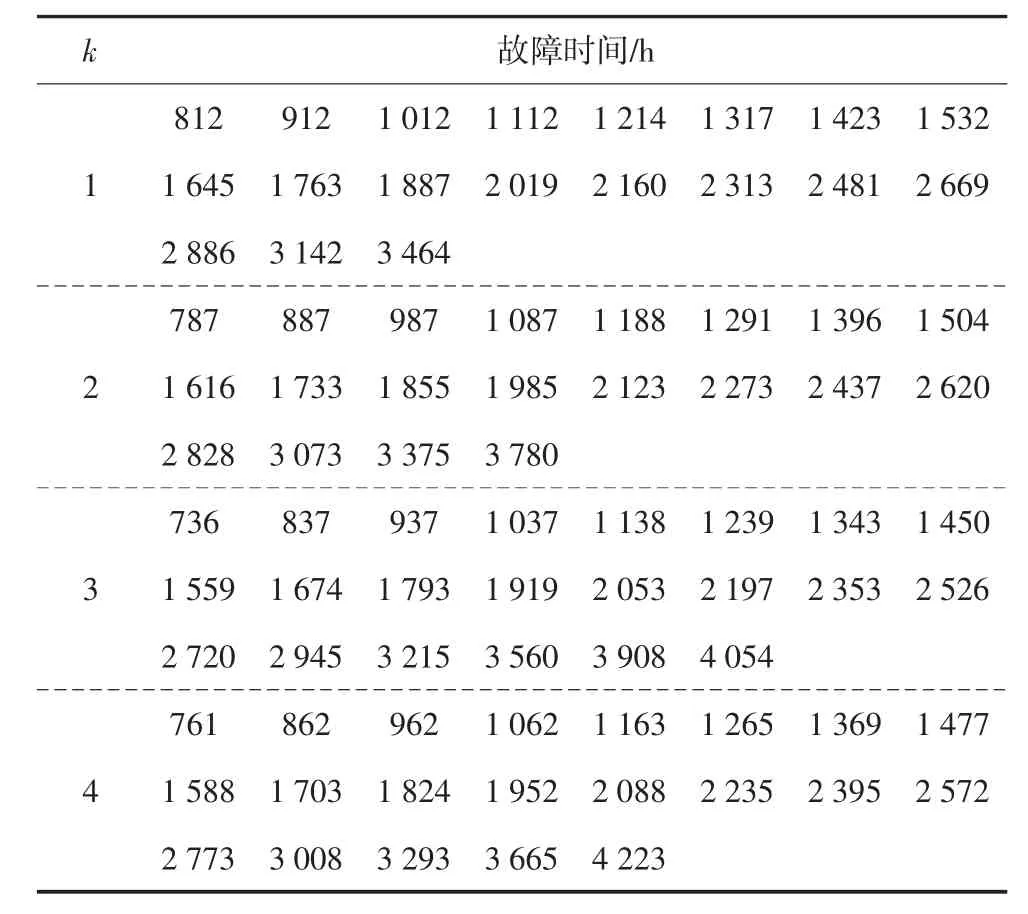
表2 元動作單元老化故障數據Tab.2 Failure data for aging failures of meta-action units

在本文中，將元動作單元用字母k 進行表示，由于在前文中將元動作單元平均分為四組，將四組元動作單元分別用1，2，3，4 進行編號，且在接下來的表格中均用此進行表示.

如前文所述，隨機故障數據用泊松分布進行擬合，老化故障數據用威布爾分布進行擬合.假設同一批次生產的數控機床性能、工作環境和工作負載均相同，那么應該用相同的參數集A=（λ0、η0、m0）對所產生的全部故障數據進行擬合.

對泊松分布進行參數估計，在本例中，沒有未發生故障的元動作單元，故tj為0：

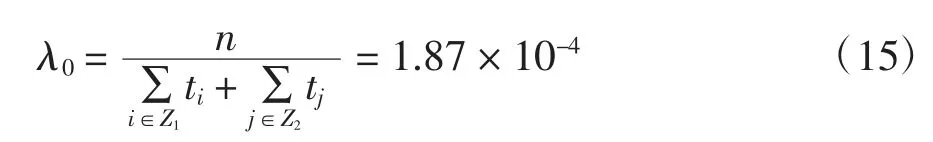
采用矩估計法對威布爾分布進行參數估計時，為保證估計的結果精確，對式（9）采用二分法進行參數估計時，方程兩端的差值應小于0.001.

對總的老化故障數據最終估計的結果為η0=2.35，m0=2 229.674

繪制老化故障數據的概率密度函數曲線f（t）和頻率直方圖，結果如圖8 所示.

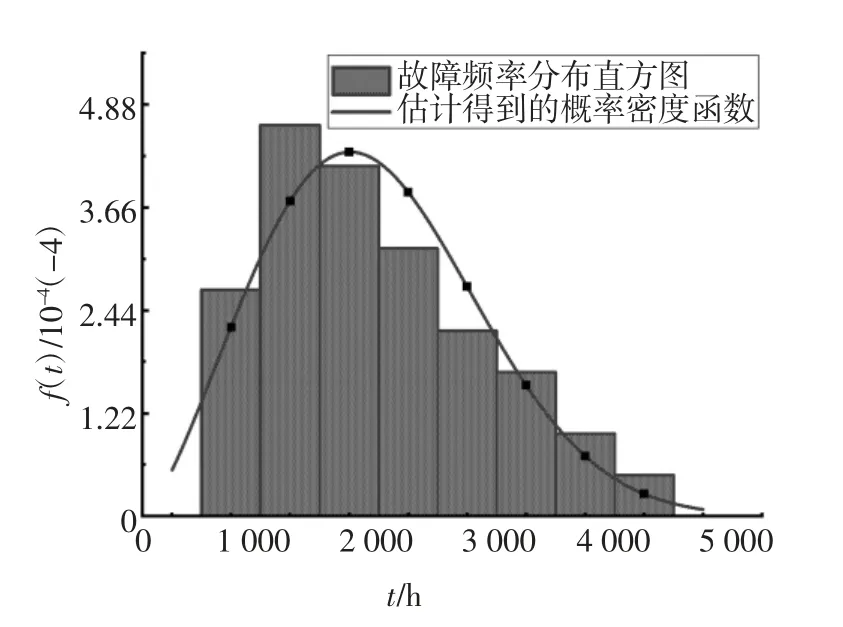
圖8 老化故障數據概率密度函數曲線和頻率直方圖Fig.8 Probability density function curve and frequency histogram of aging failure data

由圖8 可知，老化故障數據的概率密度函數曲線和頻率直方圖具有較好的擬合效果，說明威布爾分布適合用來描述老化故障數據，且提出的故障概率模型有效.

由于生產過程中各種偶然因素的影響，且所處的工作環境和工作負載各不相同，因此，對四組用戶的數控機床故障數據應該采用不同參數的概率模型來進行擬合[18].

對泊松分布進行參數估計，tj亦為0：

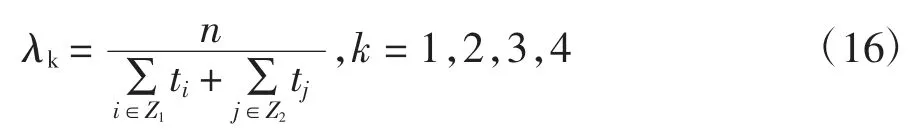
最終計算的結果如表3 所示.

表3 各組元動作單元老化故障率Tab.3 Aging failure rate of each meta-action unit

采用矩估計法對各組元動作單元故障數據進行威布爾分布參數估計，其結果如表4 所示.

表4 各組元動作單元威布爾分布參數表Tab.4 Weibull distribution parameter table of each meta-action unit

分別繪制4 組元動作單元的老化故障數據概率密度函數曲線f（t）和頻率直方圖，結果如圖9 所示.

由圖9 可知，各組元動作單元的老化故障數據概率密度函數曲線和頻率直方圖都具有較好的擬合效果，說明各組元動作單元的老化故障數據同樣適合用威布爾分布進行描述，進一步說明了提出的故障概率模型有效.

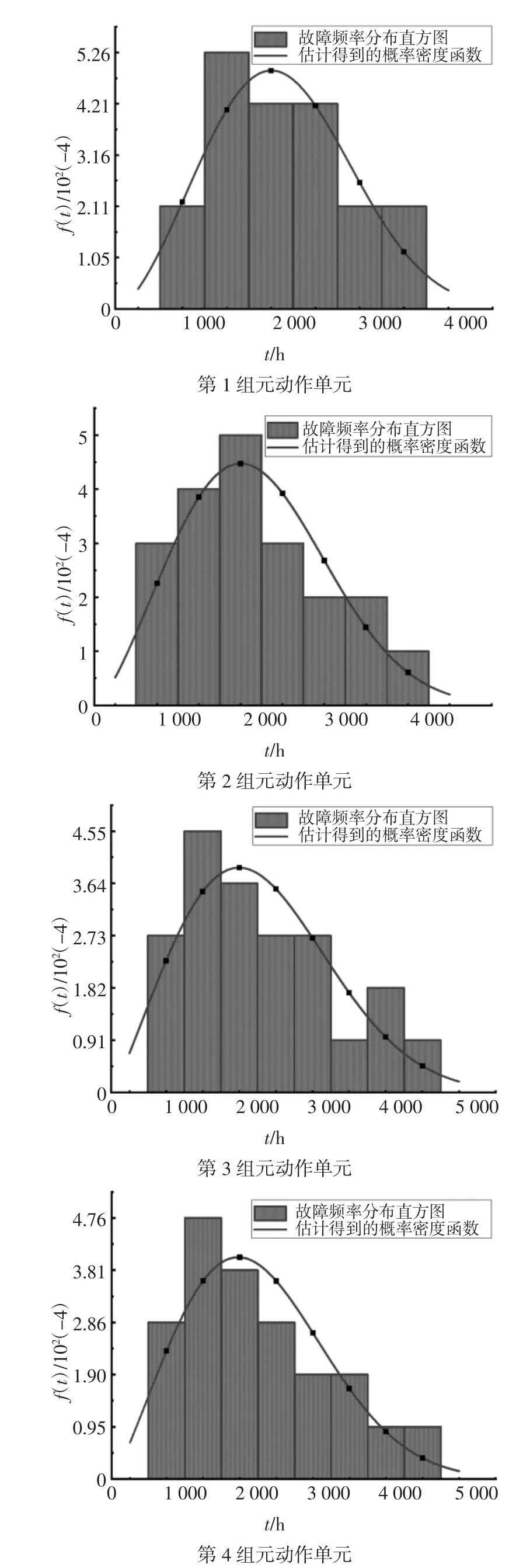
圖9 各組元動作單元老化故障數據概率密度函數曲線和頻率直方圖Fig.9 Probability density function curve and frequency histogram of aging failure data of each meta-action unit

工作負載和工作環境影響元動作單元的故障率，對于這兩個參數的估計，按圖5 所述，經計算，四組外界影響參數如表5 所示.

由表5 中的外界影響參數可知，第1 組和第2組元動作單元，工作負載小于平均水平，工作環境比平均水平更惡劣；第3 組和第4 組元動作單元則相反，工作負載大于平均水平，工作環境比平均水平更優.

表5 外界影響參數Rl 和Re 表Tab.5 External influence parameters Rl and Re

7 結論

1）本文提出了一種由威布爾分布和泊松分布組成的元動作單元故障概率模型，并考慮了工作負載和工作環境對元動作單元故障率的影響，最終發現元動作單元的故障率隨時間變化的形式類似于失去早期階段的浴盆曲線.

2）元動作單元是數控機床完成一個動作的最基本單元，其故障概率模型不僅可以對復雜機電設備的重要運動構件的可靠性分析提供幫助，還可以為運動構件維修保養計劃的制定提供依據.

3）本文提出的元動作單元故障率模型對故障數據的處理簡單，經算例分析驗證有效，并且上述的模型不僅局限于元動作單元，在可靠性領域中，故障來源可以分為老化故障和隨機故障的結構或系統均可以使用.