旋轉導向鉆具導向節軸承圓周間隙角研究*
張光偉 曹明星 程禮林 尹福來
(西安石油大學機械工程學院 陜西西安 710065)
石油資源的開采和利用是影響我國經濟發展的重要因素,石油開采技術的提高對我國經濟發展具有巨大的推動作用。旋轉導向鉆井技術是目前較先進的自動化鉆井技術,旋轉導向鉆井工具分為指向式和推靠式,其中指向式鉆井工具具有較大優越性,具有巨大的研究價值。導向鉆井工具中的軸承系統是實現導向鉆井工具旋轉導向的重要組成部分。
近年來研究人員對鉆井工具中的軸承系統作了大量研究并取得了一定成果。彭松水[1]提出了一種導向鉆井工具關節軸承的組合系統,其中包括推力關節軸承和向心關節軸承,并進行了靜力學分析和沖擊性能分析。SHI等[2]提出了一種轉軸偏轉情況下球面滾子軸承最大接觸應力的有限元計算方法,結合經典接觸力學方法及采用ANSYS軟件設計試驗過程,通過試驗驗證了分析方法的有效性。張光偉等[3-4]研究了智能型旋轉導向鉆井工具可控彎接頭的結構和工作原理,分析了導向軸、導向節和鋼球的相互作用和應力分布情況,研究表明危險區域的應力滿足赫茲理論,并提出了一種旋轉導向鉆井工具的導向節軸承。文獻[5-6]利用赫茲接觸理論對球籠式等速萬向節橢圓型溝道的接觸應力進行了研究。文獻[7-9]對萬向節軸承中滾針偏斜進行了研究,并基于赫茲接觸理論對錐齒輪的切向接觸力進行了計算。陳科等人[10]研究了虎克萬向節軸承的瞬時轉角方程,并建立軸承瞬時轉速分析的數值方法。魏維等人[11]研究了滑動軸承的間隙對潤滑油膜厚度及穩定性的影響,結果表明軸承間隙越大系統穩定性越低。文獻[12-13]研究了球籠式等速萬向節在不同轉角下的圓周間隙變化,分析了在擺角為零及不為零時圓周間隙的變化規律。文獻[14-15]研究了航空發動機整體系統中滾動軸承徑向間隙對整體振動的影響,結果表明徑向間隙增大時,接觸力較大,加速度幅值跳躍明顯,減小徑向間隙可以減小整體振動。
綜上所述,研究學者對滑動軸承間隙與潤滑油膜厚度的關系和滾動軸承徑向間隙進行了大量研究工作,但旋轉導向鉆井工具中軸承系統的結構類型多樣,對旋轉導向鉆井工具中軸承系統的偏置角、間隙等方面的研究涉及較少,而且軸承系統的工作性能對鉆井工具穩定性的影響亦鮮有報道。因此,本文作者以導向節軸承為研究對象,根據鋼球與溝道的結構特點,建立了溝道的曲面方程及數學模型;根據鋼球與溝道的幾何模型,計算了鋼球與溝道之間的圓周間隙角的大小,結果表明圓周間隙角的波動性是導致導向軸轉動過程中產生振動和噪聲的重要原因。
1 導向節軸承的結構分析
1.1 導向節軸承的結構組成
井下閉環可控彎接頭主要由旋轉外套、偏心機構、導向節軸承、導向軸、鉆頭及密封機構等組成,如圖1所示。
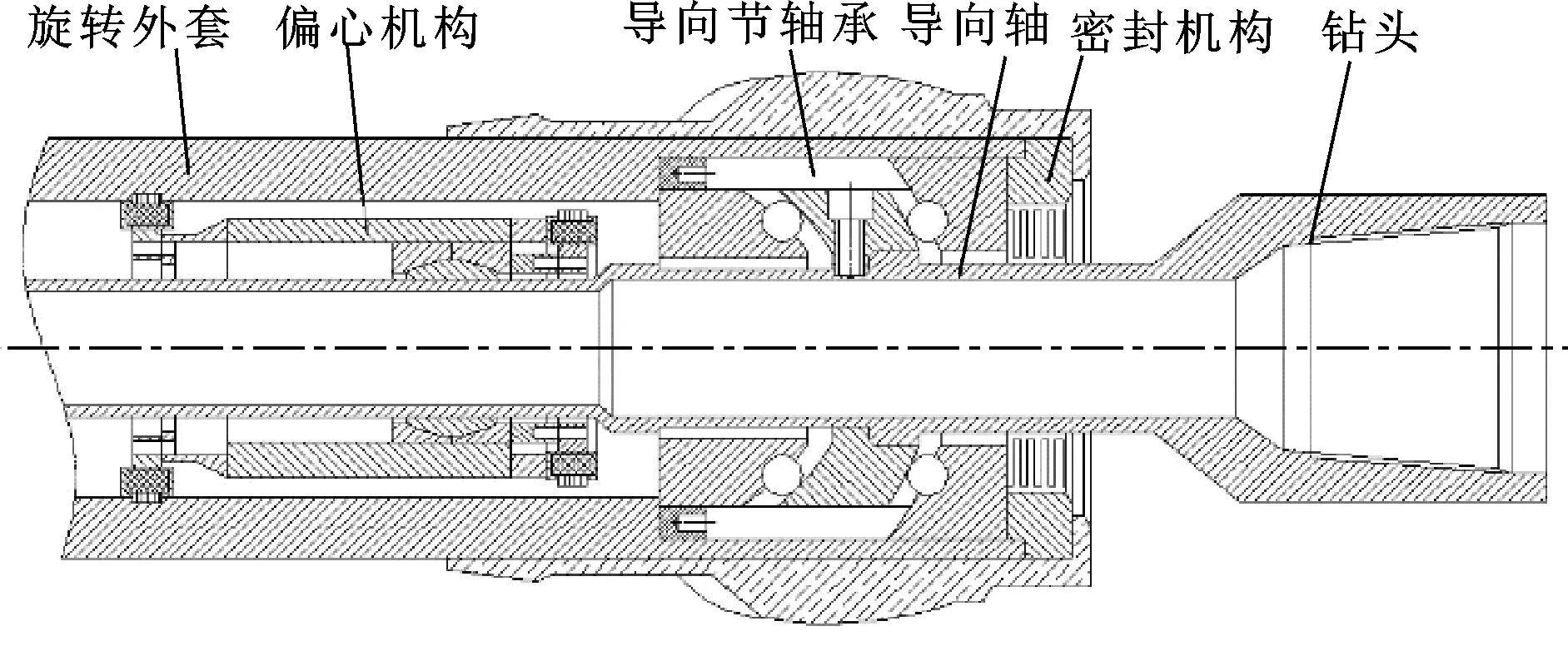
圖1 可控彎接頭結構示意Fig 1 Schematic of controlled bend sub structure
導向節軸承作為可控彎接頭中的扭矩傳遞機構,主要由球形殼、殼內鋼球、導向架、套內鋼球、球形套和導向軸等組成,如圖2所示。球形殼和球形套與旋轉外套固定連接,旋轉外套產生的扭矩直接傳遞給球形殼和球形套。導向架的兩側面為凸向一致的2個球面,球形殼內的殼內鋼球與導向架的外球面配合,球形套內的套內鋼球與導向架的內球面配合。導向節軸承中布置兩排鋼球,分別為殼內鋼球、套內鋼球;殼內鋼球沿圓周方向均勻分布在球形殼內的球窩內,球形殼和導向架通過殼內鋼球滑動配合,使二者沿徑向方向產生相對滑動;套內鋼球沿圓周方向均勻分布在球形套內的球窩內,球形套和導向架通過套內鋼球滑動配合,使二者沿徑向方向產生相對滑動。球形殼和球形套的扭矩通過鋼球與導向架球面溝道的配合傳遞給導向架,導向架與導向軸固定連接,將扭矩傳遞給導向軸,使鉆頭鉆進破巖。球形殼和球形套與導向軸之間預留有導向軸擺動的間隙,導向架與旋轉外套之間預留有導向軸擺動的間隙,偏心機構使導向軸產生偏置角,以導向節軸承為支點,實現導向軸的導向擺動功能。

圖2 導向節軸承結構示意Fig 2 Schematic of guide joint bearing structure
1.2 鋼球與溝道的結構分析
殼內鋼球和套內鋼球分別為12個,繞導向軸中心線均勻分布,且所有鋼球的大小完全相同。殼內鋼球和套內鋼球與導向架內外球面溝道的幾何簡圖如圖3所示。鋼球的球心到中心軸線的距離為R,導向架外球面溝道中心線是以軸承左端面中心S為圓心,半徑為R1的圓弧;導向架內球面溝道的中心線是以軸承左端面中心S為圓心,半徑為R2的圓弧。殼內鋼球中心為O1,套內鋼球中心為O2,O1S與軸承左端面的夾角為α1,O2S與軸承左端面的夾角為α2。
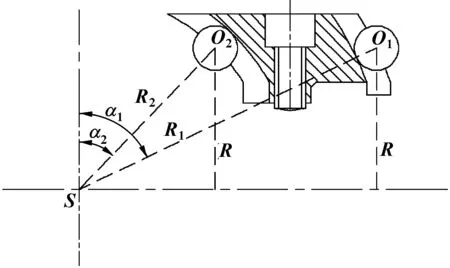
圖3 鋼球與溝道的幾何簡圖Fig 3 Geometric diagram of between thesteel ball and the channel
導向架外球面溝道為橢圓溝道,殼內鋼球與溝道的接觸面為橢圓曲面;導向架內球面溝道為橢圓溝道,套內鋼球與溝道的接觸面為橢圓曲面,由此得鋼球與球窩和溝道接觸截面,如圖4、5所示。
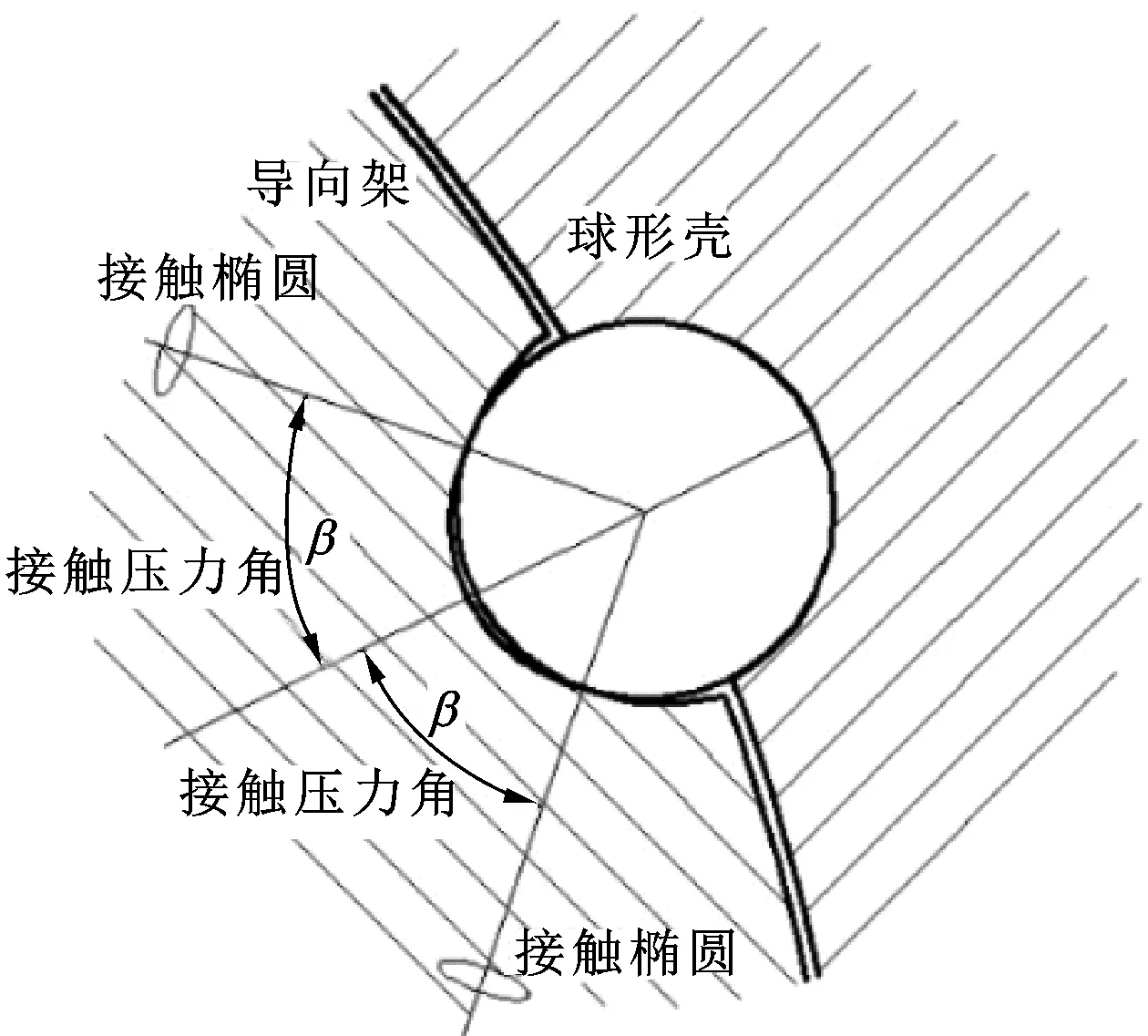
圖4 殼內鋼球與球窩和溝道接觸截面Fig 4 Contacting section of the shell ball and the channel
殼內鋼球和套內鋼球的大小完全相同,同時兩者以相同的接觸方式與橢圓溝道接觸,故對應的導向架內外溝道的橢圓截面相同,接觸性質也相同[16],由此以一個套內鋼球與對應接觸的橢圓溝道為例進行分析。在平面直角坐標系中,以橢圓中心O為坐標原點,設鋼球中心為O1,偏心距e=OO1,鋼球直徑為d,半徑為r,回轉半徑為R,如圖6所示。
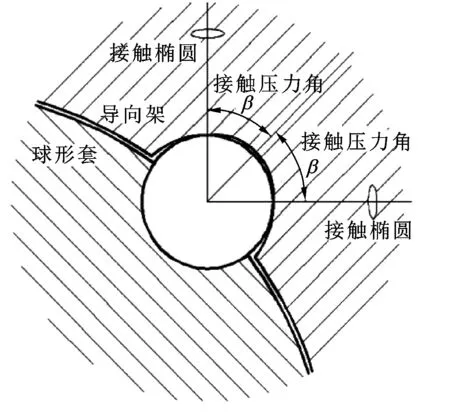
圖5 套內鋼球與球窩和溝道接觸截面Fig 5 Contacting section of the set ball and the channel
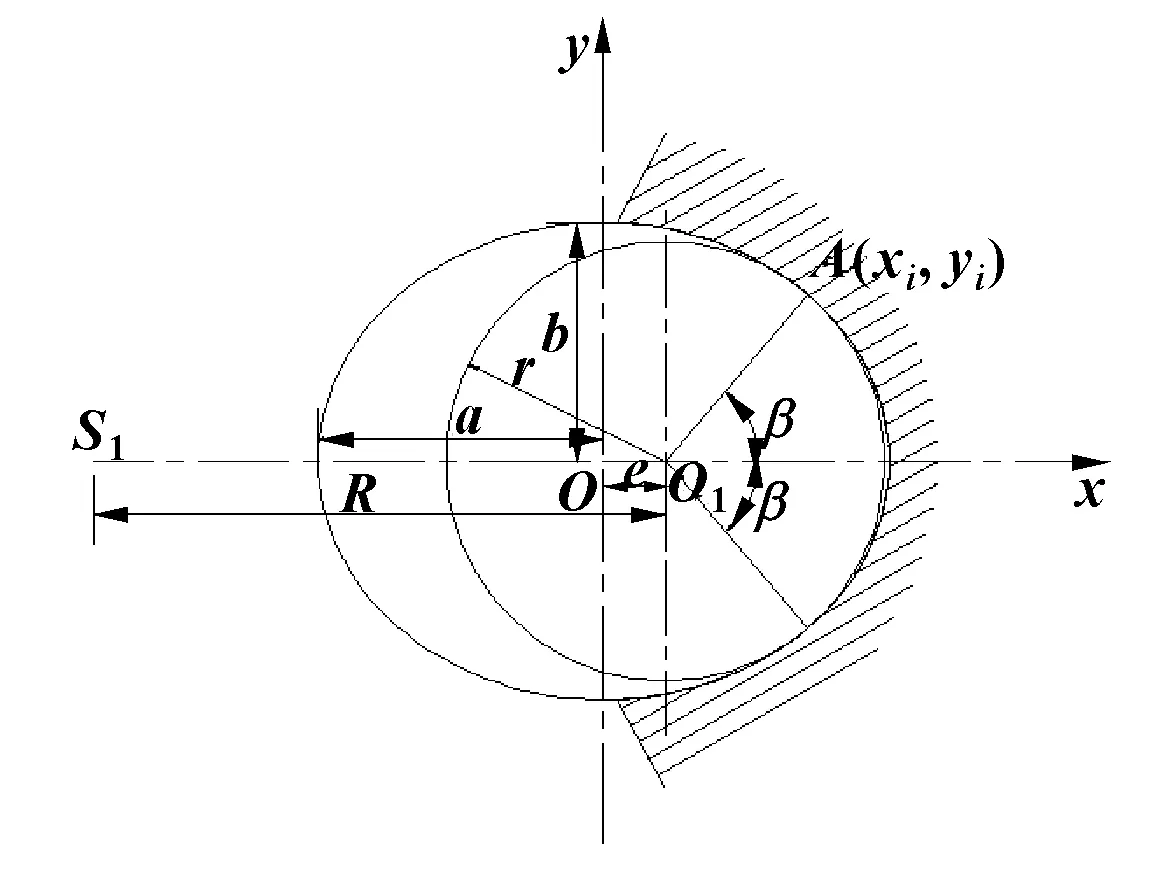
圖6 鋼球與橢圓溝道截面幾何模型Fig 6 Geometric model of the steel ball and the elliptical section
設橢圓溝道方程為
(1)
鋼球與橢圓溝道截面的接觸點A(xi,yi)在橢圓上,滿足橢圓方程,其一階、二階導數分別為
(2)
(3)
式中:ri為瞬時溝道曲率半徑,其值由公式ri=2fr求得;f為接觸點的曲率系數,通常取f=0.51~0.52[5]。
求得接觸點A(xi,yi)的坐標為
(4)
代入橢圓方程得橢圓的長、短半軸的長度分別為
(5)
根據圖6和式(4)、(5)得偏心距e為
(6)
以軸承左端面中心S為坐標原點,2個溝道上端面高為h,下端面高為h1,建立導向架內、外球面的溝道面的空間直角坐標系,如圖7所示。

圖7 空間直角坐標系Fig 7 Space rectangular coordinate system
導向架外(內)球面溝道面是由平行于xoy平面的橢圓沿xoz平面內的圓弧平移得到的。根據導向架的幾何參數,橢圓位于z=h處的平面上,橢圓面的左(右)端點距z軸的距離為x1(2),由此橢圓面的方程分別為
(x∈[-x2,-(x2-a)])
(7)
而作為橢圓平移路徑的圓弧,位于xoz平面上,其方程分別為
(8)
橢圓在平移前后橢圓的左(右)端點相對于原點形成的角度為θ1(2),平移后得到的橢圓方程分別為
(x∈[-x′2,-(x′2-a)])
(9)
根據以上方程求得導向架外球面溝道曲面的方程[6]為
4(R′1)2(x2+z2)
x∈[(x′1+a),-x1],z∈[h1,h]
(10)
導向架內球面溝道曲面的方程為
4(R′2)2(x2+z2)
x∈[-x′2,-(x2-a)],z∈[h1,h]
(11)
根據式(10)、(11)得溝道面為橢圓環面的一部分,結合鋼球及橢圓溝道的幾何參數,得到導向架外球面溝道及內球面溝道的數學模型,如圖8、9所示。

圖8 導向架外球面溝道的數學模型Fig 8 Mathematical model of guide frame outside spherical channel

圖9 導向架內球面溝道的數學模型Fig 9 Mathematical model of guide frame inside spherical channel
2 導向節軸承的圓周間隙角研究
由于潤滑要求、制造和裝配等的原因,導向節軸承中鋼球與橢圓溝道之間存在圓周間隙,若導向節軸承工作過程中間隙過大或者間隙大小不穩定會直接引起較大振動及噪聲。此外,圓周間隙將會受到偏心機構、旋轉外套等激勵的影響產生共振,從而影響軸承的可靠性和壽命。根據對導向節軸承的結構分析,殼內鋼球與套內鋼球存在的圓周間隙的計算原理是相同的。如圖10所示,以一個殼內鋼球為例,鋼球的轉動中心為O,鋼球中心為O1,鋼球半徑為r,接觸橢圓中心為E。

圖10 鋼球與溝道的剖面圖Fig 10 Profile diagram of steel ball and channel
由圖10可以得出,鋼球的截面方程為
x2+(y-l)2=r2
(12)
導向架內球面溝道截面方程為
(13)
聯立求得點K的坐標為
導向軸發生偏置時,導向軸軸線與旋轉外套軸線夾角為β,過點N1做導向軸軸線的垂線交于點I,如圖11所示。由于加工過程中存在誤差,鋼球與溝道裝配后存在間隙,設加工誤差為Δ。則|span class="emphasis_italic">KK1|=Δ/2,在△AKK1中,∠KK1A=90°,∠PKA=ω=φ1=φ2,∠K1KP=η,η為鋼球與橢圓溝道之間接觸壓力角的余角。根據實際生產情況,采用圓周間隙角θ表示該間隙的大小,圓周間隙角θ等于圓周間隙值與接觸點到導向軸軸線的距離的比值。

圖11 圓周間隙角示意Fig 11 Schematic of the circumferential clearance
套內鋼球與導向架內球面溝道之間的圓周間隙角θ為
(14)

(15)
2.1 轉角α=0°,偏置角β≠0°時的圓周間隙角
當導向軸相對于旋轉外套偏轉角度為β時,導向架外球面溝道與鋼球接觸點的位置發生偏移,但殼內鋼球與導向架外球面溝道接觸的截面形狀仍為橢圓和圓,如圖12所示。

圖12 殼內鋼球與溝道的剖面圖Fig 12 Profile diagram of shell ball and channel
同理,根據已知條件得到切點KⅠ坐標為
故
(16)
如圖11所示,過點NⅠ做NⅠI并垂直于導向軸軸線,則點NⅠ到導向軸軸線的距離為
(17)
由此可以得出,在轉角α=0°,偏置角β≠0°時殼內鋼球與導向架外球面溝道的圓周間隙角為
(18)
其中:
當導向軸相對于旋轉外套偏轉角度為β時,鋼球與球形殼溝道相切,如圖13所示。

圖13 殼內鋼球與球形殼的溝道截面Fig 13 Channel section of shell ball and spherical shell
由圖13可以看出,鋼球中心的位置坐標為
(lsinφⅠ1,lcosφⅠ1),所以
R-r=
(19)
由式(19)得殼內鋼球與球形殼溝道的圓周間隙角為
(20)
套內鋼球與導向架內球面溝道接觸截面為圓和橢圓,如圖11所示,過點NⅡ做導向軸軸線的垂線NⅡT,同理求得NⅡT為
(21)
由此可得出在轉角α=0°,偏置角β≠0°時套內鋼球與導向架內球面溝道的圓周間隙角為
(22)
其中:
套內鋼球與球形套的溝道截面如圖14所示。

圖14 套內鋼球與球形套的溝道截面Fig 14 Channel section of set ball and spherical set
鋼球的截面方程為
x2+(y-l)2=r2
(23)
球形套溝道截面方程為
x2+[y-(l-r-Δ+R)]2=R2
(24)
由圖14可看出,鋼球中心的位置坐標為(lsinφⅡ1,lcosφⅡ1),所以
R-r=
(25)
由式(25)得套內鋼球與球形套溝道的圓周間隙角為
(26)
2.2 轉角α≠0°,偏置角β≠0°時的圓周間隙角
當轉角α≠0°,偏置角β≠0°時,利用同樣的方法,點N′I到導向軸軸線的距離N′ⅠI為
(27)
由此可得,殼內鋼球與導向架外球面溝道的圓周間隙角為
(28)
其中:
當導向節軸承轉角為α時,殼內鋼球中的鋼球1的球心處于O′Ⅰ,轉動中心O變為O′,鋼球的球心位于同一平面內,如圖15所示。

圖15 球心的運動軌跡示意Fig 15 Schematic of the trajectory of ball center
根據幾何關系,計算得出:
(29)
由圖15可以看出,當導向節軸承轉角為α時,根據幾何關系,得坐標原點O與鋼球1的球心O′Ⅰ之間的距離l′為
(30)
代入式(20)得殼內鋼球與球形殼的圓周間隙角為:
(31)
因此,根據式(28)、(31)得殼內鋼球總的圓周間隙角δⅠ為
δⅠ=θⅠ2+φⅠ2
(32)
當轉角、偏置角不為0時,根據式(21),點N′Ⅱ到導向軸軸線的距離N′ⅡT為
(33)
于是可得套內鋼球與導向架內球面溝道的圓周間隙角為
(34)
其中:
如圖14所示,根據式(26)得套內鋼球與球形套的圓周間隙角為
φⅡ2=
(35)
當導向節軸承轉角、偏置角都不為0時,根據式(34)、(35)得套內鋼球總的圓周間隙角δⅡ為
δⅡ=θⅡ2+φⅡ2
(36)
3 計算分析與驗證
3.1 方法對比驗證
為了驗證文中研究方法的準確性,以文獻[12]中的參數為例,采用文中研究方法計算當旋轉一周時軸承的一個鋼球圓周間隙角大小,并與文獻[12]中分析得出的圓周間隙角的變化趨勢進行對比,如圖16所示。

圖16 鋼球圓周間隙角計算結果與文獻[12]結果對比Fig 16 Comparison of calculation results of steel ballcircumferential clearance angle with thoseof reference[12]
由圖16可以看出,采用文中研究方法計算的圓周間隙角變化趨勢與文獻[12]中結果一致,兩者變化趨勢都在0°、180°、360°出現最大值,在90°、270°的兩側出現最小波谷,從而證明了文中研究方法的準確性。
3.2 圓周間隙角的數值計算分析
根據可控彎接頭結構特點,當導向軸發生最大偏置時,通過MATLAB軟件數值計算分析,導向節軸承在旋轉一周時殼內鋼球總的圓周間隙角的大小呈周期性變化,如圖17所示。殼內鋼球中12個鋼球與溝道之間的圓周間隙角變化規律相同,鋼球2比鋼球1滯后30°,以此類推,鋼球7比鋼球1滯后180°,所以鋼球1與鋼球7的曲線重合。由圖17可以看出,鋼球1的圓周間隙角在一個周期內,出現了3次波峰和2次波谷;其中在轉角為90°時的峰值明顯較小,2個波谷剛好位于該波峰的兩側,且波峰的峰值與波谷的谷值只有10-3的差級;其他鋼球與鋼球1的波峰和波谷的數值和變化規律均相同,只是后一個鋼球的波形比前一個的波形滯后30°。
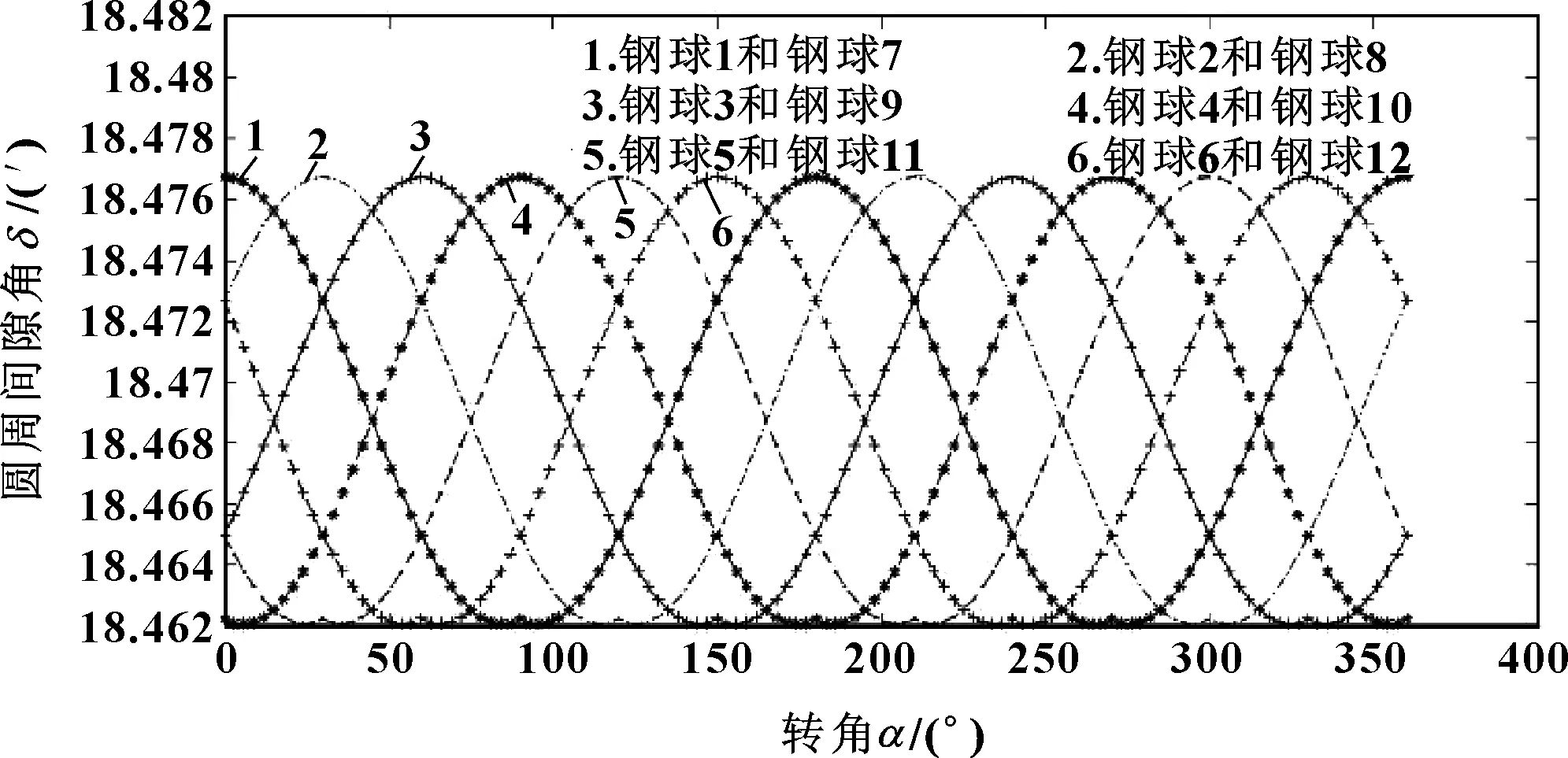
圖17 殼內鋼球總的圓周間隙角的周期性變化Fig 17 Periodic variation of shell ball’s circumferential clearance
當可控彎接頭進行導向鉆進時,導向軸的偏置角發生變化,從而使鉆頭的方向發生變化,利用MATLAB軟件的數據可視化功能,計算出了殼內鋼球總的圓周間隙角與轉角、偏置角之間的關系,如圖18所示。

圖18 殼內鋼球總的圓周間隙角與轉角、偏置角之間的關系Fig 18 The relationship between the shell ball’s clearance angleand the angles of rotational and offset
由圖18可以看出,當偏置角為0°時,不管導向軸的轉角如何變化,殼內鋼球的圓周間隙角不發生變化且為最大值;當偏置角不為0°時,鋼球的圓周間隙角隨轉角的改變呈周期性變化且周期為180°,轉角為90°、270°時圓周間隙角達到最大值與偏置角為0°時的數值相同;當轉角一定時,偏置角正負兩側的圓周間隙角是對稱的,故偏置角大小的絕對值所對應的圓周間隙角大小相同,從而得出無論導向軸朝哪個方向偏置都不影響鋼球的圓周間隙角大小。
同理,導向節軸承在旋轉一周時套內鋼球總的圓周間隙角的大小也呈周期性變化,如圖19所示。套內12個鋼球與溝道之間的圓周間隙角變化規律相同,鋼球2比鋼球1滯后30°,以此類推,鋼球7比鋼球1滯后180°,所以鋼球1與鋼球7的曲線重合。由圖19可以看出,鋼球1的圓周間隙角在一個周期內,出現了4次波峰和3次波谷;其中在轉角為90°兩側時的峰值明顯比轉角為0°、180°時的峰值小;在3個波谷中,當轉角為90°時的波谷最大,與殼內鋼球中的波峰和波谷相比,套內鋼球的波峰和波谷的差距較為明顯;其他鋼球與鋼球1的波峰和波谷的數值和變化規律均相同,只是后一個鋼球的波形比前一個的波形滯后30°。

圖19 套內鋼球總的圓周間隙角的周期性變化Fig 19 Periodic variation of set ball’s circumferential clearance
當轉角、偏置角同時發生變化時,利用MATLAB軟件的數據可視化功能,計算出了套內鋼球總的圓周間隙角與轉角、偏置角之間的關系,如圖20所示。

圖20 套內鋼球總的圓周間隙角與轉角、偏置角之間的關系Fig 20 The relationship between the set ball’s clearance angleand the angles of rotational and offset
由圖20可以看出,當偏置角為0°時,不管導向軸的轉角如何變化,套內鋼球的圓周間隙角不發生變化且為最大值;當偏置角不為0°時,鋼球的圓周間隙角隨轉角的改變呈周期性變化且周期為180°,轉角為90°、270°時圓周間隙角達到最大值與偏置角為0°時的數值相同;當轉角一定時,偏置角正負兩側的圓周間隙角是對稱的,故偏置角大小的絕對值所對應的圓周間隙角大小相同,從而得出無論導向軸朝哪個方向偏置都不影響鋼球的圓周間隙角大小;與殼內鋼球圓周間隙角變化規律是相同的。
4 結論
(1)根據導向節軸承的結構組成,分析了導向節軸承的運動原理;根據鋼球與溝道的接觸特點,計算出了橢圓溝道截面的幾何方程和溝道面的曲面方程,建立了導向架外、內球面溝道的數學模型。
(2)當導向軸偏置一定角度時,鋼球與橢圓溝道之間的圓周間隙角隨轉角的增大呈周期性變化,每排鋼球的變化規律相同且具有波動性;利用MATLAB軟件進行數值計算,得出了套內鋼球總的圓周間隙角比殼內鋼球總的圓周間隙角波動性大。
(3)根據鋼球總的圓周間隙角與轉角、偏置角之間的關系曲線,得出了導向軸偏置角為0°時,鋼球總的圓周間隙角恒定不變且最大;在偏置角不為0°時,鋼球總的圓周間隙角呈現出的波動,其中套內鋼球總的圓周間隙角比殼內鋼球總的圓周間隙角波動性大,是導致導向軸轉動過程中產生振動和噪聲的重要原因。

