無人機輔助的移動邊緣計算中的任務分配策略
王岱巍,徐高潮,李 龍
(吉林大學計算機科學與技術學院,長春 130012)
0 引言
隨著物聯網(Internet of Things,IoT)的普及以及移動應用程序功能的日漸強大,用戶設備(User Equipment,UE)的計算需求已達到前所未有的水平。移動邊緣計算(Mobile Edge Computing,MEC)技術由于可以在較小的延遲下為資源受限的UE提供處理計算密集型任務的能力,受到學術界和業界的日益關注。標準化組織和行業協會如歐洲電信標準化協會(European Telecommunications Standards Institute,ETSI)和5G汽車聯盟(5G Automotive Association,5GAA)已經確定了MEC 的幾個應用場景,主要有智能視頻加速、可感知應用程序的性能優化、萬物互聯、大規模機械化通信等[1-2]。MEC 的基本原理是通過在接入點(Access Point,AP)部署云服務器,使UE 的計算任務可以在無線網絡的邊緣完成,從而將UE 從繁重的計算工作任務中解放出來并延長其電池壽命[3-4]。
當前對于MEC 的應用中,提高系統能效或減少各種基于蜂窩網絡的MEC 系統的等待時間的相關研究主要有文獻[5-10]。文獻[5]中研究了多輸入多輸出(Multiple Input Multiple Output,MIMO)的MEC 系統,通過聯合優化通信功耗和計算資源將總能耗降至最低;文獻[6]中研究了具有邊緣云和中心云并存的兩層異構網絡,并且對計算卸載的目標選擇進行了優化以最大限度地減少網絡通信的能耗;文獻[7-10]中考慮將無線電力傳輸(Wireless Powered Transmission,WPT)技術應用到MEC 系統中,這使UE 能夠為其無線通信和本地計算提供可持續的能量供應,但增加了系統的復雜度。
此外,由于無人機(Unmanned Aerial Vehicle,UAV)在通信方面的諸多優勢如按需部署、快速部署、視距通信等[11],使用UAV協助的MEC服務有著巨大的前景。對此,有諸多側重點不同的相關研究。在文獻[12]中,對于UAV輔助的MEC系統,使用一種兩階段交替優化的方法,獲得了使能量效率最大化的飛行軌跡與通信和計算資源的分配;在文獻[13]中,研究了啟用WPT 技術的支持UAV 的MEC 系統,其中UAV 可以提供能量發送和MEC 服務,以便為UE 供能以及計算卸載。通過交替算法,解決了在局部和二進制泛洪模式下的計算速率最大化問題。在另一項研究[14]中,UAV 作為UE 而不是MEC服務器,由多個蜂窩地面基站提供服務以計算UAV 產生的任務。通過連續凸逼近(Successive Convex Approximation,SCA)算法,優化了資源分配策略和UAV 軌跡,使UAV 的任務完成時間最小化。此外,在文獻[15]中,考慮將多架UAV 以固定的飛行軌跡作為邊緣服務器為一定范圍內的UE提供服務,通過使用強化學習解決混合整數非線性規劃的方法,使UE的能耗最小化。
盡管應用廣泛,但限制UAV 在移動邊緣計算中廣泛應用的最主要原因在于,UAV 使用電池供能,其保持飛行狀態的時間和機載計算設備的計算能力都是有限的。為此,文獻[16-18]中的研究主要針對UAV 的能耗進行優化:文獻[16]中研究了基于UAV 的MEC 系統,在此模型中UAV 可以提供計算能力,幫助UE 計算其任務,通過使用SCA 方法共同優化任務分配和UAV 的軌跡,將UAV 的總能量消耗降至最低;文獻[17]中分別考慮了UAV 和UE 兩者各自的能耗,并基于不同的帕累托最優權衡得出了不同的軌跡與通信功率;文獻[18]中通過推導出旋翼UAV 的能耗計算公式,使用SCA 聯合優化了飛行軌跡與通信策略,解決了旋翼無人機的能量最小化問題。
此外,如果UE分布比較分散,單次飛行很難對于全部UE實現訪問覆蓋,因此可能需要多次派遣UAV 來完成全部覆蓋或者派遣多架UAV 共同工作,因此,減少派遣次數或派遣數量,將有效地降低收集全部數據所需的時間或成本。為此,考慮在派遣UAV完成任務之前,對終端和UAV進行預分配。通過多次飛行遍歷多個聚類中的終端,UAV 可以完成大規模的訪問與通信任務。為此,可以考慮使用聚類算法對地面UE進行劃分,從而將大規模的任務分成多個子任務來執行。在文獻[19]中,使用了自組織特征映射(Self-Organizing feature Map,SOM)網絡對用戶進行實時聚類,該聚類以信道增益作為判斷類別的指標,得到了UAV 的最佳部署位置;在文獻[20]中,提出了一種基于最小包圍圓和改進K均值聚類算法(K-means clustering algorithm)的無人機基站優化部署方法,解決了無人機基站在無線通信中的位置部署和軌跡優化問題。當前基于歐氏距離的聚類方法主要有K-Means 算法及其衍生的改進算法、迭代自組織數據分析(Iterative Self-Organizing DATA analysis,ISODATA)方法等,對于K-Means 算法和類似的改進算法,聚類數目需要預先確定,而在本文場景下,不同的地面節點分布、不同的數據傳輸量,都會導致最佳的聚類數目不同,因此難以預先確定;對于自適應的ISODATA 算法,其諸多的初始參數在本文場景下也難以確定。
在此背景下,本文設計了一種適用于UE大范圍分布的場景下使用UAV 對計算卸載數據進行收集的解決方案。首先,運用現有的對于旋翼UAV 的功率計算函數及無線通信的能耗函數推導出本文描述場景中的能量消耗函數,并將問題設定為在多個約束條件下該函數的最小化,該問題需要優化UAV 的飛行軌跡、飛行速率以及UAV 的通信策略,是一個非凸的問題;之后,通過使用連續凸逼近方法,可以將原非凸問題轉化為迭代求解凸優化的問題,在每次迭代時同時更新UAV 軌跡和通信時間分配;最后,可以收斂到一個滿足原問題KKT(Karush-Kuhn-Tucker)條件的解。
在獲取了能耗最小化的策略后,進一步設計了一個自適應的聚類方法,通過多次迭代進行分裂與合并,獲得合適的聚類策略,以保證每個聚類簇中所有的UE都可以在一次飛行中訪問,且聚類的數量盡可能地少,從而減少UAV 的起飛次數以提高覆蓋效率,或減少UAV 的派遣數量(對于多UAV 訪問多個聚類的場景)以降低覆蓋成本。
1 系統模型及問題描述
1.1 系統模型
如圖1 所示,考慮一種UAV 輔助的移動邊緣計算下的數據收集場景。
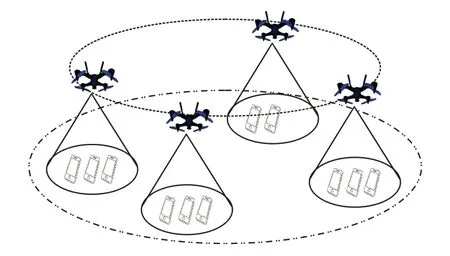
圖1 無人機協助的移動邊緣計算系統Fig.1 UAV-assisted MEC system
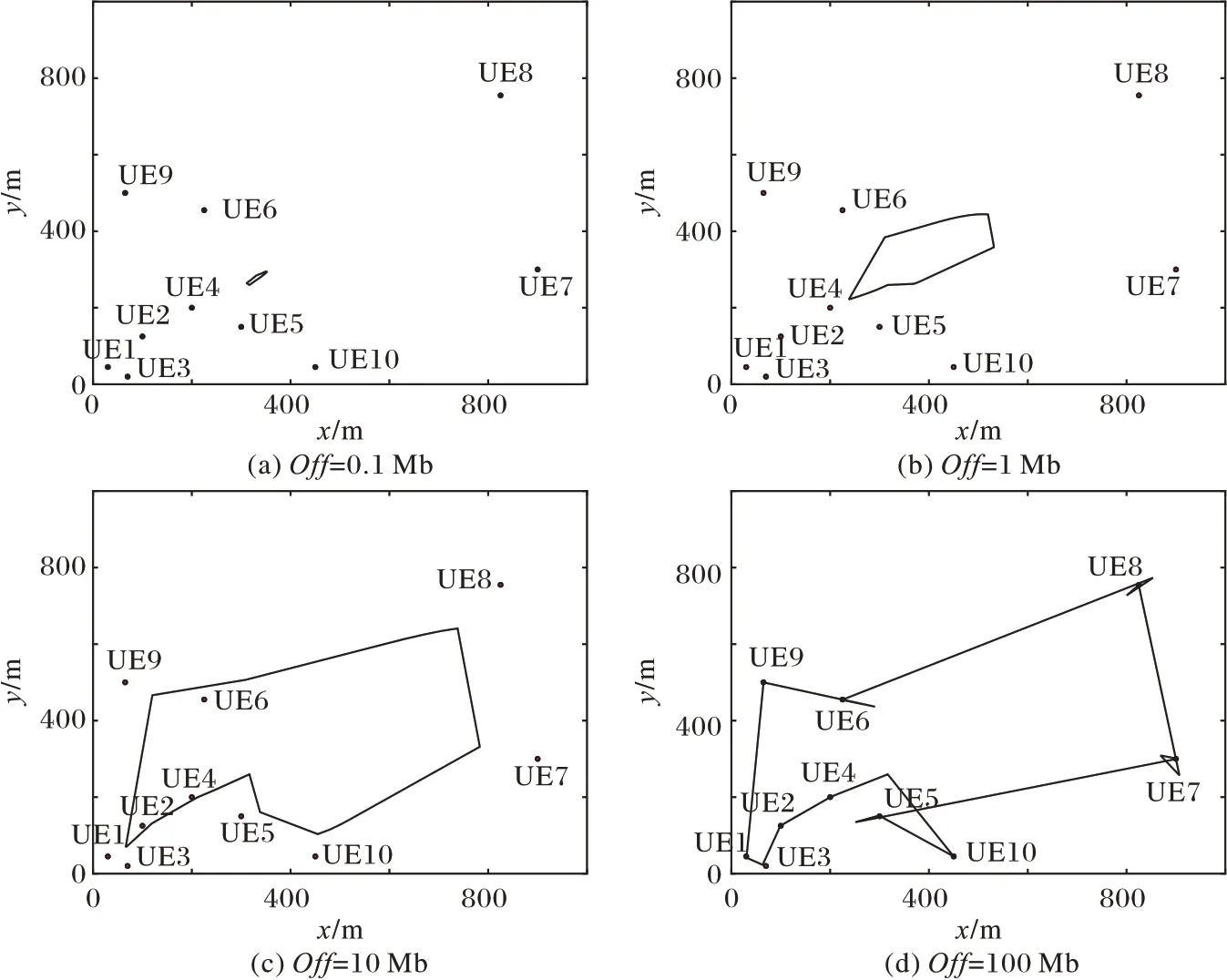
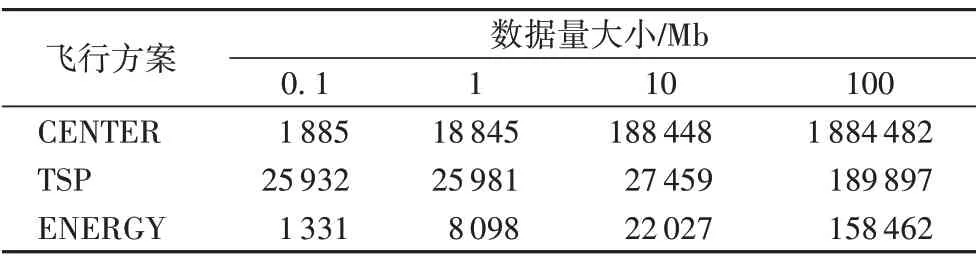
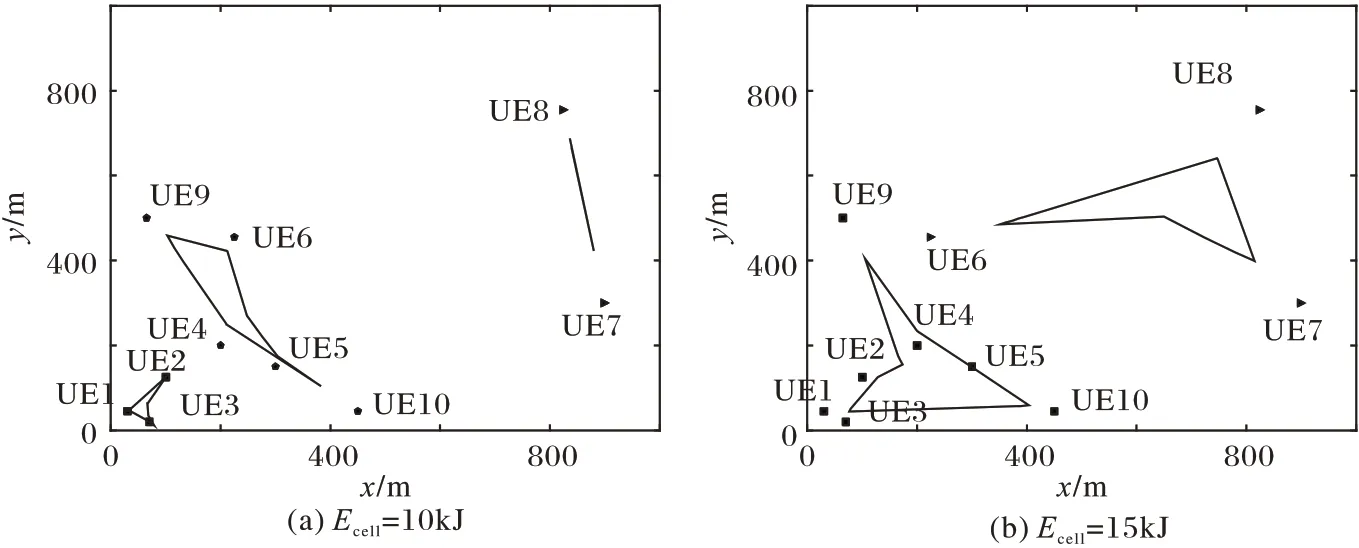
在此場景下,在地面上有N個UE,表示為集合N={1,2,…,N},對于序號為n的UE(n∈N),其位置在三維坐標系中表示為wn={xn,yn,0},并有Offn大小的計算卸載數據需要上傳到邊緣服務器上。UAV 在此場景下作為移動邊緣服務器的數據收集器,對全部UE的計算卸載數據進行接收。將UAV 接收全部UE 數據的總時間表示為Tt,設UAV 的飛行高度恒定為H,其在t時刻的位置表示為loc(t)=(xt,yt,H),0 其中β0表示距離為1 m 時的信道功率增益。根據香農公式,UAV與第n個UE之間的傳輸速率Rn(t)可以表示為: 其中:B為信道帶寬;P為UE 的通信功率;σ2表示噪聲功率,表示單位距離為1 m 時的信噪比;將第n個UE在t時刻的通信狀態表示為Sn(t),當等于1 時表示第n個UE在t時刻與UAV 通信,0表示不通信。由于在TDMA 接入方式下UAV 在某個時刻t只能與1 個UE 通信,因此可以得到以下約束: 因此,在總的飛行時間里,UAV 與第n個UE 之間的傳輸數據量DATAn可以表示為: 由于UAV 需要收集所有UE 的數據,對于DATAn有以下約束: 由文獻[18]中的研究可以得到,旋翼UAV 的飛行功率與速度之間的關系為: 其中各個參數的具體含義如表1所示。 表1 UAV相關參數Tab.1 UAV related parameters 當速度為0 時,懸停功率可以表示為P0+Pi,由式(6),UAV在其飛行總時間內的能耗可以表示為: 其中v(t)=。對于UAV 的通信能耗,設其在t時刻的通信功率為Pcomm(t),因此,UAV 在飛行期間的通信能耗可以表示為: 考慮到UAV的最大通信功率為Pc,則有以下約束: 因此,UAV的總飛行能耗可以表示為: 由于UAV 板載電池的儲存電能有限,在大傳輸量或大分布范圍的場景下,單機單次飛行無法收集全部的計算卸載數據,需要派遣多架UAV同時執行任務或單架UAV多次起降執行任務。為此,將UAV 執行的任務分成c個獨立的子任務,對于每個子任務taski(i∈[1,2,…,c]),將會在一次飛行中完成對于若干個UE進行計算卸載數據的收集。將地面上的UE作為樣本,將UAV 需要執行的子任務數量c作為聚類數目,就可將問題轉化為將地面的N個樣本劃分成c個聚類的問題。 首先,用Γi(i∈[1,2,…,c])表示第i個聚類,其中的樣本數表示為ki,則需要滿足約束: 此外,用Ei(i∈[1,2,…,c])表示UAV 收集聚類Γi中全部樣本所消耗的最小能量,將UAV 板載電池儲存的能量表示為Ecell,則需滿足以下約束: 基于以上討論,減少聚類的數量,將會減少派遣UAV 的成本,為此就需要UAV 以盡可能節能的策略飛行,從而可以在一次飛行中盡可能遍歷更多的UE,因此,問題被分為能耗最小化和聚類數量最小化兩個問題。 對于能耗最小化問題,可以公式化表示為P1: 對于約束(18),由于UAV 使用場景的局限性,通常難以在任意位置起降,因此在本文模型中,考慮將起飛和降落點都設為同一個點loccenter。 對于聚類數量最小化問題,可以公式化表述為P2: 由于在P2 的約束(12)中,Ei的計算依賴于對P1 的求解,因此,接下來的工作首先解決P1,得到一個計算Ei通用的方法,再根據此方法解決P2。 由于問題P1是建立在連續時間變量上的,需要優化的變量也是無限多的,無法有效求解,因此需要將其轉化為有限個變量的優化問題。首先將其飛行軌跡loc(t)轉化成有限個,將其細分成M個線段。在此,M的取值要足夠大,使每一個線段m的長度足夠小,以使在每一個線段m∈[0,1,…,M-1]中,UAV 與各個UE 間的距離以及通信功率均可視為不變,從而可以將UAV 的軌跡近似視為M個固定的坐標點組成的集合。為此,需要M+1個點來將路徑離散化,將這些點表示為集合{locm},m∈[0,1,…,M],其中,loc0=locM=loccenter,UAV 執行任務的時間Tt也可以離散化為M個時間片段{Tm},m∈[0,1,…,M-1],Tm表示在線段m上的飛行時間。由于UAV 有飛行速度上限Vmax,在任意一個線段m上的飛行速度都不可能大于Vmax,因此可以將P1的約束(14)改寫為: 將路徑離散化后,UAV 與第n個UE的距離不再是一個連續函數,而是M個表達式的集合。 將UAV 在線段m上飛行時與第n個UE 的通信時間表示為τmn,則需新增約束: 通信功率Pcomm(t)也可以離散化表示為Pm,m∈[0,1,…,M-1],從而可以將約束(17)改寫為: 對于P1中起飛和降落點的約束(18),同樣可以改寫為: 用Δm=‖locm+1-locm‖,m∈[0,1,…,M-1]來表示線段m的長度,則UAV 在線段m上的平均飛行速度vm可以轉化成Δm/Tm。將上述生成的離散化變量集合帶入P1 的目標函數中,可以將原目標函數改寫為: 最終,可以將P1轉化為有限變量的優化問題P3,表示為: P3 仍然是一個非凸問題,因為目標函數E({locm},{Tm},{τmn},{Pm})以及約束(22)都是非凸的,難以直接求解,因此需要對其進行轉化。首先,對于目標函數的第一個非凸項,考慮到UAV 的主要能耗是保持飛行狀態所需的機械能耗,其通信能耗相對而言很小。因此,雖然減小通信功率可以降低一部分通信能耗,但是也會導致接收速率變低,從而使UAV 收集同樣大小數據的時間變長,為此UAV 需要額外的懸停或飛行時間來完成任務,由此導致的額外機械能耗遠大于節省的通信能耗。因此,想要最小化UAV 的飛行能耗,就必須將網卡的通信功率保持為UAV 所能提供的最大通信功率Pc以保持最大的數據接收速度。因此,可將其轉化為凸表達式,并將約束(23)省略。 此外,對于非凸約束(22),引入第二個松弛變量集合{ψmn},將其表示為: 從而可以將式(22)改寫為: 通過代換,可將松弛變量ψmn與原變量的關系表示為: 由定理1,問題P3可以轉化為等價問題P4: 定理1P3和P4等價。 證明 P3 與P4 的差別在于P4 中將松弛變量與原變量的關系表達式(27)、(30)變成了不等式約束(32)、(31),若P4 有一個解使約束(32)滿足嚴格不等條件,那么若不斷減小松弛變量φm,直到使約束(32)滿足嚴格相等條件,目標函數E也會隨之逐漸減小,因此,此解一定不是P4 的最優解,對于約束(31)同理。因此P4 的最優解一定可以使約束(31)和(32)滿足嚴格相等條件,此時的目標函數與約束都與P3 相同,因此P3與P4等價。證畢。 由于非凸約束(29),(31)和(32)的限制,P4 仍然非凸,然而,這3 個約束中的非凸表達式都可以通過替換獲取其在某個局部解的全局下界,從而將非凸表達式轉化為凸。對于約束(29),由于凸函數的一階泰勒展開式可以視為凸函數的全局下界,可以將凸表達式在局部點處展開,獲取其在的全局下界,表示為不等式: 對于約束(31)中不等式右側的表達式,雖然因為非凸不能使用一階泰勒公式的性質,但可以由定理2 獲取其全局下界,定理2表示如下: 證明 見文獻[21]中的定理2。 最終,將P4 中約束(29)、(31)和(32)中相關表達式替換為在局部點的全局下界表達式(33)、(35)和(34),可以將P4轉化為P5: P5 在轉化后變成了一個凸問題,可以使用相關的工具包進行求解。在算法1 中,通過將P5 中的局部點逐步逼近到使目標函數值更小的點,可以使每一輪迭代產生的局部最優值逐漸趨近全局最優值。當兩輪迭代求得最優值的比值大于給定閾值ε時,算法收斂,獲得的解可以視為原問題P3的近似最優解。算法1如下。 算法1 基于SCA的迭代算法。 算法的收斂性由定理3可知。 定理3算法1 每輪迭代的最優值單調遞減且計算出的最優解滿足原問題P4的KKT條件。 證明 為方便起見,將P4 和P5 中的變量簡單表示為x,將P4 中的約束表示為fi(x) ≥0,?i∈[1,2,…,I],將算法1 中第j輪迭代計算P5時的全部約束表示為gi,j(x) ≥0,?j、?i∈[1,2,…,I]。 首先,由于在算法1中,第j輪迭代求解P5時的全部約束,一部分是將P4中的約束改寫成了在某個局部點的全局下界,另一部分為原約束,因此可以滿足gi(x) ≤fi(x)。 由于滿足以上3 個條件,根據文獻[22]中的命題3 可知,算法1 最終迭代產生的解可以視為原問題P4 的近似最優解,且在此最優解下的各項最優值均滿足原問題P4的KKT條件。證畢。 通過第2 章提出的能量最小化算法,可以在給定地面UE分布和數據傳輸量要求時,獲取使UAV 能耗最小的飛行軌跡、飛行速度以及與各個UE之間的通信時間。接下來據此對地面上的終端進行聚類,以減少飛行的次數或派遣UAV 的數量。為此,設計了一個以飛行能耗為聚類標準的自適應聚類算法來解決P2,其具體步驟如算法2所示。 算法2 基于分裂與合并的自適應聚類算法。 步驟1 將地面的N個UE表示為樣本集{w1,w2,…,wN},c為聚類的數量,Ui(i=1,2,…,c)為初始的聚類中心。在算法開始時,令c=1,隨機選取一個點Um作為聚類中心。 步驟2 按照以下關系 若‖w-Ui‖≤‖w-Uj‖;i,j=1,2,…,c且i≠j,則w∈Γi 將樣本分到各個聚類中去; 步驟3 按照以下關系 更新聚類中心Ui的位置,其中Ni是第i個聚類的樣本數目,wk為聚類Γi中的第k個樣本點。 步驟4 將Ui作為UAV 起飛和降落的地點loccenter,將聚類中的樣本作為此次飛行需要完成數據收集的UE集合,通過算法1計算其總能耗Ei。 步驟5 對于每一個聚類Γi(i=1,2,…,c),判斷其總能耗Ei是否小于UAV機載能量Ecell,對于滿足能耗限制的聚類,將此聚類的樣本點及其總能耗Ei保存;對于超出機載能耗的聚類Γj,進入步驟6;當本步驟保存的全部聚類均滿足能量約束時,進入步驟9。 步驟6 計算當前不滿足能量約束的聚類Γj的標準差向量σj=[σjx,σjy]T,其中: 步驟12 計算以Unew為loccenter,以Γnew中的全部樣本作為需要完成計算卸載任務的UE 集合產生的能耗Enew,若Enew≤Ecell,則刪除生成Γnew的兩個原聚類,并使Γnew生效,令c=c-1,回到步驟9;如果Enew>Ecell,說明不可合并,回到步驟10,從之前保存的位置向后繼續搜索。 算法2的整體流程如圖2所示。 圖2 算法2的流程Fig.2 Flowchart of algorithm 2 進入步驟9 之前,算法通過不斷的分裂,將樣本分成多個滿足能量約束的聚類。由于某些特殊情況如樣本存在離群點,在步驟7 中通過標準差選擇的新聚類中心不合適等,分裂出的某些聚類內樣本非常少,因此在步驟9~12將會嘗試對分裂完成后的聚類進行合并。在步驟10 中,以聚類之間的距離Dij作為合并的優先級,Dij越小,優先級越高。由于當兩個聚類各自的能量消耗之和大于Ecell時,合并出的新聚類將需要更多的能耗來完成數據收集任務,因此只有當兩個聚類能量消耗之和小于機載能量Ecell時,才會嘗試進行合并。在步驟12 中,一旦完成了合并,之前使用的遞增距離序列{Dij}將會失效,因此將返回步驟9 重新生成新的序列。若不能合并,則返回步驟10 繼續向后搜索下一個有合并可能的兩個聚類。當步驟10 遍歷完{Dij}時,所有可能的合并操作已全部完成,算法結束。 為驗證所提出的能耗最小化算法和聚類算法的效果,設計了4個仿真實驗,首先,在一個給定的UE 分布條件下,通過計算本文提出的能量最小化算法在不同卸載數據量下對應的飛行軌跡來獲取結果,并分析其合理性。接著,設計了幾種不同的飛行軌跡方案來驗證本文設計的算法在能耗方面的優化。之后,為了呈現聚類算法的效果,在給定UE 的分布條件和各自的計算卸載數據量大小的情況下,將UAV 機載電池的能量作為變量,在固定的數據卸載量下獲取相應的聚類結果。最后,在本文描述的應用場景下,使用一種遞增聚類中心數目的K-Means 聚類算法與本文提出的聚類算法進行對比,來驗證本文提出的聚類算法的高效性和普適性。 仿真實驗運行在使用Intel Core i7 8750H 處理器,主頻為3.9 GHz,內存為16 GB,操作系統為Ubuntu16.04 的計算機上,仿真程序代碼使用Python2.7 編寫。對于優化模塊,使用解決非線性優化問題的方法包PyOpt[23]來求解,使用的優化器有SLSQP、ALGENCAN、NSGA2。 首先,對于UAV 相關參數,設UAV 重量W=20 N,空氣密度ρ=1.225 kg/m3,螺旋槳半徑R=0.4 m,螺旋槳梢速Utip=120 m/s,螺旋槳轉盤面積A=0.503 m2,懸停時轉子的感應速率v0==4.03,螺旋槳葉片功率P0=79.856 W,感應功率Pi=88.628 W,網卡最大通信功率Pc=5.0 W,螺旋槳在轉盤中的面積占比s=5%,UAV 的最大飛行速度Vmax=30.0 m/s。 此外,對于能耗最小化模塊,設置信道帶寬B=1MHz,UAV 的飛行高度H固定為100 m,噪聲功率σ2=-110 dBm,UE 的通信功率P為10 dBm,信道功率β0=-50 dB,由此可以計算出γ0=70 dB。 在算法1中,需要生成初始的軌跡集合、UAV 在每條線段m上的飛行時間集合以及在線段m上與第n個UE 的通信時間集合。在此,為了生成一個合理的初始值集合,使用動態規劃(Dynamic Programming,DP)求解旅行商問題(Traveling Salesman Problem,TSP)的方式,計算出以聚類中心為起點和終點,連接所有樣本點的最短路徑。然后將這條最短路徑離散化為M+1個點作為。之后計算出在此下可以滿足P3 約束的最小時間Tˉ作為集合中的每一項,并令τmn=作為的每一項,生成的結果作為算法1的初始值。實驗設置了10個UE的位置,并將M設為30,以平衡精確度和算法的運行時間。將全部N個UE 的計算卸載任務量Offn統一為同一個值,表示為Off,以方便算法的實現。 對于聚類模塊,由于在特定場景下,某個聚類中可能只含有一個樣本,而通過聚類算法計算的聚類中心位置,即起飛和降落點,也為此UE 的位置,因此,在實驗中,設UAV 訪問只有一個UE 的聚類時,飛行速度為0,在UE 的上方懸停,因此其產生的能耗僅與UE 的計算卸載任務量Offn有關。此外,設置聚類分裂時的分裂系數q=0.8。 首先,10 個UE 的位置如圖3 中所示,分別將數據傳輸量Off設置為0.1 Mb、1 Mb、10 Mb、100 Mb,使用所提出的能量最小化方案,獲得的軌跡如圖3所示。 圖3 四種數據傳輸量下的飛行軌跡對比Fig.3 Flight trajectories comparison under four data transmission amounts 由圖3(a)可知,當吞吐量較小時,UAV 趨近于以一個半徑較小的接近環形的軌跡飛行,而不會向UE 的方向顯著偏移,這可以理解為當傳輸量小時,雖然UAV 以此軌跡飛行會導致自身與UE 的距離較遠,傳輸速率較低,但是由于數據量很小,傳輸速率降低導致的通信時間增加所產生的額外能耗并不如飛行時向UE偏向而產生的機械能耗大;當數據量足夠大時,從圖3(d)中可以看出,UAV 趨近于在每一個UE 上方盤旋和懸停來與UE 通信,這也可以理解為由于數據量大,需要傳輸速率更快,這樣減少了總通信時間也就減少了飛行和懸停的時間,而由此節省的能量要大于向UE偏向所產生的額外機械能耗。當吞吐量在一個適中的大小時,如圖3(b)、(c)所示,UAV 的軌跡會向UE 的位置偏移但不會飛至UE 的上方,這是優化算法在飛行能耗和通信時間之間做出的權衡。 接下來,為了體現本文方案在能量上的優化效果,本文額外設計了兩種使用固定軌跡的方案作為對比:第一種將UAV設置為在全體UE 的中心(質心)上方懸停,表示為CENTER;第二種使UAV 沿著TSP 算法生成的固定軌跡飛行,表示為TSP,這兩種方案相對簡單且易于實現;將本文所提出的能量最小化方案表示為ENERGY。在不同數據傳輸量Off下的能量消耗如表2所示。 從表2 可以看出,當數據量較小時,能量最小化方案對比TSP 方案具有顯著的優勢,這是因為其飛行距離較短,節省了許多飛行能耗,而由于其飛行軌跡接近于在起飛點附近盤旋,其結果也接近于懸停方案;當數據量逐漸變大,能量最小化方案的能耗逐漸接近于TSP方案,這是由于數據量變大,飛行軌跡逐漸接近于TSP 的軌跡造成的,而在此時使用懸停方案產生的能耗將會顯著變大,這是由于較大的數據量和較低的信道速率導致的較長的懸停時間所導致。而本文所提出的能量最小化方案通過連續凸逼近的方法,平衡了通信速率和飛行距離,在不同的數據傳輸量下都有著更低的能耗。 表2 無人機在不同飛行方案下的能量消耗 單位:JTab.2 UAV energy consumption under different flight strategies unit:J 對于聚類方案的評估,仍然使用圖3 中的UE 分布,在全部UE 的計算卸載的數據量Off固定為10 Mb 的條件下,在不同的機載能量Ecell下聚類的結果和UAV在各個聚類中的飛行軌跡如圖4所示。 圖4 兩種機載能量條件下的聚類結果和飛行軌跡對比Fig.4 Comparison of clustering results and flight trajectories under two airborne energy conditions 在圖4 中,在Ecell為10 kJ 時,分成了3 個聚類;在Ecell為15 kJ 時分成了2 個聚類。由此可以看出,UAV 的機載電池儲存的能量越大,其在一次飛行中可以訪問的UE 數量越多,每個聚類中的樣本數量也就越大。若以每個UE 的數據卸載量Off為變量,在同樣的機載能量Ecell下,得到的聚類結果也遵循此規律,在此不再贅述。 最后,在多種聚類策略中,基于歐氏距離進行劃分的聚類算法適合本文中對UE進行分類的場景,而由于現有的基于劃分的聚類算法需要在算法開始時預先確定k個初始中心點,而在不同的UE 分布場景下,合適的k值也是不同的,因此,為了使算法可以在不同的UE 分布場景中獲得合適的初始中心點數目,設計了一種遞增k的K-Means 聚類算法:從1 開始逐步遞增k,在每次迭代中隨機確定k個聚類中心的位置并使用K-Means算法獲取聚類結果,對所得的k個聚類分別計算UAV訪問此聚類的能量消耗,若有某個聚類的能量超出了Ecell,則k=k+1。直到當k到達某個值時,對于每個聚類,其全部UE的計算卸載數據都可以在一次飛行中收集,算法結束,記當前值k=k*。在此,分別使用K-Means 和K-Means++算法作為上述遞增k的聚類算法獲取聚類結果的方案,將這兩組方案計算出的最終聚類數量與本文所提出的聚類算法計算出的聚類數量進行對比。實驗樣本使用網址http://elib.zib.de/pub/mptestdata/tsp/tsplib/tsp/index.html 中的數據集att48.tsp,為了提高計算效率,取其中的前40條數據并分成4組,并將其中的每條數據的橫縱坐標大小都除以10。在前兩組的對比中,將數據卸載量Off設為25 Mb,機載能量Ecell設為20 kJ;在后兩組的對比中,將數據卸載量Off設為50 Mb,機載能量Ecell設為25 kJ,最終得出的聚類數量如表3所示。 從表3 可以看出,本文提出的算法產生的聚類數量在幾個不同的樣例下都小于或等于K-Means 和K-Means++聚類的聚類數量。這是因為K-Means 算法的結果受初始聚類中心的影響較大,而由于在本文場景下,UE 的分布情況在不同的時間、地點時沒有可循的規律,只能通過隨機生成初始聚類中心的方法來初始化K-Means 算法,當初始聚類中心的位置不夠理想時,最終計算出的聚類數量就會偏大,即使使用K-Means++優化了初始聚類中心點的離散程度,由于某些離群點的存在,其結果仍然不夠理想。而本文提出的方法通過動態分裂與合并來調整聚類的數量,不依賴初始聚類中心的位置,可以廣泛適應不同的UE 分布場景;也不需要逐步遞增聚類數目,可以快速收斂。 表3 在不同數據集上三種聚類算法的最終聚類數量Tab.3 Final number of clusters of three algorithms on different datasets 針對當前UAV 的應用場景及其局限性,本研究以能量約束作為聚類是否可行的標準、以最小化聚類的數量為目的設計了一個自適應的聚類算法。通過解決給定地面終端分布下的能量最小化問題,獲得了一個可以有效判斷聚類方案是否可行的依據,并通過多次分裂和合并,在可以快速收斂的前提下將聚類的數量有效地縮減。該方法可以應用在如智能工業、智慧城市等前沿領域,使用UAV 輔助進行大范圍的信息采集,數據同步。本文將UAV 的起飛和降落點簡單考慮為聚類中心,有一定的局限性。首先,聚類中心所在的位置在現實場景中并不一定支持UAV 起降;其次,UAV 并不一定需要在同一點起降,若考慮起飛和降落點的優化,對于某一聚類內UE 的數據收集所需的能量可能會更小;此外,多次飛行之間并無相互之間的聯系,若在地面設置某些固定的可以為無人機充電的起降點,并將UAV 的起降位置設置為這些起降點,就可將完成各個聚類收集任務的軌跡連接到一起,這意味著全部任務的完成將全程自動,具有更強的實用性。而對于能量最小化模塊,其目標函數將飛行高度設為定值,并未考慮用戶設備的水平高度帶來的影響。因此,下一步的研究將會在能量最小化中加入飛行高度變量,以及優化起降點的選擇,使模型更加符合各種應用場景的需求。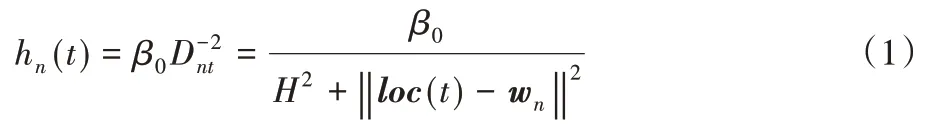
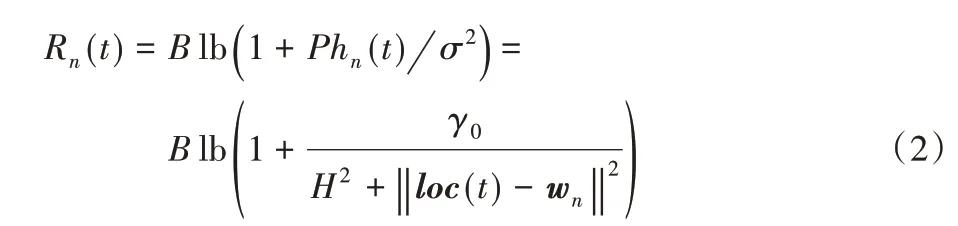

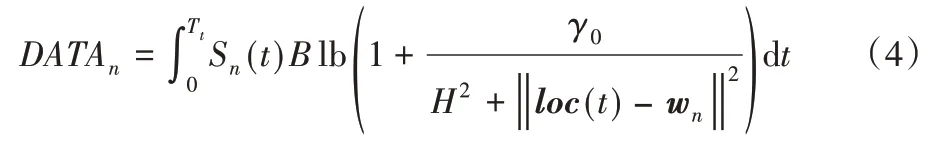

1.2 UAV能耗模型



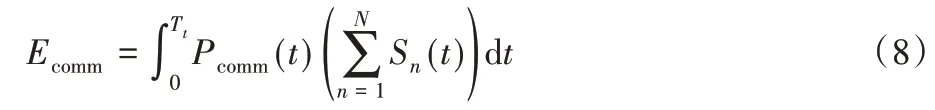


1.3 聚類模型


1.4 問題描述
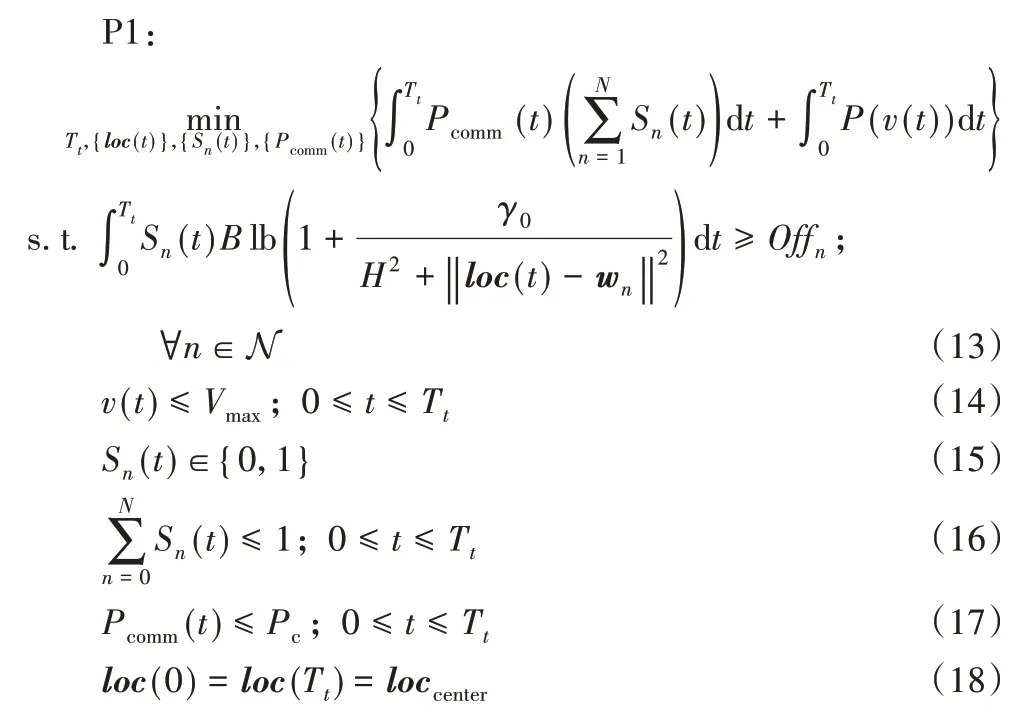
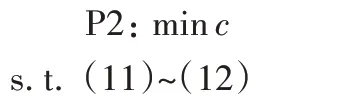
2 能量最小化方法
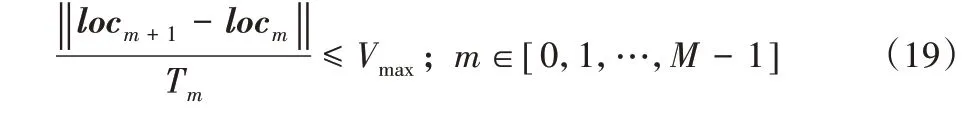

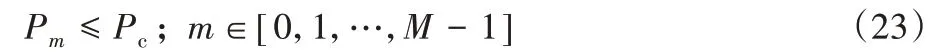

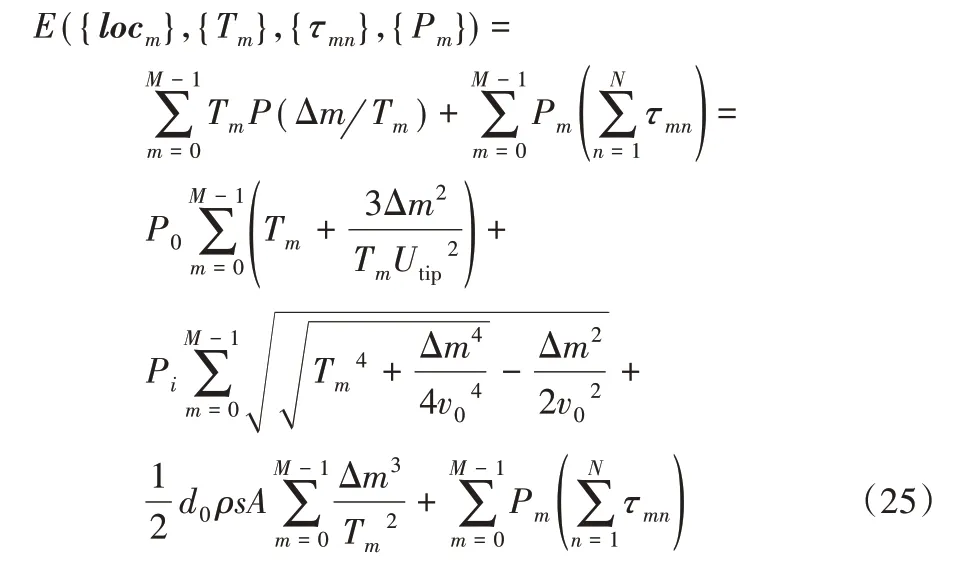
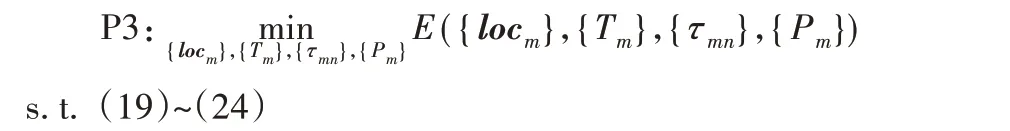

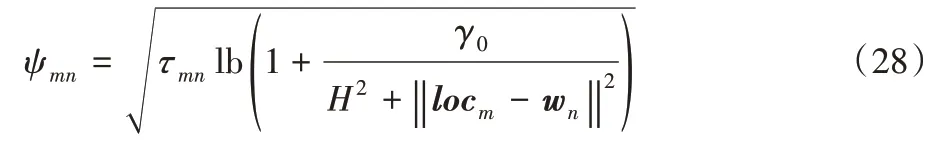

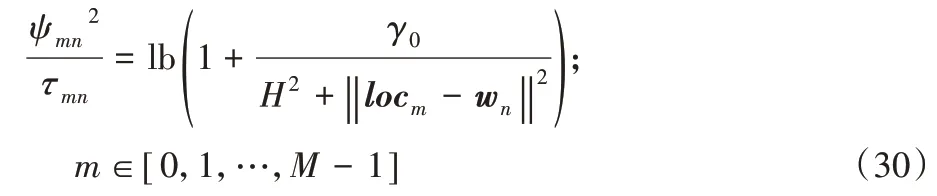
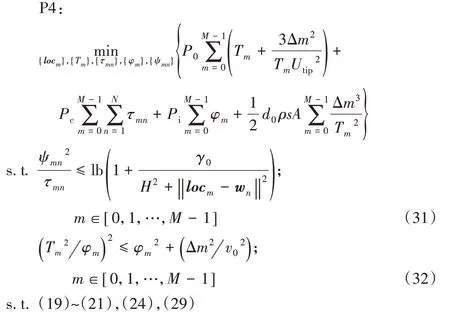



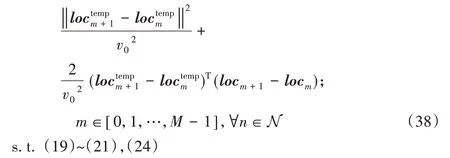


3 自適應聚類方法
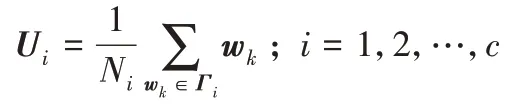


4 仿真實驗與分析
4.1 實驗環境與初始參數
4.2 結果與分析

5 結語

