基于定位不確定性的魯棒3D目標檢測方法

裴儀瑤，郭會明，張丹普，陳文博

（1.中國航天科工集團第二研究院，北京 100039；2.北京航天長峰股份有限公司北京航天長峰科技工業集團有限公司，北京 100039；3.中國科學院自動化研究所，北京 100190）

0 引言

3D 目標檢測是車輛無人駕駛、機器人、增強現實、安保邊防、同時定位與地圖構建（Simultaneous Localization And Mapping，SLAM）等應用領域中的一項關鍵任務。在車輛無人駕駛過程中需要對周邊環境進行實時感知，3D 目標檢測任務可以用于識別并定位車輛周圍的物體，以此躲避障礙物［1-2］；動態環境下的SLAM 是一項充滿挑戰的任務，SLAM 與基于深度神經網絡的3D 目標檢測任務可以互相促進［3］，通過3D 目標檢測任務刪除不可靠的特征點（如移動的物體），提高SLAM 的精度和魯棒性。近年來出現了基于點云投影到圖像［4-6］、基于3D 體素網格［7-9］和基于原始點云［10-12］的3D 目標檢測方法。基于3D體素網格的方法用空間信息進行顯式編碼，將點云數據轉化為體素格式并對體素特征進行編碼；然后，在體素網格上應用3D 卷積進行特征提取；最后，使用候選區域生成網絡（Region Proposal Network，RPN）進行目標預測。稀疏嵌入卷積檢測（Sparsely Embedded CONvolutional Detection，SECOND）網絡［9］是一個具有代表性的基于體素網格的3D目標檢測網絡，其提出的稀疏卷積方法提高了網絡運算效率，加快了網絡推理速度。

目前大部分3D 目標檢測方法的研究都是基于全監督的方法［1，4，7］，而全監督的3D 目標檢測方法需要大量的人工標注數據作為訓練數據來優化模型，由于3D 點云數據的特殊性，在人工標注目標3D邊界框的過程中不可避免地存在偏差，即目標的標注數據中存在噪聲，若使用這種數據作為訓練數據則會對模型的定位精度造成影響；另一方面，在一般的3D 目標檢測方法中，往往輸出結果只有分類置信度以及回歸的3D邊界框［7-9］，而缺少對于3D 邊界框置信度的估計，因此常規的3D 目標檢測器很難區分誤檢（False Positive，FP）和正確檢測結果（True Positive，TP）。誤檢在自動駕駛下非常危險，可能會引起諸如意外制動的情況，降低駕駛的穩定性和效率，因此在考慮目標置信度時除了分類置信度，定位的置信度也是非常重要的，可以用于表征預測3D邊界框的可靠性。本文提出了一種預測3D 邊界框不確定性的方法，在原SECOND 網絡基礎上額外輸出定位不確定性，使用高斯和拉普拉斯兩種方法對定位不確定性進行建模，對定位損失函數進行重新定義并對比了兩種方法的性能。在檢測過程中，聯合使用分類置信度以及定位不確定性對候選目標進行篩選，從而得到更準確的檢測結果，同時也提高了網絡的魯棒性。

1 基于3D體素網格的SECOND網絡

由于SECOND 網絡使用規則的體素網格的形式，能夠顯式地對點云形狀信息進行編碼，同時采用稀疏卷積層可有效提高網絡運算性能［9］，因此，本文選用基于3D 體素網格的單階段3D目標檢測網絡SECOND［9］作為3D目標檢測基礎網絡。

SECOND 網絡結構，如圖1 虛線框內所示，該網絡由體素特征提取器（Voxel-wise Feature Extractor，VFE）、稀疏卷積中間層（sparse convolutional middle layer）和RPN 三部分組成。首先，對點云進行體素化編碼，將點云分割為等大小的體素網格并對體素內的點進行固定數量的隨機采樣。然后，使用VFE 層來提取逐體素特征，VFE 層將同一體素中的所有點作為輸入，使用完全連接網絡（Fully Connected neural Network，FCN）來提取逐點特征。之后通過最大池化層得到局部聚合特征。三維體素特征提取器由多個VFE 層和1 個FCN 層組成，輸出為所有體素的全局特征。隨后，將特征輸入稀疏卷積中間層，通過稀疏卷積解決了三維卷積特征提取造成的內存開銷大以及計算速度慢的問題。該層由兩個階段的稀疏卷積組成，每個階段包含幾個子流形卷積層和1 個稀疏卷積層，在z軸上進行下采樣之后，稀疏的特征圖將轉換為密集特征圖。最后，將中間層得到的密集特征圖輸入RPN 進行候選區域預測，RPN 由3 個階段組成，其中每個階段包括下采樣層和卷積層，再將每個階段的輸出上采樣至相同的大小連接起來，最終應用3個1×1卷積得到3D 檢測結果，包括分類置信度、3D 邊界框回歸值和方向分類預測值。

圖1 整體網絡結構Fig.1 Overall network structure

2 目標檢測中的不確定性

目前已經提出了很多3D目標檢測方法，但對定位不確定性的研究較少。在2D目標檢測任務中，文獻［13］介紹了兩種算法來計算多尺度單發射擊（Single Shot multibox Detector，SSD）［14］檢測網絡的任意不確定性：一種方法是利用異方差回歸法，另一種方法是根據錨框的所有候選框來估計不確定性。實驗結果表明，這兩種方法都會對FP即誤檢結果預測帶來較大的不確定性值。文獻［15］中，在統一實施目標檢測（You Only Look Once v3，YOLOv3）網絡［16］中同樣加入了異方差回歸用于預測邊界框的不確定性，并使用高斯參數構建損失函數，可以提高檢測器有效適應噪聲數據的能力，并對噪聲標注具有魯棒性［17］，實驗結果表明，2D 目標檢測的平均精度均值（mean value of Average Precision，mAP）提升了約3 個百分點，并且顯著降低了誤檢，提高了正確目標的檢測能力。在3D目標檢測任務中，文獻［18］和文獻［19］分別利用高斯參數和拉普拉斯參數構建了3D 目標檢測中邊界框不確定性回歸的模型，證明了邊界框不確定性回歸在3D 目標檢測中的有效性。但這些方法都沒有通過具體的實驗來證明模型提高了對噪聲數據的魯棒性，以及沒有說明定位不確定性在網絡預測后續處理中的具體應用。

3 基于定位不確定性的魯棒3D目標檢測方法

3.1 基于定位不確定性的魯棒3D目標檢測網絡架構

圖1 中，本文網絡使用SECOND 網絡作為主干網絡，并使用1 個除了預測目標分類、3D 邊界框回歸和方向分類回歸結果，另外輸出定位不確定性的新檢測頭。網絡輸出的有向3D邊界框編碼為包含7個維度的向量B=（x，y，z，w，h，l，θ），其中：（x，y，z）代表3D邊界框的中心在三維空間的坐標；（w，h，l）代表3D邊界框的寬度、高度和長度；θ代表3D邊界框以y軸為中心的旋轉角度。本文中的定位不確定性回歸模塊輸出結果為7維向量，即分別對應3D邊界框編碼中每個維度的不確定性。

3.2 定位不確定性損失函數

本文利用額外輸出的定位不確定性，構建新的定位不確定性損失函數，分別使用高斯參數和拉普拉斯參數構造3D目標檢測中的定位不確定性損失函數。

具體來說，對3D邊界框每一個系數的不確定性建立高斯或拉普拉斯模型，即建立了兩種均以3D邊界框回歸結果為均值、定位不確定性為方差的不確定性模型，對應兩種定位不確定性損失函數。

高斯定位不確定性損失函數Lun_reg_Gaussian定義為：

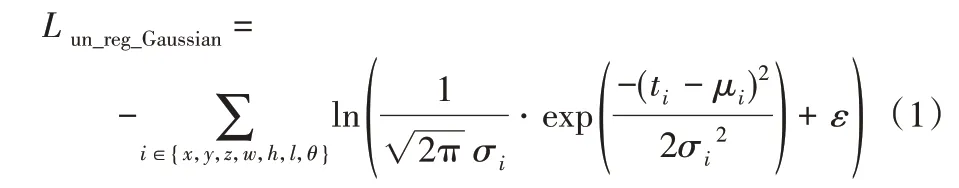
拉普拉斯定位不確定性損失函數Lun_reg_Laplace定義為：

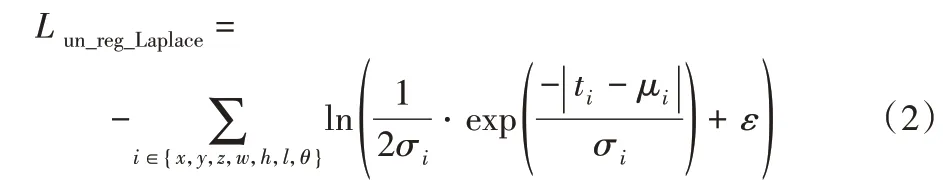
其中，分別對邊界框的每一個維度計算不確定性損失函數，ti、μi和σi（i∈｛x，y，z，w，h，l，θ｝）代表邊界框每個維度的回歸目標值、預測值和不確定性預測值。在計算損失函數之前計算每個維度的回歸目標值如下：

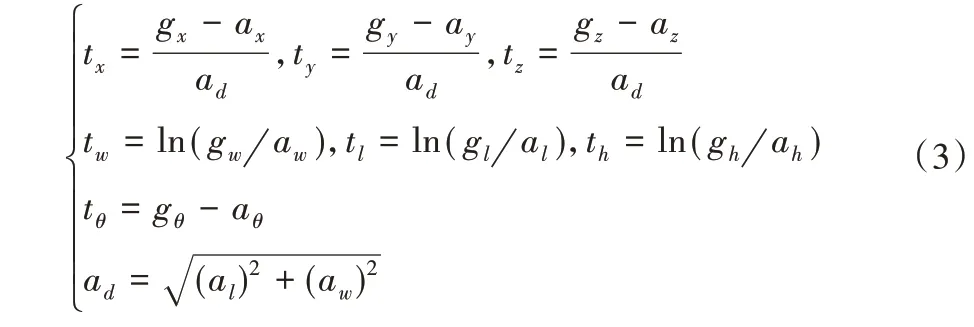
其中：gi和ai(i∈{x，y，z，w，h，l，θ})代表3D 邊界框的真值和定義的錨框。

總損失函數定義為：

其中：為了解決正負樣本不平衡的問題使用Focal損失函數作為分類損失函數Lcls，使用L1 損失函數定義定位損失函數Lreg，Ldir為方向分類損失函數，計算方法同SECOND 原損失函數；β1、β2、β3和β4是超參數，分別為4個損失函數的權重系數。

3.3 基于目標置信度的檢測后處理

在檢測過程中，網絡輸出若干3D候選目標之后會進行一系列后處理操作，篩選得到最終預測目標，包括按目標置信度進行篩選以及采用非極大值抑制（Non-Maximum Suppression，NMS）方法等，在原SECOND 方法中，3D 候選目標的置信度被直接定義為分類置信度，其計算方法為：

其中：outputcls是網絡輸出的分類結果，用于將分類結果轉化到［0，1］區間內，得到的即為分類置信度。本文將分類置信度和定位置信度結合起來，作為目標置信度conftotal進行目標篩選，計算方式如下：

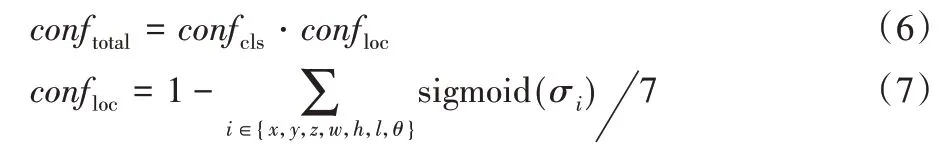
取7個維度的平均不確定性作為每個預測目標的定位不確定性，然后得到定位置信度，將定位置信度和分類置信度結合起來即為目標置信度。在檢測后處理中首先設置置信度閾值，篩除目標置信度較低的候選目標，然后按照置信度進行排序，使用NMS方法篩除邊界框重疊的目標，得到最終的檢測結果。

4 實驗結果與分析

4.1 實驗數據集

在開源的KITTI 自動駕駛數據集［22］中的3D 目標檢測數據集上進行本文網絡的訓練和驗證。該數據集包括了在市區、鄉村和高速公路等多種場景下采集的真實數據，其中，有多種目標類別，例如車、行人、騎車人等。場景中的目標還有各種程度的遮擋和截斷。數據集中共包括7 481幀帶有3D 目標檢測標注的激光雷達點云數據。

本文僅在具有代表性的車輛類別的數據上進行實驗并對比模型性能，對模型在3D 目標檢測和鳥瞰視圖（Bird’s Eye View，BEV）檢測中的性能進行對比評價，使用交并比（Intersection over Union，IoU）閾值為0.7 的3D 平均檢測精度（Average Precision for 3D boxes，AP 3D）和鳥瞰圖平均檢測精度（Average Precision for BEV boxes，AP BEV）作為模型評價指標。對于每一種類別，模型在不同的難度等級上進行驗證，難度等級分為容易、中等和困難，是按照目標遮擋、截斷程度和物體高度劃分的。

4.2 實驗環境

本文實驗使用的操作系統為Ubuntu 16.04 操作系統；計算機硬件配置為Intel Xeon Gold 5220處理器，內存為256 GB，GPU 為NVIDIA GeForce RTX 2080 Ti，顯存11 GB；開發環境為python3.6、pytorch1.1.0，GPU加速庫為CUDA10.0 和CUDNN7.0。

4.3 實驗訓練參數

按照數據集的官方設置，將KITTI 數據分為3 712 幀訓練數據和3 769 幀驗證集。由于檢測的車輛類別目標大小較為固定，本文參照SECOND 網絡，基于KITTI 數據集中車輛類別目標的平均大小，使用固定大小的錨框，即寬×長×高=1.6 m×3.9 m×1.56 m，對每個錨框分配類別、邊界框大小和角度向量作為預測目標。對于車輛類別，若檢測框與錨交并比（IoU）大于0.6，則視為正樣本；小于0.45 視為負樣本；其余樣本在訓練過程中忽略不計。

對于損失函數中各項函數的權重設置，本文實驗中參照SECOND 網絡設置β1=1.0、β2=2.0、β4=0.2，β3設置的對比實驗見第4.4節。本文所有實驗在訓練過程中，都使用one cycle學習率，初始學習率為0.0003，最大學習率為0.003，動量參數為［0.95，0.85］，權重衰減參數為0.01。

本文實驗中的網絡均訓練了60 個epochs（30 000 個迭代），批大小為6，在單個GPU 上的一次完整訓練時長約為7 h，平均檢測速度為每幀2.33 ms。

在實驗過程中，為了增加樣本豐富性，分別在訓練過程中對訓練數據的標注和全局點云數據隨機增加噪聲作為數據增強操作。具體來說，在數據標注中對位置（x，y，z）維度分別進行標準差為（1.0，1.0，0.5），均值為0 的高斯分布中采樣的隨機線性變換，對角度維度加入［-π/4，π/4］區間內隨機采樣的角度。在全局點云數據上，在尺度上進行［0.95，1.05］區間內的隨機變換，以及在角度上加入［-π/4，π/4］區間內隨機采樣的角度。

4.4 不同定位損失函數實驗結果及分析

本文在SECOND 網絡基礎上，在輸出7 維3D 邊界框回歸結果時同時輸出7 維定位不確定性，并在此基礎上實現了兩種定位不確定性損失函數——高斯和拉普拉斯損失函數。為了對比兩種損失函數的效果，分別將其替換或疊加在原網絡中的L1定位損失函數上。

表1 對比了本文方法和其他方法的實驗結果，其中：多視圖3D（Multi-View 3D，MV3D）［4］網絡是基于多視圖的經典網絡，點區域卷積網絡［20］（Point Regions-Convolutional Neutral Network，PointRCNN）是基于原始點云的網絡，VoxelNet［8］、SECOND［9］和結構感知單階段檢測器［21］（Structure Aware Single-Stage Detector，SA-SSD）是基于體素網格的網絡。實驗（A）為本文復現的SECOND 網絡的性能，并將此作為實驗對比的基線模型，實驗（B）和（C）使用不確定性損失函數替換L1定位損失函數，實驗（D）和（E）為不確定性損失函數與原L1損失函數疊加使用。

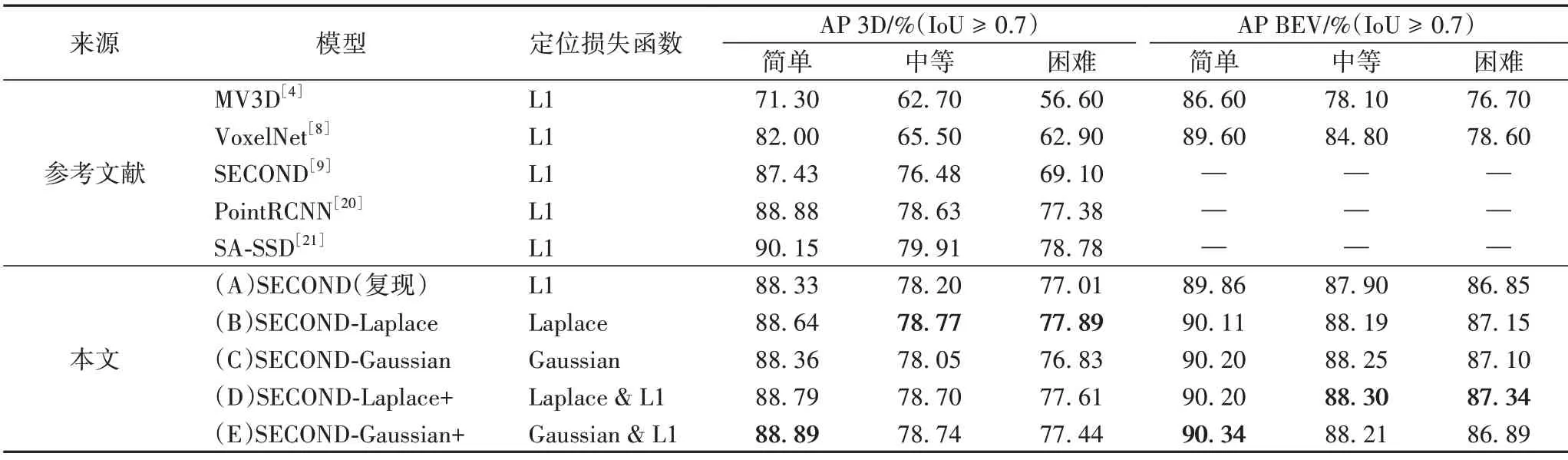
表1 不同定位損失函數對比Tab.1 Comparison of different localization loss functions

對比（A）、（B）、（D），在中等難度上拉普拉斯定位損失函數替換和疊加L1 損失函數分別使平均檢測精度提升0.57 和0.5 個百分點，說明拉普拉斯定位損失函數可以直接替換L1損失函數且保持性能提升。對比（A）、（C）、（E），在中等難度上用高斯損失函數替換L1 損失函數會降低平均檢測精度0.15個百分點，但在L1基礎上加入高斯損失函數可以提升平均檢測精度0.54 個百分點，并可以達到與（B）基本相同的性能。綜合對比實驗結果（B）到（E）證明了不確定性檢測頭的有效性，高斯和拉普拉斯兩種對定位不確定性的回歸方式都可以輔助3D邊界框的回歸，但拉普拉斯定位損失函數帶來的性能提升優于高斯，這是因為拉普拉斯的回歸方式更加接近L1損失函數。

圖2為不同網絡在KITTI驗證集上進行3D 目標檢測的可視化效果，可以看出不確定性檢測頭相較原SECOND 網絡得到的檢測框更準，并且可以篩選部分誤檢結果，說明不確定性可以有效用于3D邊界框的篩選。

圖2 不同模型在KITTI驗證集上的檢測效果Fig.2 Detection effects of different models on KITTI validation set

圖3 為訓練過程中各個模型的準確率變化折線，可以看出雖然原SECOND 網絡在訓練初期準確率上升較快，但后續有較大起伏，而增加了拉普拉斯和高斯定位損失函數的模型在整個訓練階段準確率逐步提升直至穩定，易收斂。

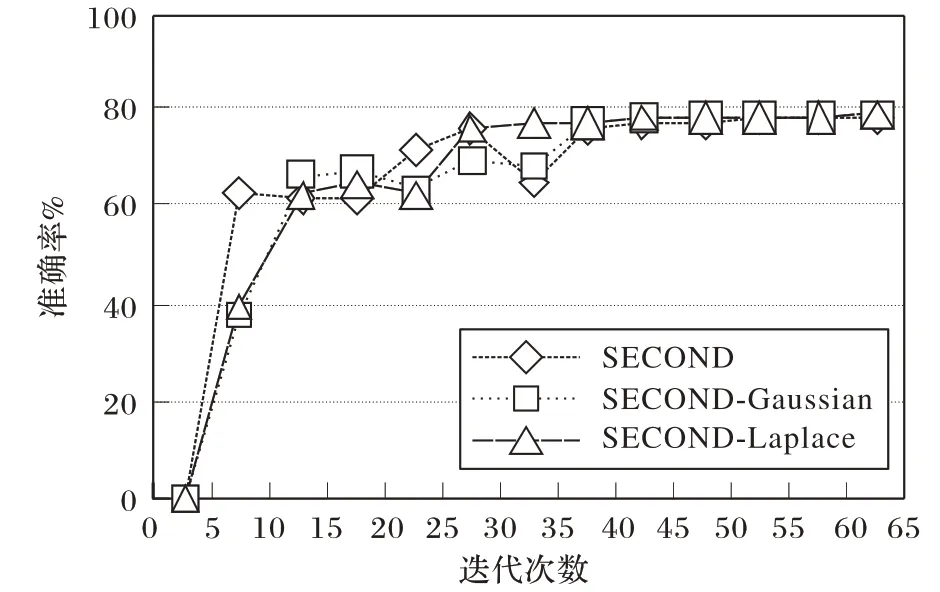
圖3 不同模型在KITTI驗證集上的準確率Fig.3 Accuracies of different models on KITTI validation set

將不確定性損失函數與L1損失函數疊加時，需考慮不同的權重情況，以得到最優的疊加方式，表2 展示了使用不同權重β3對不確定性損失函數加權的結果。對于拉普拉斯損失函數，其權重為0.5 時模型準確率最高；對于高斯損失函數，其權重為0.01時模型準確率最高。

表2 定位不確定性損失函數在不同權重下的對比Tab.2 Comparison of localization uncertainty loss functions with different weights

4.5 魯棒性實驗結果及分析

為了驗證定位不確定性對于噪聲標注數據的魯棒性，本文模擬了人工標注數據的不準確性，在訓練數據標注中隨機加入不同尺度的噪聲擾動。表3 中的實驗表明，本文提出的改進SECOND 模型對于噪聲數據更加魯棒。本文分別在物體的尺寸（長、寬、高）、位置（x、y、z維度上的坐標）以及旋轉角度上加入不同尺度的隨機數作為噪聲擾動，以模擬人工標注數據中可能存在的噪聲數據。例如尺寸（-0.10，0.10）表示在訓練數據的標注中，將尺寸維度長、寬、高3 個數據上分別加入（-0.10，0.10）范圍內的隨機數，作為該物體的真實標注值對模型進行訓練。表3中模型S代表SECOND原始網絡，L代表最優設置的SECOND-Laplace 模型，G 代表最優設置的SECOND-Gaussian+模型。實驗結果表明，尺寸數據中的噪聲對三個模型影響都較小，（-0.20，0.20）范圍內的擾動僅使三個模型在中等難度上準確率下降2.3、1.7、1.7 個百分點，位置噪聲在（-0.20，0.20）范圍內的擾動使三個模型在中等難度上準確率下降高達7.2、4.7、5.3 個百分點。在噪聲數據上兩個改進模型的魯棒性均比原始網絡好，尤其是在噪聲較為嚴重時，改進模型準確率下降程度遠小于原始模型，其中SECOND-Laplace 模型相較SECOND-Gaussian+模型基本對于每一種類型的噪聲數據都更為魯棒。

表3 不同模型用噪聲數據訓練對比Tab.3 Comparison of different models on training data with noisy data

5 結語

本文提出了一種基于定位不確定性的魯棒3D 目標檢測方法，在一定程度上解決了訓練數據中的3D目標檢測框可能存在的人工標注不準確問題。在SECOND 網絡中加入對定位不確定性的預測，利用拉普拉斯和高斯兩種分布模型構造定位不確定性損失函數，并在檢測后處理中結合分類置信度和定位不確定性進行候選框篩選。所提算法在KITTI 數據集中等難度的檢測準確率達到78.77%，相較原始SECOND 網絡提高了0.5 個百分點；在訓練數據有噪聲的情況下，檢測準確率比原始SECOND 網絡最多提高了3 個百分點。本文方法提高了對于帶噪聲訓練數據的魯棒性，減少了誤檢并提高了定位精度，但在KITTI 驗證集上的結果與原方法相比準確度提升不多，仍有提高的空間，可以考慮對定位不確定性的建模方法進行更深入的研究。本文提出的方法具有通用性，理論上可以應用于其他3D目標檢測方法網絡中。