可穿戴式人體姿態識別系統研究進展

宋賀良,鄭 毅,王克強

(華北光電技術研究所,北京 100015)

1 引 言

可穿戴式人體姿態識別系統已在智能家居[1]、虛擬現實[2]、病人實時健康監測[3]、體育競技分析以及人機交互場景中被廣泛應用。

基于可穿戴式的人體姿態識別系統相比于非穿戴式的識別系統(如圖像識別技術、電磁定位跟蹤技術和聲學定位跟蹤技術)有著獨特的優勢(見表1),并且可使用的傳感器類型較多,常用的無線通信方式有WiFi、藍牙和Zigbee,可以比較全面的記錄與人體行為相關的各種數據,已經發展為一種非常實用的現代技術。具體實現為將傳感器通過嵌入式技術,采集人體多種生理信息后通過無線通信技術傳輸到智能終端處理分析數據。

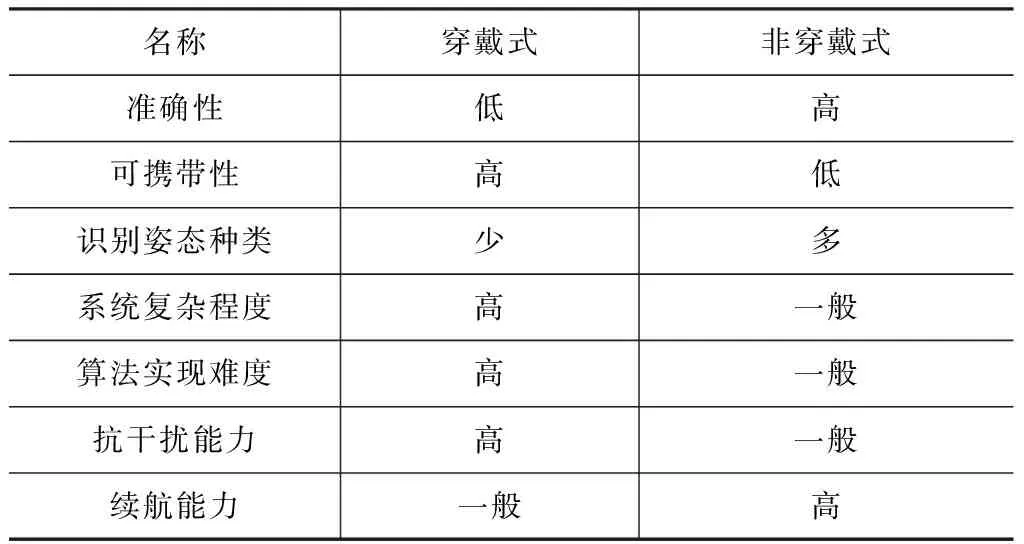
表1 非穿戴式和穿戴式技術對比表Tab.1 Comparison table of non-wearableand wearable technology

2 加速度計進行姿態識別

2.1 單軸加速度計

在可穿戴式人體姿態識別技術初期,研究人員使用單軸加速度計來識別人體行為。Servais等人[4]研究發現將加速度計放置在加速度變化較小的位置(如腰部、背部)識別效果要好于變化較大的位置(四肢)。Carlijn等人[5]將三個單軸壓阻式加速度計(如圖1所示)獨立正交安裝在12 mm×12 mm×12 mm的空間中,佩戴位置選擇在腰椎,通過頻率與幅度識別人體日常活動行為,識別率為30 %～40 %。J.B.J.BUSSMANN等人[6]將四個壓阻式加速度計分別放置在大腿以及胸部,選擇角度、運動信號和頻率三個特征值,預設閾值后識別了20多種不同的姿態,但是特征提取與姿態識別花費了30 min。Kristof等人[7]通過使用兩個單軸加速度計佩戴在褲子上,并通過使用KSOM聚類算法(如圖2所示)分類,站與坐兩種姿態識別率達到95 %,但是上下樓梯識別率僅有50 %,并且算法復雜,只能離線處理數據。

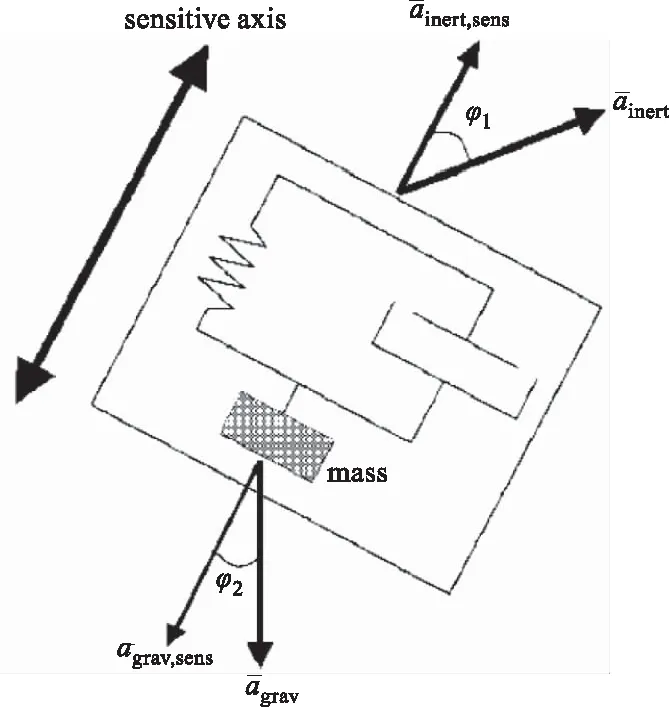
圖1 壓阻式加速度計圖Fig.1 Piezoresistive accelerometer

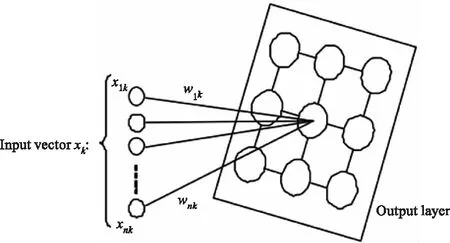
圖2 KSOM算法示意圖Fig.2 Schematic diagram of KSOM algorithm

2.2 三軸加速度計

隨著剛體姿態估計理論與加速度計工藝技術的成熟,研究人員開始采用三軸加速度計來評估日常行為姿態,三軸加速度計用于測量載體的三軸運動加速度,具有體積小和重量輕的特點。

如圖3所示，在導航學中:橫滾角(Roll Axis)φ:機體軸X軸與水平面的投影之間的夾角,區間(-180°～180°)；俯仰角(Pitch Axis)θ:機體軸Y軸與水平面的投影之間的夾角,區間(-90°～90°)；偏航角ψ(Yaw Axis):機體軸Y軸在水平面上的投影與地軸Y軸之間的夾角,區間(0～360°)。

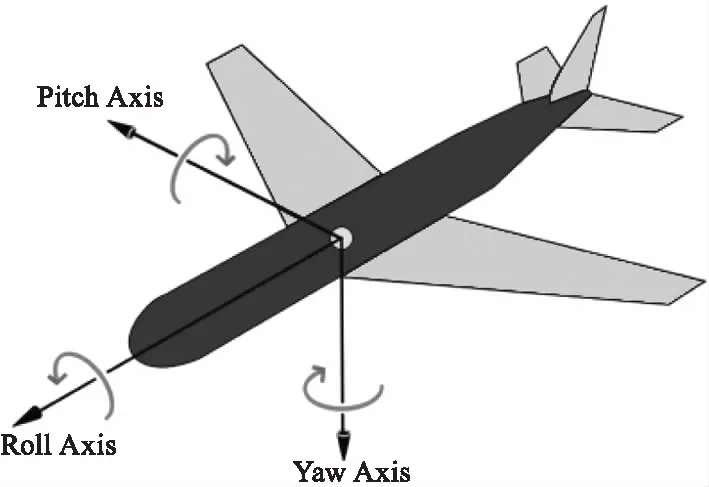
圖3 姿態角Fig.3 Attitude angle

如圖4所示，當三軸加速度計為靜止狀態時加速度計的輸出僅為重力加速度g,因此針對這個靜態輸出的特性,可以對此構建與三個軸輸出的比例關系方程,從而可以解算出姿態角。

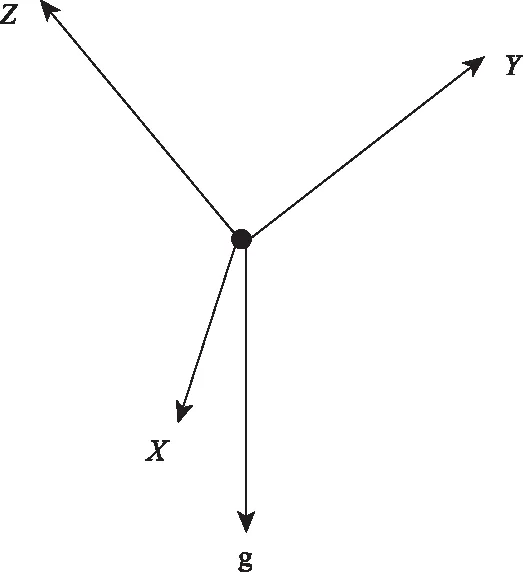
圖4 加速度法求解姿態角Fig.4 Acceleration method to solve attitude angle

其中g為重力加速度方向,X、Y、Z三個軸為加速度計測量軸,根據矢量關系可計算出俯仰角與橫滾角。加速度法求姿態角有著計算步驟簡單和沒有誤差累積的優點。但是此方法無法計算出偏航角,無法得到較為完整的姿態數據,并且在人體運動時所測得的數據為重力加速度和運動加速度的疊加量,即使用濾波器從測得的加速度數據中消去運動加速度分量仍會導致數據延時,很難達到實時精確求解姿態的要求。

Zhenyu He[8]使用離散余弦變換和主成分分析減少特征信息,張潔[9]解決特征降維問題時同樣采取了主成分分析,后利用ReliefF算法重新計算每個特征的權值,再針對計算結果中不同的特征權值而獲得分類的依據,選擇特征權值最大的幾個特征組成特征子集。最終均采用支持向量機進行姿態識別。

弗拉基米爾·瓦普尼克[10]在1995年發表了最初的SVM文章,當時這篇文章被Machine Learning著名期刊要求命名為“支持向量網絡”發表。支持向量機的學習是在特征空間進行的,考慮一個二類分類問題時,支持向量機的基本思想就是在樣本空間中確定一個超平面,可以將需要分類的集D劃分。面對小樣本學習的問題,采用了結構風險最小化原則代替經驗風險最小化原則,得到了廣泛應用。

2.2.1 線性可分支持向量機

假設ωTx+b=0為確定下來的超平面,法向量:ω=(ω1;ω2;…;ωd),位移項為b,分別確定了超平面的方向和超平面到原點的距離,樣本空間中,隨意的點x到這個超平面(ω,b)的距離可表示為:

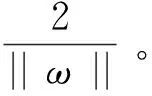
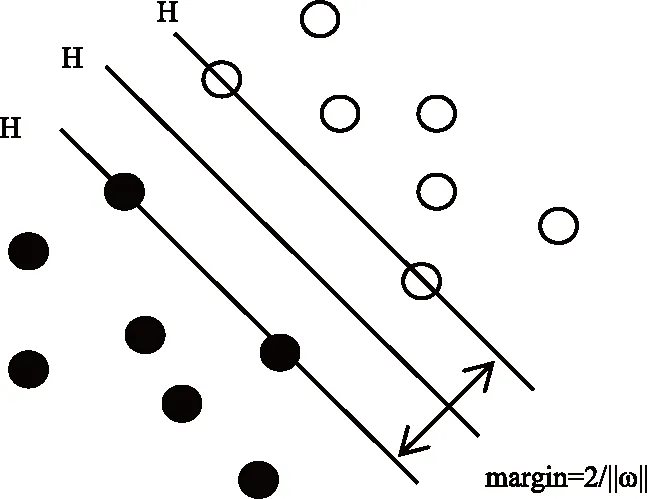
圖5 幾何間隔Fig.5 Geometric interval

依據拉格朗日對偶性的理論,根據求解對偶問題的最優解從而求解出劃分超平面與決策函數。

2.2.2 非線性支持向量機與核函數

如果遇到線性不可分問題,一般情況下是在訓練集中存在某些特異點,將其去除后其余大部分的樣本點集合仍然可以線性可分,要使用軟間隔最大化分類,即引入一個松弛變量,但是在現實問題中往往會出現算法敘述的情況。

如果在現實問題中,原始的樣本空間數據并不能使用線性模型正確劃分,我們可以先通過一個解變換將非線性問題轉變為線性問題,再按上述方法求解轉變后的線性問題,即可解出原始非線性問題。通過使用核技巧首先將原始空間中的數據轉變到一個新空間中,兩空間實例的內積被稱為核函數,再對此新空間應用上述所提到的線性分類支持向量機來訓練模型,很好的簡化了高維模式識別問題。

支持向量機在多分類問題中主要有1-v-r SVMs[11]、1-v-1 SVMs[12]、基于二叉樹的多類SVM[13]三種思路。如果我們所需要區分的種類非常多是,會明顯降低1-v-r SVMs和1-v-1 SVMs兩種算法的分類訓練速度。使用1-v-1 SVMs算法分類時最大的缺點是在區分兩三種比較相似的種類時容易出現無法區分的情況。而在使用基于二叉樹的多類SVM算法時,如果在第一層就存在著誤差,那么誤差會隨著層數累積進而影響算法的分類精度。

徐川龍[14]發現使用SVM分類器高于BP神經網絡的姿態識別率。Putchana等人[15]提出了一種使用無線局域網技術來實時監測老年人運動與跌倒,從三軸加速度計采集信號后通過無線技術發送到計算機；王昌喜[16]使用支持向量機算法識別打乒乓球的三個動作,可以達到98 %的正確識別率。

3 傳感器進行姿態識別

但是與身體運動相關的信號有著復雜且不規則的波動,僅有加速度信號過于單一,傳統的統計方法無法對其分析,隨著微機電系統技術越來越成熟,傳感器有著多種優點:集成效果好、功耗低、造價低和可靠性好等。目前求解姿態角常用的方法有:①將陀螺儀輸出的角速度直接積分求解姿態角；②通過加速度計矢量法求解橫滾角與俯仰角,再根據磁強計求解偏航角；③使用陀螺儀與加速度計融合法求解姿態角；④利用加速度計、陀螺儀和磁強計融合法求解姿態角。

在遇到實際問題時,通常方法①中的陀螺儀具有常值誤差與誤差累積的特性,直接積分會導致解算出的姿態角誤差較大；方法②中前文已經提到在運動情況下運動加速度大于重力加速度,并且磁強計的誤差包括多個方面:磁場變化包含地球磁場和在有鐵磁介質的環境使用,也存在姿態角補償誤差；方法③、④是目前較為常用的方法,但是均需要采用數據融合算法。

在進行人體姿態信息采集時,所使用的MEMS傳感器既有多組件組成的方案,也有使用六軸、九軸的運動處理芯片的集成模塊。常用的六軸傳感器有LSM330DLC與MPU6050,其中MPU6050是由三軸MEMS加速度計與三軸MEMS陀螺儀組成,既避免了加速度計與陀螺儀使用時時間的軸間差問題,也通過集成的方式減少了封裝空間。

3.1 姿態角解算

在描述姿態時有三種常用方法:運用歐拉角法方程較為簡單,并且求解不需要正交化處理,但是每一個方程都含有三角函數,計算繁瑣復雜,在俯仰角為90°時容易出現結果不確定的結論；方向余弦法在90°時不會出現無解的狀況,但是需要求解九個微分方程,計算復雜不適用于可穿戴姿態識別系統實時求解；四元數法中的三軸角速度可以由陀螺儀測出,只要確定某一時刻的初始四元數和角速度,通過求解四個微分方程就可以解出任意時刻載體的姿態四元數和姿態角。因此四元數法的實用性更出色。

當我們在描述人體姿態時,需要定義一個可以描述姿態的坐標系,在選擇參考坐標系時,一般我們選擇地理坐標系,載體坐標系相應的用人體坐標系來確定,由坐標變換矩陣轉換。

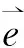
使兩個坐標變換矩陣元素對應相等,可以得到姿態角與四元數的轉換關系,再通過求解四元數的微分方程即可求解人體姿態角。

3.2 人體運動數據預處理

在實驗中進行人體姿態數據采集時,傳感器容易產生外界環境和自身的誤差,這些噪聲會對之后的數據處理產生干擾,在數據預處理時,中值濾波、高斯濾波、卡爾曼濾波和小波閾值去噪是目前平滑去噪較為常用的選擇。張玉蓮等研究人員[17]采用Allan分析法結合Kalman濾波算法,從而對MEMS陀螺隨機誤差建模并加以補償。趙祥欣等人[18]采用中值濾波的技術,從而消除三軸加速度計的脈沖噪聲。李世心等人[19]對陀螺儀去噪時采用平穩小波并得到了很好的結果。卡爾曼濾波算法在信息融合中對陀螺儀去噪有著很好的效果,同時也要建立信號噪聲模型,如果噪聲隨機就并不容易確定噪聲類型,并且算法計算復雜度較高,不太適用于實時傳輸。

3.3 運動數據特征提取

從傳感器中測得的各種數據,都是表征人體姿態的原始信號,與生理相關的信號呈現出復雜且不規則的波動,傳統統計方法無法對其合理分析,需要在原始信號中挖掘出最合適的信息,接下來才可以構建并驗證合適的模式識別算法。傳感器采集信息為某一段時間內的數據,數據點過多導致不適用于直接對信號進行特征提取,常用的辦法是數據分割和時間序列擴充。

特征來源于加速度計數據的窗口,現如今已經使用一系列不同方法從加速度計中提取姿態特征,一些研究人員直接從時域和分析頻域來提取特征,近些年小波分析[20]已被用于推導所謂的時頻特征。小波分析不僅可以確定離散時間序列,還可以導出表征原始信號的時頻特征。需要面對不同的場景時要做不同的處理,應該盡可能選取種類較多的特征進行分析,從而選取出最能夠區分不同姿態的特征。

3.4 人體姿態模式識別

人體運動特征提取后,有不同的算法選擇來區分需要識別的姿態。Qiang Li[21]通過在胸部和大腿兩個部位放置兩個傳感器,計算軀干與重力矢量夾角,再與自己所設定的閾值進行比對,從而確定四種靜態姿勢和跌倒狀態。此系統雖然模式識別正確率比較高,但是采用閾值分析,結果不具有普適性。Yeoh W S[22]選取了三個雙軸加速度傳感器來檢測人體姿態(躺、坐、站立)和步行速度,一個傳感器安裝在腰上,其余兩個安裝在大腿上。分類器首先通過判斷是否為周期性的步態活動來確定人處于靜態還是動態,再根據姿態分類器基于軀干、左大腿與右大腿的彎曲角度來判定基礎活動。此系統通過估算軀干與大腿的彎曲角度后進行閾值分析,理論上識別率會比單傳感器更高,如果將閾值判斷換為機器學習算法判斷,識別率會更高,但是計算兩個傳感器之間夾角過于繁瑣,且需要額外佩戴一個主控芯片,通信及可靠性問題也需要解決,整個算法的工作量較大,不適合實時判斷姿態變化。

Verma的團隊[23]使用Sparkfun 9DOF RazorIMU(九軸)傳感單元,通過多尺度熵分析(MSE)與模糊邏輯算法(FL),有效識別了六種不同的人體姿態及跌倒狀態。李路[24]使用三軸加速度計與三軸陀螺儀的組合,將傳感器單元佩戴在人體腰部,采用四元數求姿態角,并提出了一種基于加速度計校準人體姿態角的方案:當人在靜止狀態下,可以選取一個靜態校準點,通過加速度計求出的橫滾角與俯仰角進行校準；當人在運動狀態下,選取合加速度為1g時,此時加速度處于下降沿時,選其作為動態校準點來校準四元數法求出的姿態角,并采用支持向量機算法進行姿態識別。

4 展 望

現在實驗所選擇的監測節點較多,需要基于人體姿態動力學模型進行建模分析,雖然算法邏輯清晰且精度高,但是測量時傳感器位置偏差會隨時間累計,另外在無線傳輸時需要考慮數據同步,受外界干擾嚴重并且傳輸不穩定,在接下來的研究中可以采用傳感器較少并且無線傳輸通道較少的方案。

在解算人體姿態角時,描述姿態常用的方法是基于四元數的卡爾曼濾波法,在融合各種數據時是將加速度計和磁強計近似看作線性系統來使用卡爾曼濾波方程,接下來的研究可以使用擴展卡爾曼濾波或者無損卡爾曼濾波對數據進行融合。

對運動數據特征提取時,在實驗中[25],快速傅里葉變化頻域特征在單傳感器測量時比時域特征和小波分析具有更高的判別能力,但是特征分析不能一概而論,不同方向和位置的特征對待分類的表現程度不一,在以后研究中可以在特征提取時測試多種方案。

現如今使用最常見的模式識別算法是支持向量機,雖然識別率很高,但是一般需要訓練比較多的支持向量機,計算量大且運算過程繁瑣,如果想將算法移植到終端比較困難,如何在保證識別率的基礎上優化算法是接下來工作的重點。

5 總 結

隨著微機電技術的研究發展,目前所研究的人機交互應用領域也不斷擴大,可穿戴式人體姿態識別技術是一種涉及多學科、多領域的人機交互技術,包括人體運動學、傳感器技術、信號處理等復雜學科的一項系統工程。本文從最開始所僅采用加速度計到現在采用慣性傳感單元的進展進行論述,重點對可穿戴式人體姿態識別技術的實現方法進行梳理總結。最后,結合這項技術還存在的某些不足對未來科研進行了展望,對相關技術的深入研究有所幫助。