基于量綱分析的巖質邊坡穩定性分析模型
王曉琪
(本溪泓源供水有限責任公司,遼寧 本溪 117000)
0 前言
巖質邊坡穩定性與巖石強度參數及自身結構密切相關,同時,受到賦存環境的影響,如水位循環升降以及高寒地區凍融循環等,因此,巖質邊坡穩定性問題一直以來為巖土工程領域研究熱點與難點[1-3]。目前,針對邊坡穩定性評價,建立大量有效的評價方法與定量指標,基于強度折減法的邊坡安全系數是評價邊坡安全狀態的重要參數[4-5]。對于不同影響因素條件下邊坡安全系數,正交分析法能夠充分考慮多種邊坡參數的影響,并能夠減少模型樣本容量[8-9]。量綱分析是研究復雜工程問題重要方法,通過確定問題的基本量,建立基本量與研究指標的數學模型,姚囝等[6]針對緩傾斜空區頂板穩定性問題,建立基于量綱分析的采空區頂板穩定性分析模型;岳哲等[7]提出基于量綱分析的巖石相似材料抗壓強度計算模型;趙國彥等[8]基于量綱分析法建立金礦巷道圍巖松動圈預測模型;趙康等[9]基于量綱分析構建金屬礦山覆巖垮落高度預測模型。巖質邊坡安全系數與巖石強度參數、坡體結構特征等密切相關,因此,利用量綱分析法建立邊坡安全系數分析模型具有重要實踐意義。基于正交試驗分析與量綱分析法分析邊坡穩定性,通過正交試驗方法構建不同邊坡參數組合,利用有限元強度折減法得到邊坡安全系數,同時,基于量綱分析原理建立巖質邊坡穩定性分析模型,能夠為巖質邊坡穩定性評價提供基礎參考。
1 量綱分析法
巖質邊坡安全系數是評價邊坡穩定性的重要指標,不僅與巖石強度參數有關,同時,受到邊坡結構的影響。考慮巖石重度、彈性模量、泊松比、粘聚力、內摩擦角等,建立邊坡數值分析模型研究邊坡安全系數,主要研究方法包括正交試驗法和量綱分析法等。正交試驗法是一種簡便有效的多因素敏感性分析方法,邊坡安全系數分析中考慮重度、彈性模量、泊松比、粘聚力、內摩擦角、坡角以及坡高等7 個因素,每個因素設置5 個水平,不考慮各個因素之間的相互作用。根據正價試驗設計原則建立7 因素5 水平正交表,表示為L25(57),邊坡參數取值范圍及正交水平,見表1。
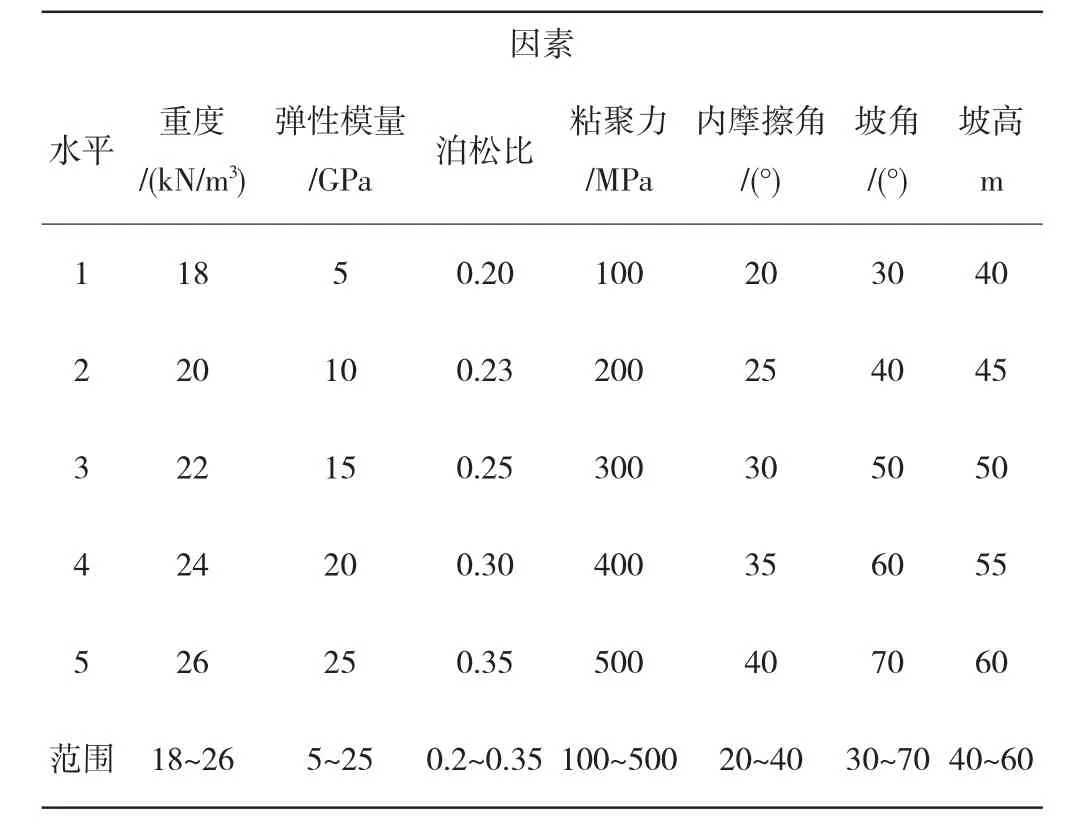
表1 邊坡參數取值范圍及正交水平
通過正交試驗分析結果,采用參數的極差對參數敏感性進行分析,參數的極差越大,說明參數對邊坡穩定性影響程度越大,根據極差分析結果能夠得到參數敏感性結果。
量綱分析是研究尋找參數變化規律,解決工程問題的重要工具。根據邊坡穩定性正交試驗分析結果,通過量綱分析原理得到邊坡安全系數影響的基本量,從而建立安全系數分析模型。量綱分析法的主要內容包括量綱的冪次表示及π 定理,量綱的基本量包括長度、質量和時間,因此,任意導出量均可由不同冪次的基本量表示[10-11]:

π 定理為量綱分析的核心內容,如果問題自變量可以表示為n 個因變量表示,基本量為m 個,因此,可以得到(n-m)個無量綱量,函數關系可由無量綱量確定。
2 邊坡穩定性評價
2.1 正交試驗分析
考慮重度、彈性模量、泊松比、粘聚力、內摩擦角、坡角以及坡高等7 個因素,共設計25 組試驗,利用數值分析方法得到不同試驗組邊坡安全系數(篇幅限制,僅列出8 組),見表2。
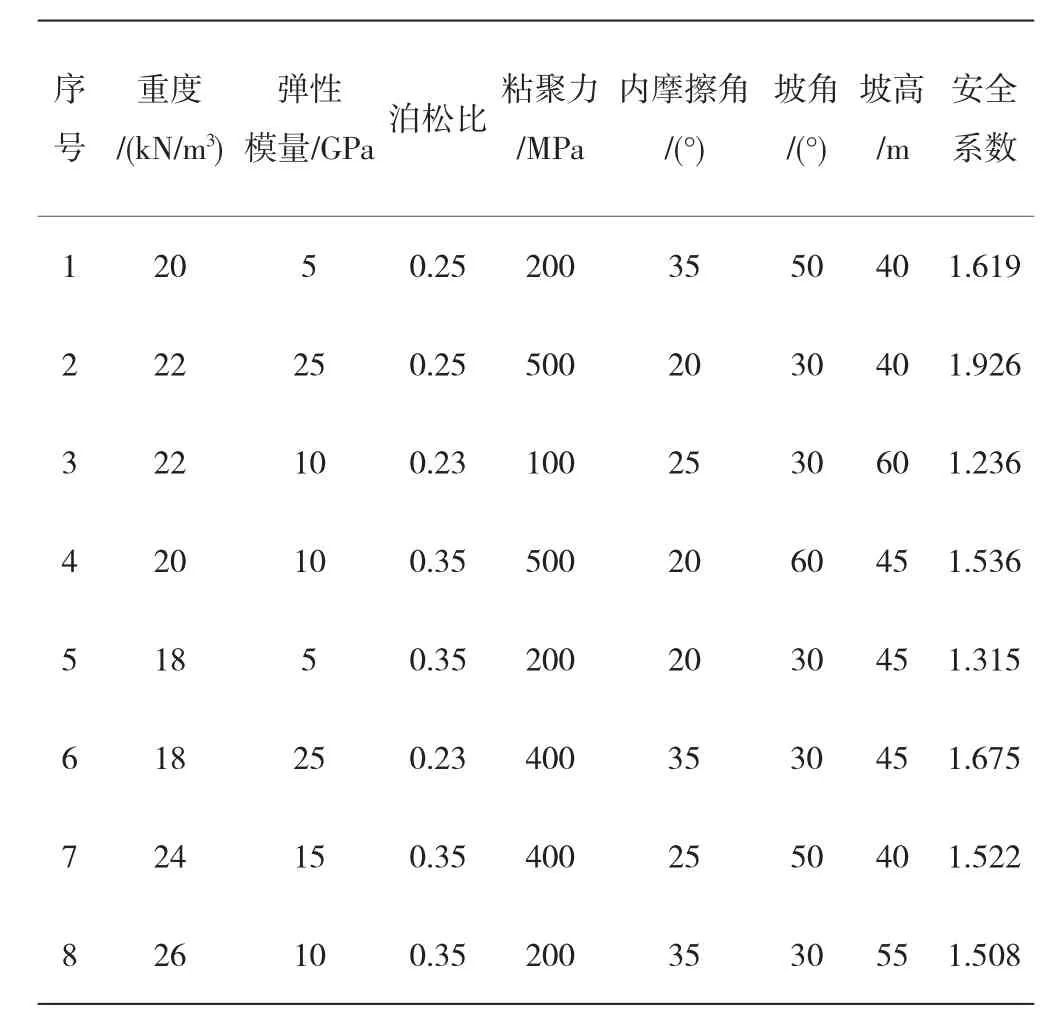
表2 邊坡安全系數正交分析結果
2.2 量綱分析法
根據選取的巖質邊坡穩定性主要影響因素為重度、彈性模量、泊松比、粘聚力、內摩擦角、坡角、坡高等,因此,邊坡安全系數的目標函數為:
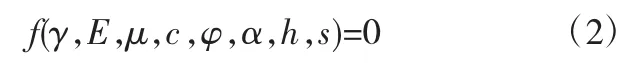
根據量綱分析原理,得到6 個無量綱數,可表示為:
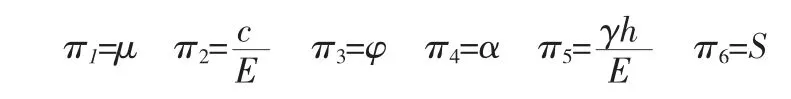
因此,邊坡安全系數的目標函數可表示為:

采用多元冪函數建立目標函數模型,方程形式為:
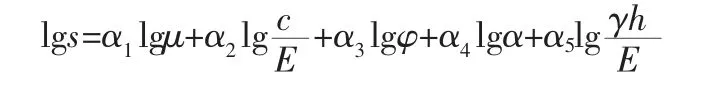
利用MATLAB 對表3 中數據進行回歸擬合,得到表達式中各向系數,模型公式可以表示為:

表3 邊坡無量綱參數對數值
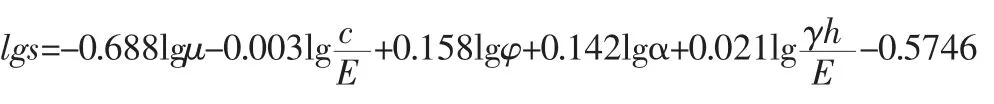
隨機選取正交試驗設計的5 組參數組合作為驗證組,對比分析數值分析結果與本文模型結果,見表4。
根據表4與圖1 可以得到,數值分析結果與本文模型分析結果基本一致,誤差范圍為5.86%~10.51%。結果驗證基于量綱分析原理建立的巖質邊坡安全系數模型的合理性。
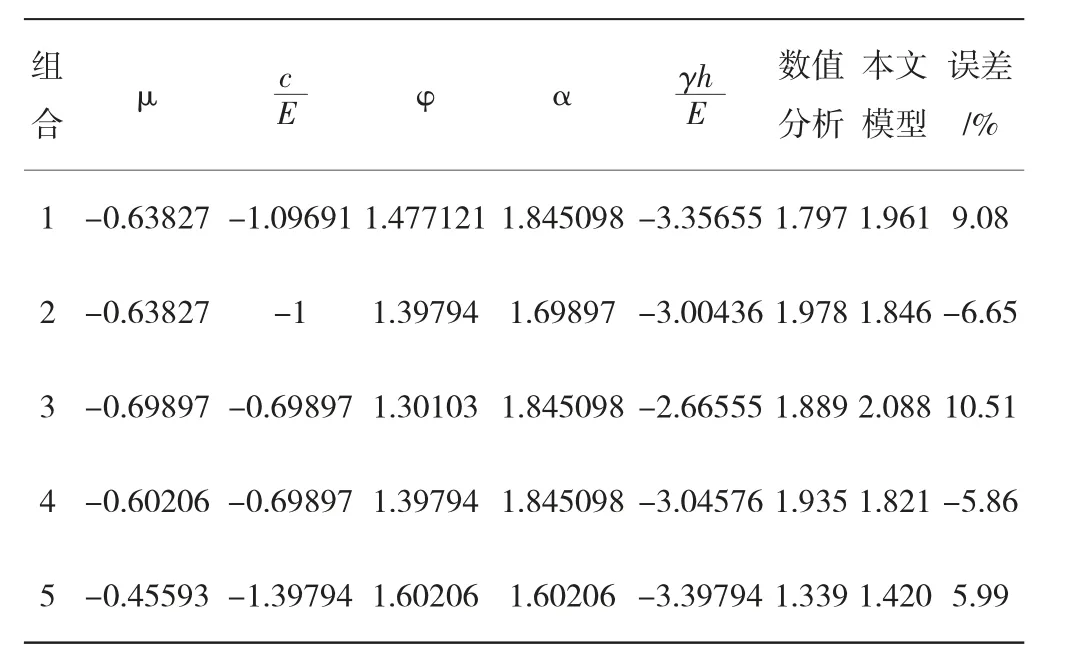
表4 邊坡安全系數結果對比
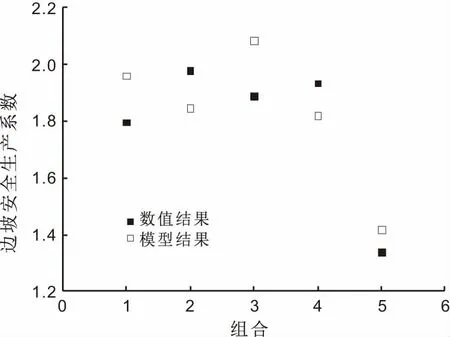
圖1 數值結果與模型結果對比
3 結論
基于正交試驗分析與量綱分析法分析邊坡穩定性,通過正交試驗建立不同參數組合的邊坡安全系數,利用有限元強度折減法得到邊坡安全系數,基于量綱分析原理建立巖質邊坡穩定性分析模型,主要研究結論包括:通過正交試驗方法建立7 因素5 水平的正交表(L25(57)),建立有限元數值分析模型,得到25 組工況下邊坡的安全系數的變化規律。基于主成分分析結果,得到影響邊坡穩定性的主要參數為:重度、粘聚力、內摩擦角、坡角以及坡高;基于量綱分析法,確定影響邊坡穩定性的基本量,并建立巖石力學參數與安全系數之間的數學模型。

