水泥-石灰石粉漿體絮體生長多重分形特征
肖 佳,韓凱東,張澤的
(中南大學 土木工程學院,湖南 長沙 410075)
石灰石粉資源儲量大、分布廣泛,作為水泥混凝土摻和料有環保、節能、利廢的重要意義[1].水泥漿體的絮凝與漿體的流變行為密切相關[2],顆粒間絮凝-解絮的可逆行為在短時間內決定了漿體的觸變性,并導致流變參數隨時間變化[3].學者們通常采用微觀參數表征或顯微鏡觀察水泥漿體的絮凝狀態,Rous?sel[4]通過觸變性模型擬合流變參數得到絮凝結構因子λ和絮凝速率Athix,Ye等[3]利用絮體的平均粒徑研究了水泥基材料靜態屈服應力與絮凝的關系.然而,這些參數都只能反映絮體的平均狀態或尺寸分布,絮體的空間分布也會影響其性能.近年來,研究者采用分形理論來描述絮體顆粒的幾何特征.在絮體生長過程中,絮體的空間和尺寸分布時刻變化,簡單分形維數只能描述絮體生長的平均性和整體性,不能完全揭示絮體分形變化的動力學過程[5].研究表明,水泥漿體的分形維數與測度有關,這也暗示了絮體生長的多 重分形特性[6].Valentini等[7]通過水泥漿體的數字圖像計算其多重分形譜,定量描述了水化硅酸鈣(C?S?H)凝聚.Vahedi等[8]證明了多重分形譜可以提供絮體的內部結構、空間分布、尺寸分布的信息.Gao等[6]也指出多重分形在無需任何先驗假設的條件下可以描述水泥漿體孔隙結構的大小分布和空間排列.本文觀測了水泥-石灰石粉漿體的絮體生長,定量描述了絮體生長的分布特征,并研究了其絮體生長特征與多重分形譜特征參數的關系.
1 試驗
1.1 原材料及配合比
水泥(C)采用P?I 42.5拉法基瑞安基準水泥,比表面積為347 m2/kg;石灰石粉(L)產自湖北荊門,CaCO3含量1)文中涉及的含量、水膠比等除特殊說明外均為質量分數或質量比.為99%,比表面積分別為411、608、807、1 007 m2/kg,依次記為LⅠ、LⅡ、LⅢ、LⅣ;拌和水(W)為自來水.水泥-石灰石粉漿體的水膠比為0.4,其配合比見表1.
水泥-石灰石粉顆粒總比表面積(SSA)計算公式見式(1)[9],計算結果見表1.

表1 水泥-石灰石粉漿體配合比與顆粒總比表面積Table 1 Mix proportions and total specific surface area of cement‐ground limestone pastes

式中:sC、sL分別表示水泥、石灰石粉顆粒的比表面積;φC、φL分別表示水泥、石灰石粉顆粒占固體總顆粒的體積分數.
1.2 試驗方法
按表1配合比制備水泥-石灰石粉漿體:先將漿體慢攪60 s,靜置30 s,接著快攪120 s,再慢攪60 s,靜置90 s,然后慢攪14 min.從水泥水化的第6 min開始,每隔2 min用針狀工具取1個針尖大小的漿體,放在載玻片上,用滴管取1滴無水乙醇滴在漿體上,再放上蓋玻片,放在顯微圖像分析儀下進行觀察,調整光學顯微鏡的粗調和微調焦距,直到所觀察到的漿體圖像清晰,再調整載物臺的位置,找到3個合適位置的圖像留存[3,10].每個試樣采集100像素×100像素的圖像約30幅(見圖1(a));對圖像進行二值化處理,并用黑色表示絮體區域,接著進行邊界濾波和面積濾波,去除面積過小且不影響測試結果的黑色部分(見圖1(b));最后選取合適的絮體圖像進行分割處理(見圖1(c)).

圖1 水泥漿體的絮體圖像Fig.1 Floc image of cement paste
2 結果與討論
2.1 水泥-石灰石粉漿體的絮體生長特征
表2為水泥-石灰石粉漿體絮體面積占比(ξ)與絮體面積平均占比表征絮體生長的平均尺寸分布狀態.由表2可見,隨著水化的進行,漿體的絮體面積占比逐漸增大,絮體的尺寸增大.

表2 水泥-石灰石粉漿體的絮體面積占比與絮體面積平均占比Table 2ξandξˉof cement?ground limestone pastes
為探究石灰石粉對水泥漿體絮體生長空間分布的影響,將絮體圖像用無窮個大小相等的小方格覆蓋(即小方格的邊長要無限小),計算每1個小方格中絮體所占像素.若每1個小方格中絮體的像素值均接近于平均值(標準差越小),絮體分布越均勻,反之,絮體分布越分散.絮體分布標準差σ計算如式(2)所示.
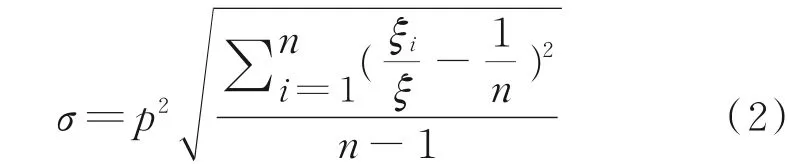
式中:p為絮體圖像像素,取p=100;n為小方格個數,取n=256;ξi為第i個小方格絮體面積占比.
表3為水泥-石灰石粉漿體絮體分布標準差()與絮體分布平均標準差(),表征絮體生長的平均空間分布狀態.由表3可見,隨著水化的進行,水泥-石灰石粉漿體絮體分布標準差逐漸減小,表明其空間分布越來越均勻.
表3 水泥-石灰石粉漿體絮體分布標準差與平均標準差Table 3 and of cement?ground limestone pastes

表3 水泥-石灰石粉漿體絮體分布標準差與平均標準差Table 3 and of cement?ground limestone pastes
Sample C0 CLⅠ20 CLⅠ30 CLⅡ20 CLⅡ30 CLⅢ20 CLⅢ30 CLⅣ20 CLⅣ30 σ 6 min 24.66 18.84 25.37 31.79 34.95 25.37 13.78 17.13 15.25 8 min 15.46 14.13 23.23 15.55 16.30 22.21 20.19 19.43 13.52 10 min 13.76 14.42 16.68 20.57 22.31 15.13 12.64 11.98 11.98 12 min 13.54 12.37 15.12 15.12 21.24 17.06 11.15 12.60 9.45 14 min 13.80 14.07 13.65 14.71 14.49 13.08 13.89 13.37 9.43 16 min 12.17 13.44 14.35 13.17 14.26 12.09 9.29 13.36 9.54 18 min 11.74 10.18 11.07 12.90 16.62 11.41 12.49 11.41 11.04 20 min 10.21 9.21 11.34 11.75 13.54 11.04 7.78 7.54 7.27 σˉ 14.42 14.33 16.35 16.94 19.21 15.92 12.65 13.35 10.93
由表1~3可見:隨著顆粒總比表面積的增加,絮體面積平均占比先減小后增加,分布平均標準差先增加后減小.由此可見,當顆粒總比表面積SSA增加時,絮體生長尺寸減小,分布變分散,而隨著SSA的繼續增加,絮體將有更好的尺寸和空間分布.
2.2 水泥-石灰石粉漿體絮體生長的多重分形特征
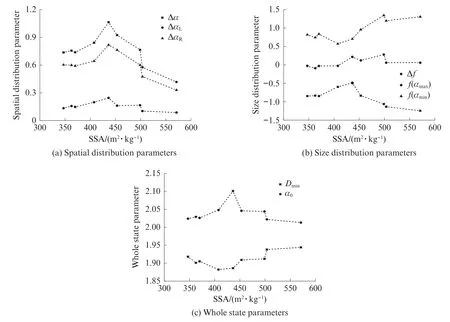
多重分形包括2種關系[11]:(1)各盒子(用i編號)內物理量的概率Pi(ε)與測度ε之間為冪函數關系Pi(ε)~εα,α為奇異性指數;(2)盒子數N(ε)與測度ε之間為冪函數關系N(ε)~ε-f(α),f(α)為多重分形譜函數.假設絮體圖像邊長為1,將圖像用尺寸為ε×ε(ε=1/2、1/4、1/8、1/16、1/32、1/64)的網格覆蓋.q為權重因子,表示各概率子集在配分函數中的貢獻,理論上,q(-∞ 若對于不同的q值,lnIq(ε)與lnε都有良好的線性相關性,說明絮體具有標度不變性,在此基礎上,若τ(q)?q曲線呈上凸形,說明絮體具有多重分形特征.水泥漿體的多重分形特征見圖2.由圖2可見:lnIq(ε)與lnε呈線性關系,尤其對于階次較高的部分(q>0),表現出非常嚴格的線性特征,結合τ(q)?q曲線呈上凸形,證明了水泥漿體絮體生長具備多重分形特征. 圖2 水泥漿體的多重分形特征Fig.2 Multifractal characteristics of cement paste 多重分形理論包括3個重要的組成部分:廣義分形維數Dq、奇異性指數α以及多重分形譜函數f(α),計算公式見式(6)~(8). 水泥-石灰石粉漿體絮體生長的多重分形特征見圖3.由圖3可見:水泥-石灰石粉漿體絮體生長的廣義分形維數Dq為反“S”遞減函數曲線,Dq隨著q增大而減小,曲線在q=0處出現向另一方向彎折的趨勢;當q<0時,Dq隨顆粒總比表面積的增加先增后減,而在q>0時會出現相反的結果;絮體生長的多重分形譜均為左鉤狀,且隨著顆粒總比表面積的增加,多重分形譜先向右發展,然后向左發展. 圖3 水泥-石灰石粉體漿體絮體生長的多重分形特征Fig.3 Multifractal characteristics of flocs growth in cement?ground limestone pastes 多重分形譜中:譜寬Δα可描述絮體的局部特征,代表著絮體的空間分布情況,Δα越大,絮體分布越不均勻;左譜寬ΔαL反映了絮體中大空隙的數目;右譜寬ΔαR反映了絮體中小空隙的數目;譜差Δf反映多重分形譜的不對稱性,代表著絮體的尺寸分布情況,Δf<0時,多重分形譜曲線呈現左鉤狀,反之多重分形譜曲線呈現右鉤狀;右譜值f(αmax)反映小概率對象即大粒徑絮體的數量(αmax為奇異性指數的最大值);左譜值f(αmin)反映大概率對象即小粒徑絮體的數量(αmin為奇異性指數的最小值).將Δα、ΔαL、ΔαR稱為絮體的空間分布參數,Δf、f(αmax)、f(αmin)稱為絮體的尺寸分布參數.最小分形維數Dmin與使f(α)達到最大的奇異性指數α0一起反映了最或然子集的性質,即反映了絮體的整體幾何特征,稱為絮體的整體狀態參數. 圖4為水泥-石灰石粉顆粒總比表面積對絮體生長的空間分布、尺寸分布和整體狀態參數的影響.由圖4可見:當顆粒總比表面積SSA增加時,Δα、ΔαL、ΔαR增加,表明絮體間的小空隙與大空隙數目增加,絮體分布變得分散,但隨著SSA的繼續增加,絮體生長的空間分布出現相反的結果;f(αmin)先減小后增大,即小粒徑的絮體數目先減小后增大,f(αmax)大致保持不變,即大粒徑的絮體數目基本穩定,Δf先增大后減小,即絮體的尺寸先減小后增大;Dmin先減小后增大,α0先增大后減小,延緩絮體生長,而隨著SSA的繼續增加將促進絮體生長. 結合表2、3與圖4可知,絮體面積平均占比與f(αmin)正相關,與Δf負相關,即絮體生長的尺寸平均分布狀態可以用f(αmin)與-Δf來描述;絮體分布平均標準差與Δα、ΔαL、ΔαR正相關,即絮體生長的平均空間分布狀態可以用-Δα、-ΔαL、-ΔαR來表征.由于絮體面積平均占比和絮體分布平均標準差可以描述絮體生長特征,稱之為絮體生長特征參數;絮體生長的空間分布參數、尺寸分布參數和整體狀態參數可以表征絮體生長的多重分形特征稱之為多重分形譜參數.將絮體生長特征參數及多重分形譜參數進行歸一化處理(處理后的數據以下標n表示),其計算公式為: 圖4 水泥-石灰石粉顆粒總比表面積對絮體生長的空間分布、尺寸分布和整體狀態參數的影響Fig.4 Effect of total specific surface area of cement?ground limestone on spatial distribution,size distribution and whole state parameters 式中:xi、xin為第i個歸一化前、后的數據;xmin、xmax為原始的最小值和最大值. 表4為歸一化的絮體生長特征參數及多重分形譜參數,采用BP神經網絡對表4數據進行訓練,以絮體生長特征參數為輸入,多重分形譜參數為輸出,建立水泥-石灰石粉漿體絮體生長特征參數及多重分形譜特征參數的關系.通過計算歸一化后的絮體生長特征參數及多重分形譜特征參數的標準差σ′,對其進行關聯度分析,得到絮體生長尺寸分布與f(αmin)n、-Δfn的關系見圖5,絮體生長空間分布-與-ΔαLn、-ΔαRn、-Δαn的關系見圖6.由圖5可見,-Δfn的標準差小于f(αmin)n,Δfn可以更好地描述絮體生長的尺寸分布,且與絮體生長的尺寸分布負相關.由圖6可見,-Δαn的標準差最小,-ΔαLn居中,-ΔαRn最大,Δαn可以更好地描述絮體生長的空間分布,且與絮體生長空間分布負相關. 圖5 絮體生長尺寸分布與f(αmin)n、-Δfn的關系Fig.5 Relationship between size distribution of floc growth and f(αmin)n and(-Δfn) 圖6 絮體生長空間分布-與-ΔαLn、-ΔαRn、-Δαn的關系Fig.6 Relationship between spatial distribution of floc growth- and-ΔαLn、-ΔαRn、-Δαn 表4 歸一化后的絮體生長特征參數及多重分形譜參數Table 4 Characteristic parameters of floc growth and multifractal spectrun after normalization 綜上,多重分形理論能有效、準確地表征水泥-石灰石粉漿體絮體生長特征,清晰地分析絮體的分布情況,Δα、ΔαL、ΔαR可以用來表征絮體生長的空間分布,且譜寬Δα的準確性更高,f(αmin)與Δf可用于描述絮體生長的尺寸分布,且譜差Δf的準確性更高. (1)當顆粒總比表面積增加時,水泥-石灰石粉漿體的絮體面積平均占比先減小后增加,絮體分布平均標準差先增加后減小. (2)當顆粒總比表面積(SSA)增加時,絮體間的小空隙與大空隙數目均增加,絮體分布變得分散,小粒徑的絮體數目減小,大粒徑的絮體數目基本穩定,絮體的尺寸減小,整體上延緩了絮體生長,而隨著SSA的繼續增加,絮體生長將呈現相反的結果. (3)水泥-石灰石粉漿體的絮體生長具備多重分形特征.多重分形譜的譜寬、左譜寬和右譜寬可以用來表征絮體生長的空間分布,且譜寬更為準確,與絮體生長的空間分布負相關.譜差與左譜值可用于描述絮體生長的尺寸分布,且譜差更為準確,與絮體生長的尺寸分布負相關.

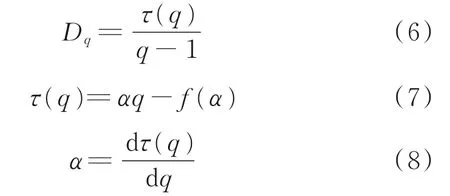

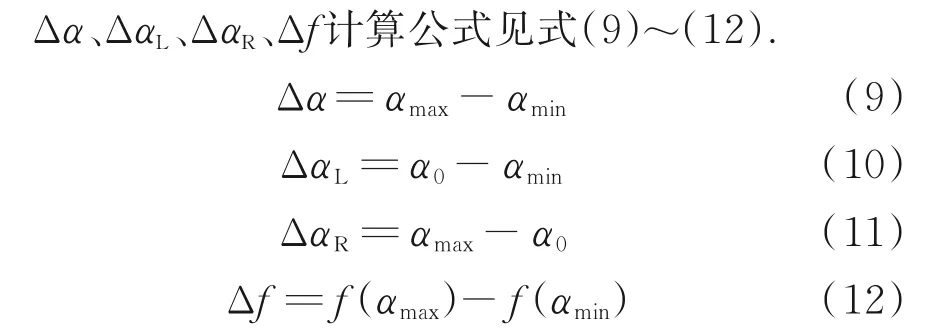
2.3 水泥-石灰石粉漿體的絮體生長特征的多重分形表征




3 結論

