快速仿射非局部均值圖像去噪

陳玲玲，周旭東，謝傢成，劉 乾

快速仿射非局部均值圖像去噪

陳玲玲，周旭東，謝傢成，劉 乾

(揚州大學信息工程學院，江蘇 揚州 225127)

針對仿射非局部均值(ANLM)算法對圖像去噪過程中出現用時過長的問題，提出了一種快速仿射非局部均值去噪(F-ANLM)算法。通過對算法的研究和用時分析得知，仿射變換和關于仿射不變相似性度量的計算這2個模塊占時最多，因此從這2個部分入手提出優化策略。算法首先使用仿射協變結構張量其特征向量的夾角代替尺寸不變特征變換(SIFT)算子的主方向，簡化了仿射變換過程；然后將ANLM方法中的仿射不變相似性度量改寫為離散卷積的形式，使用快速傅里葉變換減少卷積的運算量，加速仿射協變特征區域之間相似性度量的計算。實驗證明，F-ANLM方法簡化了仿射變換和仿射不變相似性度量的計算，與原來ANLM算法相比，速度得到很大的提升。

非局部；結構張量；仿射不變；卷積；相似性度量；快速傅里葉

為了抑制圖像中的噪聲，BUADES等[1]提出了非局部均值(non-local means，NLM)算法，利用圖像的非局部自相似性，收集最相似的圖像塊進行加權平均得到當前像素值，去噪效果得到了很大地提升。但隨著圖像中噪聲水平等級的提高，NLM算法在去噪效果以及保留圖像輪廓紋理等高頻細節信息上，出現了過度平滑的現象。為了提高其去噪性能，ZHAN等[2]用一種非局部SUSAN邊緣檢測算子來自適應地調整圖像像素的平滑系數。此外，圖像塊的大小也影響去噪效果，文獻[3-4]提出利用局部噪聲方差和圖像局部結構來對圖像塊尺寸進行分類。DELEDALLE等[5]提出形狀自適應塊的非局部方法(non-local methods with shape-adaptive patches，NLM-SAP)，即使用不同形狀塊來增加相似塊的個數，緩解“塊效應”。TIAN等[6]提出基于核函數選擇的NLM去噪方法，用新的核函數代替指數函數。文獻[7]通過改進的混合魯棒權重函數來計算圖像塊的相似性權重。FEDOROV和BALLESTER[8]利用仿射非局部均值去噪(affine non-local means denoising，ANLM)算法將仿射變換應用于NLM方法，去噪效果得到顯著提升。

由于NLM在相似度計算中存在大量重復運算，文獻[9]使用平方和圖像和快速傅里葉加快相似度計算，文獻[10]在此基礎上結合Laplacian金字塔再次提高算法效率。本文從減少算法運行時間出發對ANLM算法進行改進：首先利用結構張量簡化仿射變換中旋轉角度的計算，再將仿射不變相似性度量改寫成離散卷積形式，用快速傅里葉變換加速相似度的計算。實驗結果表明，本文提出的快速仿射非局部均值去噪(fast affine non-local means denoising，F-ANLM)算法能夠大大減少ANLM算法的運行時間。

1 仿射非局部均值

ANLM算法考慮利用結構張量生成穩定且獨立的仿射協變區域，以形成橢圓圖像塊，在圖像塊之間加入仿射變換增加相似塊的個數，提高圖像去噪質量。并提出，若直接用圖像的梯度對結構張量進行估計，可能會造成結果的不穩定；若張量具有仿射協變性，那么對于任意一個仿射變換，則有

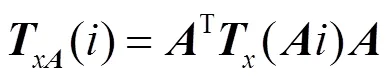
其中，()為關于圖像結構張量的自相關矩陣；為仿射變換矩陣。對于張量()，可以將其與一個以為中心，半徑為的橢圓區域聯系，即

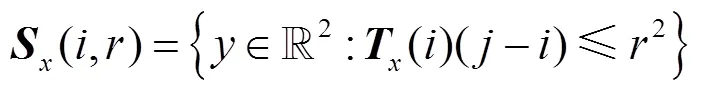
當張量具有仿射協變性(,)=-1(,)，這意味張量可用來構造經過適當仿射變換的仿射協變區域，這些區域是大小自適應的橢圓塊。根據文獻[11]對仿射協變結構張量的迭代過程的陳述，可將結構張量重新定義為

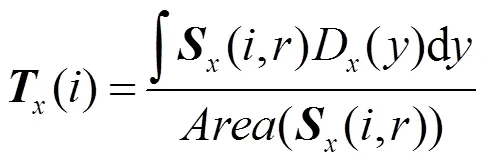
將高斯噪聲看作是隨機方向上的附加梯度，數量為，即噪聲圖像的結構張量為

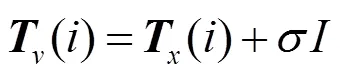
橢圓圖像塊可以通過對噪聲圖像的結構張量進行奇異值分解得到，其大小與有關。結合式(2)和(3)可知：仿射變換后，圖像上的點可以表示為：?()=()，其中，為仿射變換矩陣。

要完全確定，需要找到旋轉角度。ANLM首先將仿射協變橢圓塊歸一化為圓，然后對圓進行仿射變換即旋轉。在變換過程中，選擇使用尺度不變特征變換(scale-invariant feature transform，SIFT)特征點描述子計算旋轉的角度，將梯度方向直方圖中的主能量作為圖像塊的主方向。旋轉圓形區域需與主梯度方向對齊，實現圓形區域的旋轉不變性。

仿射變換增加了相似塊的個數，將中心塊和仿射協變區域中像素點逐一進行相似度比較，最后加權平均得到當前像素點的估計值。

2 快速仿射非局部均值

通過對ANLM方法用時分析可知：計算量主要集中在SIFT旋轉配準和計算放射不變相似性度量上。ANLM算法流程如圖1所示。

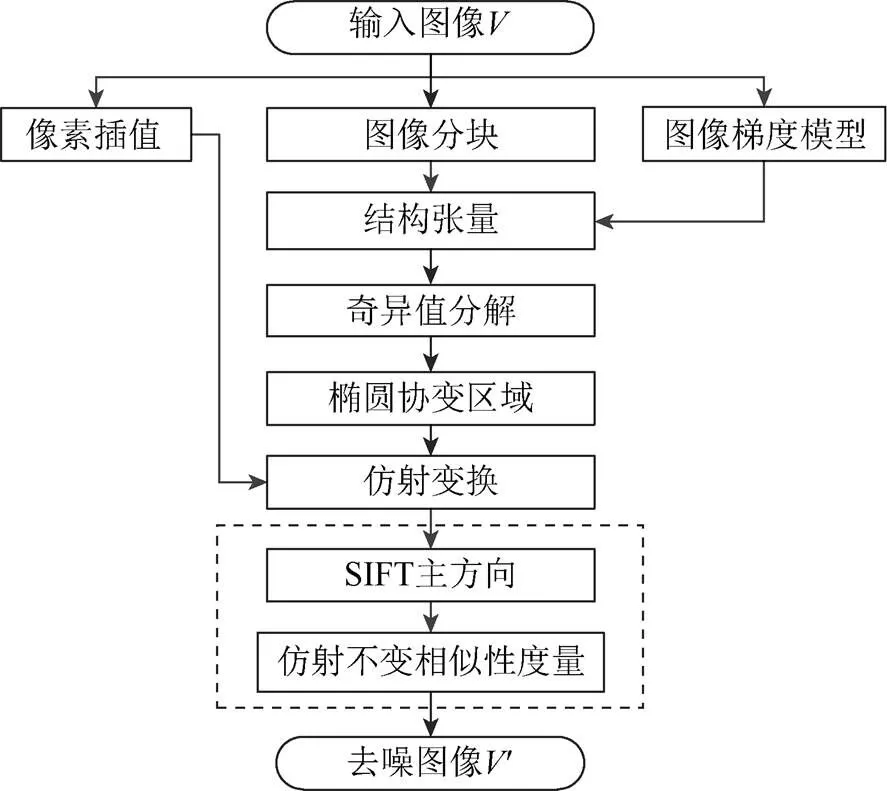
圖1 ANLM算法流程圖

以像素點和為中心的2個相似塊圖像之間的距離可表示為

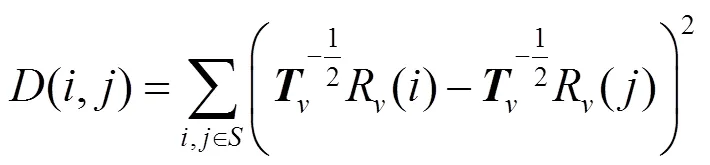
其中，為圓形圖像塊區域，使用指數函數將距離轉換為相似性，則2個圖像塊之間的權重函數為

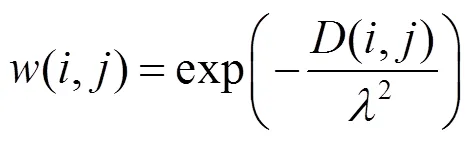
為了對像素點處的圖像塊進行去噪處理，使用其相似性值()作為權重，平均像素點處圓形塊內部的所有像素點，并旋轉圖像塊進行匹配，用加權平均值給出去噪后的圖像塊，即

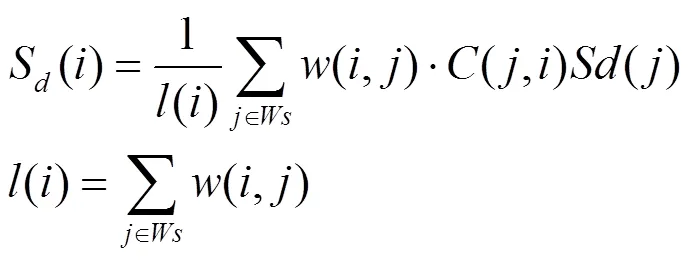
假設圖像的大小為×，以像素點為中心的搜索窗口邊長為，其大小則為×，圓形圖像塊的半徑為，則其外接矩陣的大小為2×2()，還需對圓形圖像塊應用仿射變換，即計算一個圖像塊與其相似塊之間加權歐氏距離需要22，則整幅圖像時間復雜度為(222)。研究發現，在圖1虛線框部分(計算圖像塊旋轉方向和相似性的過程中)存在大量的復雜計算，為了提高ANLM算法效率，構造了F-ANLM算法。主要分2步：①簡化仿射變換；②加速仿射不變相似度的計算。

2.1 計算旋轉角度

ANLM將仿射變換關系化成圓形鄰域的旋轉，選擇使用SIFT特征點描述子，將梯度方向直方圖的主能量作為圖像塊的主方向，旋轉圓形塊需與主梯度方向對齊。但研究發現，這種關于梯度方向的估計方法會使角度存在±20°的誤差，而且算法復雜度高，計算量較大。為了提高運算速度，本文采用仿射協變區域計算給定位置的結構張量求取主方向[12]。

結構張量是一個關于圖像的二階矩陣，ANLM中利用張量形成仿射協變區域，為保證局部鄰域的旋轉不變性，本文提出利用圓形鄰域求取像素點的結構張量，即

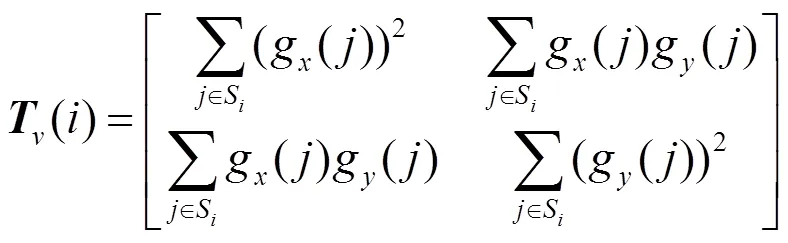
文獻[12]指出，特征向量可以表示特征值所在的方向，該方向與圖像局部鄰域方向一致。因此對上式的結構張量進行特征分解：得到2個特征值及所對應的特征向量，像素點鄰域內的主方向可以表示為

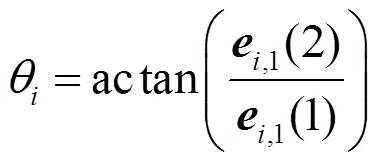
其中，,1為結構張量的最大特征值所對應的特征向量。因此，圓形塊的旋轉角度求解可以直接簡化成求取結構張量的特征向量夾角。

2.2 FFT仿射不變相似性度量

積分圖像作為加速計算相似度經典算法，只適用于方形鄰域。仿射非局部均值最終是求2個圓形圖像塊之間的相似度，積分圖像并不適用，即考慮將歐氏距離重寫成離散卷積的形式

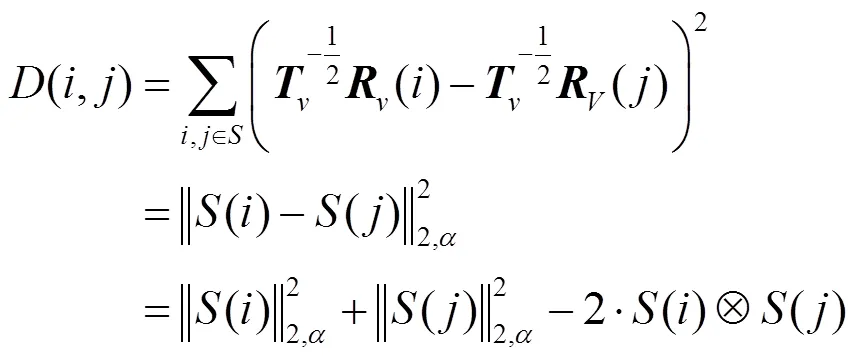
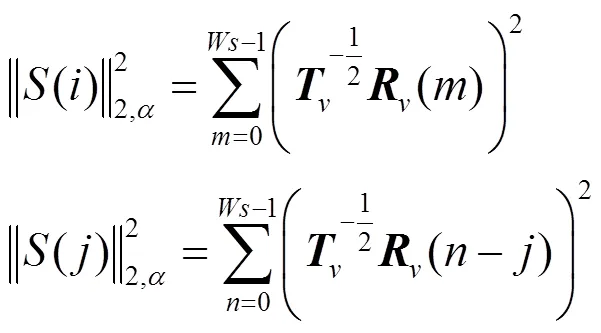
卷積可以借助快速傅里葉變換(fast Fourier transform，FFT)進行加速處理，且計算與圖像塊的形狀大小無關。與積分圖像的思想一致，傅里葉變換是將復雜函數表示成三角函數或是其積分的線性組合。快速傅里葉變換是對離散傅里葉(discrete Fourier transform，DFT)的加速算法，其是基于逐步加倍的思想，在頻域中讓積分求和變為乘法，減少卷積運算的時間。DFT可表示為

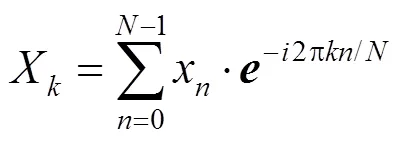
快速傅里葉可看成是DFT和IDFT (inverse discrete Fourier transform) 2部分組成，采用分治思想使多項式能夠快速地進行點值和系數之間的轉換。在圖像中，計算多項式的乘法，可用矩陣相乘的形式替代。卷積使用由表示的2D離散傅里葉變換及其逆-1來計算，先對塊按行做一維離散傅里葉變換，再對結果按列重復操作；逆-1即先按列再按行做傅里葉變換。卷積滿足

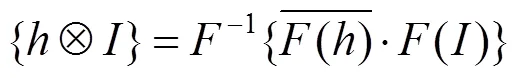
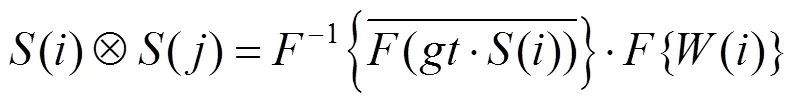
其中，為高斯加權函數；()為搜索窗口內的圖像；令=+，即為搜索窗口內的位移。()和()像素值的平方差可以通過位移表示，因此權重函數可以表示為

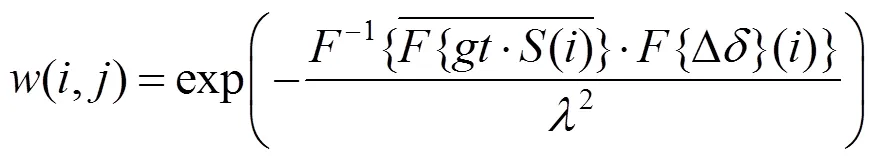
2.3 F-ANLM去噪算法

F-AMLN算法在仿射變換和仿射不變相似性度量上進行優化，加快了運行速度，算法步驟如下：

步驟1.輸入干凈圖像，添加白高斯噪聲，得到噪聲圖像；

在解決科學問題或社會挑戰的同時，會聚研究往往融合各學科特點形成新的創新方式，或開發新的科技產品，從而更好地推動創新模式和創新經濟的發展。

步驟2.將圖像分成31×31的矩形塊，利用sobel算子求梯度圖像，再求取每個像素點的結構張量()；

步驟3.對()進行奇異值分解，得到特征值和對應的特征向量，由特征值計算得到橢圓協變區域的長短軸，形成以為中心的橢圓圖像塊；

步驟4.利用像素點的自相關矩陣()1/2對橢圓圖像塊進行歸一化，使橢其變為固定半徑圓形圖像塊W，利用雙線性插值法進行像素插值；

步驟5.計算圓形圖像塊S的結構張量，奇異值分解后得到最大特征值所對應的特征向量,1，通過反正切函數得到旋轉角度θ；

步驟6.將圓形塊S旋轉θ度，使得仿射協變區域具有旋轉不變性；

步驟7.將中心塊和相似圖像塊之間的距離寫成離散卷積形式，計算高斯核函數；

步驟8.分別計算以像素點為中心的圓形圖像塊和以為中心的相似塊的平方和；

步驟9.使用DFT和IDFT對圓形塊在傅里葉變換域中執行一個逐項相乘和2個2D-FFT操作，快速實現卷積運算；

步驟10. 計算權重函數得當前像素點估計值。

3 實驗及結果分析

為驗證本文算法的可行性和有效性，從運行時間和去噪效果2個角度設計實驗。其中時間是使用Python自帶的計時器進行計時，去噪效果評價標準采用的是峰值信噪比PSNR，實驗環境為Python 3.7。測試圖片采用4張灰度圖像(lena，house，peppers，monkey)，通過對原圖添加白高斯噪聲，檢測算法在不同的噪聲等級和圖像下的去噪能力及用時。由仿射非局部均值算法經驗可知，當參數=31，max=5，=11時算法去噪效果較好，因此實驗采用此參數作為標準進行實驗，有

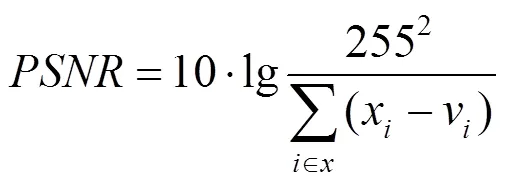
3.1 快速仿射非局部均值

首先，通過第一組實驗來是驗證F-ANLM的去噪性能。將原始NLM、ANLM和本文F-ANLM進行對比實驗，圖2為噪聲指數是30時的3種算法去噪效果圖；表1驗證了3種算法在不同圖像和噪聲等級下的PSNR (peak signal noise ratio)值。

圖2 3種算法的去噪效果圖

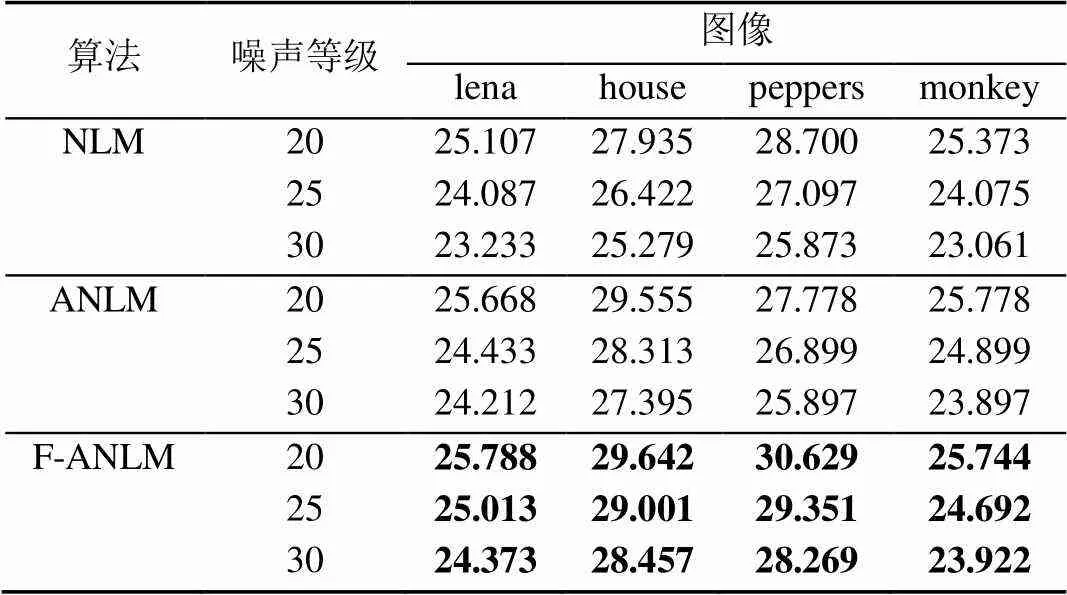
表1 3種算法在不同噪聲等級下PSNR值

從實驗結果可以看出，在圖像去噪質量上，本文算法未損耗ANLM算法的去噪性能。

3.2 比較R和D的用時情況

以lena圖(512×512)和house圖(256×256)為例，將本文算法中仿射變換和仿射不變相似性度量在不同噪聲等級下的用時與ANLM進行比較，其變化趨勢如圖3，4所示。

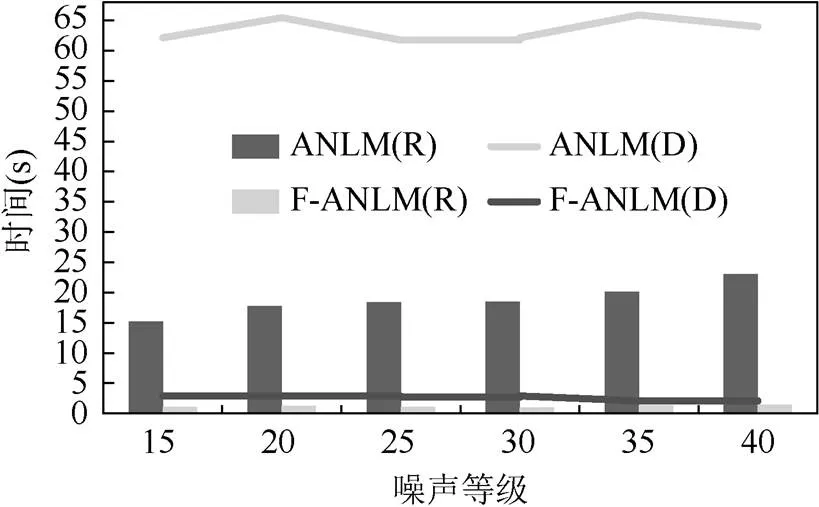
圖3 Lena算法用時變化趨勢圖

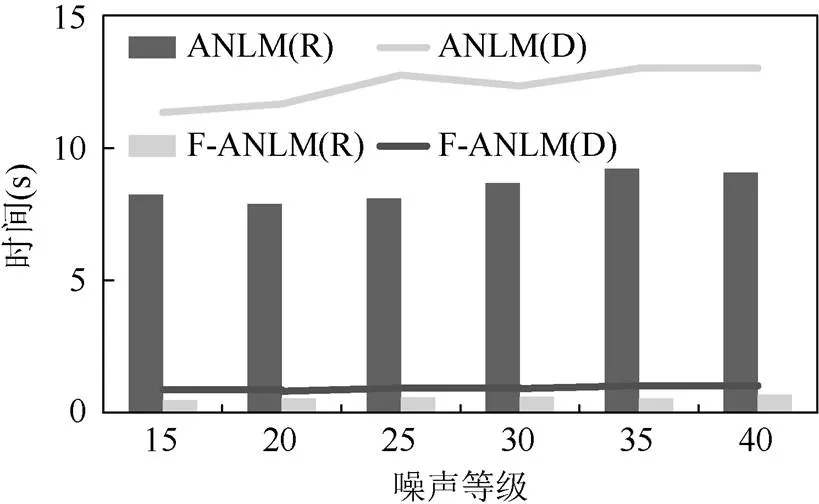
圖4 House算法用時變化趨勢圖

圖3和圖4的柱狀圖表示lena和house圖在ANLM和F-ANLM算法中仿射變換的運行時間，折線圖為仿射不變相似性度量的運行時間。綜合比較運用結構張量計算旋轉角度的時間比SIFT快約10～15倍，運用FFT計算相似度的速度大約提升13～20倍。

3.3 比較不同尺寸的圖像對速度的影響

從上述實驗可以看出，本文算法的速度受噪聲等級影響較小，變化趨勢不明顯。研究發現，運行速度受圖像大小影響較大，時間比率隨著圖像大小的增大而增大，圖像大小在500×500以下時，速度提升不明顯，但大于500×500時，本文算法性能體現出了明顯的優勢。為驗證此結果，選取128×128，256×256，512×512，750×750和1024×1024的圖片各5張進行實驗，噪聲等級=25，取每種尺寸圖像運行時間的平均值進行對比，實驗結果見表2。從結果可以看出，2種算法的時間比率隨著圖像尺寸的增大而增大。

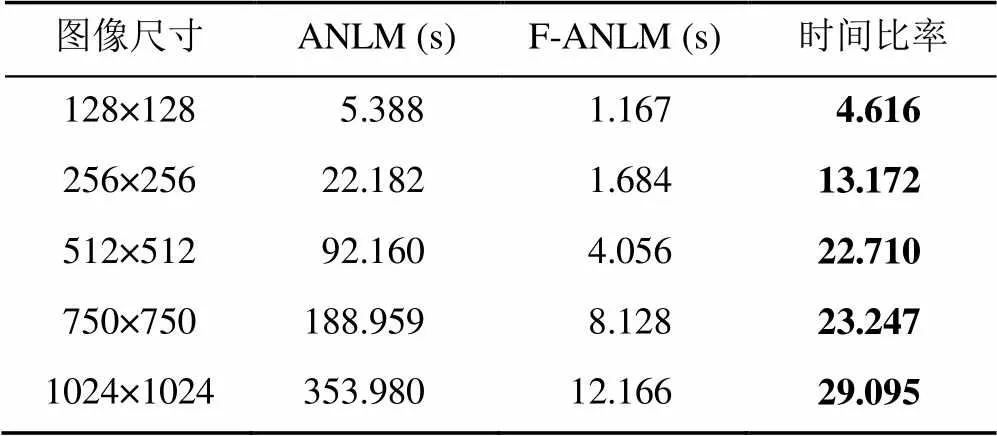
表2 2種算法在各尺寸下的運行時間

4 結束語

本文在ANLM算法基礎上，從減少運行時間的角度出發，對其2個部分進行了改進。首先簡化仿射變換，使用仿射協變結構張量特征向量的夾角來替換SIFT算子進行主方向的計算，然后將仿射不變相似性度量改寫成離散卷積的形式，使用FFT對其進行加速運算。實驗結果表明，本文提出的F-ANLM算法對基于仿射非局部均值算法加速方法具有可行性，在不損耗ANLM性能的基礎上速度提升的很快，效果極佳。

[1] BUADES A, COLL B, MOREL J M. A review of image denoising algorithms, with a new one[J]. Multiscale Modeling & Simulation, 2005, 4(2): 490-530.

[2] ZHAN Y, ZHANG X M, DING M Y. SUSAN controlled decay parameter adaption for non-local means image denoising[J]. Electronics Letters, 2013, 49(13): 807-808.

[3] ZENG W L, LU X B. Region-based non-local means algorithm for noise removal[J]. Electronics Letters, 2011, 47(20): 1125-1127.

[4] 蕭澍, 胡靖, 王彥芳. 橢圓窗口和參數自適應的非局部均值算法[J]. 計算機輔助設計與圖形學學報, 2020, 32(1): 79-89.

XIAO S, HU J, WANG Y F. Non-local means with elliptical window and adaptive parameter[J]. Journal of Computer-Aided Design & Computer Graphics, 2020, 32(1): 79-89 (in Chinese).

[5] DELEDALLE C A, DUVAL V, SALMON J. Non-local methods with shape-adaptive patches (NLM-SAP)[J]. Journal of Mathematical Imaging and Vision, 2012, 43(2): 103-120.

[6] TIAN J, YU W Y, XIE S L. On the kernel function selection of nonlocal filtering for image denoising[C]//2008 International Conference on Machine Learning and Cybernetics. New York: IEEE Press, 2008: 2964-2969.

[7] 陸海青, 葛洪偉. 混合魯棒權重和改進方法噪聲的兩級非局部均值去噪[J]. 計算機工程與科學, 2018, 40(7): 1227-1236.

LU H Q, GE H W. Two-stage non-local means denoising based on hybrid robust weight and improved method noise[J]. Computer Engineering & Science, 2018, 40(7): 1227-1236 (in Chinese).

[8] FEDOROV V, BALLESTER C. Affine non-local means image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(5): 2137-2148.

[9] WANG J, GUO Y W, YING Y T, et al. Fast non-local algorithm for image denoising[C]//2006 International Conference on Image Processing (ICIP). New York: IEEE Press, 2006: 1429-1432.

[10] LIU Y L, WANG J, CHEN X, et al. A robust and fast non-local means algorithm for image denoising[J]. Journal of Computer Science & Technology, 2008(2): 270-279.

[11] ZUO C L, JOVANOV L, LUONG H Q, et al. Rotation invariant similarity measure for non-local self-similarity based image denoising[C]//2015 IEEE International Conference on Image Processing (ICIP). New York: IEEE Press, 2015: 1618-1622.

[12] BAGHAIE A, YU Z Y. Structure tensor based image interpolation method[J]. International Journal of Electronics and Communications, 2015, 69(2): 515-522.

Fast affine non-local means image denosing

CHEN Ling-ling, ZHOU Xu-dong, XIE Jia-cheng, LIU Qian

(School of Information Engineering, Yangzhou University, Yangzhou Jiangsu 225127, China)

To address the problem of high time consumption of the affine non-local mean (ANLM) algorithm in the denoising process, a fast affine non-local mean denoising (F-ANLM) algorithm was proposed. Through time analysis of the affine non-local mean algorithm, it was known that the two modules, the affine transformation and the calculation of the affine invariant similarity measure, were the most time-consuming. Therefore, the optimization strategy was proposed from these tworegards. The algorithm first employed the included angle of the feature vector of the affine covariant structure tensor instead of the main direction of the SIFT operator, and then rewrote the affine invariant similarity measure in the ANLM method into the form of discrete convolution. In addition, the Fast Fourier Transform was adopted to reduce the amount of convolution operation and accelerate the calculation of similarity measures between affine covariant feature regions. Experiments show that the F-ANLM algorithm can simplify the calculation of affine transformation and affine invariant similarity measures, and greatly increase the speed compared with the original ANLM algorithm.

non-local; structure-tensor; affine-invariant; convolution; similarity-measure; Fast-Fourier

TP 391

10.11996/JG.j.2095-302X.2021050762

A

2095-302X(2021)05-0762-05

2021-01-04；

2021-02-23

4 January，2021；

23 February，2021

國家自然科學基金項目(61801417)

National Natural Science Foundation of China (61801417)

陳玲玲(1994–)，女，江蘇鹽城人，碩士研究生。主要研究方向為模式識別與圖像處理。E-mail：729325664@qq.com

CHEN Ling-ling (1994-), female, master student. Her main research interests cover pattern recognition and image processing. E-mail：729325664@qq.com

周旭東(1979–)，男，山西長治人，副教授，博士。主要研究方向為機器學習、模式識別與圖像處理。E-mail：xdzhou@yzu.edu.cn

ZHOU Xu-dong (1979-), male, associate professor, Ph.D. His main research interests cover machine learning, pattern recognition and image processing. E-mail：xdzhou@yzu.edu.cn