隧道開挖影響下地層-基礎體系的接觸力學響應分析1)

洪學飛 張頂立 方黃城 房 倩 周墨臻 侯艷娟 孫振宇

(北京交通大學城市地下工程教育部重點實驗室,北京 100044)

引言

在地層條件軟弱、周圍建筑物繁多的城市環境中進行隧道的施工,不可避免需要穿越和鄰近施工,隧道施工擾動將對既有建(構)筑物的力學狀態產生較大影響,進而導致建筑物的沉降、變形,甚至發生破壞[1-3].在城市運行高可靠度的要求下,隧道施工引起既有結構的工程響應預測與安全控制問題受到眾多專家學者與工程人員的廣泛關注[4-5].淺埋大剛度基礎作為城市中低層民用建筑的重要基礎形式之一,在城市密集區隧道工程中較為常見.因此,準確預測淺埋隧道施工引起地層與基礎結構的工程響應具有十分重大的工程意義.

隧道施工引起的地層變形及其傳播是造成既有結構變形破壞的重要誘因,因此隧道開挖引起的地層變形預測問題一直受到人們的關注[6].在城市地層變形理論預測研究方面,目前相關學者采用虛像法[7-8]、Airy 應力函數法[9-10]、隨機介質理論[11-12]和復變函數法[13-16]來預測不同隧道收斂模式、含隧道襯砌及土體重力效應影響等復雜條件下地層的位移和應力,取得了諸多有價值的研究成果.借助保角映射,復變函數理論可將含復雜形狀洞室的半平面映射到像平面內的圓環域,建立邊界方程,并利用一般冪級數解法確定地層變形和應力,其求解過程規范、能有效解決含復雜幾何邊界和力學邊界的問題,因而被廣泛應用于巖土工程含隧洞問題的解析預測中.上述理論成果只針對隧道施工引起地層變形和應力的預測,尚沒有考慮既有結構的存在.

在隧道開挖引起周圍既有結構力學響應的理論研究方面,目前普遍采用溫克爾彈性地基梁模型考慮地層與既有結構間相互作用,將地層視為一系列屬性相同、彼此獨立的線性彈簧系統[17].Attewell等[18]將經典溫克爾地基梁模型引入新建隧道施工對既有管線的影響研究中;侯艷娟[19]基于溫克爾模型,結合等代荷載法將隧道開挖引起的基礎支承弱化等效為作用于梁(基礎)上的附加荷載,給出了既有基礎結構變形和內力的解答;Liu 等[20]采用溫克爾地基梁模型研究了新建隧道下穿施工既有隧道問題,考慮了隧道開挖的附加荷載效應與地基支承弱化效應,對既有隧道結構受力與變形進行了解析研究.為處理溫克爾地基模型無法考慮地層剪切特性的缺陷,相關學者通過新增剪切層的處理辦法,建立了雙參數Pasternak 模型和三參數Kerr 模型等新地基模型,并在隧道開挖對既有結構影響的理論研究方面取得了諸多成果[21-24].

總體來說,目前關于隧道施工影響下地層與既有結構相互作用的解析理論基本將土體簡化成彈簧系統,而采用連續介質地基模型并考慮地層與既有結構間接觸效應的解析理論鮮有報導.此外,城市隧道工程中地層與既有結構間存在復雜相互作用,其本質是多體接觸問題[25].因此,本文將基于線彈性連續介質地基模型,建立考慮多體接觸作用的地層?基礎體系力學響應解析預測方法,研究隧道正交下穿引起的地層?基礎體系接觸力學響應,以期為城市隧道下穿淺埋大剛度基礎工程的設計與施工提供初步參考.

理論分析的基本假定如下:

(1)基礎結構沿隧道軸向具有一定長度,問題可看成關于豎軸對稱的平面應變問題.將地層視為各項同性均勻線彈性半平面,忽略重力效應;考慮大剛度淺基礎,將基礎結構簡化為作用于地表的剛性體;

(2)地層與基礎結構間存在光滑接觸作用,僅考慮接觸面法向壓力;

(3)采用隧洞邊界均勻徑向位移u0的單圓收斂模式簡單考慮隧道開挖效應;

(4)考慮小變形的情況,忽略地層變形對隧道幾何形位及計算點坐標的影響.

為方便描述,本文做如下約定:采用統一直角坐標系xoy,坐標原點位于原始狀態下的接觸面中點,X軸、Y軸分別以向右、向上為正;變量 σ ?i,x中下標“i”代表其屬于第(i)部分解答,下標“x”為外法線方向,上標“～”表示σi,x的洞周邊界值.滿足此約定的變量主要包括:應力分量(σx,σy,τxy)以及位移分量(ux,uy);應力以壓為負,且不考慮接觸面承拉能力.

1 求解思路與力學模型

1.1 問題求解思路

依據基本假定,隧道開挖引起的地層?基礎體系力學平衡的演化過程如圖1 所示.首先,相比于無應力彈性半平面狀態(原始狀態),基礎單獨作用于地層表面達到一次平衡(初始狀態);接下來,基于初始狀態,于隧道邊界施加增量位移u0,一次平衡被打破并最終形成二次平衡(最終狀態).本文目標問題是確定最終狀態的力學響應,其關鍵是最終狀態接觸壓力的求解.由于最終狀態接觸力學響應是隧道開挖與接觸效應耦合作用的結果,難以直接確定,故導致常規求解思路面臨極大的困難.

圖1 目標問題的常規求解過程Fig.1 General solving process of the target problem

基于以上求解新策略,將原問題轉化為求解3 個子問題的過程,并通過疊加對應的三部分解來獲得最終解答(見圖1 和圖2).各子問題描述如下:

圖2 目標問題的求解新策略Fig.2 New solving strategy for the target problem

問題1:彈性半平面Z1表面作用剛性基礎,基礎上部作用均布荷載q,接觸范圍外地表為自由應力邊界.半平面Z1的應力與位移解答對應第一部分解.

問題2:含一圓形隧洞的彈性半平面Z2,其隧道邊界為均勻徑向位移邊界(值為u0),半平面表面為自由應力邊界.半平面Z2的應力與位移解答對應第二部分解.

問題3:以問題2 確定的地表豎向變形曲線為表面幾何邊界的彈性半平面Z3,其表面對稱作用剛性基礎,基礎上部作用均布荷載q,接觸范圍外地表為自由應力邊界.半平面Z3的應力與位移解答對應第三部分解.

1.2 力學模型建立

根據以上內容,針對本文待求的三個部分解答分別建立了以下力學模型.

圖3(a)為第二部分解的力學模型.E和μ分別代表地層的楊氏模量和泊松比;隧道埋深與半徑分別用h與R表示;u0為隧道邊界均勻徑向位移值.

圖3(b)為最終狀態的接觸分析模型.L代表基礎半寬度;其余符號含義見下文接觸壓力的理論推導部分.

圖3 力學分析模型Fig.3 Mechanical analysis models

圖3(c)為第一、第三部分解的力學模型.V(x)代表作用于地表的豎向分布荷載,其作用范圍為(x1,x2).

圖3(d) 為基礎結構的力學分析模型.Mf(x0),Qf(x0)分別代表基礎x0斷面處的彎矩和剪力.

接下來,基于以上力學模型,分別針對各部分解答展開理論推導,詳細推導過程見本文第2 章.

2 解析方法

2.1 隧道均布收斂下地層響應解答

基于圖3(a)所示力學分析模型,本文采用復變函數理論開展第二部分解答的推導.目前,相關學者已針對此類問題開展大量研究,本文直接引用相關成果[15,26-28].根據復變函數理論,地層應力與位移分量均可由復平面Z2內兩個解析函數φ1(z)和ψ1(z)表示,其中地層應力的表達為

地層位移可表示為

式中,z為復平面Z2內任意點,z=x+ iy;κ是材料常數,對于平面應變問題κ= 3?4μ,μ為地層泊松比;G為地層剪切模量,G=E/[2(1 +μ)];上標“—”表示對復數取共軛.

采用保角映射[13]ω(ζ)將物理平面Z2映射成象平面ζ內的內、外半徑分別為α,1 的單位圓環域

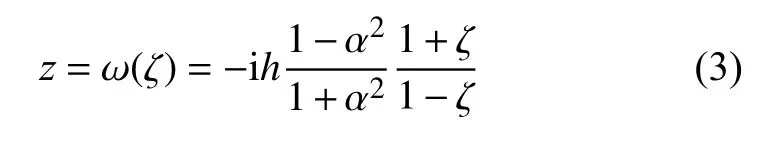
式中,α(0 <α<1)由方程R/h= 2α/(1 +α2)確定;ζ為單位圓環內任意點,ζ=ξ+ iη=ρeiθ,α≤ρ≤ 1.

利用式結合解析函數φ1(z),ψ1(z)中單值解析部分的Laurent 級數展開特性,得原解析函數在ζ平面內的表達如下

式中ak,bk,ck,dk及e0均為待定復系數.在計算過程中,φ(ζ),ψ(ζ)的ζ最高正(負)冪次分別取為N1,N1+ 2,因此解析函數中共有4N1+ 6 個待定復系數.

依據復合函數求導法則,解析函數φ1(z),ψ1(z)的各階導數在ζ平面內的表達式如下

本文采用基于頻域分析的求解方法來確定待定復系數,具體解析理論與求解過程可參考文獻[29-30].首先,利用單位圓環外邊界的自由應力條件建立兩個正交應力分量方程,并用單位圓環內邊界的切向、法向位移條件建立兩個正交位移分量的方程;然后根據頻域分析法,利用Fourier 變換將4 個邊界方程轉化到頻域中進行分析,取前N1+ 2 階頻率(不包括零階頻率)可建立含8N1+ 20 個方程的線性方程組;此外,取(± 100,0)作為地層豎向位移的零位移參考點來建立2 個附加方程;進而聯立8N1+ 22個線性方程確定4N1+ 6 個待定復系數;最后,將式(3)～式(5)帶入式(1)和式(2)分別確定第二部分解答中地層的應力分量(σ2,x,σ2,y,τ2,xy)和位移分量(u2,x,u2,y).

2.2 地層與基礎間接觸壓力解答

2.2.1 彈性接觸理論基本方程

在直角坐標系xoy下,根據彈性接觸理論[31],彈性半平面表面一定范圍內地層的受力與變形之間滿足關系

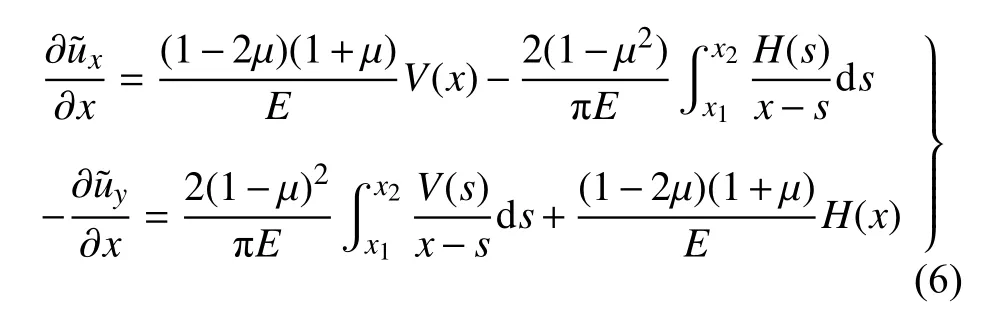
式(6)即為接觸控制方程.式中,H(x)和V(x)分別表示彈性半平面表面的水平和豎向分布力,其作用范圍為(x1,x2),方向分別沿X軸和Y軸正向;?u?x/?x和 ?u?y/?x分別表示接觸區間內地表水平位移梯度和豎向位移梯度;其余參數意義同上.

依據本文假定,考慮光滑接觸,第一部分解的核心是確定均布荷載q作用下地層與基礎間的接觸壓力p1(x),該問題與頂部光滑的剛性沖頭垂直壓入彈性半平面問題具有相同的解答,依據文獻[31],其接觸壓力p1(x)的解析式為

2.2.2 最終狀態接觸壓力p3(x)

由問題3 定義可知,需采用u2,y(x,0)曲線來刻畫半平面Z3表面幾何邊界.由于豎向位移u2,y(x,0)為級數解,為方便p3(x) 的數學推導,本文采用Sagaseta[7]建議的公式來描述由地層損失引起的地表沉降值,其表達式為

式中,Smax為最大地表沉降的絕對值;α1為待定的常數,本文中可通過接觸范圍內u2,y(x,0)的數值采用最小二乘法計算.

觀察圖3(b)中淺色部分基礎與地層間的幾何關系,結合式(8)不難看出基礎與地表間的間隙函數表達式如下

在接觸范圍(?L,L)內,基礎幾何邊界與地表豎向變形間存在如下幾何關系

式中,u3,y(x,0)為接觸范圍內地表豎向位移;δ2(δ2<0)為基礎豎向位移,此問題中為一常數.

依據假設,將式(8)～式(10) 帶入式(6),令H(x) = 0,得接觸壓力p3(x)的積分控制方程

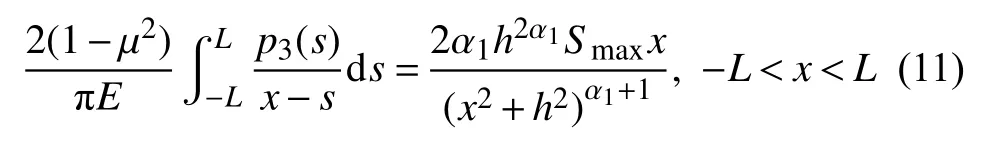
利用?=x/L,T=s/L及P(?) =p3(x)的代換將式(11)標準化,得

式(12)在T=?處奇異,本文直接引用該類“奇異積分方程”的相關成果[32],其解為

式中

忽略余項,考慮a>1 的情況,采用式中麥克勞林展開的前N2+ 1 項替代式(1 3) 中的f(T)=1/(T2+a2)α1+1部分,得

至此,P(?)表達式中只有常數C1未知.對式(11)而言,利用第一類奇異積分方程一般解可得p3(x)表達式中對應常數C2的結果,再結合代換?=x/L,P(?) =p3(x),建立常數C1和C2的關系式如下

考慮基礎結構豎向力平衡,有

聯立式(18)、式(19)求得C1,再將式(14)、式(15)及式(17) 帶入式(16) 確定P(?) 表達,最后結式P(?) =p3(x),最終得第三部分解中接觸壓力p3(x)的解析表達為式中各未知參數表達見前文,x∈(?L,L).

2.3 第一、第三部分解答

利用2.2 節中的式(7)和式(20)可分別確定地層?基礎體系的初始狀態接觸壓力p1(x)和最終狀態接觸壓力p3(x).接下來,通過Flamant 基本解的積分可計算地層中任意點的應力和位移分量值,進而獲得本文第一、第三部分解答.

地層中各點正應力與剪應力表達式為

各點位移表達式為

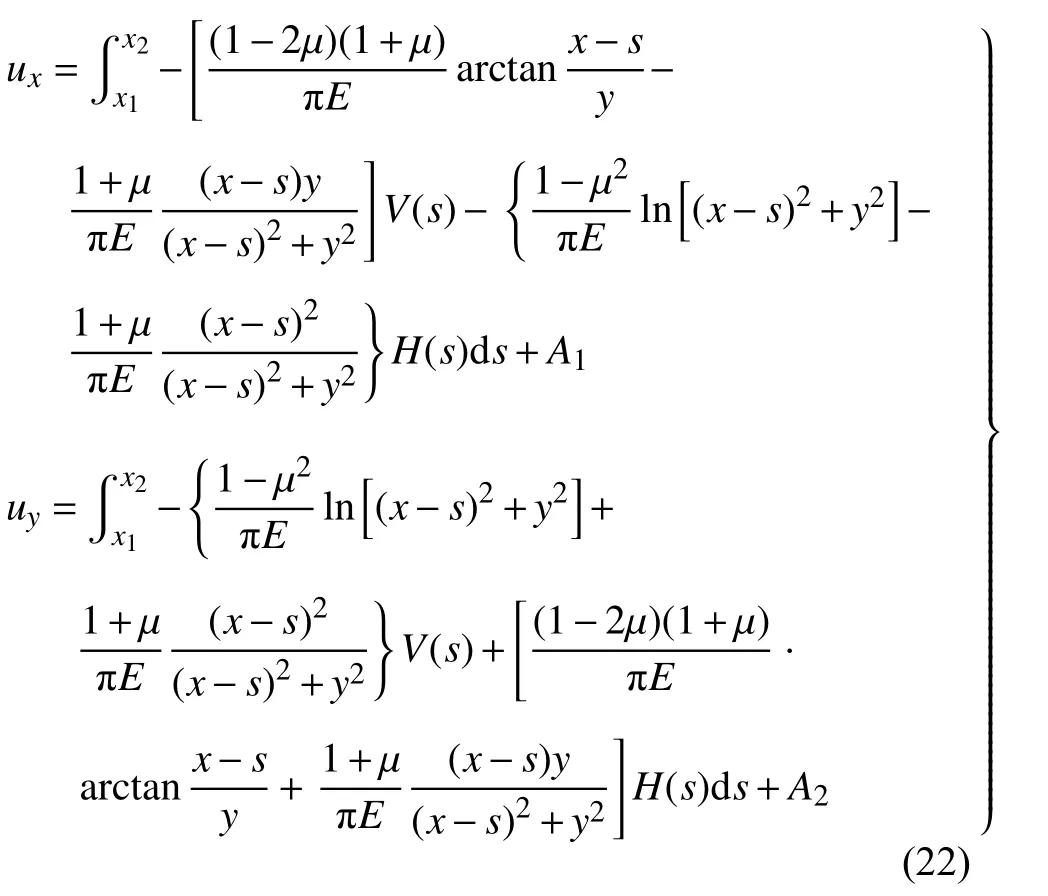
式中A1和A2分別表征水平和豎向剛體位移,需選定零位移參考點確定.依據問題對稱性,A1= 0,A2選定(?100,?200)點為豎向零位移點計算確定.

基于圖3(c)的力學模型,將式(23)帶入式(21)和式(22)可得第一部分解的應力分量(σ1,x,σ1,y,τ1,xy)和位移分量(u1,x,u1,y)

對于第三部分解的地層應力分量(σ3,x,σ3,y,τ3,xy)和位移分量(u3,x,u3,y),可通過將式(24)帶入式(21)和式(22)計算確定

2.4 最終狀態地層與基礎的響應解答

根據本文提出的目標問題求解新策略,采用等效狀態替代最終狀態,并疊加第二、第三部分解答確定等效狀態的應力與位移分量如下

工程中重點關注的由隧道開挖引起的地層與既有結構的附加位移為

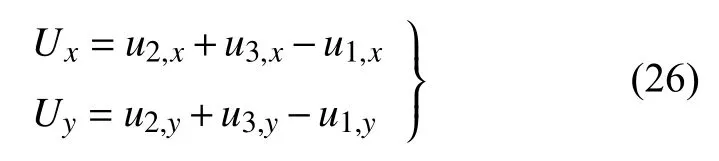
基于圖3(d)的力學模型,對基礎進行受力分析,得基礎x斷面處彎矩Mf和剪力Qf表達式如下

本文解析結果均依據上文解析方法采用程序計算確定,實際計算中為保證計算結果精度,取參數N1= 100,N2= 50.

3 解析驗證

為驗證本文解析理論正確性,引入ABAQUS 有限元軟件進行計算分析.按圖4(a)所示示意圖建立平面數值模型,該模型為由400 m × 200 m 的地層和20 m × 5 m 的基礎組成的整體,地層為均勻各向同性線彈性體,基礎為剛性體,地層與基礎結構間接觸采用ABAQUS 中計算精度高且穩定性好的“面對面接觸”算法模擬,接觸類型依據光滑接觸假定定義為無摩擦接觸.為優化數值計算精度與單元數量間匹配性,利用ABAQUS 非協調網格技術實現對隧道及基礎周圍地層單元的局部加密處理,并最終形成如圖4(b)所示的分區加密計算網格,其中各區域網格控制尺寸選定如下:區域1 網格控制尺寸(記為Ms)取0.05 m,區域2,3 分別取0.5 m,4 m.數值模擬過程分以下兩個步驟進行:第1 步,施加約束條件,并于基礎上表面作用豎向均布荷載q,計算保存;第2 步,在第1 步的基礎上,先凍結隧道邊界內單元,不考慮襯砌作用,并在隧道邊界上施加均勻徑向增量位移u0,計算最終狀態的力學響應.

圖4 數值模型的幾何示意和計算網格Fig.4 Geometric sketch and computational mesh of numerical models

本文所有計算模型及其對應的計算參數見表1,表中所有參數符號含義同上文,此外所有計算模型的隧道半徑R和基礎半寬度L分別取為6 m 和10 m.

表1 模型計算參數Table 1 Computational parameters of models

為較全面地分析、驗證解析方法的正確性,采用該方法計算表1 中第2,3 組參數模型解析解,同時借助ABAQUS 計算對應數值解,并重點對比分析了模型3 的地層位移場(ux,uy)以及不同參數下測線(L1,L2,位置見圖4(a))上各點豎向位移uy的解析解和數值解,結果示于圖5.

為方便對比分析,取位移分量與均勻徑向位移絕對值|u0|的比值,對位移進行歸一化處理.圖5(a)、圖5(b)分別給出了模型3 地層歸一化豎向位移場、水平位移場的解析解與數值解對比結果,可以發現位移解析解與數值解均關于Y軸對稱,兩者具有較高的吻合度.為探究不同參數下解析解的準確性,圖5(c)～圖5(f) 對比分析了不同泊松比μ與埋深h情況下地層歸一化豎向位移uy/|u0|的解析解和數值解,可以看出在參數改變時,解析解均保持較高的準確度.以上對比結果說明了本文新求解策略的合理性,同時也驗證了本文解析方法的正確性.

需注意,當泊松比較大或隧道埋深較小時,uy/|u0|解析解與數值解間的差異相對明顯(最大約2%),且數值上近乎相差一個常數(見圖5(c),圖5(f)),這是由積分法求解位移過程中“零”位移基準點選取的偏差造成的,但可以通過優化“零”位移基準點的選取來獲得精度更高的解答.對于一般情況,可以期望本文的解析理論給出較高精度的解答.

圖5 不同工況解析解與數值解對比分析Fig.5 Comparisons of analytical solution and numerical solution under different conditions

接觸力學響應無疑是接觸類問題的核心.在本文數值計算中,區域1 網格控制尺寸大小對計算結果精度具有較大影響.圖6 展示了在模型3 的參數條件下,改變Ms時接觸壓力的數值結果,同時給出了接觸壓力的解析值.從圖中局部放大部分可知,隨著Ms不斷減小,更精細的模型顯著提升了接觸壓力的計算精度,且數值解與解析解間的誤差也越來越小.因此,本文解析理論為此類問題接觸壓力的確定提供了一種準確、高效的計算方法,同時也為此類問題中地層與基礎結構相互作用的解耦分析提供了理論基礎.

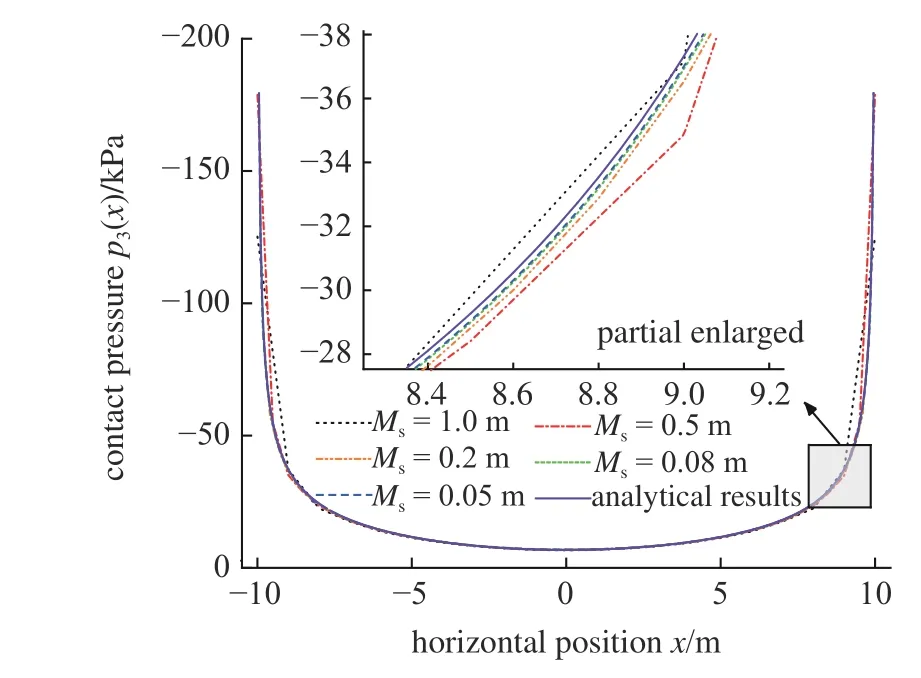
圖6 網格尺寸Ms 對接觸壓力計算結果的影響Fig.6 Influence of mesh size,Ms,on calculation results of the contact pressure

4 參數分析

實際工程中,地層與基礎間接觸壓力、基礎結構內力以及由隧道開挖引起的地層?基礎體系的附加位移等的分布是工程人員重點關注的內容,同時也是工前結構設計與施工中安全狀態評估的重要依據.基于本文解析方法,計算地層?基礎體系的接觸壓力p3(x)、地表附加豎向位移Uy(x,0)以及基礎結構彎矩Mf(x)和剪力Qf(x),并重點討論了地層楊氏模量E、地層泊松比μ、隧道埋深h、隧道邊界均勻徑向位移u0以及基礎外荷載集度q的影響.

4.1 地層參數的影響

地層作為向基礎結構傳遞隧道施工影響的關鍵媒介,其力學參數無疑對隧道施工擾動下地層?基礎系統力學響應有著重要影響.

(1) 地層楊氏模量E的影響

選取30,35,40,45 和50 MPa 五種地層楊氏模量,具體參數見表1 第1 組參數,計算結果示于圖7.從圖7 中可以看出,對于本對稱問題,接觸壓力、基礎彎矩分布均關于Y軸對稱,基礎剪力則關于原點呈中心對稱分布;基礎彎矩峰值位于基礎中點處,而基礎剪力峰值則對稱地出現在距基礎端部約0.3L位置處,因此工程中應注重滿足基礎中部抗彎能力及基礎端部附近抗剪能力的要求.具體到地層楊氏模量E的影響,觀察圖7(a)可以發現隨著E的增加,接觸壓力表現出基礎中部區域逐漸釋放、兩端進一步集中的變化規律,表明基礎受力狀態正在逐步惡化.不僅如此,楊氏模量的改變會進一步加劇基礎結構的內力集中.例如,對于Mf,當E= 30 MPa 時,基礎彎矩峰值為412.59 kN·m (x= 0 m);當E= 50 MPa時,基礎彎矩峰值為506.72 kN·m (x= 0 m),相比于30 MPa,基礎彎矩峰值增長了約22.8%.以上結果表明,楊氏模量的變化對地層?基礎體系接觸狀態和基礎結構受力狀態具有顯著影響.

圖7 地層楊氏模量E 的影響Fig.7 Influence of the Young’s modulus of stratum (E)

通過計算還發現,E的改變對地表附加豎向位移Uy(x,0)的分布幾乎沒有影響,但不同E對應的地表豎向位移uy(x,0)會有所差別.以上分析表明,地層楊氏模量的變化更傾向于造成接觸壓力和基礎內力的改變,而對地表附加豎向位移則影響甚微.

(2) 地層泊松比μ的影響

選取0.25,0.3,0.35 和0.4 四種地層泊松比,具體計算參數見表1 第2 組參數,主要計算結果如圖8所示.從圖中可以看出改變地層泊松比,Uy(x,0)和Qf的分布形態沒有變化,其中Uy(x,0)分布呈平底“V”型,并未呈現常規的槽型分布,表明接觸面附近地層附加豎向位移受接觸作用的影響顯著,且地表各點Uy(x,0)值整體上隨著μ的增大而減小(見圖8(a)).不同于地層楊氏模量的影響,地層泊松比μ的變化對Uy(x,0)的影響效果更明顯,而對接觸壓力和基礎內力分布的影響程度較小.以上結果表明,地層泊松比的改變對地表附加豎向位移具有一定程度的影響,但對接觸壓力和基礎受力的影響水平較低.

圖8 地層泊松比μ 的影響Fig.8 Influence of the Poisson’s ratio of stratum (μ)

4.2 隧道埋深h 的影響

地層變形向周圍傳播具有隨距離增大逐漸衰減的特性,因此隧道埋深與地層?基礎體系的力學響應密切相關.選取23,24,25,28 和30 m 五種隧道埋深,其余參數見表1 第3 組參數,計算結果見圖9.可以看出隧道埋深h對地表附加豎向位移Uy(x,0)的影響規律表現出區域差異性(見圖9(a)),在[?15,15]范圍內Uy(x,0)隨著h減小而增大,在此范圍外則表現出相反的變化規律.不僅如此,當h= 23 m時,觀察圖9(a)中有、無基礎情況下Uy(x,0)的分布可知,兩種情況下的Uy(x,0)值亦在[?15,15]范圍內差異明顯,此范圍外兩者的地表附加豎向位移值近乎相等.以上結果表明,地層變形是隧道開挖擾動與地層?基礎接觸效應耦合作用的結果,該耦合作用在遠離接觸區域時逐漸表現出隧道開挖擾動影響占主導地位的趨勢,由此可見基礎的存在對地層變形分布的顯著影響區域有限,驗證了本文采用等效狀態替代最終狀態的合理性.

對于接觸壓力p3(x) (見圖9(b)),相比于無隧道情況,隧道開挖擾動下的接觸壓力產生了顯著的中部釋放、端部集中的重分布現象,且其重分布程度隨著隧道埋深的減小而加劇,說明隧道施工擾動造成基礎接觸及受力狀態的惡化,這從基礎彎矩峰值的大幅增長可以看出(見圖9(c)).此外,隧道埋深減小將導致基礎中部接觸壓力值逐漸降為零,當接觸面無承拉能力時,地層?基礎體系將產生豎向位移不連續的脫空接觸現象,這是強烈的接觸作用結果,在地層?基礎體系力學響應的預測中應予以充分考慮.以上分析表明隧道埋深對地層?基礎體系各方面力學響應均有著顯著的影響.

圖9 隧道埋深h 的影響Fig.9 Influence of the tunnel buried depth (h)

4.3 洞周均勻徑向位移u0 的影響

洞周均勻徑向位移u0也直接決定了隧道施工擾動的劇烈程度.選定?20,?25,?30,?35 和?40 mm五種洞周均勻徑向位移,并與無隧道開挖情況計算結果作對比,具體計算參數見表1 第4 組參數.圖10(a)和圖10(b)分別繪制了Uy(x,0)和p3(x)的分布.對于地表附加豎向位移Uy(x,0),|u0|的增大導致地表各點處Uy(x,0)值的整體增大,這與前文h減小時所表現的區域性影響略有差別.對于接觸壓力p3(x),|u0|的增大與h的減小對p3(x)分布規律的影響相似,同時可以看出當|u0|增大到一定程度后亦會引起地層?基礎體系中部脫空接觸現象的發生.隧道邊界均勻徑向位移u0及隧道埋深h均與隧道施工擾動程度關系密切,因此兩者對地層?基礎體系力學響應的影響規律相似.

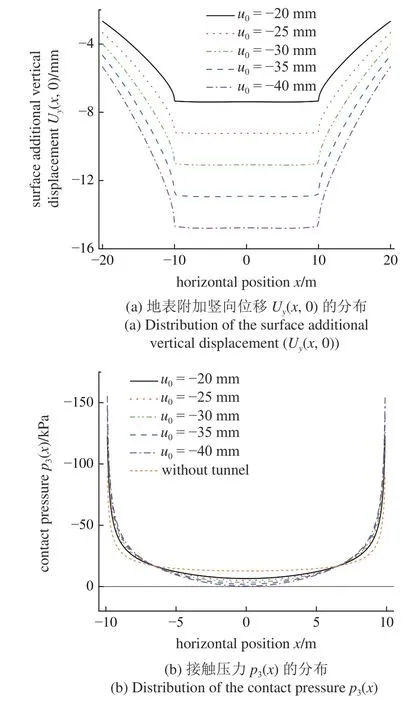
圖10 均勻徑向位移u0 的影響Fig.10 Influence of the uniform radial displacement (u0)

4.4 外荷載集度q 的影響

以上分析主要討論了地層物理力學參數及隧道相關參數的影響,本節考慮基礎上覆荷載集度q的影響.選定30,35,40,45 和50 kN/m 五種外荷載集度,其余計算參數見表1 中第5 組參數.圖11(a)繪制了僅改變q時接觸壓力的分布情況.從圖中可以看出,高荷載集度對應的接觸壓力整體量值大,但低荷載集度下接觸壓力中部釋放、兩端集中的程度更嚴重.觀察圖11(b),圖11(c)所示的基礎彎矩、剪力分布情況可知,雖然高荷載集度減弱了接觸壓力的重分布程度,但基礎內力仍表現出“集度高,內力大”的變化規律.

圖11 外荷載集度q 的影響Fig.11 Influence of the intensity of external loads (q)

此外,通過對Uy(x,0) 計算結果的分析發現:q的大小只影響地層豎向位移uy(x,0)的值,而對地表附加豎向位移Uy(x,0)則幾乎無影響(未畫出),該結果表明從源頭上控制隧道施工擾動可有效控制地層?基礎體系的附加位移響應,但高荷載集度下的變形控制措施要求更加嚴格.

5 結論

本文基于平面應變假設,將地層視為線彈性半平面,通過引入彈性接觸理論考慮地層?基礎體系的接觸作用,并針對接觸壓力求解這一核心問題提出了以“隧道開挖與基礎作用換序求解”為關鍵的新解析策略,最終建立了淺埋隧道開挖擾動下地層?基礎體系力學響應的耦合解析方法.通過解析解與ABAQUS 數值解對比結果的高度吻合驗證了該解析方法的正確性.基于此進行了影響因素分析,獲得以下主要結論:

(1)隧道開挖擾動對地層?基礎體系地表附加豎向位移、接觸壓力、基礎彎矩與剪力均存在不同程度影響.在接觸作用影響下,隧道開挖引起的地表附加豎向位移呈現平底“V”型分布,相比于傳統沉降槽分布表現出顯著的接觸相關性;接觸壓力發生不同程度的“中間釋放、端部集中”的重分布現象,并會造成基礎彎矩、剪力峰值的大幅增長,一定程度上劣化了基礎的受力狀態.

(2) 地層楊氏模量變化對隧道開挖引起的地層?基礎體系的接觸壓力和基礎內力有一定程度的影響,但幾乎不改變地表附加豎向位移的大小;與之相比,地層泊松比的影響則更側重于地表附加豎向變形的改變,而對接觸壓力和基礎內力的影響甚微.

(3)隧道埋深和隧道邊界均勻收斂變形的改變直接決定隧道施工擾動的強弱程度,二者均對地層?基礎體系各力學響應有著顯著影響.當隧道埋深減小或隧道邊界均勻徑向收斂變形增大到一定程度時,強烈的接觸作用會造成地層與基礎間產生變形不連續的脫空接觸現象,同時伴隨著應力的高度集中,實際工程中應及時采取加固措施避免此類情況的出現;盡管高荷載集度可在一定程度上減弱接觸壓力“中部釋放、端部集中”的程度,但基礎內力仍表現出“集度高,內力大”的變化規律.

(4)本文解析方法可量化描述地層與基礎間的接觸力學行為,同時也為地層?基礎體系接觸壓力的預測提供了可靠的理論方法.研究成果為淺埋隧道正交下穿影響下地層?基礎體系的接觸力學行為描述及力學響應預測提供科學參考.