循環(huán)神經(jīng)網(wǎng)絡在智能天平研究中的應用1)

聶少軍 王 粵 汪運鵬,2) 趙 敏 ** 隋 婧 **

* (中國科學院力學研究所高溫氣體動力學國家重點實驗室,北京 100190)

? (中國科學院大學工程科學學院,北京 100049)

** (中國科學院大學人工智能學院,北京 100049)

引 言

隨著航空航天技術的不斷發(fā)展,高超聲速技術受到各個航空航天大國的廣泛關注和深入研究,其科學問題具有重要的戰(zhàn)略意義[1].對于高超聲速飛行器氣動外形布局設計和優(yōu)化問題,高精度氣動力測量試驗起到?jīng)Q定性作用.激波風洞測力試驗可以為高溫真實氣體效應的研究提供可靠的數(shù)據(jù),同時為我國高超聲速飛行器研究提供關鍵技術支撐.

目前,激波風洞測力試驗仍存在許多未解決的關鍵技術問題,這些問題導致激波風洞測力試驗成為一個具有挑戰(zhàn)性的研究課題[2-4].最重要的問題之一是模型測力系統(tǒng)(force measurement system,FMS)受瞬態(tài)流場起動沖擊引起的結構慣性振動.在進行測力試驗時,由模型?天平?支撐構成的測力系統(tǒng)受到瞬時沖擊而產(chǎn)生結構振動,這些振動信號在短時間內(nèi)無法快速衰減,導致測力系統(tǒng)的輸出信號中包含慣性振動產(chǎn)生的干擾信號,嚴重影響測力試驗的精準度[5].

為了解決短試驗時間內(nèi)激波風洞高精度測力問題,國內(nèi)外學者開展了許多相關研究,發(fā)展了多種類型的脈沖型風洞天平,如壓電天平、加速度計天平、應力波天平、補償型天平和脈沖型應變天平等.在上述天平測力技術中,采用壓電陶瓷的壓電天平穩(wěn)定性相對較差,電荷泄露導致衰減相對較快,提高測量精度非常困難[6-7].加速度計天平[8-11]和應力波天平[12-15]試驗裝置成本較高且數(shù)據(jù)處理方法比較復雜.補償型天平只能對信號中的主頻分量進行補償,無法改善非主頻分量,所以其精度有待進一步提高[16].應變天平剛度較低,不能直接應用于激波風洞這類脈沖型設備中.脈沖型應變天平在應變天平的基礎上進行了改善,提升了天平的剛度,能夠在較短的有效試驗時間內(nèi)獲得多個周期的信號,但仍無法擺脫系統(tǒng)振動帶來的干擾[17-19].所以,為了滿足高超聲速飛行器高精度測力試驗的需求,發(fā)展測量精準度更高、頻率響應更快、穩(wěn)定性更強的新型測力系統(tǒng)很有必要,是研究激波風洞中影響測力結果的關鍵因素,其意義非常重大.

作為激波風洞測力試驗中的主要測量儀器,風洞天平的校準技術是測量試驗中確保天平性能的關鍵技術.一些學者將風洞天平的動態(tài)校準定義為在靜態(tài)校準的基礎上,利用飛行器測力標準模型在風洞中校驗天平性能[20].由于傳統(tǒng)風洞試驗中涉及到天平的動態(tài)性能研究不多,所以關于激波風洞測力天平動態(tài)校準方面的技術研究和工程應用比較少.目前,有學者提出基于深度學習技術的單矢量動態(tài)自校準(single-vector dynamic self-calibration,SVDC)方法并應用于脈沖型風洞測力系統(tǒng)中,在其動態(tài)天平信號樣本訓練過程中已經(jīng)成功將卷積神經(jīng)網(wǎng)絡(convolutional neural network,CNN)模型應用于天平測量結果的智能化處理,得到了較為理想的氣動力載荷結果[21].基于深度學習技術的風洞天平動態(tài)校準技術比較新穎,目前處于初步研究階段.

本文在SVDC 方法的基礎上,尋求新的有效訓練模型,探索各個模型間的差異,進一步提高智能型天平的數(shù)據(jù)處理性能及其應用的可靠性.在神經(jīng)網(wǎng)絡模型的選取上,首先利用循環(huán)神經(jīng)網(wǎng)絡(recurrent neural network,RNN)對激波風洞中的測力系統(tǒng)進行人工智能建模,識別并濾除測力系統(tǒng)中的慣性振動干擾信號,力求輸出較為理想的氣動載荷信號.將RNN 模型與CNN 模型訓練的結果進行對比,為風洞天平的高精度動態(tài)校準方法提供可靠的數(shù)據(jù)支撐.

1 RNN 在天平動態(tài)校準中的應用

1.1 單矢量動態(tài)校準技術簡介

傳統(tǒng)的風洞天平一般采用階躍響應法進行動態(tài)校準,即通過負階躍載荷單元加載方法對其施加動態(tài)激勵進行校準.該方法只能在固定的加載方向上對天平進行動態(tài)標定,每次標定試驗時在該方向通過懸掛砝碼的方式加載,待天平結構穩(wěn)定后,瞬間卸載產(chǎn)生階躍載荷,從而實現(xiàn)對天平施加負階躍載荷[22-25].這種動態(tài)標定的方法存在一定的局限性,對載荷施加方向有嚴格要求.為了滿足天平在任意方向?qū)崟r輸出多分量載荷信號,發(fā)展了單矢量動態(tài)自校準技術[21].該技術中“單矢量”并不是指輸出的通道為單一方向載荷信號,而是指在任意單一方向加載,該單矢量載荷可以沿著天平體軸系自動分解成可實時輸出的多分量載荷.

單矢量動態(tài)校準技術采用十字架懸掛鋼絲的方法激勵整個測力系統(tǒng),通過在任意方向懸掛鋼絲施加單矢量載荷,剪斷鋼絲瞬間卸載產(chǎn)生階躍載荷.在鋼絲彈性極限和懸掛鋼絲十字架的范圍內(nèi),這種加載方法對載荷的施加大小、方向和作用點均無特殊限制.單矢量載荷的加載可以實現(xiàn)多分量階躍載荷同時精確加載,更符合實際風洞試驗中的氣動力加載方式,且精準度更高.單矢量動態(tài)校準詳細的實施步驟參見文獻[21].

1.2 基于RNN 的動態(tài)模型訓練

1.2.1 RNN 模型的構建

對于許多復雜的機器學習問題來說,特征提取是一件至關重要且非常困難的事情.傳統(tǒng)的機器學習方法采用人工提取特征,這種方法不僅需要花費大量的時間和精力,而且無法很好地提取實體中的特征.深度學習方法很好的解決了這個問題,通過堆疊多層非線性映射逼近復雜的函數(shù),自動地從原始數(shù)據(jù)中學習層次化的特征表示,并且利用這些組合特征去解決問題.深度學習最早應用于圖像識別,現(xiàn)在已經(jīng)推廣到機器學習的各個領域,如語音識別、音頻識別、自然語言處理等[26].

針對天平輸出信號中的振動干擾信號,在采集完大量樣本數(shù)據(jù)后,采用深度學習技術中的神經(jīng)網(wǎng)絡對其進行監(jiān)督學習,可以自動提取到振動干擾信號的基本特征,將這些基本特征自動組合成復雜特征,從而完成對天平干擾信號的識別.網(wǎng)絡結構,下標t和t?1分別表示當前時刻和上一時刻.從圖中可以看出,對于當前時刻t,隱藏單元ht共同接受當前輸入層數(shù)據(jù)xt和前一時刻的隱藏層狀態(tài)ht?1來產(chǎn)生輸出ot(output layer).隱藏層的回路提供了信息傳遞的通路,從而實現(xiàn)信息的存儲和依賴.RNN 由于自身網(wǎng)絡結構存在延遲器(retarder)構成回路,是一種強大的建模序列數(shù)據(jù)的神經(jīng)網(wǎng)絡,模型訓練通常采用基于時間的反向傳播算法(back-propagation through time,BPTT).

傳統(tǒng)的前饋神經(jīng)網(wǎng)絡同層神經(jīng)元之間沒有連接,無法處理含有時間序列的信息,因此在許多應用中存在局限性.RNN 是深度學習技術中常見的神經(jīng)網(wǎng)絡結構,其主要解決時序問題,處理和預測序列數(shù)據(jù),在RNN 模型中,網(wǎng)絡具有“記憶”功能,網(wǎng)絡結構每層之間的節(jié)點是有連接的,其中隱藏層(hidden layer)的輸入不僅包含輸入層(input layer)的輸出,還包含上一時刻隱藏層的輸出.圖1 展示了RNN 的

圖1 循環(huán)神經(jīng)網(wǎng)絡單元結構示意圖Fig.1 Diagram of RNN unit

由于天平的輸出信號本質(zhì)上是一個時序動態(tài)信號,包括加載前的零值信號和加載后的氣動力信號,根據(jù)作用時間可以判斷測力系統(tǒng)的受力狀態(tài),而RNN 模型擅長解決與時序相關的問題,故采用RNN模型對天平輸出信號進行動態(tài)校準訓練.

在實際訓練過程中,樣本序列過長會導致優(yōu)化時出現(xiàn)梯度消失和梯度爆炸的問題[27].長短時記憶網(wǎng)絡(long short-term memory,LSTM)的出現(xiàn)解決了該問題,LSTM 在RNN 的基礎上增加了“門”結構,并通過一些“門”結構有選擇性地影響循環(huán)神經(jīng)網(wǎng)絡中每個時刻的狀態(tài).實踐證明采用LSTM 結構的RNN 模型比標準的RNN 模型表現(xiàn)更好.同時,在標準的RNN 模型中,狀態(tài)的傳輸是單向的,每一層的狀態(tài)傳輸都是從前往后單向進行,然而在實踐中,當前時刻的輸出不僅和之前的狀態(tài)有關,也和之后的狀態(tài)有關,所以需要采用基于LSTM 的雙向循環(huán)神經(jīng)網(wǎng)絡(bidirectional long short-term memory,Bi-LSTM).

1.2.2 樣本采集與數(shù)據(jù)處理

采用RNN 訓練智能模型前,需要對擬標定測力系統(tǒng)采集足夠的動態(tài)信號訓練樣本.訓練樣本信號需要與實際風洞試驗中的天平信號具有相同的特征,需要包含系統(tǒng)振動干擾信號.基于SVDC 技術在風洞外搭建階躍載荷采集裝置,該裝置與激波風洞測力系統(tǒng)相同,由模型、風洞天平和支撐結構組成,其中模型采用半錐角為10°、長度為750 mm 的標準尖錐測力模型,天平采用三分量脈沖型應變天平,三分量依次為法向力Y、俯仰力矩MZ和軸向力X,支撐采用彎刀支撐結構,具體結構如圖2 所示.

圖2 階躍載荷采集裝置[21]Fig.2 Step load acquisition device[21]

本文基于已搭建完的階躍載荷采集裝置采集了120 組動態(tài)載荷信號樣本,用于RNN 模型訓練.由于受到階躍載荷加載裝置中鋼絲的強度限制,采集裝置的天平輸出信號相對于實際風洞試驗時的輸出信號比較微弱.為了確保訓練樣本和風洞試驗數(shù)據(jù)的一致性,在訓練模型時,統(tǒng)一對天平輸出信號進行標準化處理,將數(shù)據(jù)按比例縮放,統(tǒng)一映射到一個小的特定區(qū)間內(nèi).數(shù)據(jù)的標準化便于網(wǎng)絡模型的訓練,有利于模型收斂速度和計算精度的提升.在訓練結束后,為了便于驗證計算結果,再對數(shù)據(jù)進行逆映射處理.

在標準化處理數(shù)據(jù)時,采用線性轉化函數(shù)將天平的輸出信號值映射到[?1,1]之間,具體轉換函數(shù)為

式中x是原始數(shù)據(jù), m ax(|x|)是原始數(shù)據(jù)中絕對值最大的值,x?是標準化之后的數(shù)據(jù).逆映射轉換函數(shù)為

式中x′是將標準化后的數(shù)據(jù)逆映射得到的原始數(shù)據(jù).

因此,本文的基本思路就是將帶有慣性振動干擾的動態(tài)信號作為輸入樣本,理想階躍載荷作為目標輸出樣本,通過構建LSTM 和Bi-LSTM 模型訓練樣本,對樣本中的干擾信號進行學習,識別并濾掉干擾信號,從而輸出理想的氣動力載荷信號.然后將訓練后的模型應用于激波風洞測力試驗中,得到低慣性干擾或無慣性干擾的氣動力信號,進而確保測力結果的準確性.

2 RNN 動態(tài)校準模型的訓練結果及分析

2.1 模型訓練結果驗證

在RNN 訓練模型應用于激波風洞測力試驗之前,需要對智能模型進行測試,驗證模型的可靠性.在訓練模型前需要先打亂樣本順序,然后劃分為若干批,每一批包含部分樣本,因為隨機打亂后的樣本比排序后的樣本更接近真實的概率分布.將采集的120 組動態(tài)載荷信號樣本打亂順序后用于RNN 模型訓練,其中80%的樣本作為訓練集用來訓練模型和學習網(wǎng)絡參數(shù),20%的樣本作為驗證集進行驗證校準測試.將采集到的階躍載荷樣本作為輸入,其對應的理想階躍載荷作為目標輸出.選取其中任意一個樣本,將其軸向力通道載荷繪制成圖3 所示.

圖3 階躍載荷信號Fig.3 Step load signal

圖3 中虛線表示采集到的階躍載荷(輸入樣本),實線表示期望輸出的理想階躍載荷(目標樣本).該樣本的采樣時間為150 ms,理想階躍載荷前50 ms內(nèi)軸向力在0 N 附近小幅波動,在第50 ms 時發(fā)生階躍,邊沿觸發(fā)時間可以忽略不計,軸向力由0 N 突變?yōu)?.7 N 左右,在后100 ms 內(nèi)保持4.7 N 不變.

采用LSTM 和Bi-LSTM 模型訓練采集到的動態(tài)載荷信號,將輸入的訓練樣本信號與經(jīng)過網(wǎng)絡訓練后的3 個通道的信號結果進行對比.圖4 展示的是軸向力通道輸入信號與經(jīng)過LSTM 和Bi-LSTM模型訓練后的信號的對比結果.圖中虛線代表未經(jīng)網(wǎng)絡模型處理的輸入信號,實線和點劃線分別表示經(jīng)過LSTM 和Bi-LSTM 模型處理后得到的輸出信號,點線表示期望輸出的理想階躍載荷信號.

圖4 軸向力通道輸入信號與經(jīng)過網(wǎng)絡模型處理后信號的對比Fig.4 Comparison of the input signal and validation data by training model (axial force)

由圖4 可以看出,經(jīng)過網(wǎng)絡模型處理后的信號曲線與期望輸出的理想階躍載荷信號曲線基本貼合在一起,在前50 ms 內(nèi),LSTM 和Bi-LSTM 模型的處理結果均比較理想,將輸入樣本中的干擾信號基本除掉了.在第50 ms 時,載荷產(chǎn)生突變.在后續(xù)100 ms內(nèi),處理后的輸出信號基本保持為一個固定值,達到理想階躍載荷的穩(wěn)定狀態(tài).所以經(jīng)過循環(huán)神經(jīng)網(wǎng)絡模型訓練后的信號基本濾掉了大部分干擾信號,整體上滿足了理想階躍載荷的要求.

按照同樣的方式對天平法向力和俯仰力矩通道的樣本進行處理,將處理后的結果整理成圖5 和圖6 所示.由圖5 和圖6 可知,經(jīng)過LSTM 和Bi-LSTM 模型處理過后的信號符合理想階躍載荷的初始狀態(tài)和穩(wěn)定狀態(tài),而且邊沿時間足夠短.

圖5 法向力通道輸入信號與經(jīng)過網(wǎng)絡模型處理后信號的對比Fig.5 Comparison of the input signal and validation data by training model (normal force)

圖6 俯仰力矩通道輸入信號與經(jīng)過網(wǎng)絡模型處理后信號的對比Fig.6 Comparison of the input signal and validation data by training model (pitching moment)

經(jīng)過LSTM 和Bi-LSTM 模型訓練后的結果比較理想,濾掉了大部分振動信號,符合理想階躍載荷的要求,達到了預期目標.但是相比于LSTM 模型,Bi-LSTM 模型的訓練結果更好,尤其是在初始狀態(tài)和邊沿處,LSTM 模型處理的結果仍然存在一些干擾信號,Bi-LSTM 模型處理的結果更穩(wěn)定,更理想.

2.2 訓練結果誤差分析

在RNN 模型訓練過程中,通過最小化損失函數(shù)(loss)使模型達到收斂狀態(tài).本研究采用均方誤差指標(mean squared error,MSE)作為損失函數(shù)來評估模型的數(shù)據(jù)處理能力.MSE 指的是模型每一次輸出結果與模型輸出期望之間的誤差,MSE 的值越小,說明預測模型試驗數(shù)據(jù)的精確度越高.將LSTM和Bi-LSTM 模型的loss 值隨訓練輪數(shù)(epochs)的變化情況繪制成圖7 和圖8 所示.

圖7 和圖8 中虛線和實線分別代表模型訓練過程中的訓練誤差和驗證誤差.模型的初始loss 值在10?2量級,隨著訓練輪數(shù)的增加,模型的loss 值逐漸減小并趨于穩(wěn)定.當訓練輪數(shù)達到10 000 次時,LSTM 模型的驗證誤差值降到5.8 × 10?4,Bi-LSTM模型的驗證誤差值降到1.3 × 10?4.此時認為模型的誤差足夠小,已經(jīng)達到有效動態(tài)校準的標準,從而驗證了循環(huán)神經(jīng)網(wǎng)絡模型處理數(shù)據(jù)方法的可行性.根據(jù)模型訓練的loss 數(shù)據(jù),發(fā)現(xiàn)Bi-LSTM 模型比LSTM模型訓練效果更理想.

圖7 LSTM 模型loss 值隨訓練輪數(shù)的變化Fig.7 Loss changes with epochs in LSTM model

圖8 Bi-LSTM 模型loss 值隨訓練輪數(shù)的變化Fig.8 Loss changes with epochs in Bi-LSTM model

同時,為了評估訓練結果的好壞,可以采用相對誤差 δ 對訓練結果進行比較驗證.選取階躍載荷卸載后的數(shù)據(jù)進行分析,考慮到與激波風洞試驗實際有效時間相對應,對圖4～圖6 中經(jīng)過模型處理后的信號進行處理,截取時間區(qū)間為70～110 ms 內(nèi)的數(shù)據(jù)平均化處理得到近似值F?和真實值F,其中FL?和FB?分別代表LSTM 和Bi-LSTM 模型訓練得到的近似值,根據(jù)相對誤差的定義式(3)計算得到相對誤差δ ,δL和 δB分別表示LSTM 和Bi-LSTM 模型訓練得到的相對誤差,將計算結果整理成表1 所示

表1 的數(shù)據(jù)是LSTM 和Bi-LSTM 模型經(jīng)過訓練后的輸出信號與理想輸出信號之間的相對誤差值,兩個模型訓練的相對誤差值均比較小,LSTM 和Bi-LSTM 模型的相對誤差 δL和δB分別在3% 和0.3%以內(nèi),與文獻[21]中采用CNN 模型訓練得到結果的相對誤差(1%以內(nèi))相當,精準度均比較高,且軸向力信號的相對誤差明顯小于其他兩個載荷分量的誤差.原因是在采集訓練樣本過程中,軸向力的值比較大,占主導地位,其他兩個分量的值比較小,受到外界環(huán)境噪聲的干擾比較大,所以軸向力的結果相應比較理想.同時,根據(jù)表1 中 δL和 δB的數(shù)據(jù),發(fā)現(xiàn)在輸入樣本訓練過程中,Bi-LSTM 模型的訓練效果較LSTM模型的訓練效果更精確.

表1 LSTM 和Bi-LSTM 模型的相對誤差Table 1 Relative error of LSTM and Bi-LSTM model

3 脈沖風洞瞬態(tài)測力試驗數(shù)據(jù)的智能化處理

3.1 RNN 模型應用于激波風洞測力系統(tǒng)

經(jīng)過對LSTM 和Bi-LSTM 模型訓練結果的驗證分析,發(fā)現(xiàn)模型對輸入樣本中慣性振動干擾信號的處理非常理想,因此嘗試將該模型應用于激波風洞試驗智能天平的動態(tài)校準研究中.自中國科學院力學研究所成功研制復現(xiàn)高超聲速飛行條件激波風洞(簡稱“JF-12 復現(xiàn)風洞”)以來,在該風洞中完成了大量的高超聲速飛行器氣動力測量試驗,并獲得了大量高精度的可靠測力數(shù)據(jù)[28].JF-12 復現(xiàn)風洞采用反向爆轟驅(qū)動技術[29],同時集成應用一系列的延長試驗時間的創(chuàng)新技術[30-32],擁有復現(xiàn)25～50 km 飛行高度,馬赫數(shù)5～9 的純凈空氣氣流能力,有效試驗時間超過了100 ms.本研究利用LSTM 和Bi-LSTM 模型對在JF-12 復現(xiàn)風洞中進行的750 mm標準尖錐模型測力試驗中的三分量天平輸出信號進行處理,將軸向力通道的處理結果展示在圖9 中.

圖9 中虛線代表風洞試驗中天平輸出的原始信號,實線和點劃線分別代表經(jīng)過LSTM 和Bi-LSTM 模型處理后的輸出信號,可以發(fā)現(xiàn)處理后的信號基本濾掉了大部分振動干擾信號,但是仍然表現(xiàn)出一定的周期性.在模型訓練過程中,由于輸入樣本與風洞試驗測力信號存在一定的區(qū)別,而且風洞試驗中的真實氣動力信號并不完全是理想的階躍載荷信號,所以處理過后的信號與理想階躍載荷信號仍存在一定的偏差.在下一步模型訓練中,可以考慮增加訓練樣本數(shù)目,同時在采集樣本的過程,適當消除環(huán)境噪聲的干擾,最大程度的保證采集樣本與風洞試驗測力信號的一致性,從而提升模型處理樣本的能力,獲得更高精度的結果.

圖9 軸向力通道風洞試驗信號與模型處理的信號Fig.9 Wind tunnel test signal and model processed signal (axial force)

按照同樣的方式將法向力通道和俯仰力矩通道的處理結果整理成圖10 和圖11 所示.經(jīng)過LSTM和Bi-LSTM 模型處理后的結果與風洞試驗信號存在明顯的區(qū)別,基本將風洞試驗信號中的振動干擾信號去除掉,達到了預期目標.

圖10 法向力通道風洞試驗信號與模型處理的信號Fig.10 Wind tunnel test signal and model processed signal (normal force)

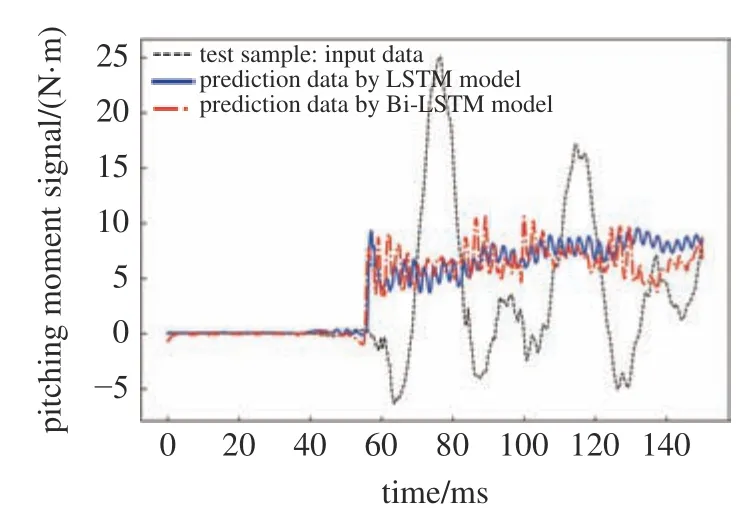
圖11 俯仰力矩通道風洞試驗信號與模型處理的信號Fig.11 Wind tunnel test signal and model processed signal (pitching moment)

3.2 RNN 與CNN 訓練結果對比

對風洞試驗測力信號進行誤差分析,將經(jīng)過RNN 模型處理后的結果與文獻[21]中經(jīng)過CNN 模型處理后的結果進行對比,對圖9～圖11 中經(jīng)過模型處理后的信號進行處理,截取時間為70～110 ms內(nèi)的數(shù)據(jù)進行平均化處理,將結果整理至表2 中, δL和 δB分別表示風洞試驗信號經(jīng)過LSTM 和Bi-LSTM模型訓練后得到的相對誤差.對比發(fā)現(xiàn)LSTM 與CNN 模型的誤差在4%以內(nèi),Bi-LSTM 與CNN 模型的誤差在2%以內(nèi),表明基于RNN 和CNN 模型的智能校準方法均具有較高的可靠性.此外,CNN模型常用于圖像識別,處理空間信息,RNN 模型通過挖掘數(shù)據(jù)中的時序信息,更適合處理解決時序問題,兩種神經(jīng)網(wǎng)絡模型在脈沖風洞瞬態(tài)測力試驗中均具有應用前景.

表2 RNN 與CNN 模型處理數(shù)據(jù)的相對誤差Table 2 The relative errors of RNN and CNN models in processing data

由于訓練樣本信號與風洞試驗信號存在一定的差別,真實氣動力信號較理想階躍載荷信號更為復雜,因此盡管采用LSTM 型和Bi-LSTM 模型訓練的采集樣本驗證結果十分理想,但是將模型應用于風洞試驗測力信號中仍存在一些偏差.就目前基于RNN 模型的激波風洞智能天平研究結果而言,該智能動態(tài)校準方法在激波風洞測力試驗中具有應用價值,采用該技術方法處理的測力結果的精準度具有較大提升空間.

4 結 論

為了在激波風洞短試驗時間內(nèi)開展高超聲速飛行器模型的精確氣動力測量,本文在單矢量動態(tài)自校準技術的基礎上,在動態(tài)信號訓練過程中采用了RNN 對激波風洞測力系統(tǒng)振動特性進行了高效建模,智能模型有效地去除了動態(tài)測力信號中的慣性干擾信號,輸出了“定常”的氣動力載荷信號.對采用RNN 模型的動態(tài)校準方法進行了誤差分析,并將該方法與基于CNN 模型動態(tài)校準方法進行了對比,驗證了該方法的可靠性.將RNN 模型動態(tài)校準方法應用于激波風洞測力系統(tǒng)中,基本消除了天平輸出信號中的大幅振動干擾信號,取得了較為理想的效果.

目前,基于人工智能技術的測力天平智能化研究比較新穎,相關方法和技術在具有可行性和可靠性基礎上有待進一步發(fā)展和完善.本研究進一步驗證了該方法的實用性,證明該方法在激波風洞測力試驗中具有應用前景,其將為我國高超聲速飛行器高焓氣動特性精確評估提供關鍵技術支撐.