道路微波除冰中微波輻射端口高度仿真與試驗研究

陸 松， 孔令揚， 杜 鵑

(1.空軍工程大學航空工程學院， 西安 710038； 2.西部戰區空軍勘察設計院， 成都 610041；3.四川云景通航工程設計有限公司， 成都 610094)

中國地域遼闊，氣象條件復雜，北方一些地區長時間處于冬期，一些高海拔地區也是長年處于冰凍期[1]。由于長時間低溫影響，道面上殘留雨水凝結成冰層，大幅降低道面摩擦因數，給交通安全帶來較大壓力。目前，除冰作業中常用的三類除冰方法[2-4]有清除法、融化法和抑制法，對于清除道面積冰發揮了一定作用，但在使用中也存在一些問題，比如高溫氣流對道面傷害大、能源利用率低、環境污染嚴重等。因此，為適應新時期道路交通的發展需要，提升道路保障性能，研發一種新型除冰方法勢在必行。

微波除冰技術是近年發展起來的新型除冰技術，相對于傳統除冰方法，它具有較多優點：冰層除凈率高、厚冰清除效果好、綠化環保等，在道路冬季除冰中具有較好的應用前景。微波除冰方法從20世紀70年代就被提出，但是實際工作中一直未得到推廣應用，這主要是由于微波除冰效率太低，難以滿足實際工作中除冰作業的需要[5-6]。因此，為了改善微波除冰方法的除冰效率，中外研究人員對微波加熱技術和微波除冰效率進行大量研究。國外方面，美國聯邦公路局實施的公路戰略研究計劃項目(strategic highway research program，SHRP)[7]中，Lindroth等[8]、Ye等[9]、Gao等[10]以及美國明尼蘇達州的自然資源研究所(natural resources research institute，NRRI)組織[11-12]等都對微波除冰技術都進行了深入研究，但由于微波除冰效率較低，在實際作業中應用較少。國內對微波除冰技術也進行了一定研究，但是大部分都側重于開發微波加熱裝置，而對微波加熱機理研究比較少[13-15]。2003年，李笑等[16]、關明慧等[17]在國內首次提出了利用微波加技術進行道路除冰的想法，設計了微波除冰車模型，同時申請了兩項微波除冰的專利[18-19]。2012年，郭德棟等[20]采用具有極強微波吸收能力的磁鐵礦代替普通集料，研究了磁鐵礦瀝青混凝土材料的配比設計，微波與磁鐵礦的發熱機理，磁鐵礦瀝青路面的道路微波除冰效率及除冰工藝。2016年，陸松等[21]對機場混凝土道面微波除性能進行了研究，分析了微波頻率和道面材料特性對機場道面微波除冰效率的影響。總的來說，現有研究主要對微波除冰的材料、微波頻率、微波輻射器設計進行了研究，但對微波除冰方法在實際作用中的應用技術缺乏分析，這就要求必須對輻射端口高度進行深入研究，且部分研究采用的試驗設備比較簡單，缺乏系統設計。

為了有效提升冬季道路微波除冰效率，更好指導微波除冰技術的工程應用，現對微波輻射端口高度進行一定研究。由于微波場在除冰過程中的分布十分復雜，目前許多理論還無法給出精確的解析解。鑒于此，現以微波損耗能量方程和非穩態導熱方程作為理論基礎，以COMSOL Multiphysics軟件為平臺，建立微波除冰仿真模型，并結合微波除冰實際工程特點，自主設計專門的微波除冰試驗平臺。采用仿真與試驗相結合的手段研究端口高度與除冰效率的關系，確定最佳的輻射端口高度，為微波除冰技術在冬季道面除冰中的應用提供技術指導。

1 微波除冰機理分析

微波是一種特殊能源，對其電磁場中的介質具有加熱的特性，并且微波加熱介質的性能與介質的吸波性能有關。根據電磁波理論[22]，介質對微波的吸收性能以損耗角tanδ表示，物質對微波的吸收性能越強，tanδ越大。相關研究[23]表明，冰的損耗角只有0.000 9，遠小于混凝土的損耗角0.048。由此可見，冰層對微波的吸收性能非常弱，幾乎可忽略不計，表明冰層具有透波特性。微波除冰技術正是利用冰層的透波特性，使微波透過冰層與機場道面相互作用，將微波能量轉化為熱量，利用該熱量融化冰層與道面的粘結層，從而使冰層與道面發生脫離，這就是機場道面微波除冰機理。微波除冰的示意圖如圖1所示。

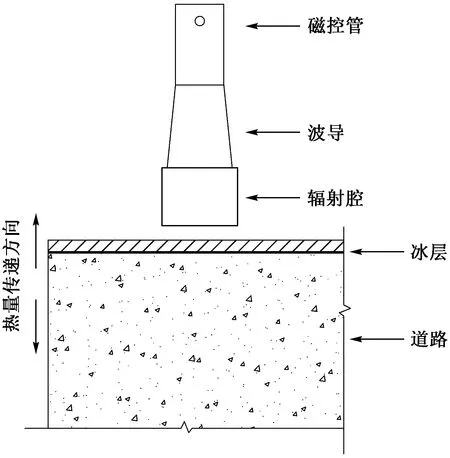
圖1 微波除冰示意圖Fig.1 Schematic diagram of microwave deicing

由圖1可知，將具有微波激發的輻射裝置置于道面冰層上后，微波會在輻射腔內激發后并向道面輻射。由于冰層吸收微波的能力較弱，微波會透過冰層直接作用在道面上，道面在微波作用下溫度不斷上升，從而在冰層與道面之間產生溫度差形成溫度梯度。在溫度梯度作用下，冰層會通過熱傳導方式不斷地從道面吸收熱量。冰層吸收熱量后，其溫度逐漸升高，導致冰層與道面之間的凍黏力逐漸減小。當冰層與道面之間凍黏層的溫度達到0 ℃時，凍黏層融化成水，此時，冰層就“浮”在道面上，再通過其他機械作用將冰層破碎并清除，這樣道面積冰就會比較容易被清除干凈。

2 仿真模型建立

根據微波磁-熱耦合理論分析可知，微波除冰理論模型是一組非線性偏微分方程，現有的數學理論無法完全從數學推導上得到其精確解。隨著計算機科學和數值計算理論的發展，可通過計算機建立仿真模型，采用有限元理論計算該模型。據此，以微波損耗能量方程和非穩態導熱方程作為理論基礎，選擇COMSOL Multiphysics軟件為平臺，建立微波除冰仿真模型。

2.1 模型建立

以單個磁控管為研究對象，以混凝土道面為例，建立微波除冰三維磁-熱耦合模型，模型中包括道面、冰層、磁控管、波導和微波輻射腔。道面模型尺寸為150 mm×150 mm ×150 mm，冰層模型尺寸為150 mm×150 mm×15 mm，并且其厚度可根據仿真的需要進行調節，輻射腔尺寸為150 mm×150 mm×150 mm，波導分為兩段，矩形段和喇叭輻射段，其中，矩形波導段尺寸為54.6 mm×95.3 mm，長度150 mm；喇叭輻射波導段寬口尺寸為54.6 mm×109.2 mm，長度為150 mm，輻射腔端口高度根據需要進行調整。同時，為了模擬無限空間微波的輻射情況，在模型中建立阻抗匹配層(perfectly matched layer，PML)，其尺寸為1 000 mm×1 000 mm×1 000 mm。

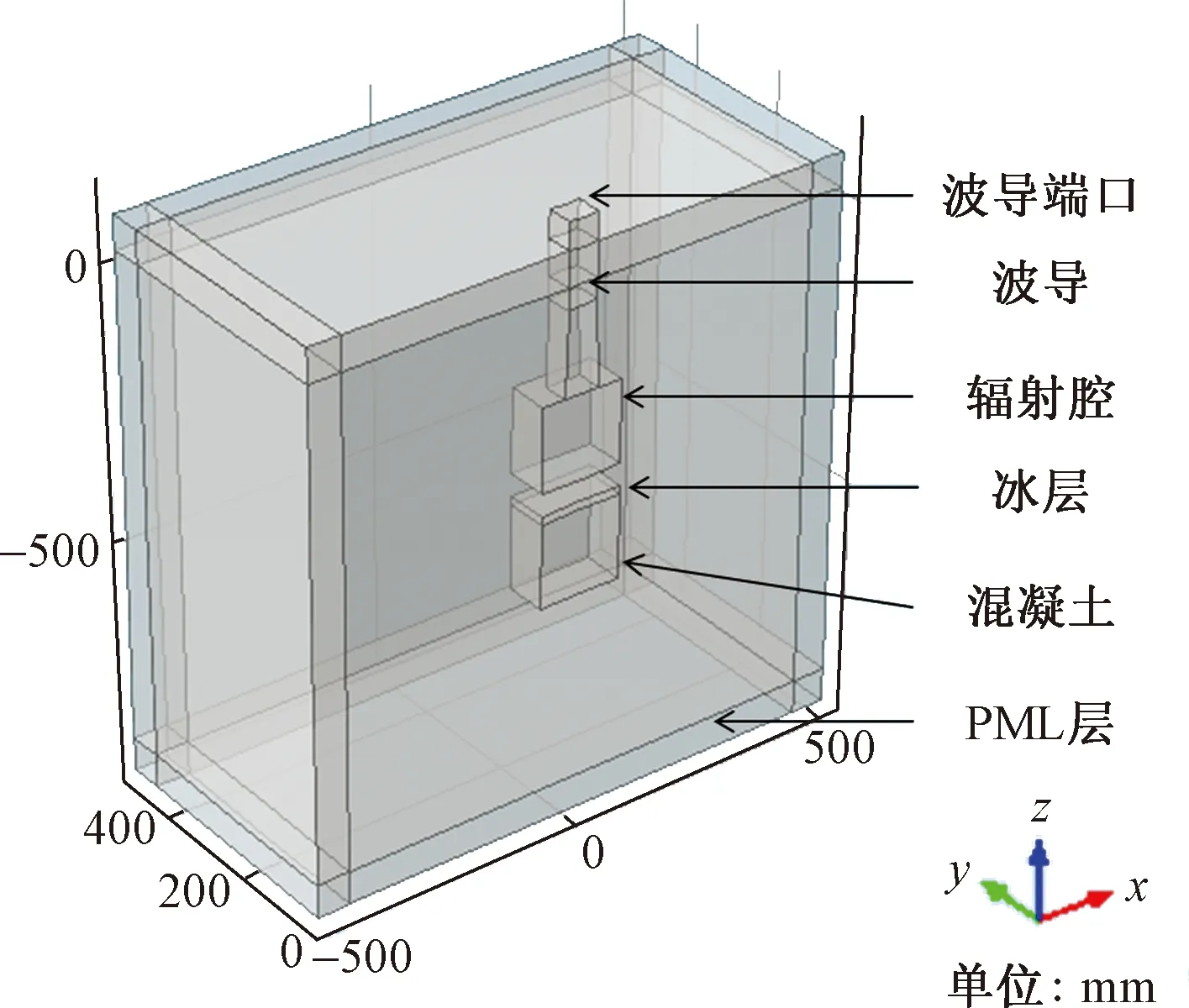
圖2 混凝土道面微波除冰模型Fig.2 Concrete pavement microwave deicing model

如圖2所示，喇叭波導端口長邊沿Y軸方向，短邊沿X軸方向，各坐標軸方向如示意坐標軸方向所示。為了節約仿真所需的內存及仿真運行時間，考慮到三維模型具有對稱性，以模型對稱面為界將模型分成兩部分，以其中一部分為研究對象，模型對稱面為“Y=0平面”，坐標中心設定在模型對稱面內矩形波導和喇叭輻射波導分界面中心位置。

2.2 參數設定

環境溫度設定為-10 ℃，且根據研究需要可更改，微波輸入功率為2 kW，頻率為2.45 GHz。各模型的物理屬性由其輸入參數確定，在三維磁-熱耦合模型中，模型的輸入參數主要包括電磁參數和熱力學參數。空氣的介電常數為1，其損耗很低，可忽略不計，模型中不考慮空氣的熱傳導效應，混凝土表面的換熱系數為4.74 W/(m2·K)，其他熱力學參數如表1所示。混凝土電磁參數：介電常數實部(ε′)為7.24，介電常數虛部(ε″)為0.44，介電常數損耗角正切(tanδe)為0.06，磁導率實部(μ′)為1.00，磁導率虛部(μ″)為0.02，磁導率損耗角正切(tanδm)為0.02。

在冰融化成水的相變過程中，存在潛在熱，即在0 ℃附近冰水混合物吸收大量熱量而溫度保持不變。在軟件固體傳熱模塊中嵌有相變傳熱物理接口，通過該物理接口可較好地模擬冰融化成水的相變過程。圖3為仿真得到的冰吸收熱量融化過程中的溫度變化，可以看出，在0 ℃附近有一段時間溫度保持不變。

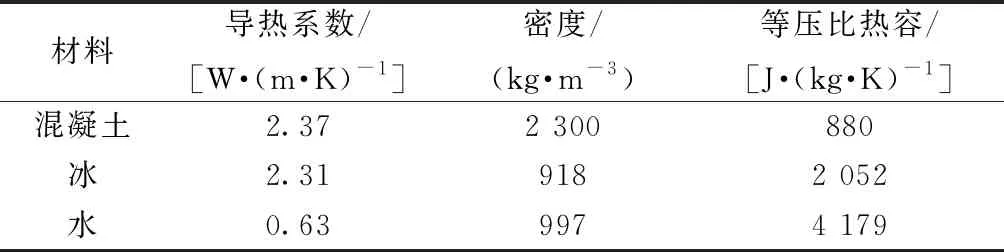
表1 模型中材料的熱力學參數Table 1 Thermodynamic parameters of materials in the model

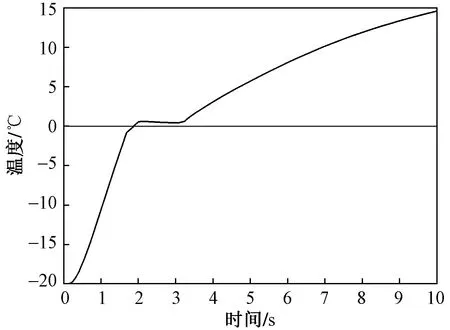
圖3 冰水相變過程中的溫度變化Fig.3 Temperature changes during ice-water phase transition

2.3 網格劃分

COMSOL Multiphysics為用戶提供了多種網格劃分技巧。本模型的網格劃分圖如圖4所示。

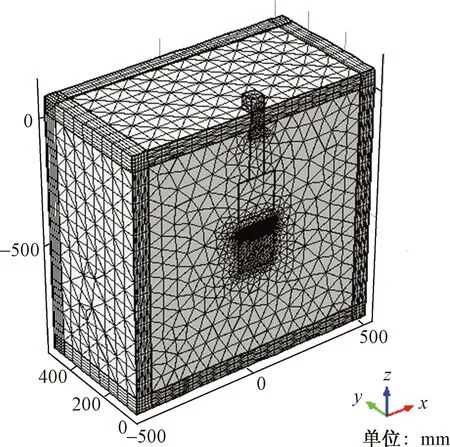
圖4 網格劃分圖Fig.4 Mesh map

在本模型的網格劃分過程中，首先進行PML層網格劃分，對PML層表面進行映射網格劃分，分成5段，對PML層實體進行掃掠網格劃分，分成5層，并將PML層表面的四邊形網格轉換成三角形網格；然后進行冰層和混凝土網格劃分，對冰層與混凝土接觸面進行自由三角形網格劃分控制冰層和混凝土的網格大小，在此基礎上，對冰層和混凝土實體進行自由四面體網格劃分；最后對剩余物理模型進行自由四面體網格劃分。

3 微波場特性研究

由于混凝土幾乎不具備磁損耗能力，故可以微波除冰模型的電場分布為例分析微波場特性。由于水對微波具有較強的吸收能力，而冰層幾乎不能吸收微波，因此冰層融化成水后對微波場的分布會產生一定的影響，以冰層融化前的電場為例分析微波場在豎直方向上的分布特點。圖5為微波除冰過程中電場的分布圖。

由圖5可知，電場的分布具有較強的對稱性，電場模形成的空間圖像就像一個緊挨一個的“圓柱體”排列在波導內，在圓柱體的中心部位電場模最大；微波進入輻射腔后，雖然電場模明顯變小，但是電場的均勻性明顯得到改善，同時其空間對稱性仍然存在；微波離開輻射腔后，僅在輻射腔和混凝土表面之間部分存在一定的電場，其他部分電場很快衰減；微波傳輸至冰層時，冰層界面并沒有引起電場模的突變，表明冰層幾乎不與微波發生作用。

圖6為電場隨波導中心軸的變化規律，橫坐標“距離”表示測試點離矩形波導端口的距離。

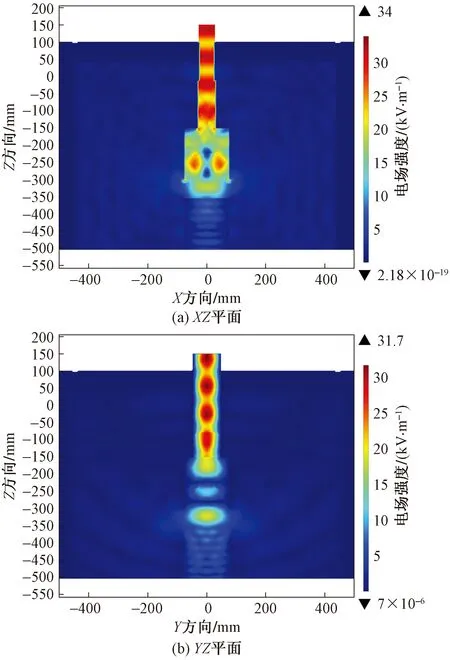
圖5 電場二維分布圖Fig.5 Electric field two-dimensional distribution map

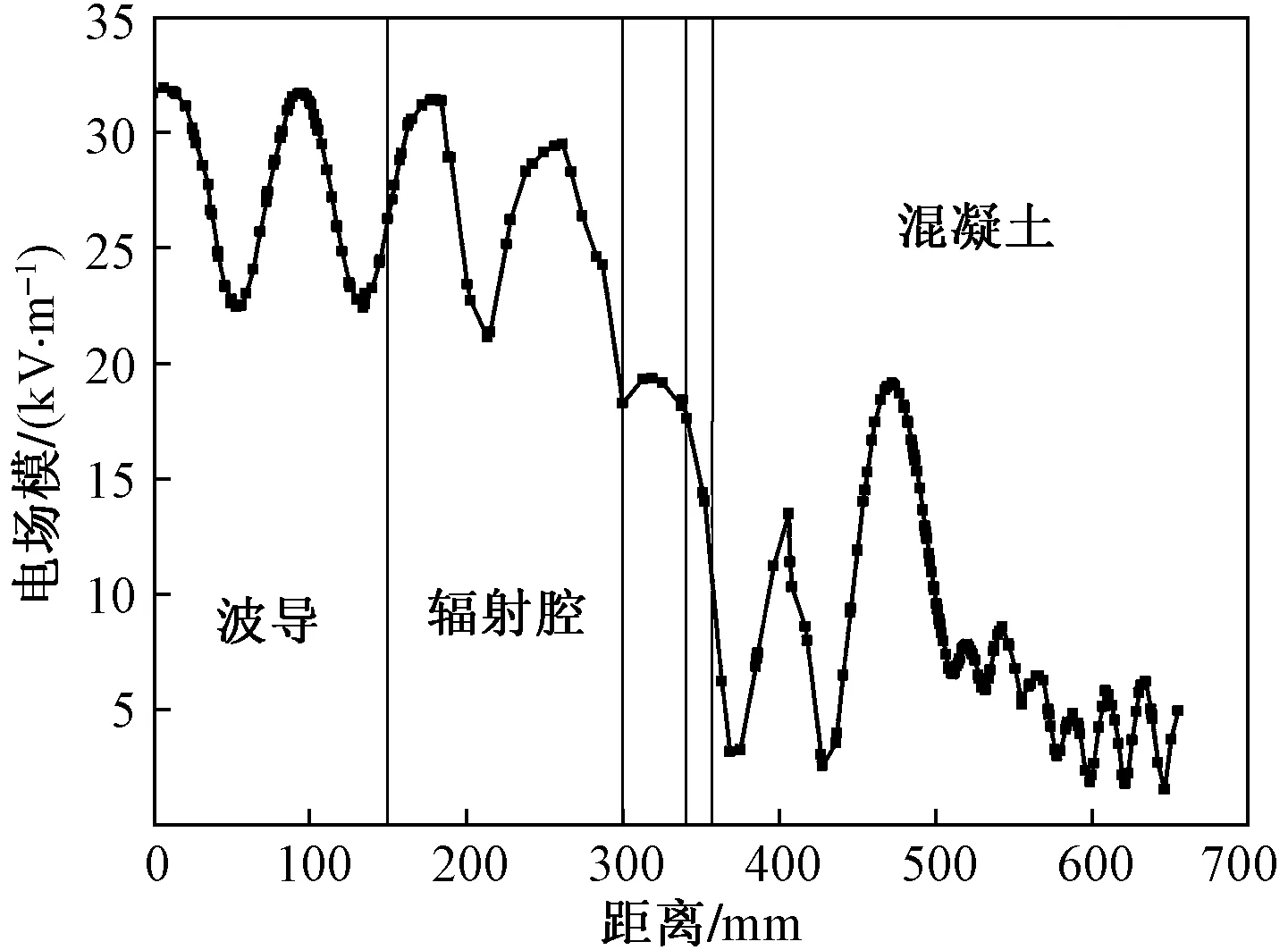
圖6 電場沿波導中心軸的變化規律Fig.6 The variation of the electric field along the central axis of the waveguide

由圖6可知，電場模在波導內呈正弦變化，最大值為31.9 kV/m，最小值為22.5 kV/m；進入輻射腔后，最大值降為29.5 kV/m，最小值降為18.3 kV/m；進入混凝土內部后，電場模逐漸變小。

圖7為電場在混凝土和冰層內部的二維分布圖。圖8為電場在混凝土表面以下10 mm處X軸和Y軸方向上的變化規律。

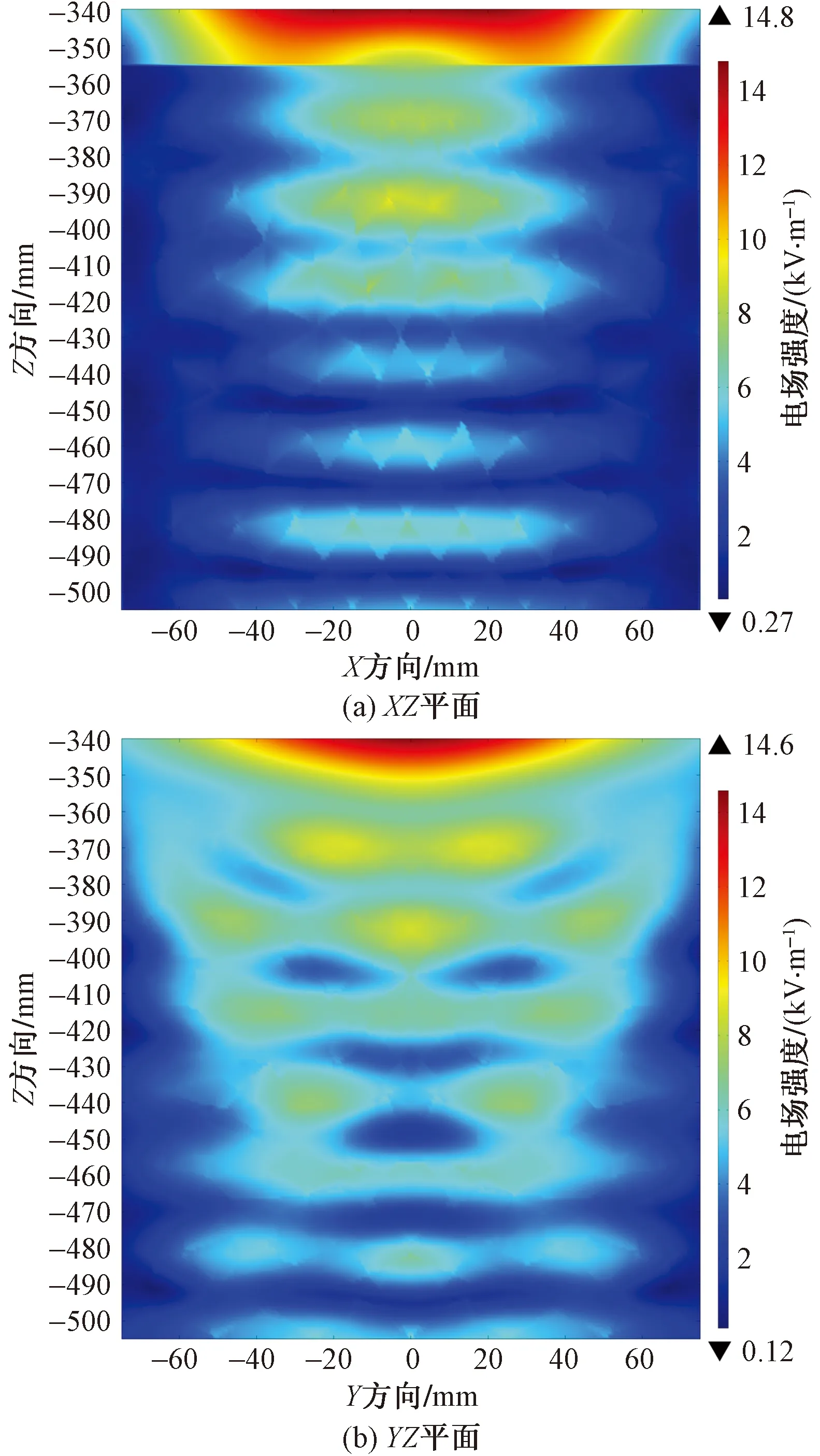
圖7 電場在混凝土內部的二維分布圖Fig.7 Two-dimensional distribution of electric field inside concrete

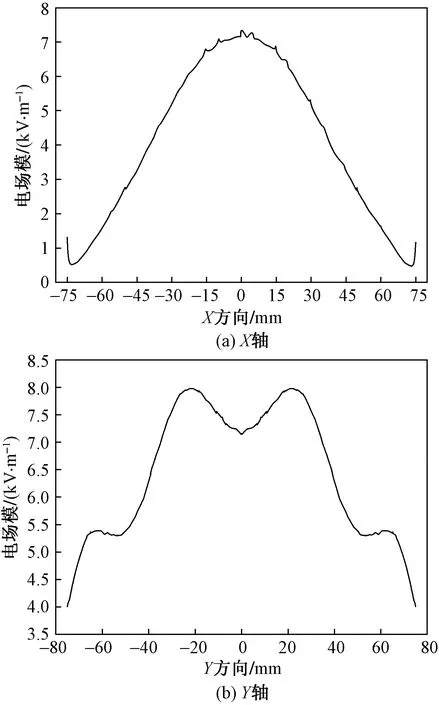
圖8 電場在混凝土表面下10 mm處兩個垂直方向的變化規律Fig.8 Variation of the electric field in two vertical directions at 10 mm below the concrete surface

由圖7和圖8可知，電場的透射情況與反射情況正好相反。以混凝土表面以下10 mm處的電場分布為例，在X軸方向上，電場模的分布形式為“Λ”形，電場模最大值在混凝土表面中心，其值為7.41 kV/m；電場最小值在混凝土表面邊緣，其值為0.56 kV/m。在Y軸方向上，電場模的分布形式為“M”形，電場模最大值在混凝土表面中心兩邊一定位置對稱分布，其值為8.26 kV/m；電場模最小值在混凝土表面邊緣，其值為4.06 kV/m；混凝土表面中心電場模為7.31 kV/m。同時可以看出，電場模沿Z軸方向是逐漸減小的，表面微波在混凝土中傳播時會產生損耗。

4 輻射端口高度研究

根據微波場特性分析可知，微波在豎向分布變化非常大，尤其是在空氣中衰減非常快，為此，有必要研究微波輻射端口高度對微波除冰效率的影響。將輻射腔端口到混凝土表面的豎向距離定義為輻射端口高度，很顯然，輻射端口高度不僅要滿足微波除冰工藝的需要，而且還要使微波效率達到最佳。采用仿真和試驗相結合的手段研究輻射腔端口高度與微波除冰效率的關系，輻射腔端口高度分別設定為20～70 mm，間隔5 mm，根據研究結果確定輻射腔端口最佳高度。

4.1 仿真研究

圖9為冰層融化前，不同輻射腔端口高度下混凝土表面微波發熱功率密度。

由圖9可知，微波發熱功率密度在混凝土表面的分布形狀與輻射腔端口高度有關。隨著輻射腔高度增大，微波發熱功率密度的分布形狀由“三點分布”向“橢圓分布”轉變。微波發熱功率密度是微波能轉化為熱量的效率，因而其分布形狀對微波加熱的均勻性十分重要，進而影響微波除冰的除凈率。在機場道面微波除冰過程中，由于微波源是掛載在除冰車底盤上，因此微波加熱區域是移動的。

圖10為微波加熱區域移動示意圖。

結合圖9中微波除冰系統加熱區域的分布，由圖10可知，對于“三點分布”的微波發熱功率密度，如果微波除冰系統沿X軸方向移動，由于加熱區域子在Y軸方向上覆蓋比例較少，則平行相鄰微波源之間的冰層難以被微波加熱區域覆蓋，冰層的除凈率不高；如果微波除冰系統沿Y軸方向移動，則三個相鄰加熱區域之間的冰層難以被微波加熱區域覆蓋，冰層的除凈率也不高。但是對于“橢圓分布”的微波發熱功率密度，由于微波加熱區域在Y軸方向上覆蓋比例較大，如果微波除冰系統沿X軸方向移動，則同排內相鄰加熱區域之間的冰層會被相鄰排的加熱區域所覆蓋，其他小部分冰層也能在周邊冰層的擠壓下脫離道面，因此，“橢圓分布”的微波發熱功率密度比“三點分布”的更加有利于機場道面微波除冰。

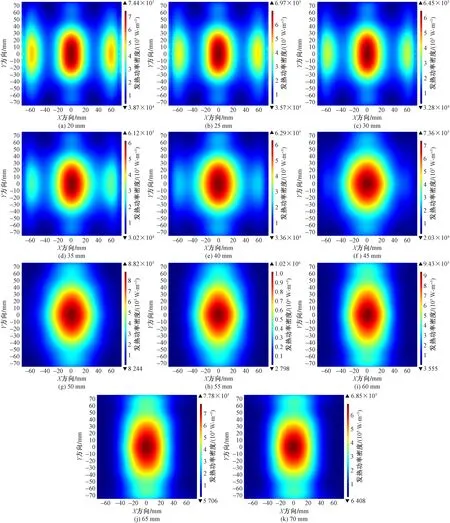
圖9 混凝土表面微波發熱功率密度Fig.9 Microwave heating power density of concrete surface

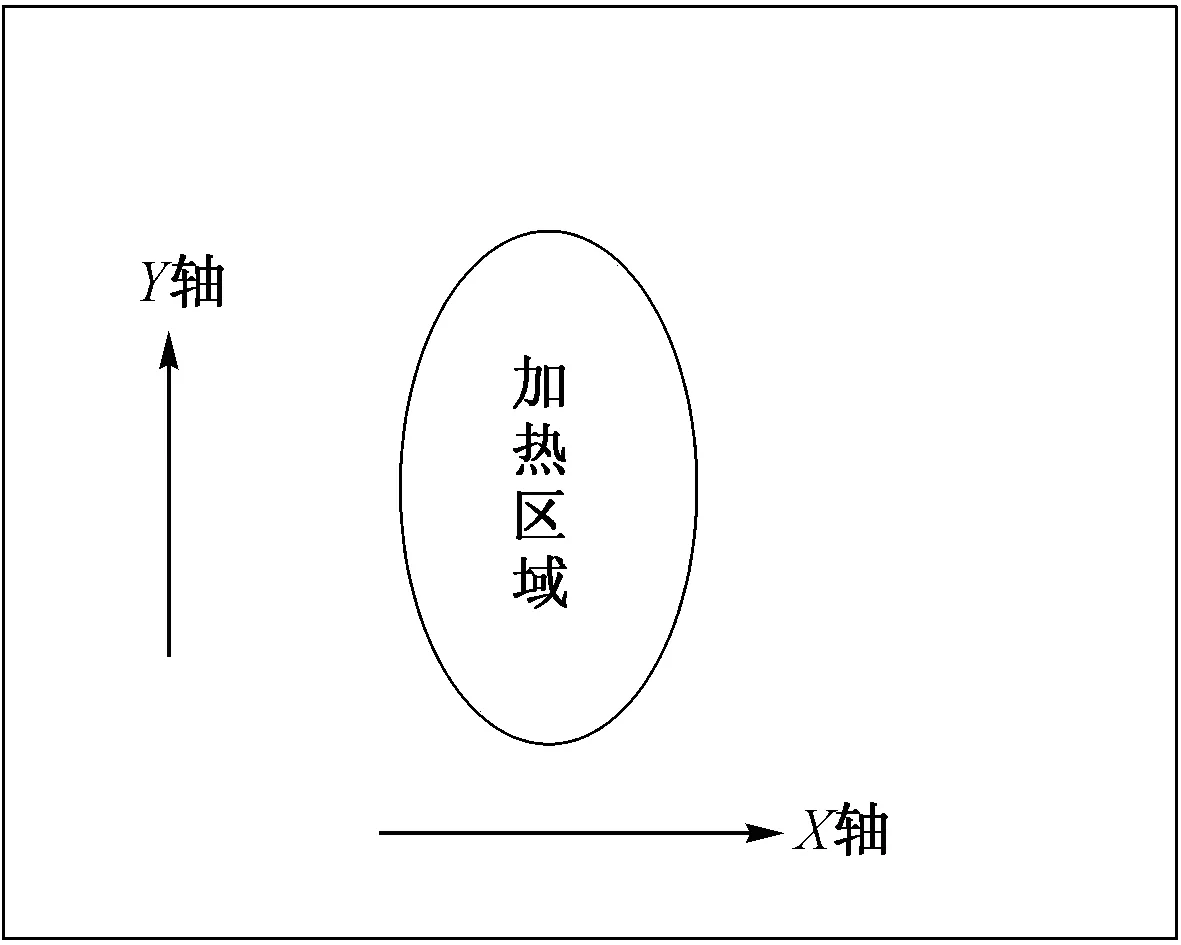
圖10 微波加熱區域移動示意圖Fig.10 Schematic diagram of microwave heating zone movement

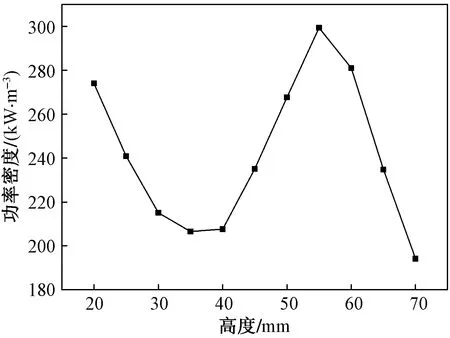
圖11 平均發熱功率密度隨端口高度的變化Fig.11 Variation of heating power density with port height

圖11為不同輻射腔端口高度下混凝土表面的平均微波發熱功率密度，圖12為不同輻射腔端口高度下混凝土表面中心溫度隨時間的變化規律。由圖11可知，輻射腔端口高度為55 mm時，混凝土表面的平均微波發熱功率密度達到最大，其值為299.30 kW/m。由圖12可知，輻射腔端口高度為55 mm時，混凝土表面升溫速度最快。綜上所述，結合機場道面微波除冰的實際需要，以及除冰過程中路面平整度的影響，輻射腔端口高度可設計為55 mm。

圖12 混凝土表面溫度隨時間的變化Fig.12 Variation of concrete surface temperature with time

4.2 試驗研究

為了驗證仿真模型的準確性，合理確定輻射腔端口高度的最佳值，進行了相應試驗。依據冰層的透波特性，在研究輻射腔端口高度與微波除冰性能關系時，可不考慮冰層的影響，采用無冰升溫試驗進行。試驗設備采用與微波除冰試驗相同的設備，如圖13所示，通過螺桿上圓形把手調節螺桿的伸出長度，從而控制輻射腔端口高度。

圖13 無冰升溫試驗設備Fig.13 Ice-free temperature test equipment

以混凝土表面中心的溫度變化規律為指標，研究不同輻射腔端口高度下微波在混凝土表面的發熱效率。通過粘貼在混凝土表面中心的光纖型號為YT-PL的光纖溫度傳感器記錄混凝土表面的溫度變化。初始溫度10 ℃左右，不同輻射腔端口高度下混凝土表面的溫度變化規律如圖14所示。

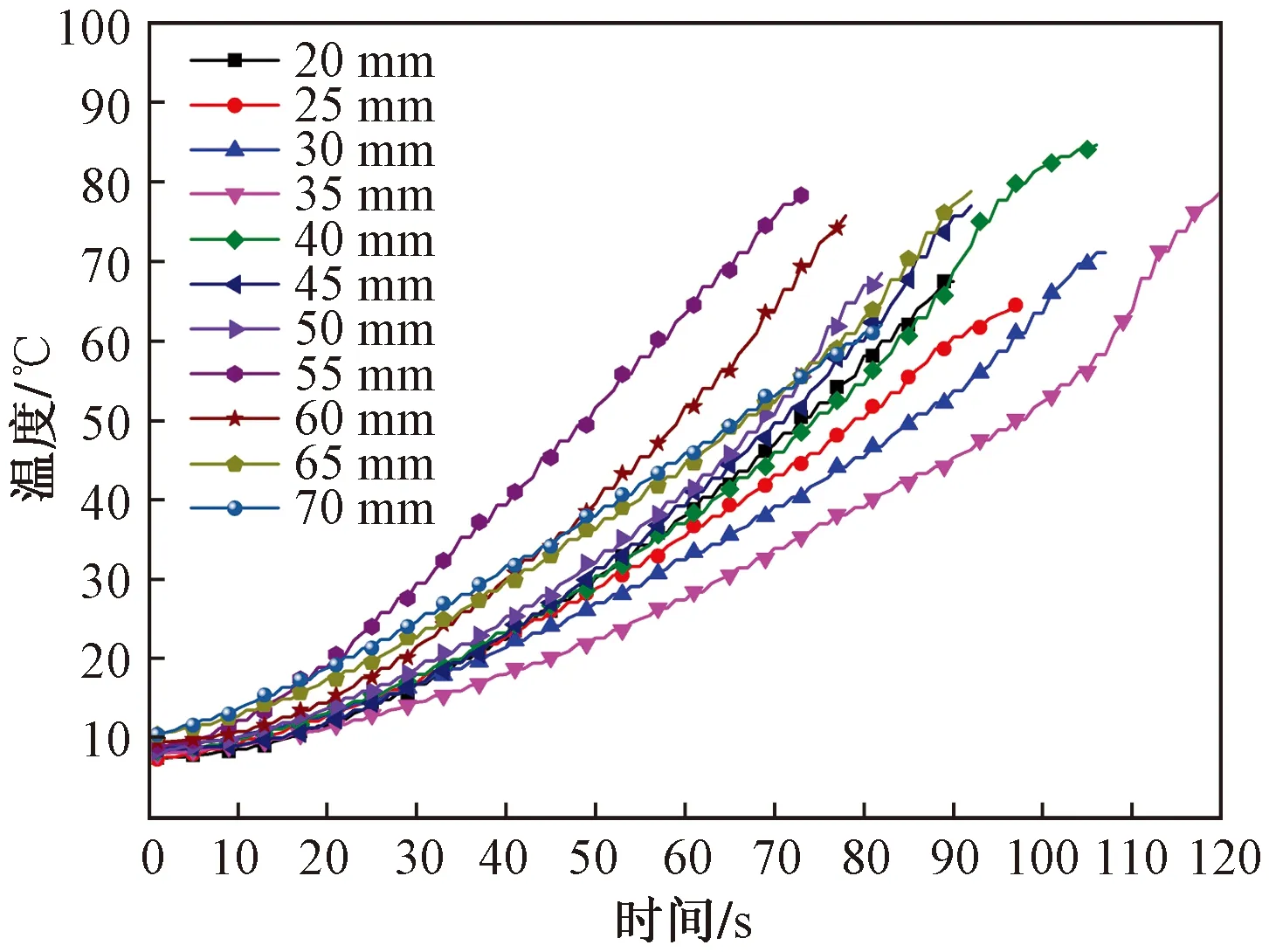
圖14 混凝土表面溫度隨時間的變化Fig.14 Variation of concrete surface temperature with time

對圖14中不同升溫曲線進行擬合，得到擬合參數，其結果如表2所示。

由圖14和表2可知，輻射腔端口高度從20 mm變化到70 mm，混凝土表面升溫速率的變化趨勢為先變小、后增大、最后再減小，當高度為45 mm和50 mm，混凝土表面升溫速率有一點異常，這是實驗誤差引起的。當高度為55 mm時，混凝土表面升溫速率達到最大值，其值為1.031 ℃/s。很顯然，仿真研究與實驗研究得到的結果是一致的，表明所建立的機場道面微波除冰模型具有較高的準確性。

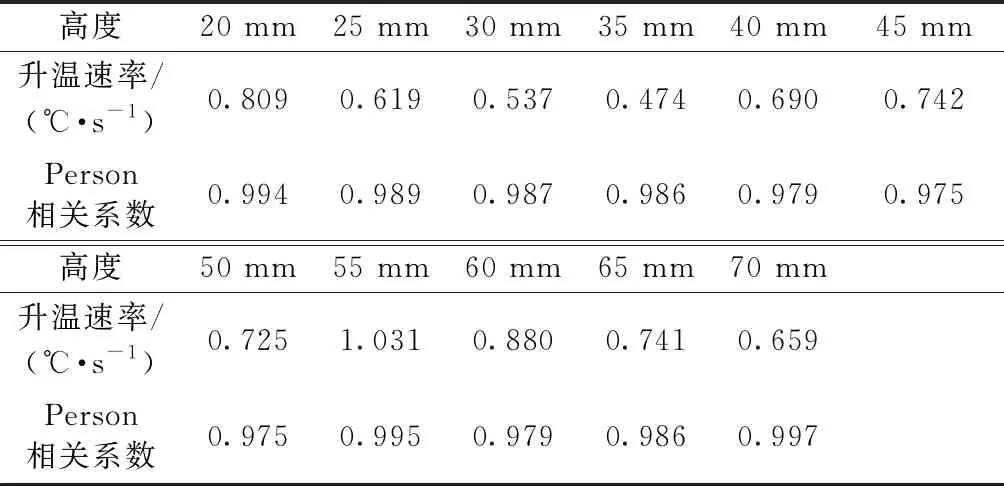
表2 不同輻射腔端口高度下混凝土表面升溫曲線的擬合參數Table 2 Fitting parameters of concrete surface heating curve under different radiant cavity port heights

綜上所述，微波除冰過程中最佳輻射端口高度可設計為55 mm。

5 結論

微波輻射端口高度是影響其應用和微波除冰效率的關鍵因素，分析了微波除冰技術的除冰機理，以COMSOL Multiphysics軟件為平臺建立了微波除冰仿真模型，在分析微波場特性的基礎上，采用仿真與試驗相結合的手段研究輻射端口高度對混凝土道面微波除冰性能的影響，主要結論如下。

(1)分析了微波除冰機理，冰層具有透波性質，微波能夠透過冰層與混凝土道面相互作用，將微波能量轉化為熱量，利用該熱量融化冰層與道面的黏結層，使冰層與道面發生脫離。

(2)以微波損耗能量方程和非穩態導熱方程作為理論基礎，選擇COMSOL Multiphysics軟件為平臺，通過模型建立、參數設定和網格劃分建立了微波除冰仿真模型。

(3)分析了微波在豎直方向上的分布特點，微波在波導中呈正弦變化，進入輻射腔后略有降低，在空氣中衰減很快，進入混凝土后逐漸降低。

(4)仿真結果與實驗結果較為接近，表明COMSOL Multiphysics建立的微波除冰仿真模型具有較高的準確性。

(5)研究結果表明，微波除冰過程中最佳輻射端口高度可設計為55 mm。

隨著各個國家對綠色能源的開發利用，微波除冰技術作為一種綠色環保的除冰方法，在未來將會有更加廣闊的應用前景，研究結論可為其應用提供技術指導。