懸索面內(nèi)1/3次諧波共振瞬時(shí)相頻特性

陳 皓， 孫測(cè)世

(重慶交通大學(xué)土木工程學(xué)院， 重慶 400074)

懸垂纜索在高壓輸電及橋梁中具有廣泛的應(yīng)用，但其作為高強(qiáng)度、低阻尼的柔性結(jié)構(gòu)，因初始垂度引起的非線性使其力學(xué)特性變得復(fù)雜[1]，易在風(fēng)雪等外荷載作用下產(chǎn)生各種次諧波共振，常常引起結(jié)構(gòu)的破壞[2-3]，例如輸電線舞動(dòng)嚴(yán)重時(shí)會(huì)導(dǎo)致相鄰輸電線碰撞而產(chǎn)生閃絡(luò)，甚至使輸電系統(tǒng)癱瘓[4-5]，引發(fā)廣泛關(guān)注。

相鄰懸索碰撞需要同時(shí)滿足大幅振動(dòng)及振動(dòng)反相，目前各國(guó)學(xué)者已對(duì)懸索的次諧波共振機(jī)理開展了大量的研究，但其主要針對(duì)不同參數(shù)及耦合機(jī)理下響應(yīng)的幅值[6]或某一組參數(shù)下響應(yīng)相位[7-8]，而針對(duì)不同參數(shù)下懸索響應(yīng)相位的研究較少。已有研究結(jié)果表明，懸索響應(yīng)與激勵(lì)相位差與激勵(lì)頻率密切相關(guān)[9]。與之類似，文獻(xiàn)[10]進(jìn)行了斜拉橋全橋模型試驗(yàn)，在主梁跨中施加豎向簡(jiǎn)諧激勵(lì)，觀測(cè)到兩根相鄰斜拉索發(fā)生異步的大幅振動(dòng)，通過(guò)掃頻試驗(yàn)得到兩者穩(wěn)態(tài)振動(dòng)的相位差隨激勵(lì)頻率的變化曲線。對(duì)于多模態(tài)而言，Hu等[11]的研究表明斜拉索不同模態(tài)間同樣存在相位差，且隨激勵(lì)頻率變化而改變。而結(jié)構(gòu)參數(shù)差異同樣會(huì)對(duì)其相頻特性產(chǎn)生較大影響，趙珧冰等[12]、黃超輝等[13]研究發(fā)現(xiàn)溫度變化會(huì)引起系統(tǒng)非線性共振響應(yīng)特性發(fā)生定性和定量的變化，對(duì)共振響應(yīng)區(qū)間及相位產(chǎn)生直接影響。此外，開展對(duì)懸索響應(yīng)相位的研究是后續(xù)開展輔助索減振研究的基礎(chǔ)之一，研究表明，當(dāng)相鄰索之間出現(xiàn)反相振動(dòng)時(shí)，輔助索減振效果良好，而同相振動(dòng)時(shí)其作用很小[14]。

綜上，激勵(lì)頻率及參數(shù)差異會(huì)對(duì)懸索響應(yīng)相位產(chǎn)生較大影響，而垂跨比對(duì)于懸索而言為非常重要的結(jié)構(gòu)參數(shù)。因此，現(xiàn)研究不同垂跨比下懸索發(fā)生面內(nèi)1/3次諧波共振的響應(yīng)與激勵(lì)的瞬時(shí)相位差的隨垂跨比及激勵(lì)頻率的變化規(guī)律，并著重分析高階項(xiàng)及漂移項(xiàng)成分的影響。

1 力學(xué)模型

建立圖1所示懸索非線性動(dòng)力學(xué)模型，為簡(jiǎn)化計(jì)算，做出以下假設(shè)：①懸索的靜力平衡曲線為二次拋物線；②忽略懸索的抗彎、剪切及抗扭剛度；③懸索在振動(dòng)過(guò)程中處于彈性變形范圍。懸索振動(dòng)采用局部坐標(biāo)O-xyz來(lái)描述：坐標(biāo)原點(diǎn)O，x為懸索弦線方向，y為索面內(nèi)垂直弦線的方向，x、y方向?qū)?yīng)位移分別用u、w表示，l為索長(zhǎng)。

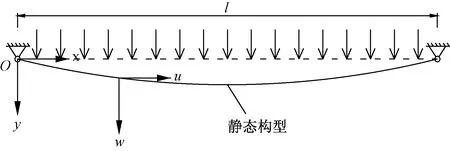
圖1 分布面內(nèi)激勵(lì)下懸索振動(dòng)簡(jiǎn)化模型Fig.1 Simplified model of suspension cable vibration under in-plane excitation

1.1 控制方程

考慮拉索初始垂度與幾何非線性，懸索兩端鉸接。通過(guò)利用Hamilton原理得到分布面內(nèi)激勵(lì)下懸索面內(nèi)非線性振動(dòng)力學(xué)方程[15]為

(1)

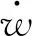
y=4fx(1-x)

(2)

式(2)中：f為垂跨比。

設(shè)拉索以擬靜態(tài)方式進(jìn)行軸向振動(dòng)，略去高階無(wú)窮小量，拉索無(wú)量綱控制方程為

(3)

采用的無(wú)量綱變換有

為了方便書寫，省去“*”號(hào)。

1.2 離散化模型

在分布外激勵(lì)作用下，懸索振動(dòng)位移被認(rèn)為是由純振動(dòng)產(chǎn)生，因此令

(4)

式(4)中：φn為模態(tài)函數(shù)；qn為廣義坐標(biāo)函數(shù)。

正對(duì)稱模態(tài)函數(shù)為

(5)

式(5)中：ωn為懸索n階固有頻率。

(6)

反對(duì)稱模態(tài)函數(shù)為

(7)

利用Galerkin方法得到

(8)

1.3 攝動(dòng)分析

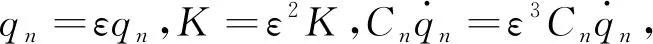
qn(T0,T1,T2)=q0(T0,T1,T2)+εq1(T0,T1,T2)+ε2q2(T0,T1,T2)+…

(9)

式(9)中:Tn=εnt(n=0,1,2,…)，將式(9)代入式(8)，并按照ε的冪次進(jìn)行整理，可以得到下列方程。

(10)

(11)

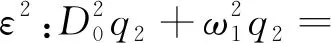
(12)

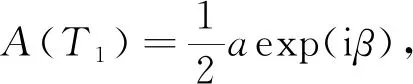
(13)

(14)

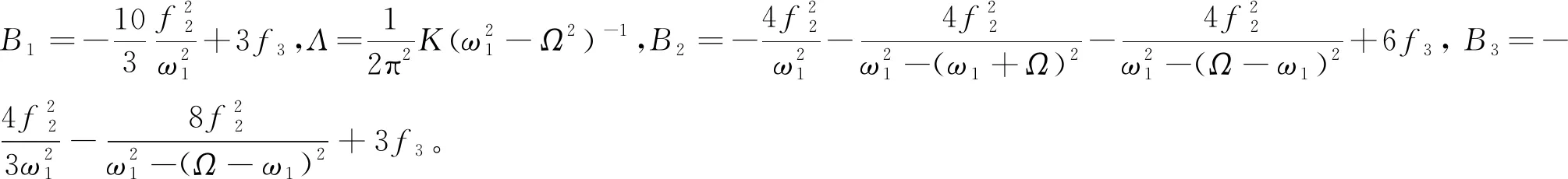
設(shè)γ=σT0-3β，令a′=γ′=0，此時(shí)幅頻響應(yīng)方程的表達(dá)式為

(15)

面內(nèi)運(yùn)動(dòng)方程的二階近似解為

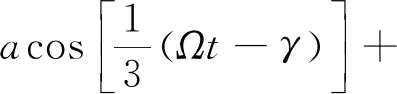
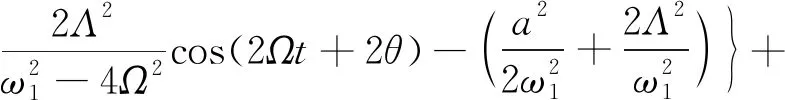
(16)

式(13)中：O(ε2)為高階無(wú)窮小量。

由式(16)可知，近似解由線性項(xiàng)、高階項(xiàng)和漂移項(xiàng)三部分組成，由于高階項(xiàng)及漂移項(xiàng)的影響，其瞬時(shí)相頻特性變得復(fù)雜，為便于后文分析，定義為

(17)

2 數(shù)值算例

利用MATLAB進(jìn)行數(shù)值計(jì)算，得到不同垂跨比下懸索瞬時(shí)相頻特性的變化規(guī)律。算例分析中懸索各項(xiàng)物理參數(shù)如表1所示，另外無(wú)量綱化后的激勵(lì)幅值和阻尼系數(shù)分別為0.02和0.005。

結(jié)合懸索參數(shù)，根據(jù)式(12)得到了懸索垂跨比為0.006及0.01時(shí)的幅頻響應(yīng)曲線，并將結(jié)果與文獻(xiàn)[16]進(jìn)行了對(duì)比，結(jié)果如圖2所示。可以看出，兩者結(jié)果大體吻合，但略微有一定差異，當(dāng)垂跨比為0.006時(shí)，兩者的最大誤差為6.0%，而當(dāng)垂跨比為0.010時(shí)，兩者的最大誤差為1.4%。

表1 懸索參數(shù)[16]Table 1 Suspended cable parameters[16]

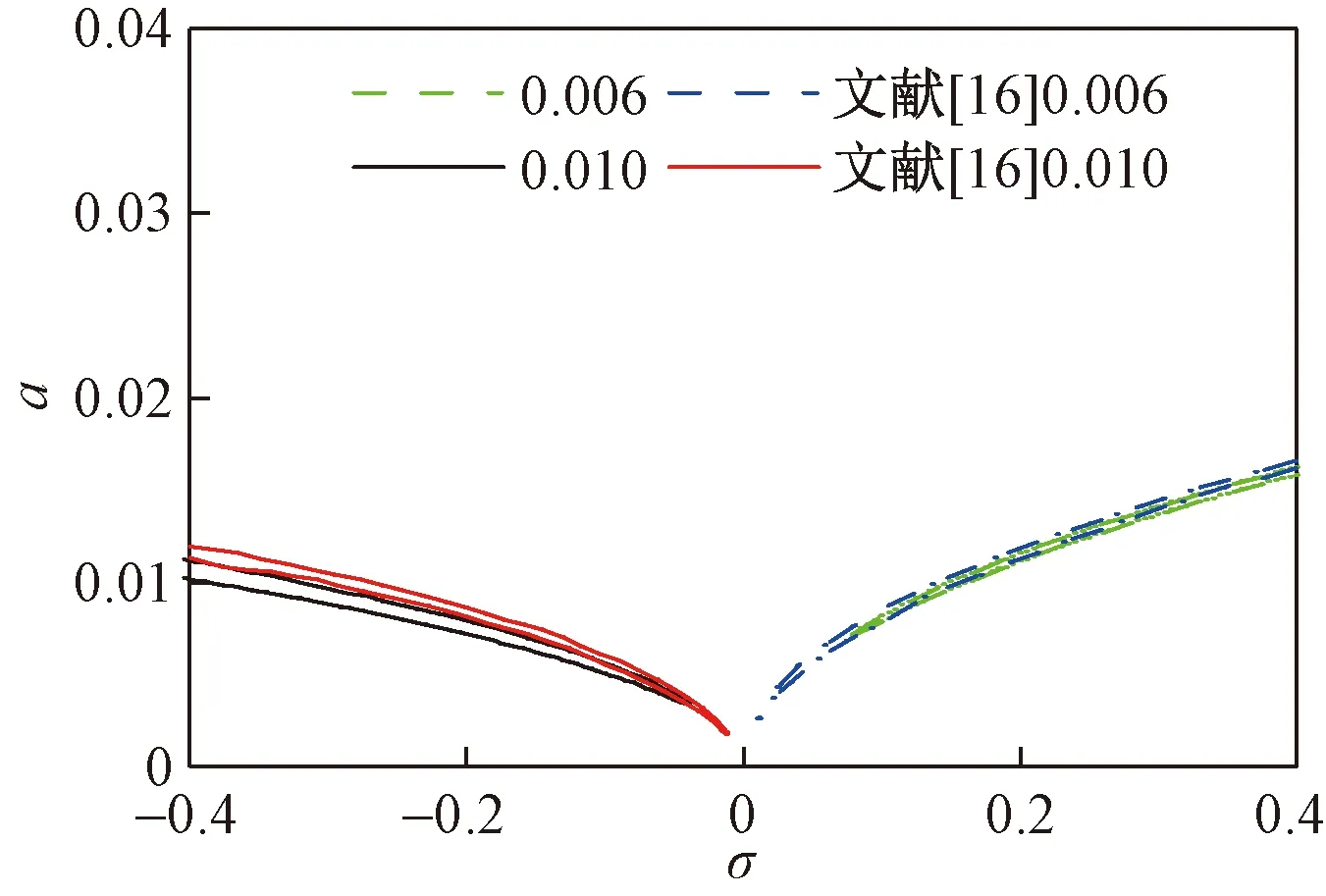
圖2 幅頻響應(yīng)曲線Fig.2 Amplitude-frequency response

2.1 不同垂跨比下響應(yīng)與激勵(lì)的瞬時(shí)相位差

為研究垂跨比對(duì)懸索瞬時(shí)相頻特性的影響，首先研究不同垂跨比懸索在單個(gè)激勵(lì)頻率下的響應(yīng)。文獻(xiàn)[18]表明垂跨比的大小在非線性動(dòng)力學(xué)分析特性時(shí)非常重要，根據(jù)其選擇4種垂跨比分別為0.008 5、0.010、0.015、0.02，對(duì)應(yīng)懸索固有頻率分別為1.155、1.242、1.669、2.211，為滿足1/3亞諧波共振，確定激勵(lì)頻率的方式采用固定的調(diào)諧參數(shù)-0.5。對(duì)于次諧波共振而言，每種垂跨比下的懸索均會(huì)對(duì)應(yīng)兩個(gè)非平凡解，但重點(diǎn)不在于分岔問(wèn)題，因此不區(qū)分解的穩(wěn)定，僅取其中一個(gè)解進(jìn)行分析。

圖3為4種垂跨比下的響應(yīng)時(shí)程曲線，因不同垂跨比的懸索對(duì)應(yīng)的激勵(lì)頻率不同，導(dǎo)致不同懸索之間的響應(yīng)幅值及周期相差較大，但很明顯可以看出，當(dāng)f=0.008 5和f=0.01時(shí)，其響應(yīng)的時(shí)程曲線呈現(xiàn)“上寬下窄”，且整個(gè)曲線向上漂移，而垂跨比為0.015和0.02時(shí)的響應(yīng)時(shí)程曲線較為接近正弦波的形式。

對(duì)懸索響應(yīng)及激勵(lì)的時(shí)程曲線分別進(jìn)行Hilbert變換，得到響應(yīng)與激勵(lì)的瞬時(shí)相位差時(shí)程曲線，如圖4所示。

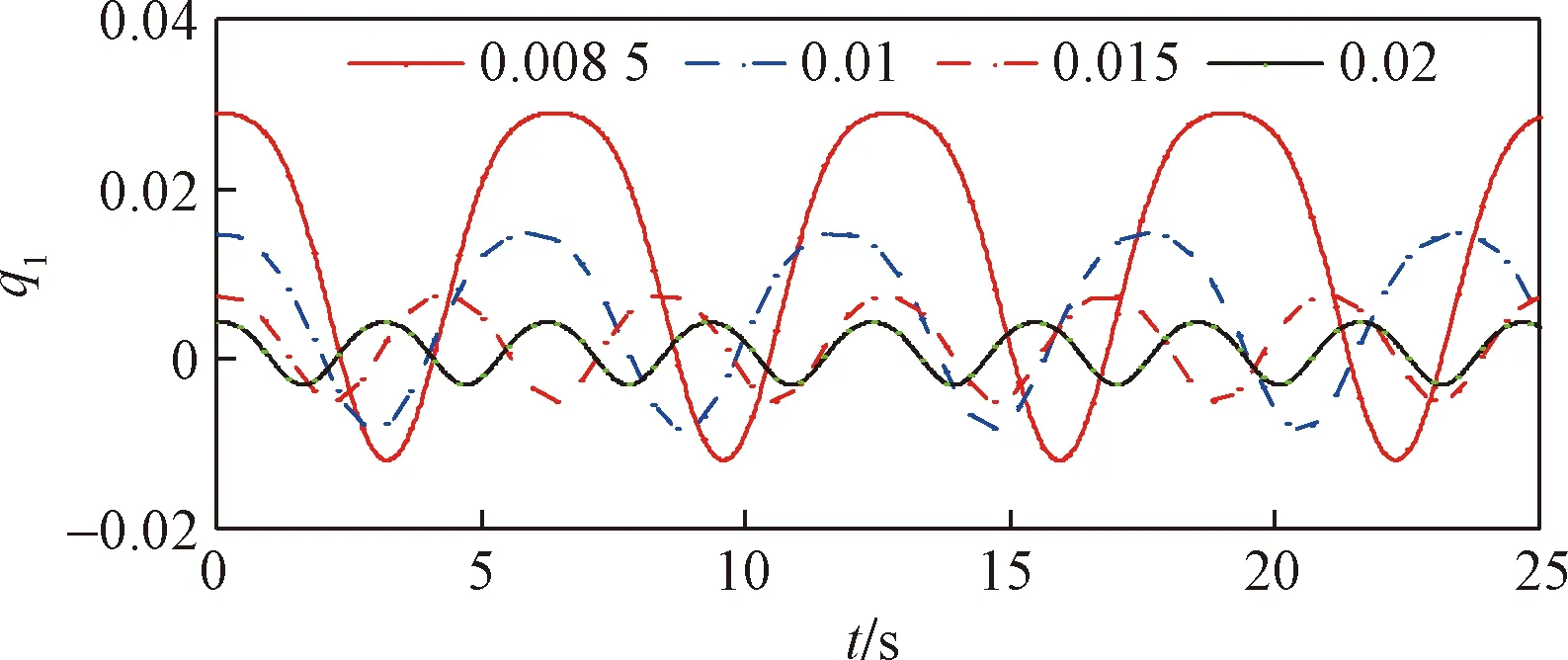
圖3 響應(yīng)時(shí)程曲線Fig.3 Response time history

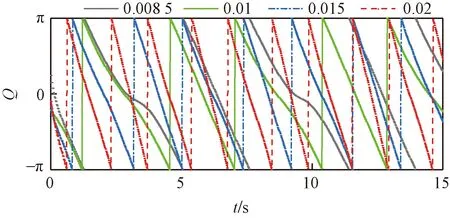
圖4 響應(yīng)與激勵(lì)的瞬時(shí)相位差時(shí)程曲線(σ=-0.5)Fig.4 Time history of transient phase difference between response and excitation (σ=-0.5)

各懸索響應(yīng)與激勵(lì)瞬時(shí)相位差值呈周期性變化，該周期等于與激勵(lì)周期一致。因懸索與激勵(lì)滿足1/3亞諧波共振，兩者在同一個(gè)響應(yīng)周期內(nèi)會(huì)出現(xiàn)兩次反相的狀態(tài)，即該差值在一個(gè)周期內(nèi)會(huì)出現(xiàn)2次接近-π的情況。對(duì)比各懸索發(fā)現(xiàn)，當(dāng)f=0.008 5和f=0.01時(shí)，一個(gè)振動(dòng)周期內(nèi)部明顯分為兩個(gè)時(shí)長(zhǎng)不等的遞減區(qū)間，且當(dāng)f=0.008 5時(shí)，瞬時(shí)相位差在周期內(nèi)的變化速率會(huì)由快變慢再變快，而其余3種垂跨比下瞬時(shí)相位差均迅速降低且變化速率無(wú)明顯變化，結(jié)合圖3和式(13)分析，應(yīng)是響應(yīng)中高階項(xiàng)和漂移項(xiàng)的影響。

2.2 高階項(xiàng)和漂移項(xiàng)對(duì)于響應(yīng)瞬時(shí)相位的影響

為考慮高階項(xiàng)和漂移項(xiàng)對(duì)響應(yīng)瞬時(shí)相位的響應(yīng)，分別對(duì)q1和Q進(jìn)行Hilbert變換，并定義無(wú)量綱參數(shù)如下。

(18)

式(18)中：ΔPh為q1和Q的瞬時(shí)相位之差，ΔPhmax為ΔPh幅值最大值，對(duì)兩者無(wú)量綱化得到Ph及Phmax。由于q1為系統(tǒng)的全部響應(yīng)，而Q僅是響應(yīng)的線性項(xiàng)，因此ΔPh實(shí)際上反映高階項(xiàng)及漂移項(xiàng)對(duì)瞬時(shí)相位的貢獻(xiàn)；ΔPhmax為ΔPh的幅值最大值。

考慮到不同垂跨比下懸索響應(yīng)周期不一致，為更直觀比較f改變對(duì)Ph的影響，通過(guò)周期變換(縱坐標(biāo)不變)，消除因懸索固有頻率差異而導(dǎo)致的瞬時(shí)相位差，將各懸索的Ph時(shí)程變化曲線都統(tǒng)一為f=0.008 5的周期，如圖5所示。

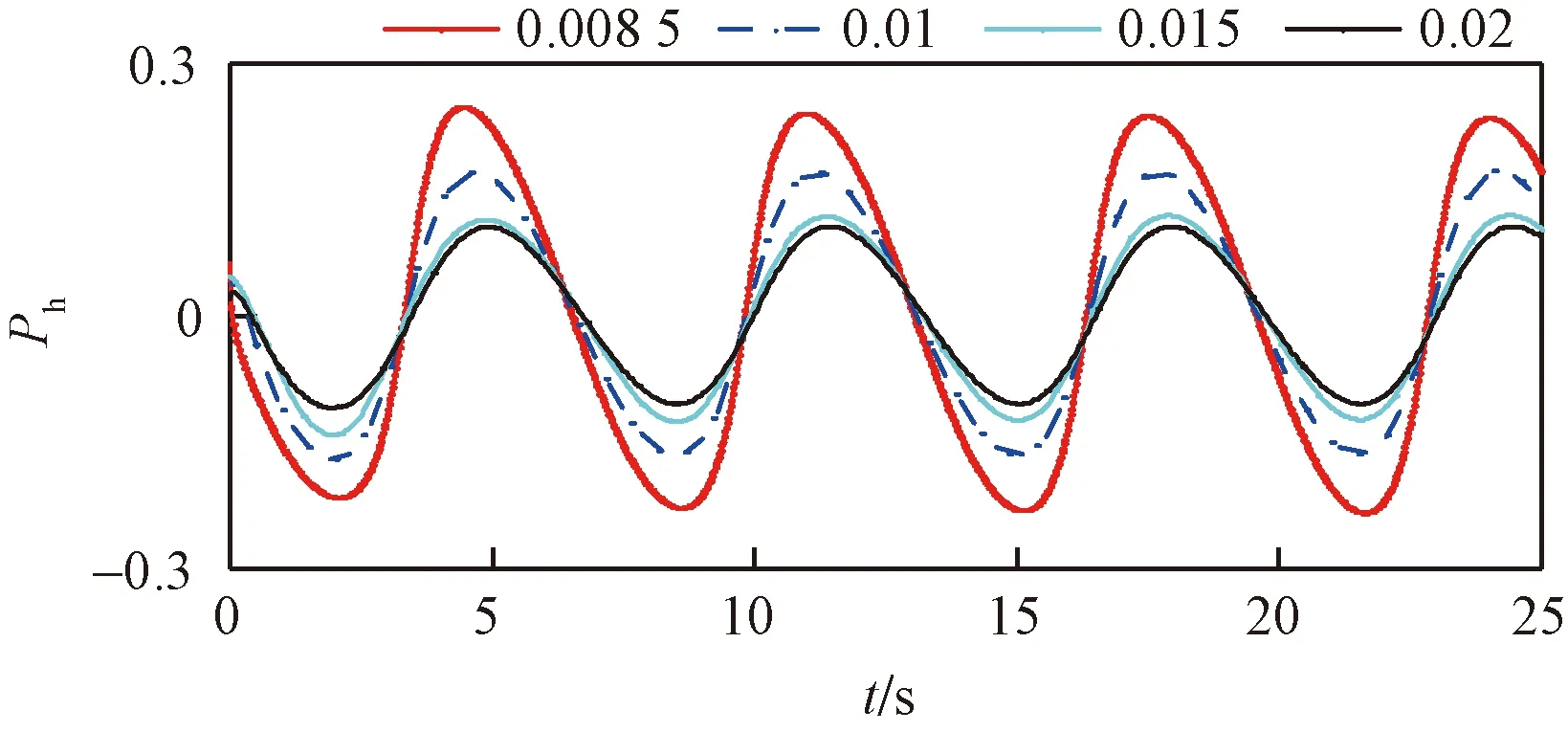
圖5 周期變換過(guò)后的瞬時(shí)相位差時(shí)程曲線(σ=-0.5)Fig.5 Time history of transient phase difference after periodic transformation (σ=-0.5)

對(duì)比各懸索，發(fā)現(xiàn)Phmax隨著f增大逐漸減小，但f從0.008 5變?yōu)?.01時(shí)，Phmax的變化值顯然比從0.015變至0.02大，說(shuō)明高階項(xiàng)和漂移項(xiàng)對(duì)響應(yīng)瞬時(shí)相位的影響大小與懸索參數(shù)取值范圍有關(guān)。同時(shí)兩者不僅對(duì)Phmax的數(shù)值大小有影響，當(dāng)f為0.008 5和0.010的時(shí)候，它還使得Phmax出現(xiàn)的時(shí)機(jī)提前，對(duì)于同一個(gè)周期而言，從Phmax減少到-Phmax需要的時(shí)間長(zhǎng)于從-Phmax增加到Phmax的時(shí)間，而當(dāng)f為0.015和0.020時(shí)，該現(xiàn)象并不明顯，因此圖4中響應(yīng)與激勵(lì)的瞬時(shí)相位差在同一個(gè)周期內(nèi)會(huì)出現(xiàn)兩個(gè)時(shí)長(zhǎng)不等遞減區(qū)間的原因?yàn)楦唠A項(xiàng)和漂移項(xiàng)的影響。

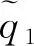
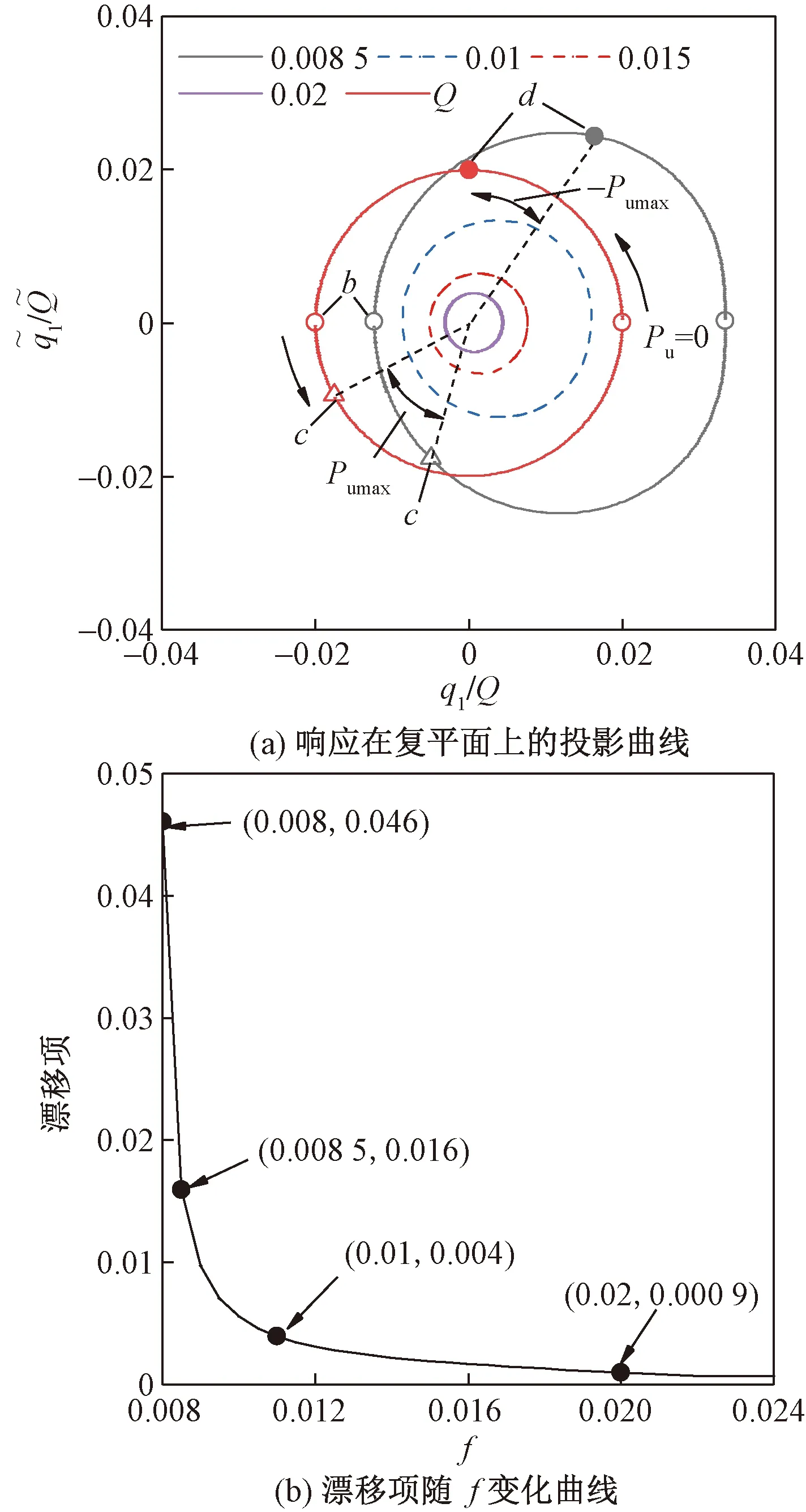
圖6 高階項(xiàng)和漂移項(xiàng)對(duì)響應(yīng)瞬時(shí)相位的影響(σ=-0.5)Fig.6 Influence of higher-order term and drift term on transient phase of response (σ=-0.5)

整體而言，對(duì)比不同垂跨比懸索響應(yīng)及線性項(xiàng)的復(fù)平面投影曲線發(fā)現(xiàn)，兩者有很大不同，因漂移項(xiàng)的影響，各響應(yīng)投影曲線明顯整體往一二象限平移，且隨著f的減小平移的趨勢(shì)變得越大。具體而言，當(dāng)f=0.008 5時(shí)，其響應(yīng)投影曲線并非圓形，應(yīng)是高階項(xiàng)對(duì)其的影響，但不明顯。在起點(diǎn)b與1/2周期處Ph為0，在c點(diǎn)時(shí)Ph有最大值Phmax，在d點(diǎn)Ph有最小值-Phmax，且c點(diǎn)與d點(diǎn)之間的時(shí)間間隔明顯長(zhǎng)于d點(diǎn)與b點(diǎn)之間，與圖2中響應(yīng)時(shí)程曲線“上寬下窄”特征相吻合，表明當(dāng)垂跨比較小時(shí)，高階項(xiàng)會(huì)引起Phmax出現(xiàn)的時(shí)機(jī)提前，導(dǎo)致響應(yīng)與激勵(lì)的瞬時(shí)相位差在同一個(gè)周期內(nèi)會(huì)出現(xiàn)兩個(gè)時(shí)長(zhǎng)不等遞減區(qū)間。由此，表明漂移項(xiàng)對(duì)Phmax數(shù)值大小起主導(dǎo)作用，而高階項(xiàng)的影響則較小。

繪制漂移項(xiàng)隨f變化曲線，如圖6(b) 所示。由圖6(b)可知，當(dāng)f為0.008時(shí)，漂移項(xiàng)有最大值0.046，f從0.008 5增長(zhǎng)到0.010，漂移項(xiàng)迅速減小到0.004，而在0.010到0.02范圍內(nèi)，漂移項(xiàng)的數(shù)值緩慢減小。結(jié)合圖6(a)及圖6(b)分析，表明各懸索垂跨比的不同主要通過(guò)改變其漂移項(xiàng)的大小來(lái)影響其瞬時(shí)相位。

2.3 參數(shù)分析

為進(jìn)一步研究Phmax、垂跨比及調(diào)諧參數(shù)三者之間的關(guān)系，f取值[0.008,0.024]，變化步長(zhǎng)為0.001，調(diào)諧參數(shù)取值[-0.6,0]，變化步長(zhǎng)為0.02，繪制f-σ-Phmax曲面圖在f-σ平面、f-Phmax平面及σ-Phmax平面的投影曲線如圖7所示。

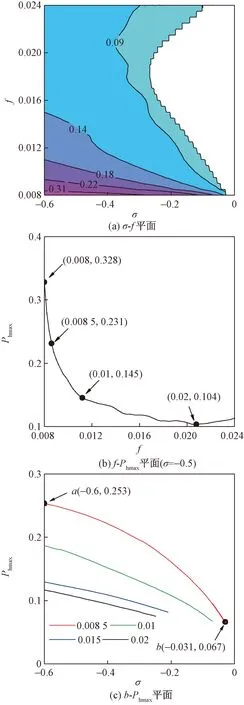
圖7 f-σ-Phmax曲面Fig.7 f-σ-Phmax surface

圖7(a)為f-σ等高線圖。當(dāng)垂跨比為[0.008,0.012]時(shí)等高線更密集，且等高線數(shù)值的變化更大，說(shuō)明該范圍內(nèi)Phmax對(duì)垂跨比及激勵(lì)頻率變化更加敏感。

圖7(b)為σ=-0.5時(shí)f-Phmax平面投影曲線。表明懸索f變化對(duì)Phmax影響較大，Phmax在f=0.008時(shí)有最大值0.328，當(dāng)0.008

圖7(c)為4種垂跨比下懸索的σ-Phmax曲線圖，可以發(fā)現(xiàn)調(diào)諧參數(shù)的改變同樣會(huì)對(duì)Phmax產(chǎn)生較大的影響。Phmax整體均隨著σ增大而減小，即響應(yīng)中高階項(xiàng)和漂移項(xiàng)成分對(duì)響應(yīng)瞬時(shí)相位的影響隨著調(diào)諧參數(shù)的增大而逐漸減小。對(duì)比各懸索發(fā)現(xiàn)，垂跨比越小，調(diào)諧參數(shù)對(duì)Phmax的影響越明顯，當(dāng)f=0.008 5時(shí)，Phmax最大值能達(dá)到0.253，同時(shí)隨著σ的變化，Phmax減小的速率逐漸變快，而其余3個(gè)垂跨比下懸索的Phmax與σ基本呈負(fù)相關(guān)。因此，對(duì)于垂跨比較小的懸索而言，高階項(xiàng)和漂移項(xiàng)對(duì)響應(yīng)相位的影響隨調(diào)諧參數(shù)的變化會(huì)變得復(fù)雜，其變化速率逐漸加快，而對(duì)于垂跨比較大的懸索，調(diào)諧參數(shù)與其基本呈負(fù)相關(guān)。

3 結(jié)論

(1)高階項(xiàng)及漂移項(xiàng)成分對(duì)其瞬時(shí)相位具有較大影響，若不計(jì)兩者的影響瞬時(shí)相位差的誤差，甚至能達(dá)到0.328π，其中，漂移項(xiàng)起主導(dǎo)作用。

(2)響應(yīng)與線性項(xiàng)的最大相位差與垂跨比成反比，當(dāng)垂跨比較小時(shí)，垂跨比的微小改變會(huì)引起該相位差最大值的巨大變化。

(3)響應(yīng)與線性項(xiàng)的最大相位差整體隨調(diào)諧參數(shù)增大而逐漸減小，且對(duì)于垂跨比較小的懸索而言，調(diào)諧參數(shù)的變化使該相位差變化速率逐漸加快。