含預制裂紋的大理巖細觀損傷試驗研究

吳俊宇，謝東誼，朱珍德，謝興華

(1. 河海大學 巖土力學與堤壩工程教育部重點實驗室，江蘇 南京 210098； 2. 山東省沂源縣自然資源局，山東 淄博 256100；3. 南京水利科學研究院，江蘇 南京 210029)

隨著礦產資源勘探開發、交通工程、市政建設和地下空間開發的需要，巖石工程的規模越來越大，所涉及的巖石力學問題也越來越復雜。巖石變形、破壞的預測是巖石工程分析和設計的重點[1-3]。為了探究巖石的變形、破壞規律，國內外學者進行了大量研究[4-8]。Kassner等[9]認為，更深入地研究巖石的破壞機制，必須建立多尺度的力學模型，將宏觀、細觀尺度結合起來進行研究。

從細觀力學角度研究巖石的破壞規律，對進一步認識巖體的力學特性，保障巖體工程的安全穩定性具有重要意義。Brace等[10]最早對翼裂紋進行觀測試驗，研究了壓力作用下裂紋的擴展規律。許江等[11]利用自主研發的煤巖雙面剪切細觀開裂演化過程裝置，通過開展不同速率條件下的剪切試驗，對砂巖細觀開裂過程、細觀開裂擴展空間分布進行了深入研究。唐海等[12]采用三軸壓縮設備對砂巖進行特定高圍壓下不同軸向壓力加載試驗，研究了砂巖在特定高圍壓下的細觀損傷特征。Hu等[13]以小孔隙沉積巖為研究對象，在不同初始加載應力變量基礎上進行單軸壓縮，利用核磁共振測量巖石試樣加載前、后的變化，建立了細觀損傷與宏觀力學參數特征的關聯函數。張國凱等[14]運用數值模擬軟件研究了巖石細觀特征與宏觀破壞的影響。宮偉力等[15]以工業電子計算機斷層掃描(CT)為探測手段，對含氣煤巖進行三軸加載試驗，并利用數字圖像處理技術對三軸條件下煤巖細觀損傷破壞的規律進行分析，探究了煤巖變形破壞的規律。倪驍慧等[16]對花崗巖進行細觀疲勞損傷量化試驗研究，通過疲勞損傷信息的量化和統計分析，定量分析了花崗巖循環荷載作用過程中的細觀損傷特征。文獻[17-20]中對凍融條件下的巖體細觀損傷特征進行了研究。

大理巖是我國西部水電工程中常見的巖體，研究大理巖的裂紋擴展機理進而探索大理巖的變形破壞規律，對保證水電站工程結構安全具有重要意義。目前對砂巖、煤巖等巖石的細觀損傷研究較多，而對大理巖進行細觀損傷的研究較少。本文中以四川雅礱江錦屏二級水電站大理巖為研究對象，對包含預制裂紋的大理巖進行細觀損傷試驗，應用掃描電子顯微鏡(SEM)對大理巖試件受壓過程中割縫兩端產生的翼裂紋進行實時觀測，對翼裂紋的擴展進行定量化描述，揭示大理巖的細觀損傷演化規律。

1 翼裂紋擴展觀測試驗

1.1 試件制備

巖石試樣是采自四川雅礱江錦屏二級水電站工地現場的大理巖。錦屏二級水電站位于四川涼山雅礱江干流之上，裝機容量為4.4×106kW，電站由首部低閘、引水隧洞、地下廠房3個部分構成。隧洞長度為16～19 km，直徑為11 m，一般埋深為1 500～2 000 m，最大埋深為2 500 m，是洞線長、洞徑大、埋深極大的大型引水隧洞，是該水電站的關鍵部分之一。大理巖取樣的主要性質如表1所示。

表1 大理巖取樣的主要性質

試驗共加工5個試件，分別編號為1—5。將巖石加工成尺寸為20 mm×10 mm×2 mm(長度×寬度×厚度)的試件。為了減少對試件的破壞，采用超聲波打孔，在巖板中間預制一條橢圓裂紋。裂紋長軸長度為4 mm，短軸長度為0.5 mm，角度為45°。預制裂紋試件示意圖與實物圖如圖1所示。

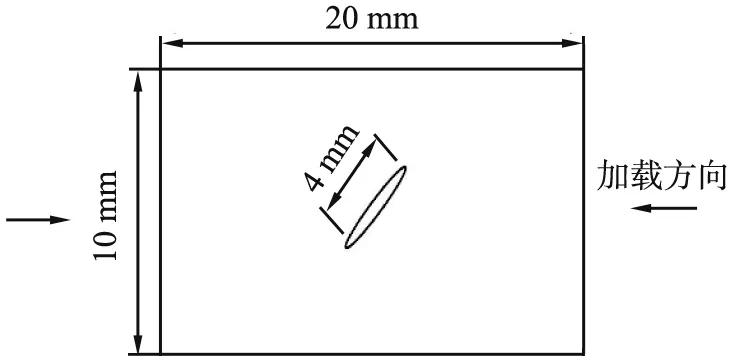
(a)示意圖

(b)實物圖圖1 預制裂紋試件示意圖與實物圖

1.2 試驗設備

采用SEM(升級改造后的S-570型，日本Hitachi公司)對加載過程中試件變形、損傷、斷裂形態與力學量進行實時觀測。加載裝置拉伸臺的參數如下：載荷范圍為0～2 000 N，拉壓行程為0～10 mm。

1.3 試驗過程

由于大理巖不導電，利用SEM進行觀測時容易發生電荷積累，因此需要對試件表面進行鍍金處理。將試件放置到拉伸臺上，利用控制器進行加壓，在加壓過程中獲取巖石細觀結構圖像。

試驗開始時，以加壓步長100 N進行加載。當微裂隙出現較多時，縮小加壓步長至50 N，直至試件破壞。試件受壓加載過程如圖2所示。

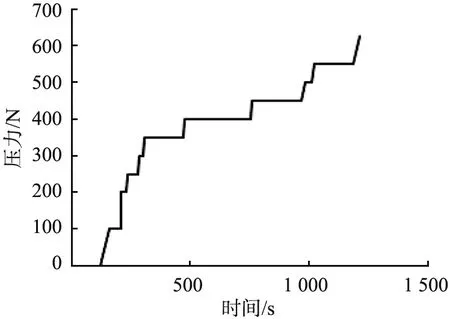
圖2 試件受壓加載過程

2 圖像處理與參數獲取

2.1 圖像處理

由SEM獲取的細觀圖像是8位灰度的二維圖像，一張8位灰度的二維圖像可以看作一個矩陣[21]，其中每個矩陣的單元即為圖像中的一個像素點，像素值f(x,y)為坐標(x,y)處的灰度，f(x,y)反映(x,y)處的亮度，f(x,y)的變化范圍為0～255。

為了識別圖片中的裂紋進而獲取信息，采用閾值分割法對原始圖像進行分割。在MATLAB軟件中，二值圖像是一個邏輯類，僅包括0和1這2個數值，像素0顯示為黑色，像素1顯示為白色。使用二值化函數im2bw并且設定合適的閾值可以將灰度圖像轉化成為二值圖像。

2.2 參數獲取

MATLAB軟件中的bwlabel和regionprops函數可以對二值化圖像里的裂紋或顆粒進行標識并統計各參數值。由這些參數值可以獲得顆粒或空隙的空隙率、面積、周長、形狀系數、扁圓度和方位角等。

1)面積。MATLAB軟件通過統計像素個數來統計面積，可以由構成裂隙的像素個數和放大倍數計算得到裂隙的實際面積。

2)長度。MATLAB軟件所返回的裂隙的長度為裂隙外接橢圓的長軸的長度。

3)方位角。MATLAB軟件所返回的方位角指橢圓長軸與水平線之間的角度，逆時針為正，順時針為負，取值范圍為-90°～90°。

3 結果與分析

3.1 翼裂紋擴展定性描述

圖3所示為試件由加載開始直至破壞的過程。在未加載時，預制割縫的端部沒有發現裂紋(見圖3(a))。隨著試件的加載，在接近預制割縫尖端的拉應力集中部位出現1條微裂紋，方向大致與預制割縫垂直(見圖3(b))。隨著荷載逐漸增加，在已存在微裂紋附近區域產生了較多新的彌散微裂紋。如此反復，幾條微裂紋匯集成2條較長、較寬的微裂紋。當荷載增加至更高水平時，新生微裂紋的方向由大致垂直于預制割縫方向逐漸向加載軸方向轉動(見圖3(c))。當應力達到某臨界值時，主裂紋形成，巖體突然發生破壞(見圖3(d))。

損傷的演化產生一種特殊的力學響應，即應力集中消弛現象，伴隨損傷演化過程，原有的局部應力集中發生調整、消散和轉移。應力集中消弛在試驗中表現為裂紋1的擴展影響到裂紋2的擴展，裂紋1的擴展最終造成裂紋2的彌合，如圖4所示。

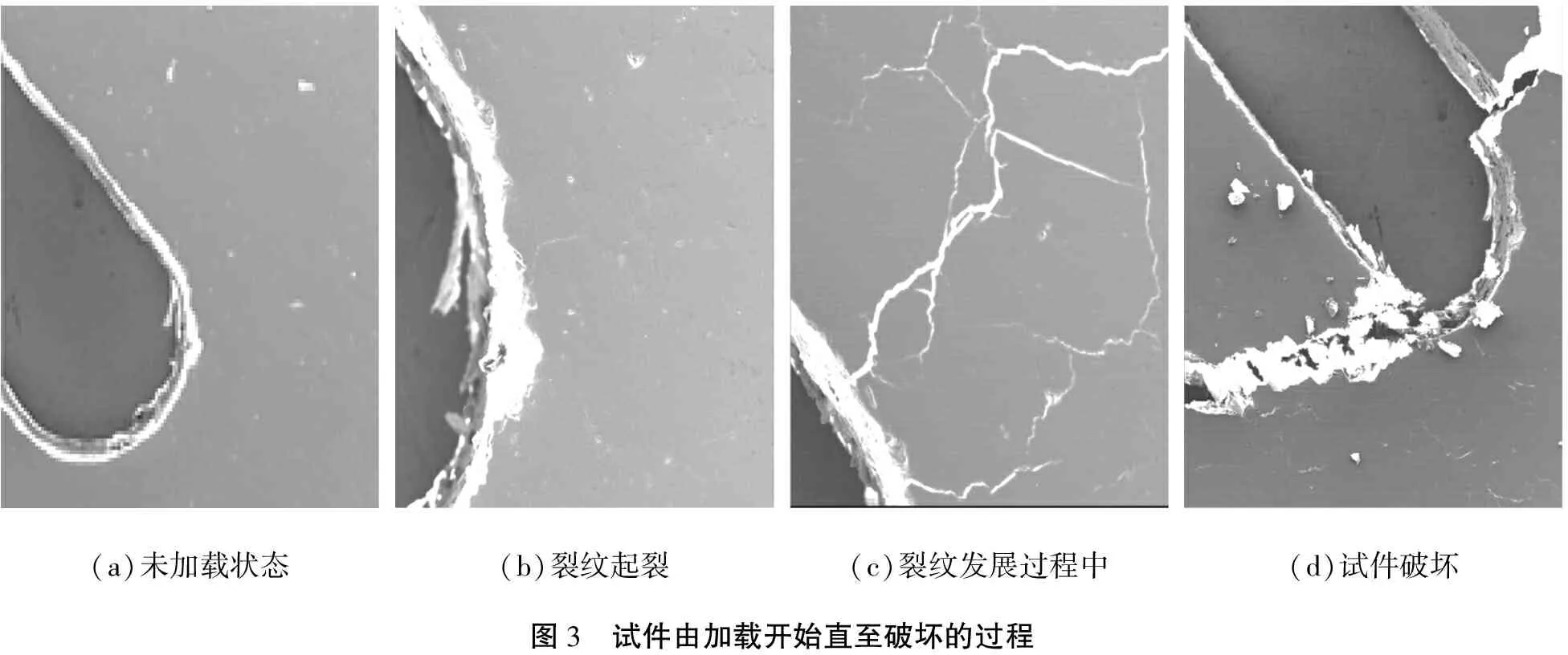
(a)未加載狀態(b)裂紋起裂(c)裂紋發展過程中(d)試件破壞圖3 試件由加載開始直至破壞的過程

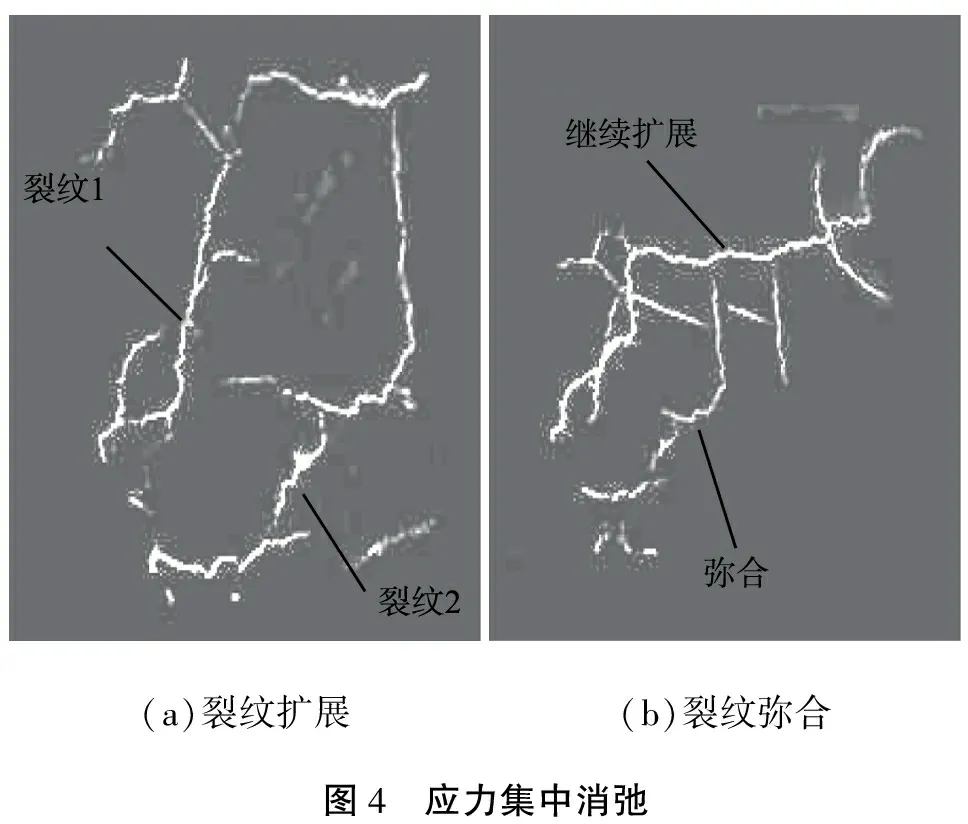
(a)裂紋擴展(b)裂紋彌合圖4 應力集中消弛

3.2 翼裂紋擴展量化描述

對翼裂紋的細觀圖像進行二值化處理后，提取翼裂紋方位角、長度、面積等參數，進而獲得微裂紋諸參數的變化規律。圖5所示為試件5的翼裂紋隨著應力的增大而擴展的過程圖像。以試件5為例，對翼裂紋擴展過程的裂紋方位角、長度、面積進行量化描述。

3.2.1 平均偏轉角

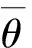
(1)

式中：i為裂紋編號，i=1，2，，n，n為正整數；li為微裂紋的長度；θi為微裂紋的角度。

(a)應力為17.5 MPa(b)應力為20.0 MPa(c)應力為22.5 MPa(d)應力為25.0 MPa(e)應力為27.5 MPa圖5 試件5的翼裂紋隨著應力的增大而擴展的過程圖像

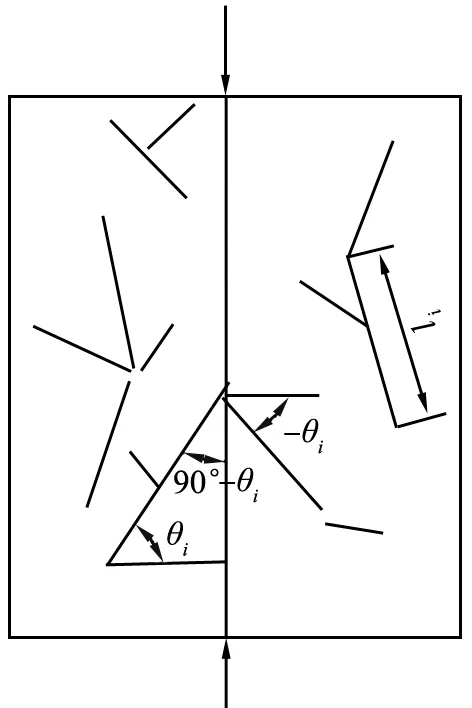
i—裂紋編號，i=1，2，，n，n為正整數； li—微裂紋的長度； θi—微裂紋的角度。圖6 裂紋傾角示意圖

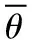
表2 加載過程中裂紋平均偏轉角的變化

3.2.2 微裂紋長度

在宏觀裂紋未形成之前，隨著應力的增大，微裂紋的總長度持續增加，并且有一個加速的過程，如圖7(a)所示。

3.2.3 微裂紋面積

在宏觀裂紋未形成之前，微裂紋的總面積持續增大，并且有一個加速的過程，面積增加的速度大于長度增加的速度，如圖7(b)所示。

3.3 翼裂紋擴展過程分形特征分析

分形是對沒有特征長度但有某種意義下自相似的形體和結構的總稱[22]。應用分形幾何可以實現定量描述裂紋擴展的路徑，建立裂紋擴展的分形模型。

3.3.1 翼裂紋自相似擴展的模式

通過對幾個試件翼裂紋擴展的觀察和研究，得到翼裂紋自相似擴展的模式如下：

1)裂紋在擴展過程中曲折前進，但是并非毫無方向，由裂紋擴展的細觀圖像可以看出，裂紋擴展都有一個基本方向。

2)每級分叉角大體相同，不會隨著裂紋的擴展有很大的變化。

3)上一級裂紋會分叉成為2個分支，但是在裂紋的發育過程中并不是2個分支都會充分發育，而是一支發育得相對充分，另一支發育得較緩慢和不充分，導致未充分發育的那一支不再進行分叉，而發育充分的那一支會在合適的時間再進行分叉，周而復始，形成裂紋網絡。翼裂紋發育抽象示意圖如圖8所示。

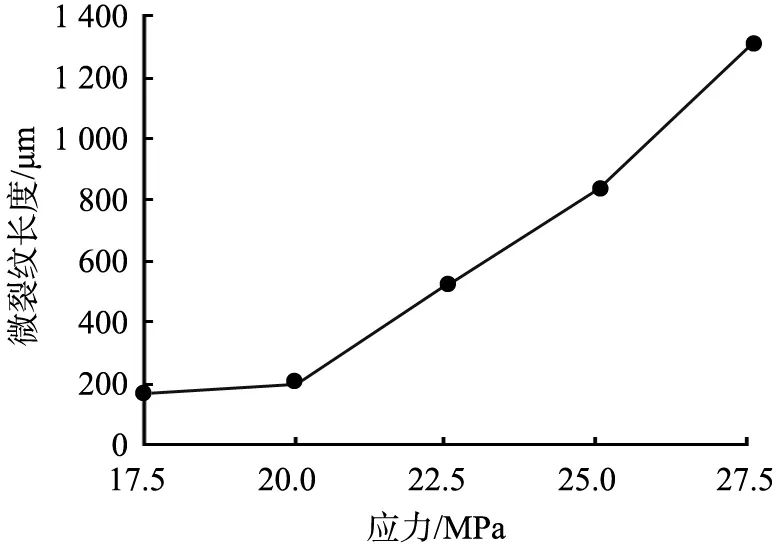
(a)長度與應力的關系

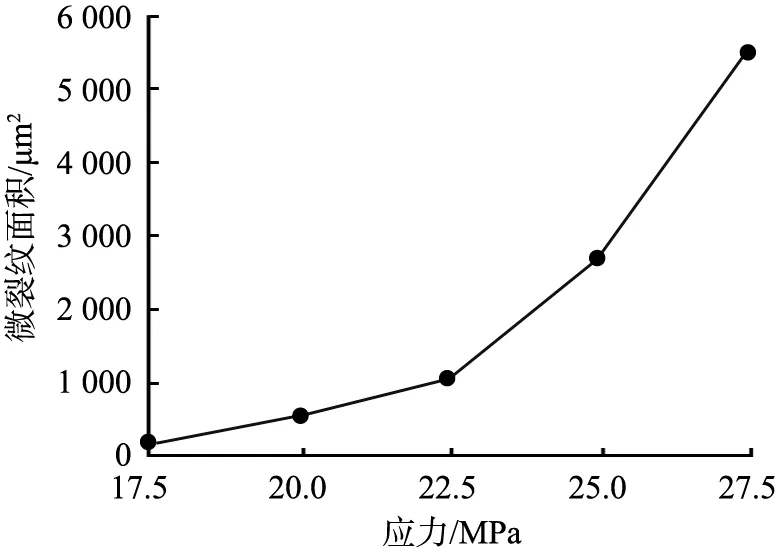
(b)面積與應力的關系圖7 微裂紋長度、面積與應力的關系

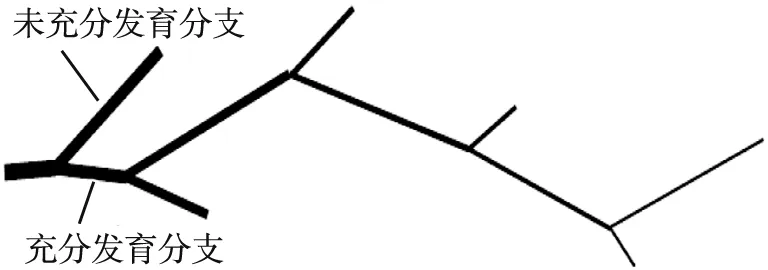
圖8 翼裂紋發育抽象示意圖

3.3.2 翼裂紋擴展過程中分維數變化

分維數是用于描述分形的特征量。利用盒維數法對各應力水平下的翼裂紋分維數進行計算，結果如表3所示。

由于試件2、4、5經過的荷載級數較多，因此選取試件2、4的下翼裂紋、試件5的上翼裂紋進行分析，得到翼裂紋的分維數變化趨勢，如圖9所示。由圖可知，前期3個試件的分維數增長較快，試件5后期的分維數增長速度放緩，試件2、4的分維數甚至減小。這是由于分維數是一個反映裂紋網絡復雜程度的參量，在前期，裂紋網絡迅速擴大，網絡復雜程度增強，而在后期，一些發育成熟的裂紋相互匯集，寬度增加，但是復雜程度明顯降低，因此裂紋網絡的分維數增長放緩甚至減小。

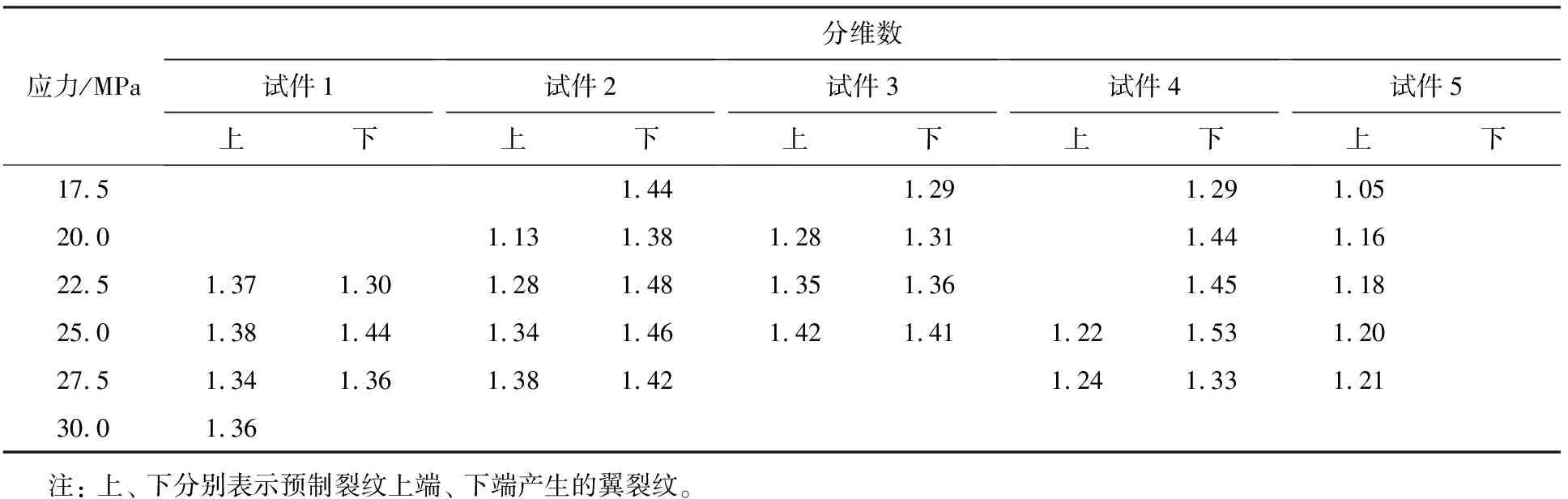
表3 不同應力水平下的翼裂紋分維數

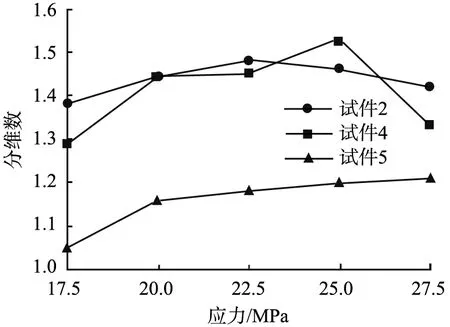
圖9 翼裂紋分維數變化趨勢

3.3.3 斷裂韌度與裂紋分叉角之間的關系

用自相似分形模擬裂紋分叉，建立裂紋分叉的分形模型，如圖10[23]所示。

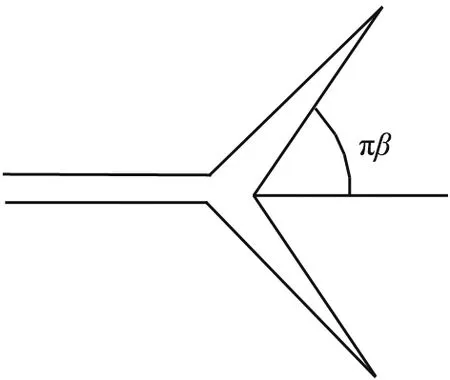
β—裂紋的分叉角。圖10 裂紋分叉的分形模型[23]

根據分形幾何原理和裂紋發展的主方向，利用生成元得到

D=lgN/lg (r-1)，

(2)

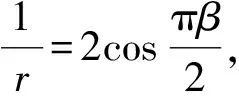
裂紋的擴展力G為

G=2γd1-D-G0d1-D，

(3)

式中：γ為單位宏觀量度的表面能；d為晶粒尺寸；G0為考慮分叉幾何非規則分形效應的裂紋擴展力。

由斷裂力學原理，斷裂韌性與裂紋擴展力的對應關系為

(4)

其中，在平面應變狀態下

(5)

在平面應力狀態下

(6)

式中：K為斷裂韌性；K0為未考慮分叉幾何非規則性分形效應的斷裂韌性；E為楊氏模量；υ為泊松比。

由式(2)、(4)可以計算在微觀情況下裂紋分叉模型的裂紋分叉角的變化對裂紋斷裂韌性的影響。由斷裂韌性計算結果可以發現，斷裂韌性隨著裂紋分叉的夾角增大而改善，表明裂紋分叉的夾角越大，所需耗散的能量釋放越多，裂紋分叉角較大時的斷裂越難產生。

各試件的分叉角與最終斷裂應力如表4所示。

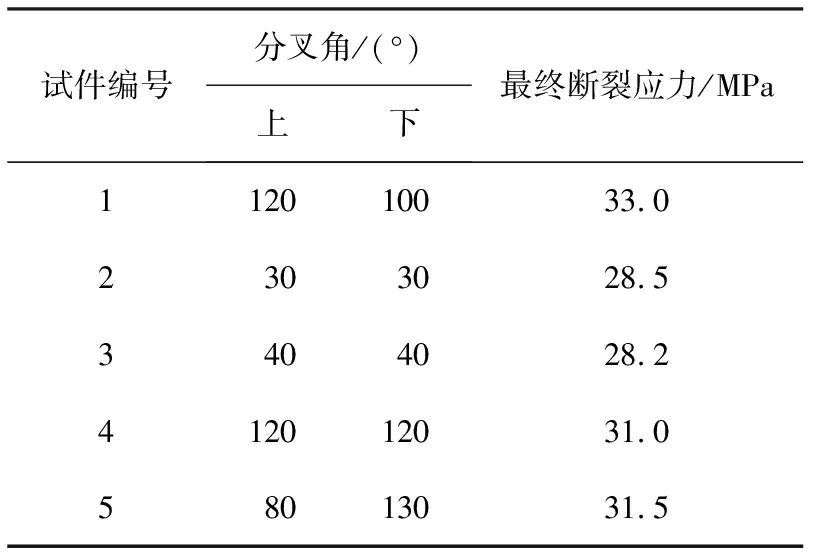
表4 試件的分叉角與最終斷裂應力

由表可知，試件1、2、5的分叉角較大，最終斷裂應力也較大。試件1的分叉角約為試件2分叉角的4倍，而試件1的最終斷裂應力比試件2大15.8%。斷裂應力較大說明試件的斷裂韌度也較大，驗證了關于分叉角同斷裂韌度的關系的理論。

4 結論

本文中通過開展大理巖細觀損傷試驗，對受壓狀態下大理巖預制裂紋試件進行實時觀測；對不同壓力時的細觀圖像進行分析處理，得到清晰的翼裂紋圖像，并由此提取細觀信息，從而對翼裂紋的發展進行了定性和定量的分析。主要結論如下：

1)利用SEM對割縫兩端產生的翼裂紋進行動態觀測，得到了不同壓力時的翼裂紋圖像。運用數字圖像處理技術對巖石細觀結構圖像進行處理，并編程實現從二值化圖像中提取巖石細觀結構面的微裂隙長度、方位角、面積等信息。

2)隨著荷載的增加，首先在預制割縫尖端附近產生近似垂直于割縫的微裂紋，然后在微裂紋附近產生較多彌散微裂紋，匯集成為2條較長、較寬的微裂紋。當壓力達到一定的值時，主裂紋產生，巖體突然發生破壞。

3)裂紋的偏轉角隨著應力的增大而減小，表明裂紋的發展是趨向于主應力方向的。裂紋的長度和面積隨著應力的增大而持續增加，并且表現為一個加速的過程。

4)用分形理論對翼裂紋進行研究，發現翼裂紋是以自相似方式演化的。提出翼裂紋分形擴展的模式。計算各應力時的分維數，得到分維數變化的規律。試件分叉角越大，對應的斷裂韌度及斷裂時的最終應力也越大。