基于八叉樹優化的MoM-PO/PTD混合算法分析目標電磁散射及輻射問題

李弘祖, 郭立新, 董春雷, 孟 肖

(西安電子科技大學物理與光電工程學院, 陜西 西安 710071)

0 引 言

在針對電大物體開展電磁散射特性的分析過程中,一般選擇使用高頻算法,比如物理光學(physical optics,PO)法、幾何光學(geometrical optics, GO)法[1]、幾何繞射理論(geometrical theory of diffraction,GTD)[2]、一致性GTD(uniform GTD,UTD)[3]、物理繞射理論(physical theory of diffraction, PTD)等。這些算法都把物體的各個部分分解出來,任一部分的散射特性跟剩余部分沒有關聯。所以,針對某個部分的散射場開展研究只需要考量入射波,可以不考慮剩余部分的耦合。盡管有效降低了計算難度,然而針對復雜度較高的結構計算出的結果精度不高[4]。對于低頻方法,以矩量法(method of moments, MoM)[5]為例,其計算結果較為精準,但由于計算所需的時間較長以及計算機內存需求較大,一般只應用于計算電小尺寸的結構,而遇到復雜目標的電磁散射問題時,需要采用高低頻混合的方式來解決。Jakobus[6]針對MoM和PO混合使用的理論進行描述,并在環境較為復雜的電磁散射中進行使用;Wang[7]將等效偶極子與迭代式MoM-PO混合算法相結合,計算了電大目標的電磁散射特性;Tong[8]成功將改進后的MoM-PO算法應用于目標和隨機二維介質粗糙面的計算。

MoM的計算結果精度高,能夠應用于復雜精細結構的計算。PO方法將散射源從物體本身換成了散射物體表層感應電流,隨后通過電流積分計算出散射場的分布。該方法計算資源需求低、速度快,但無法精確地計算復雜結構[9-10]。因此,基于電流基的MoM和PO的混合算法[11-13]在求解電大尺寸目標散射和電大載體附近天線輻射問題中得到了廣泛的應用。由于PO方法無法計算目標的棱邊繞射問題,因此計算結果存在誤差。鑒于此,利用PTD手段對目標區域的棱邊繞射場開展計算,提高了在計算目標散射和輻射時的精準度。

此外,在計算PO區域時,傳統面元遮擋判斷算法的時間成本較大,因此,本文提出了基于八叉樹優化的MOM-PO/PTD快速混合算法,將八叉樹和后向追蹤[14]算法應用于PO區域面元的遮擋判斷。相較于標準射線追蹤計算方法,八叉樹開展優化以后的追蹤手段不再選取面元作為基本單位跟剩余面元開展比較評估,所以極大地減少了計算工作量,避免了資源的浪費。最后文中將修正后的計算結果與數值方法相比較,驗證了該方法的有效性,同時與未采用八叉樹的混合方法相比較,結果顯示本文算法使計算效率大大提升。

1 基本理論

應用MoM-PO混合法[15-20]首先需要將計算模型分為兩個區域[21]:MoM區域和PO區域。MoM的計算結果比較精確,一般將激勵源附近、電尺寸較小、邊緣和棱邊較多的區域劃分為MoM區,將電大尺寸平滑結構劃分為PO區。如圖1所示。

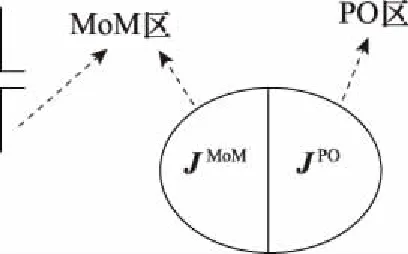
圖1 MoM區域和PO區域分區

將MoM區域的電流設為JMoM,將PO區域的電流設為JPO。根據RWG基函數[22]將JMoM和JPO展開為

(1)

(2)

式中：NMoM和NPO分別為MoM區和PO區域RWG基函數數目,αn和γn分別為JMoM和JPO的展開系數。

根據高頻近似條件,PO照明區的表面電流為JPO=2n×Hi,計入MoM區域產生的磁場對PO區域的影響,則電流可以表示為

(3)

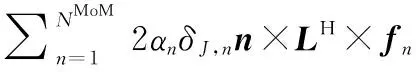
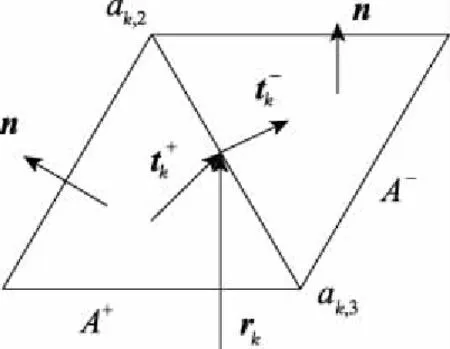
圖2 在公共邊上引入矢量

由RWG的性質可知,在第k條邊的中點處有[11]:

(4)

(5)

其中k=1,2, …,NPO為PO區未知數的個數。將式(3)代入式(5)得

(6)

式中:

(7)

(8)

最后,在MoM區建立電場積分方程[23]:

(LEJMoM)tan+(LEJPO)tan=-Etan

(9)

將式(1)和式(2)代入式(9)得

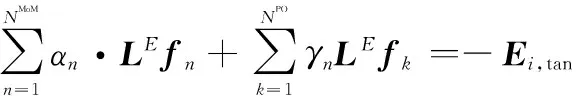
(10)

通過GalerKin法,可以得到如下線性方程組:

(ZMoM+ZMoM,PO·τk,n)·IMoM=V-ZMoM,PO·τk

(11)

其中,ZMoM=〈fm,LEfn〉,ZMoM,PO=〈fm,LEfk〉,V=〈fm,E〉。

在進行MoM位置電流的計算過程中,通過使用迭代的方式,計算得到矩量區域電流以后,將計算得到的電流系數代入公式(3)中,從而計算出PO區域的電流系數;再對電流進行積分便可得到目標的散射場和輻射場;最后,將兩區域的場進行疊加,便可得到總的場強。

2 算法描述

2.1 八叉樹的構造原理及應用

八叉樹也被叫做八元樹,是一種效率較高的空間層次樹狀構造,可以有效降低計算方法在空間層面上的復雜程度。八叉樹的剖分均依據八分標準,可以將其看做四叉樹構造進行拓展獲取到的三維空間[24]。

在所需計算的空間中,八叉樹剖分的過程是首先將復雜場景內所有點放在三維坐標系中,得到X,Y,Z分量上的極限大小值,以這些極限值構建一個包圍整個場景的空間,并從3個方向將空間分割為大小一樣的八個子空間,形成一組八叉樹。針對某個包圍盒開展進一步剖分的基礎是這一空間內含有的三角面元數大于預設的閾值。八叉樹的各個非葉節點都存在零個或八個子節點,一般把它們利用A,B,C,D,E,F,G,H進行記錄。假如未能達到深度的最大值,那么開展進一步的劃分[25]。

標準射線追蹤方法是對所有面元一一進行明暗判定,相比于傳統的射線追蹤算法,經過八叉樹改進后形成的射線追蹤算法不再選取一個基本面元作為單位和其他面元進行明暗判定,而是先判斷此包圍盒所在空間中的位置,然后再判斷處在該包圍盒內的面片是否被遮擋。這一方法極大地減少了計算工作量,避免了資源的浪費。

該算法的步驟如下:假設一簇平行入射波方向為r=(ex,ey,ez),面元S的法向方向為n,重心坐標為P0=(x0,y0,z0),某一包圍盒在XYZ方向上的最大值、最小值分別記為:Xmax、Ymax、Zmax、Xmin、Ymin、Zmin,則面元S被入射波照亮需要滿足以下兩個條件:

條件 1入射波方向r與面元S的法向量n應滿足:rn<0;

條件 2入射波照射到面元S時沒有被其他面元遮擋。

使用如下方法對條件2進行判斷:從面元S的重心處發射一條射線,方向與入射射線方向相反,追蹤此射線并判斷其是否與其他面元相交。具體步驟如下:

設面元S上的出射射線起始位置為P0,方向為-r=(mx,my,mz)。先分析這一射線方向跟包圍盒所處的位置會不會發生重疊。射線通過某個包圍盒內部所滿足的條件為:

(1)當mx>0時,Xmax>x0;

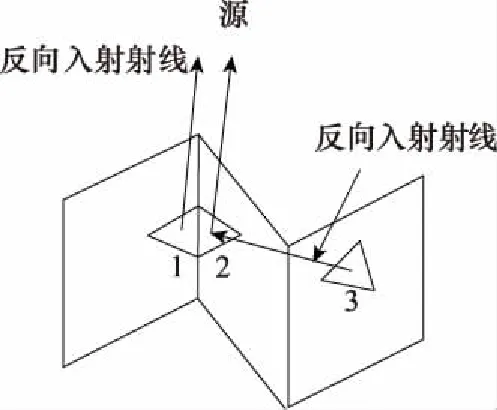
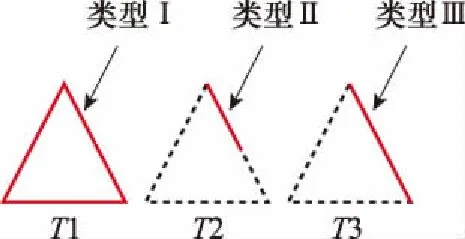
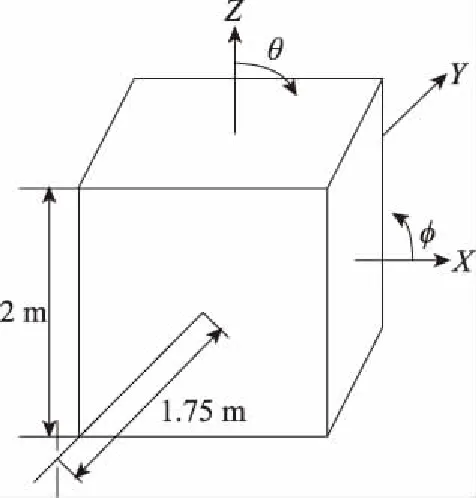
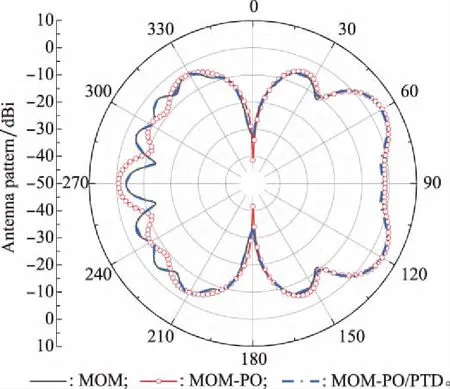
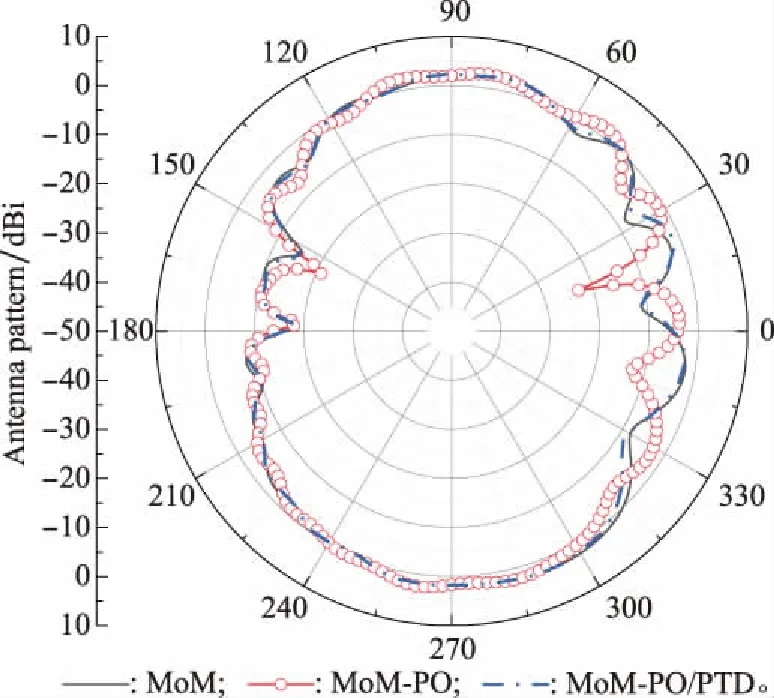
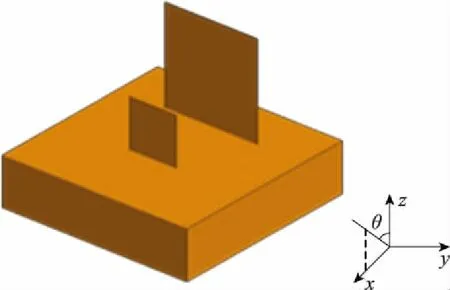
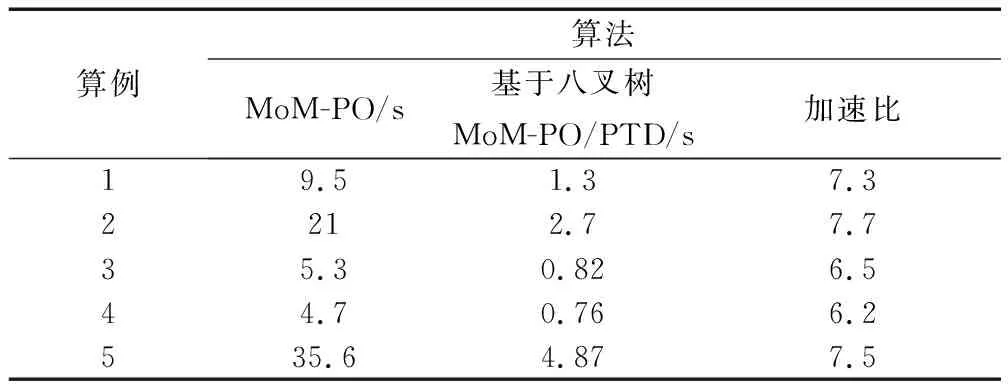
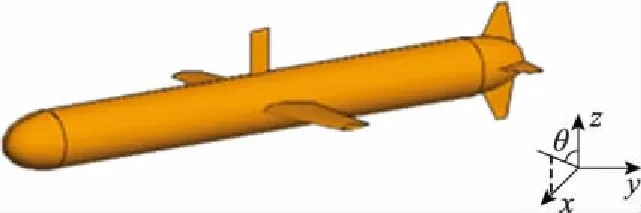
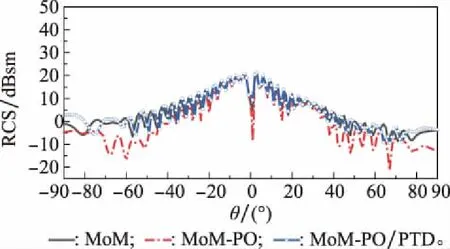
(2)當mx<0時,Xmin

(3)當my>0時,Ymax>y0;

(4)當my<0時,Ymin

(5)當mz>0時,Zmax>z0;

(6)當mz<0時,Zmin

輻射上述條件的前提下,再依據條件1分析這一射線跟包圍盒中含有的面元是否會出現相交,如果存在一個面元與其相交,而且交點位置在面元當中,這說明面元m的位置在暗處,反之,其所在位置為亮處。

2.2 后向追蹤原理及應用

在射線追蹤的過程中,往往會面臨射線管分裂和難以判斷照射區域這兩問題,為解決此類問題,本文采用后向追蹤方法。

和傳統的射線追蹤算法相比,后向追蹤算法摒棄了虛擬射線管。所采用的方法是:首先,將目標模型網格劃分為三角形后,記錄這些三角形面片及其3個相鄰面片的ID并存儲在計算機內存中。其次,將每一個面元的中心作為射線的發射點,射線的方向為入射波的反方向,并沿著與此方向向源追蹤。因此,判斷該面元是否被照亮的條件是在進行射線追蹤的過程中,此射線不被其他面元遮擋。如圖3所示,編號為1和2的兩個面元使用后向射線追蹤算法,使得射線管分裂的問題得到有效解決。

圖3 后向追蹤技術示意圖

2.3 利用PTD修正PO區電流

在計算具有精細結構的復雜目標電磁特性時,傳統的MoM-PO的混合算法通常具有很大的優勢,但PO算法無法計算目標棱邊的繞射場同時將陰影區電流等效為零,這與實際電流的分布情況存在差異,造成MoM-PO混合算法的計算目標散射與輻射特性時存在一定的誤差。考慮到上述因素的影響,本文利用PTD[26]對PO區域的電流進行修正,在分析復雜結構目標的電磁特性問題時,將混合算法與PTD相結合,計入棱邊繞射場對計算結果產生的影響,結合常用的計算模型,經過將該算法結果跟數值結果的對比,對該算法的有效性進行驗證,有效拓寬了MoM-PO混合算法的應用范圍。常見的劈形結構如圖4所示。

圖4 電磁波照射到一個典型目標上

應用PTD,得到其遠區散射場計算公式為

(12)

式中:Ie和Im分別表示等效電流和等效磁流,表達式為

(13)

(14)

在實際應用PTD算法的過程中,往往需要判斷經三角形剖分后的目標,其三角形的各邊能否構成劈形結構,如圖5所示。當相鄰的面元與之間處于同一個平面內并且不構成目標的棱邊時,不存在棱邊繞射現象;對于具有公共邊的一對三角面片,當它們構成劈形結構且兩面片均被照亮時,目標的棱邊繞射場為總場的二分之一,但當其只有一個被照亮時,棱邊繞射場可由(12)式得出。

圖5 將三角形的棱邊分為三類

將PO散射場和3個棱邊的繞射場相疊加,便可得到修正后的PO區域總的散射場。其中,PO散射場可根據JPO求得。棱邊的繞射場主要由入射電磁場以及MoM區域與PO區域的耦合電磁場所產生。入射電磁場所產生的棱邊繞射場可由式(12)求得。

記耦合電磁場所產生的電磁場為EMoM,可表示為

EMoM=LE(JMoM)

(15)

LE(X)=

(16)

將式(1)代入(16)即可求得EMoM,再將式(15)代入式(12),求解得到MoM區域與PO區域的耦合電磁場所產生的棱邊繞射場。最后,將PO位置所含的三角面片計算得到的散射場開展矢量相加,結果就是總的散射場。

3 數值算例

3.1 MoM-PO算法計算載體上方天線方向圖

為了對該算法的有效性開展驗證,首先對電大載體平臺影響線天線方向圖的情況開展分析,并跟MoM算法開展對比。

算例一為2 m×2 m×2 m的立方體前方1.75 m處有一半波對稱振子天線,天線的工作頻率f為1 GHz,如圖6所示。計算時選擇天線為MoM區,立方體為PO區。分別采用傳統混合方法和改進后的計算方法計算,總的未知數目2 650。兩種計算方法的運行時長和輻射方向分別通過表1和圖7獲取。由表1可以看出經過八叉樹和后向追蹤優化的算法,在判斷面片的遮擋時所需時間明顯減少,時間加速比為7.3。在圖7中,黑線和藍線分別表示MoM和MoM-PO/PTD方法的計算結果。由圖7可以看出,MoM-PO/PTD和MoM算法吻合較好,表明經過PTD算法的修正,在210°～300°附近,天線方向圖的誤差明顯減小,計算精度有了顯著提高。

圖6 天線位于立方體前

圖7 位于立方體前的天線方向圖

算例二為半波對稱振子天線位置與5 m×2 m×2 m的簡易船模型上方2 m處,天線的工作頻率f為1 GHz,如圖8所示。計算時選擇天線為MoM區,而船為PO區。分別采用傳統混合方法和改進后的計算方法計算,總的未知數目5 430。兩種算法的運行時間由表1給出,時間加速比為7.7。天線的輻射方向圖由圖9給出,其中,黑線表示MoM計算結果,藍線表示本文算法計算結果。可以看出,本文算法和MoM算法吻合較好,結果表明天線方向圖在-30°～30°范圍內的誤差減小,計算精度顯著提高。

圖8 天線位于艦船上方

圖9 位于艦船上方的天線方向圖

3.2 MoM-PO算法計算散射場

算例三為底面尺寸2 m×2 m×0.5 m的立方體,上方為0.5 m×0.5 m和1 m×1 m的兩個平板,如圖10所示。計算時選擇立方體上方兩平板為MoM區,其余部分為PO區,總的未知數目為1 524。采用平面波照射,入射角θ=-90°～90°,φ=0°,入射波頻率f=1 GHz,極化方式為HH極化。表1給出了兩種算法的運行時間,時間加速比為6.5。圖11給出了傳統混合算法和修正后混合算法與MoM算法的單站散射場計算結果比較,其中,黑線表示MoM計算結果,藍線表示本文算法計算結果,可以看出,本文算法和MoM算法吻合較好。

圖10 底面長方體及上面兩平板

表1 算法運行時間比較

圖11 立方體上兩平板的單站RCS結果

算例4為長為3 m的導彈模型,如圖12所示。計算時選擇導彈兩翼和尾翼為MoM區,其余部分為PO區,總的未知數目為1 200。采用平面波照射,入射角θ=-90°～90°,φ=0°,入射波頻率f=1 GHz,極化方式為HH極化。兩種方法的計算時間由表1給出,時間加速比為6.2。由圖13可以得出在計算較為復雜的模型時,該算法同樣具有較高的精度。

圖12 導彈模型

圖13 導彈模型的單站RCS結果

算例5為5 m×1 m×1 m的艦船,如圖14所示。計算時選擇甲板上方為MoM區域,其余部分為PO區域,總未知數為7 646。采用平面波照射,入射角θ=-90～90°,φ=0°,入射波頻率f=1 GHz,極化方式為HH極化。表1給出了兩種算法的運行時間,時間加速比為7.5。圖15給出了傳統混合算法和修正后混合算法與MoM算法的單站散射場計算結果比較,其中,黑線和藍線分別描繪的是利用MoM算法和本文算法得到的結果,能夠發現,本文算法跟MoM算法具有很好的吻合度,從而對本文算法的有效性進行了驗證。

圖14 艦船模型

圖15 艦船模型的單站RCS結果

4 結 論

本文針對電大載體平臺上的線天線輻射問題以及目標的電磁散射問題,提出了基于八叉樹的MoM-PO/PTD快速混合算法。從文中所給的算例以及表1可以看出該算法計算所需時間大幅減少,時間加速比為6～7倍。與此同時,采用PTD算法進行修正后目標的散射以及輻射的計算精度有了明顯提升。