橢球顆粒體系剪切過程中自由體積的分布與演化1)

鄒宇雄 馬 剛,2) 李易奧 王 頔 邱煥峰 周 偉

* (武漢大學水資源與水電工程科學國家重點實驗室,武漢 430072)

? (水工巖石力學教育部重點實驗室,武漢 430072)

** (中國電建集團貴陽勘測設計研究院有限公司,貴陽 550081)

引言

顆粒物質是由大量離散固體相互作用而形成的復雜體系,在自然界和工業界廣泛存在.以水利和巖土工程中的堆石體為例,由于取材方便,且對地形、地質條件有較強的適應性,在堆石壩、路堤、機場高填方地基等工程建設中得到廣泛應用.這些工程一旦出現問題和隱患,將會嚴重威脅人民生命財產安全,因此迫切需要深入研究顆粒材料的物理力學特性.

由于顆粒材料具有結構異質性、各向異性和多尺度結構等特點,其表現出復雜的物理力學特性,如剪脹[1]、應變局部化[2],固?液轉變[3-4]等.對巖土類顆粒材料,自1963 年Roscoe 等[5]提出劍橋模型以來,許多學者根據顆粒材料的宏觀應力變形特性發展了各種各樣的本構理論[6-8].但目前還沒有統一的理論能夠解釋顆粒材料所有的應力變形特性.蔣明鏡[9]指出這些基于唯象的土力學本構理論雖然在巖土工程實踐中發揮了重要作用,但是難以從機理上刻畫巖土顆粒系統的非連續性、大變形、破壞等問題.因此,越來越多學者嘗試從細觀尺度研究顆粒材料復雜力學行為的起源,并試圖將顆粒形狀、表面摩擦、粒徑分布等顆粒尺度的特性與宏觀力學響應建立聯系.

巖土顆粒材料的形狀各異,大量研究表明顆粒形狀對顆粒材料的剪切強度[10-13]、塑性行為[14]以及堆積特性[15-16]等有顯著影響.深入研究顆粒形狀對顆粒材料物理力學特性的影響,剖析這些影響的細觀機理,對顆粒材料的理論研究和工程應用有重要意義.受試驗技術限制,目前只能通過光彈試驗技術[17]、X-ray 斷層掃描技術[18]等研究顆粒材料宏觀力學響應的細觀機理.與此同時,細觀數值模擬方法在顆粒材料的宏細觀力學特性研究方面得到廣泛應用,如離散單元法(discrete element method,DEM)[19]和連續離散耦合分析方法(combined finite and discrete element method,FDEM)[20-21].其中FDEM 中將顆粒離散為有限元網格,理論上可以考慮任意顆粒形狀,在模擬復雜顆粒形狀方面具有顯著優勢.

雖然顆粒材料的結構特性與其物理力學性質的相關性已經得到大量研究證明[22-26],但是具有復雜顆粒形狀和寬粒徑分布的顆粒材料的結構表征,以及建立宏觀力學響應和細觀結構的聯系仍是一個重大挑戰.基于該現狀,顆粒統計力學得到了快速發展,例如Edwards 等[27-28]建立了顆粒系統的體積系綜理論(Edwards' volume ensemble),用統計物理的框架來研究非平衡態的顆粒堆積問題.該理論強調了局部自由體積(孔隙)在描述靜態顆粒材料阻塞行為中的重要作用.在工程中,常采用孔隙率、孔隙比、體積分數等表征顆粒材料的密實程度,但是這些表征量僅能提供宏觀尺度的自由體積信息,忽視了顆粒尺度自由體積的形態、分布和演化.

已有研究表明,顆粒尺度的自由體積與顆粒材料的力學性能、變形特征等密切相關[29-30],所以有必要探索顆粒材料的自由體積的統計分布特性及其在剪切過程中的演化規律.將顆粒與其周圍的自由體積組成一個局部元胞(以Voronoi 元胞較為典型)用以定量分析顆粒材料自由體積特征是一種常見思路.不少學者研究了顆粒材料在特定狀態下的局部自由體積[31-32].但是顆粒材料在剪切過程中會產生顆粒重排列現象,顆粒材料的細觀結構和自由體積會不斷演化.因此,探索剪切過程非球顆粒材料的局部自由體積的演變規律,可以為研究顆粒材料的宏細觀多尺度力學特性提供新的思路.

本文將選擇具有不同非球度的橢球顆粒體系為研究對象,采用連續離散耦合分析方法進行三軸剪切數值模擬,分析不同非球度的橢球顆粒試樣在剪切過程中的宏細觀力學響應,并基于Voronoi 元胞對橢球顆粒體系的局部自由體積進行定量分析,探討局部自由體積的分布特征和演化規律以及受顆粒形狀的影響.

1 橢球顆粒體系三軸剪切數值試驗

1.1 FDEM 基本理論

FDEM 最早由Munjiza 等[20]提出,充分融合了有限元和離散元方法的優勢.顆粒的應力變形計算采用有限單元法,顆粒運動和接觸模型采用離散單元法.FDEM 中顆粒均由有限元網格構成,相比其他不連續數值模擬方法而言,最吸引人的優點是能夠考慮各種復雜形狀[33-36].

有限元網格不僅定義了顆粒的形狀和邊界,而且可以很方便進行接觸檢索以及引入接觸模型.在FDEM 中,罰函數法被用于顆粒間的接觸分析,假定接觸力偶相互侵入,根據重疊量在節點間產生分布式接觸力.切向力的最大值根據庫侖摩擦定律控制.本文采用線性接觸模型計算顆粒間的接觸力,基于兩個接觸顆粒的相對速度,通過阻尼力定律確定阻尼力.接觸力的計算公式如下

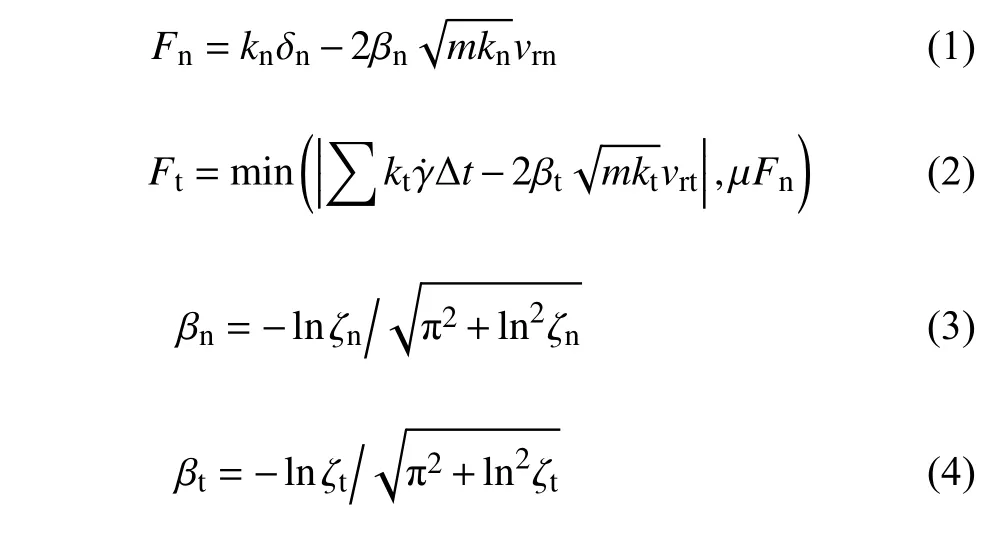
式中,和 分別為節點法向與切向接觸剛度,定義knkt為kn=pnAnode,kt=ptAnode,pn和pt分別為法向和切向罰剛度,Anode為接觸面上的節點控制區的面積,為滑移率,Δt為時間增量,δn為節點侵入量,βn和βt為法向與切向臨界阻尼系數,ζn和 ζt為法向和切向 恢復系數,m為節點質量.

1.2 顆粒形狀與數值試驗

Barrett[37]將顆粒形狀量化分為形態、圓度和表面紋理3 個層面.本文重點關注形態,故選取橢球顆粒體系作為研究對象.共生成7 種主軸長度不同的橢球顆粒,顆粒的各種形態參數如圖1 所示.其中L,I,S分別代表橢球長軸、中軸和短軸的長度.α 為Domokos系數[38],定義為α=(1/S+1/I+1/L)表征顆粒主軸各向異性,在橢球形顆粒中可以反映顆粒的非球度.ψ為球度,定義為表征顆粒形狀偏離圓球的程度,式中A和V分別代表顆粒的表面積和體積.后文分析中選取 α 作為橢球顆粒的形狀量化指標.

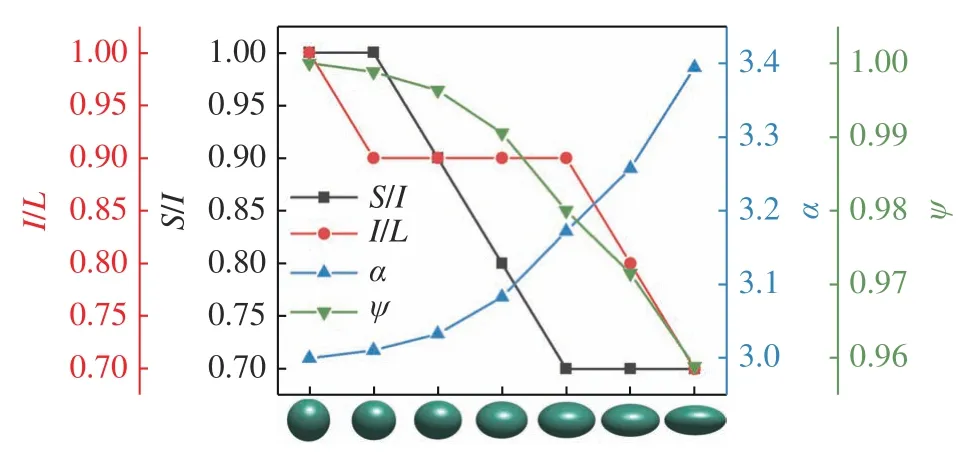
圖1 顆粒形狀描述Fig.1 Particle shape descriptors

在立方體容器中生成等效半徑(定義為等體積球體的半徑)在6.8～ 10.2 mm 范圍內均勻分布的6394 個顆粒,顆粒位置和傾向均隨機以避免產生初始各向異性.采用各向同性壓縮制樣,制樣過程中顆粒間摩擦系數設為0.1,六面無摩擦的剛性墻體緩慢壓縮試樣直至達到目標圍壓0.5 MPa.圖2 為α=3.394的數值試樣,試樣尺寸為0.42 m × 0.42 m ×0.42 m.采用常規三軸應力路徑加載,圍壓保持σ2=σ3=0.5 MPa,控制頂部和底部兩塊剛性墻體以恒定速度相向移動.

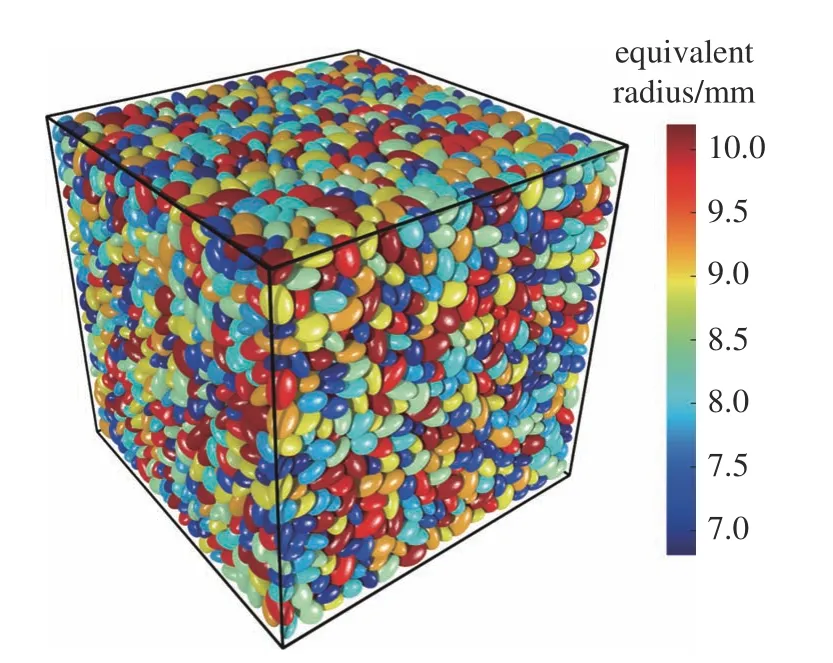
圖2 數值試樣Fig.2 Numerical sample

1.3 細觀參數率定

數值試驗的可靠度很大程度取決于參數取值.本試驗中顆粒密度、彈性模量和泊松比參考天然砂礫石的自然屬性.根據巖石材料的回彈性質[39],臨界阻尼系數取0.03,對應的恢復系數為0.9.Tatone 和Grasselli[40]驗證了當接觸罰剛度設為10 倍彈性模量時所得到的彈性響應與室內物理試驗匹配較好,故本試驗接觸罰剛度設為彈性模量的10 倍.通過顆粒柱坍塌物理試驗和數值試驗對比分析來率定顆粒摩擦系數.具體步驟如圖3 所示:選取粒徑在6～ 10 mm均勻分布的砂礫石裝入無底板圓筒,隨后緩慢抽離圓筒,重復10 次試驗,測得休止角均值為29.19°.對物理試驗中的砂礫石進行掃描,通過主成分分析得到主軸長度,在此基礎上重構出形狀相近的橢球顆粒.調整顆粒摩擦系數進行顆粒柱坍塌數值試驗,使得休止角逼近物理試驗的結果,最終摩擦系數設為0.5 時休止角為29.5°.FDEM 數值模擬所需細觀參數匯總于表1.

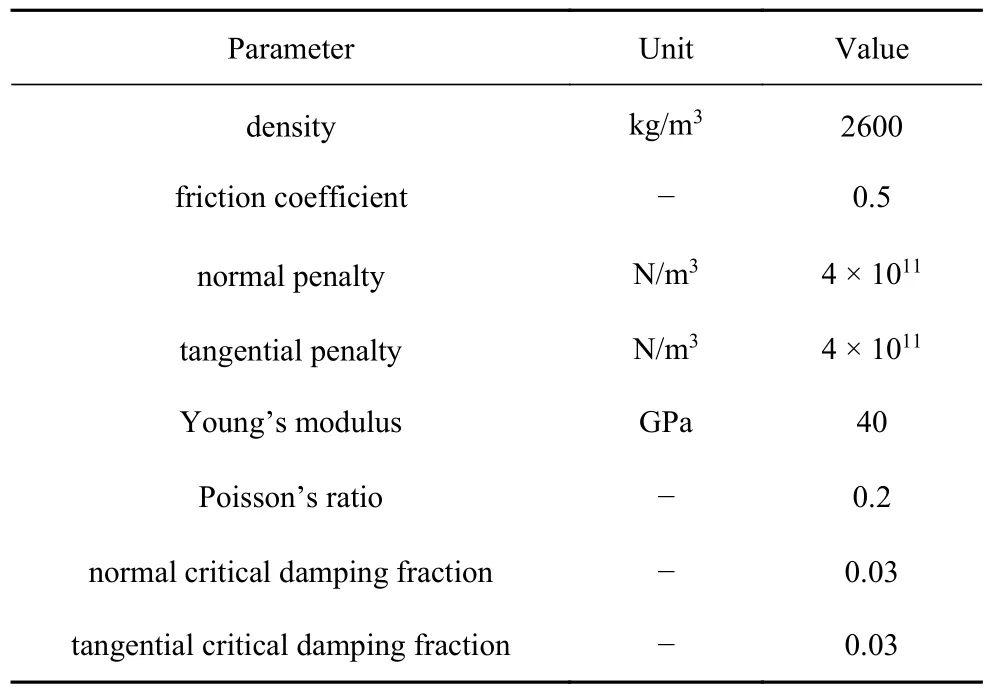
表1 FDEM 數值模擬細觀參數Table 1 Parameters used in the FDEM simulation

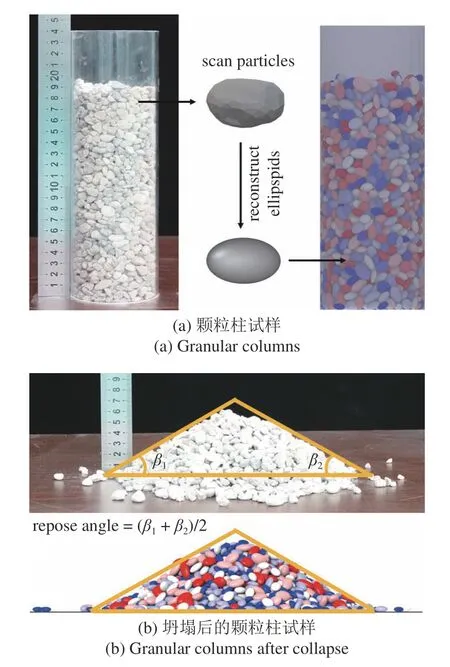
圖3 顆粒柱坍塌試驗Fig.3 Granular column collapse tests

1.4 宏觀力學響應

圖4 和圖5 分別為7 組不同非球度的橢球顆粒試樣的偏應力?軸向應變和體積應變?軸向應變關系曲線.不同試樣的宏觀響應呈現相似的規律,偏應力在加載初期迅速上升達到峰值,隨后開始下降,呈現出明顯的應變軟化現象.試樣在加載初期有少量體積壓縮,隨后發生明顯的體脹.在較大軸向應變時偏應力和體積應變都趨于穩定或呈緩慢變化趨勢.這種應力和體積響應在密實的無黏性顆粒材料中非常典型[6].隨形狀參數 α 增大,即顆粒非球度增大,試樣的剪切強度明顯增大,并伴隨著更加顯著的剪脹.目前普遍認為這種影響源自非球顆粒的互鎖效應,其增強了顆粒抵抗轉動的能力[12,41].

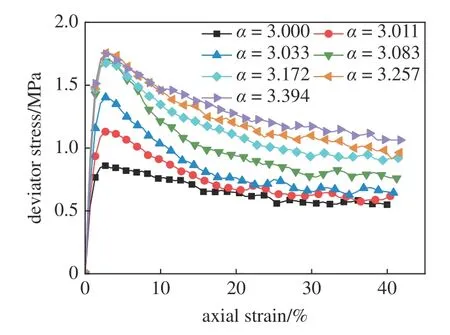
圖4 不同非球度的橢球顆粒偏應力?軸向應變Fig.4 Curves of deviatoric stress versus axial strain for ellipsoidal particles with different asphericity

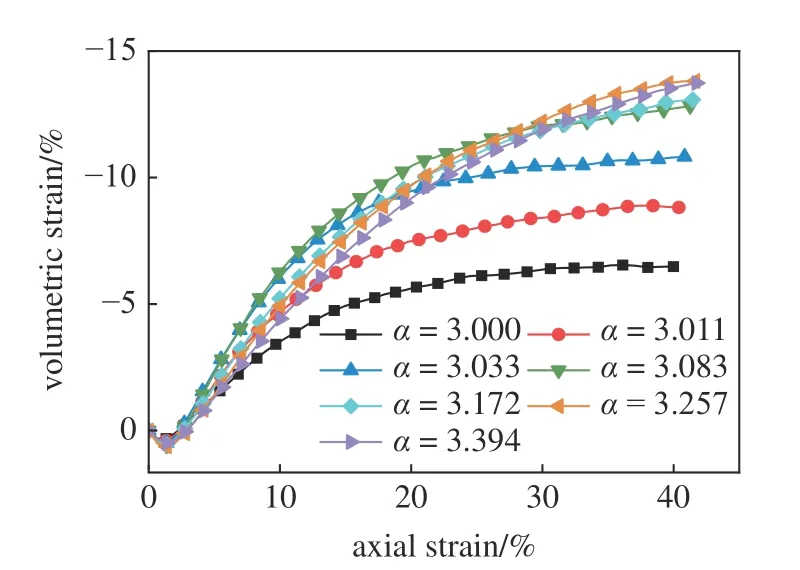
圖5 不同非球度的橢球顆粒體積應變?軸向應變Fig.5 Curves of volumetric strain versus axial strain for ellipsoidal particles with different asphericity

2 非球形顆粒的Voronoi 剖分方法

Voronoi 剖分作為一種基本幾何結構劃分方法,將離散的顆粒在空間上劃分,利用所得到的空間結構來表征材料的細觀結構,目前已成為結構表征的一種常用手段.其中圓球顆粒的Voronoi 剖分被廣泛應用,計算軟件也較為成熟(如Voro++[42]).相比而言,非球顆粒的Voronoi 剖分由于實現困難,在顆粒材料的計算分析中鮮有報道.為實現非球顆粒的Voronoi 剖分,Schaller 等[43]提出了Set Voronoi 剖分方法,現已被成功運用于非球顆粒體系的細觀結構分析[44-45].具體步驟如圖6 所示:(1)在顆粒表面均勻分布足夠多的點,得到每個顆粒表面的離散點集;(2)計算所有顆粒表面離散點的Voronoi 元胞;(3)將屬于同一顆粒的Voronoi 元胞合并,形成該顆粒的Voronoi 元胞.

圖6 Set Voronoi 剖分二維示意圖Fig.6 Two-dimensional illustration of Set Voronoi tessellation

上述步驟適用于完全分離的非球顆粒體系.然而在FDEM 中,由于顆粒間會相互侵入,會造成局部計算失準.為了避免這種情況,在進行離散點的Voronoi 剖分之前,將每個顆粒表面離散點沿其法向方向收縮一定距離,可在不影響Voronoi 剖分結果的同時避免局部誤差[43].圖7 為圓球顆粒和橢球顆粒的Voronoi 元胞示意圖,可以看出圓球的Voronoi元胞是凸多面體,而橢球的Voronoi 元胞表面會存在凹面,形態更加復雜.

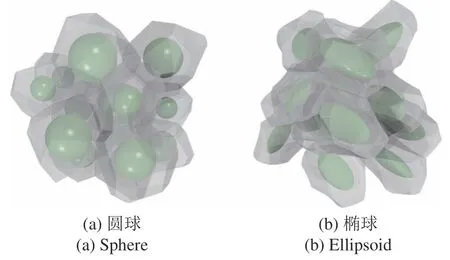
圖7 圓球和橢球顆粒的Voronoi 元胞Fig.7 Voronoi cells of spherical and ellipsoidal particles

3 Voronoi 元胞的各向異性

對于顆粒材料而言,即使是圓球顆粒體系,在剪切過程中仍然會產生各向異性[46].由于各向異性與顆粒材料的力學性質密切相關,相關研究受到廣泛關注.例如Ouadfel 和Rothenburg[24]基于組構和接觸力的各向異性張量,推導了(stress-force-fabric,SFF)關系,建立了組構各向異性、接觸力各向異性與宏觀應力比之間的關系.組構和接觸力是對接觸狀態的描述,相比而言,Voronoi 元胞是對顆粒局部空間的描述,其形狀的不規則程度可以用來量化局部空間各向異性.由于Voronoi 元胞本質上是一個多面體,在量化其形狀特性上可以借鑒于顆粒形狀的描述指標.引入最常見的球度,描述Voronoi 元胞形狀偏離圓球(各向同性)的程度,定義其為與元胞等體積球體的表面積與元胞表面積的比值

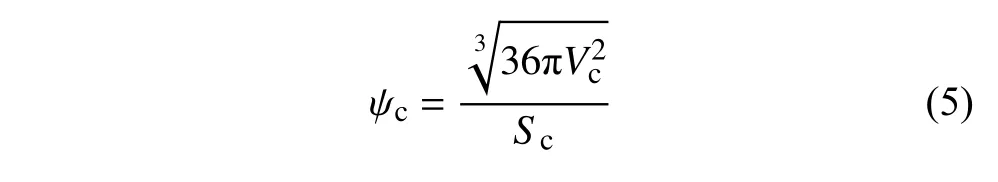
式中,Vc和Sc分別代表Voronoi 元胞的體積與表面積.

為了避免邊界效應,本文分析排除了在邊界2 倍平均粒徑范圍內的顆粒.圖8 為不同非球度的橢球顆粒試樣在不同加載階段(εa為軸向應變)的Voronoi 元胞球度 ψc的概率密度分布函數(probability density function,PDF).可以發現 ψc呈現高斯分布,圖中實線為高斯分布函數擬合曲線.在加載過程中 ψc分布逐漸向左移動(均值降低),且在加載到較大應變時趨于穩定.這說明顆粒材料在剪切過程中,局部空間的各向異性會逐漸增強直至系統達到臨界狀態,且隨顆粒非球度增大各向異性增強越明顯,這與組構各向異性和接觸力各向異性的演化類似[41,47].在剪切過程中,ψc分布的標準差也逐漸增大.

圖8 不同非球度的橢球顆粒在不同加載階段的Voronoi 元胞球度概率密度分布Fig.8 Probability density distributions of sphericity of Voronoi cells at the different loading states for ellipsoidal particles with different asphericity

當顆粒材料充分剪切后,會達到一個與初始狀態無關的力學穩定態,即臨界狀態.顆粒材料在該狀態時的力學性質受到廣泛關注[7,11].本文試樣雖未完全達到理想的臨界狀態,但是在加載后期應力狀態和體積已經趨近于穩定,故選取軸向應變40%時為試樣的“臨界狀態”,代表充分剪切后的狀態.圖9 為不同非球度的橢球顆粒試樣在臨界狀態的Voronoi元胞球度概率密度分布.隨形狀參數 α 增大 ψc分布向左平移,分布更廣.圖10 展示了臨界狀態下Voronoi元胞球度與顆粒形狀參數 α 的線性關系.這說明局部各向異性的分布強烈依賴顆粒形狀.相比圓球,橢球顆粒可以產生更為復雜的局部結構.

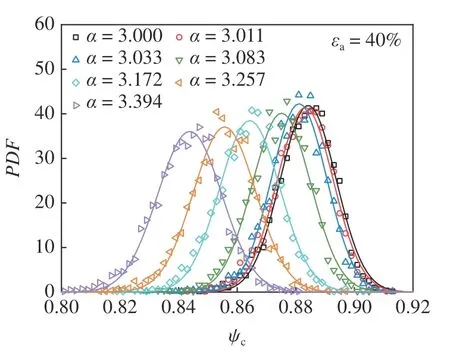
圖9 不同非球度的橢球顆粒在臨界狀態的Voronoi 元胞球度概率密度分布Fig.9 Probability density distributions of sphericity of Voronoi cells at critical state for ellipsoidal particles with different asphericity

4 局部自由體積分布及演化規律

為了量化顆粒尺度自由體積的大小,引入局部孔隙 比eloc=(Vc?Vp)/Vp,其中Vp和Vc分別為顆粒體積和其對應的Voronoi 元胞體積.圖8 展示了不同非球度的橢球顆粒試樣在剪切過程中局部孔隙比eloc的概率密度分布.局部孔隙比eloc呈現類高斯分布.針對局部自由體積的統計分布特性已有一定報道,Schaller 等[45]發現扁橢球顆粒局部體積分數1/(1+eloc)近似服從高斯分布,Dong 等[32]發現橢球顆粒和柱狀顆粒局部孔隙比服從對數正態分布,Zhao 等[30]認為局部孔隙率eloc/(1+eloc)服從一個修改的對數正態分布.此外,還有一些研究發現圓球顆粒堆積體的局部體積分數的倒數(1+eloc) 服從k?Γ 分布[48-49].上述研究中以k?Γ 分布的擬合參數最少,其函數為

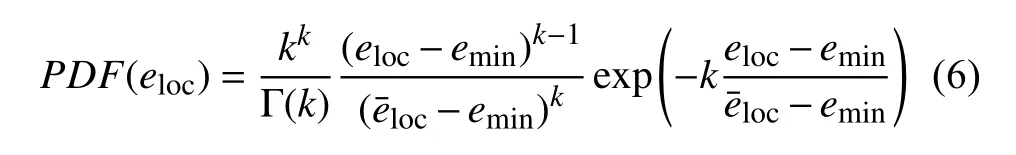
式中,k為表示分布函數形狀的參數,Γ 為伽馬函數,emin為當前堆積狀態下最小局部孔隙比,loc為局部孔隙比的均值.

圖11 中實線為k?Γ 函數擬合曲線.雖然k?Γ 分布是針對圓球顆粒體系提出的,但是對于橢球顆粒體系仍然適用.在加載過程中eloc分布逐漸向右移動,峰值減小并且分布范圍更寬,這意味著顆粒在剪切過程中局部自由體積變大且分布更廣.在加載后期這種演變逐漸趨于穩定,與試樣先剪脹后達到臨界狀態的現象相吻合.隨非球度增大這種演變越明顯,這與圖5 中剪脹隨 α 增強相對應.

圖11 不同非球度的橢球顆粒在不同加載階段的局部孔隙比概率密度分布Fig.11 Probability density distributions of local void ratio at the different loading states for ellipsoidal particles with different asphericity

圖12 為全局孔隙比eglo=0.638時不同非球度的橢球顆粒試樣的局部孔隙比的概率密度分布,此時7 組試樣剪切狀態不同,軸向應變分別為9.0%,12.7%,15.2%,21.0%,27.1%,31.8%和37.7%.可以發現不同非球度試樣的局部孔隙比分布基本一致,這說明顆粒局部孔隙比的分布僅與全局孔隙比相關,不受顆粒形態和剪切狀態的影響.圖13 為不同非球度的橢球顆粒試樣的局部孔隙比分布標準差σ(eloc) 與全局孔隙比eglo的關系.σ (eloc)與eglo呈現明顯的線性關系,且這個線性關系不受顆粒形態影響,進一步證明了顆粒局部孔隙比的分布僅受全局孔隙比控制.

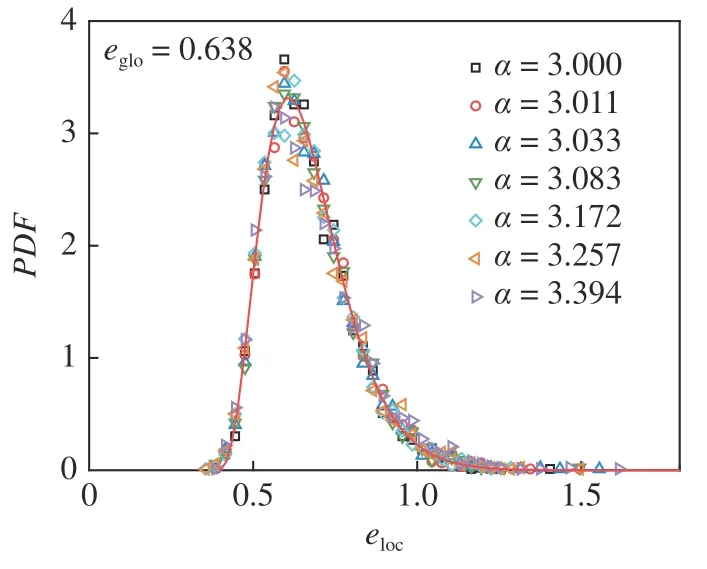
圖12 不同非球度的橢球顆粒在全局孔隙比相同時局部孔隙比概率密度分布Fig.12 Probability density distributions of local void ratio at the states as same global void ratio for ellipsoidal particles with different asphericity

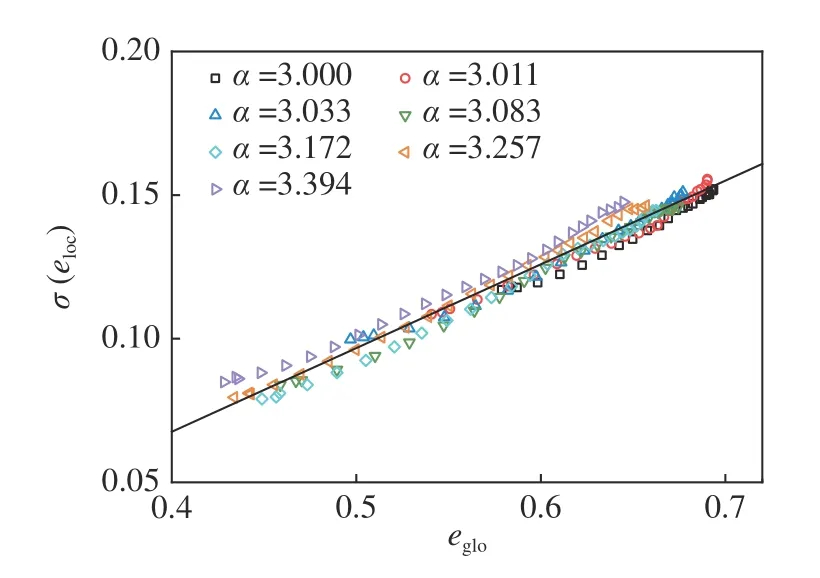
圖13 局部孔隙比的標準差與全局孔隙比的關系Fig.13 Relationship between standard deviation of local void ratio and global void ratio

從局部孔隙比分布的演化可知剪切過程中局部自由體積的變化是非均勻的,探索局部孔隙比波動可以幫助了解顆粒體系剪脹的細觀機理.選取了5 個加載階段(εa=4%,10%,20%,30%和40%),分析不同非球度的橢球顆粒試樣在應變窗口 Δ εa≈0.8%的局部孔隙比波動.圖14 為不同非球度的橢球顆粒試樣在不同加載階段的局部孔隙比波動的概率密度分布.局部孔隙比的波動呈現非對稱拉普拉斯分布(asymmetric laplace distribution,ALD),其函數為

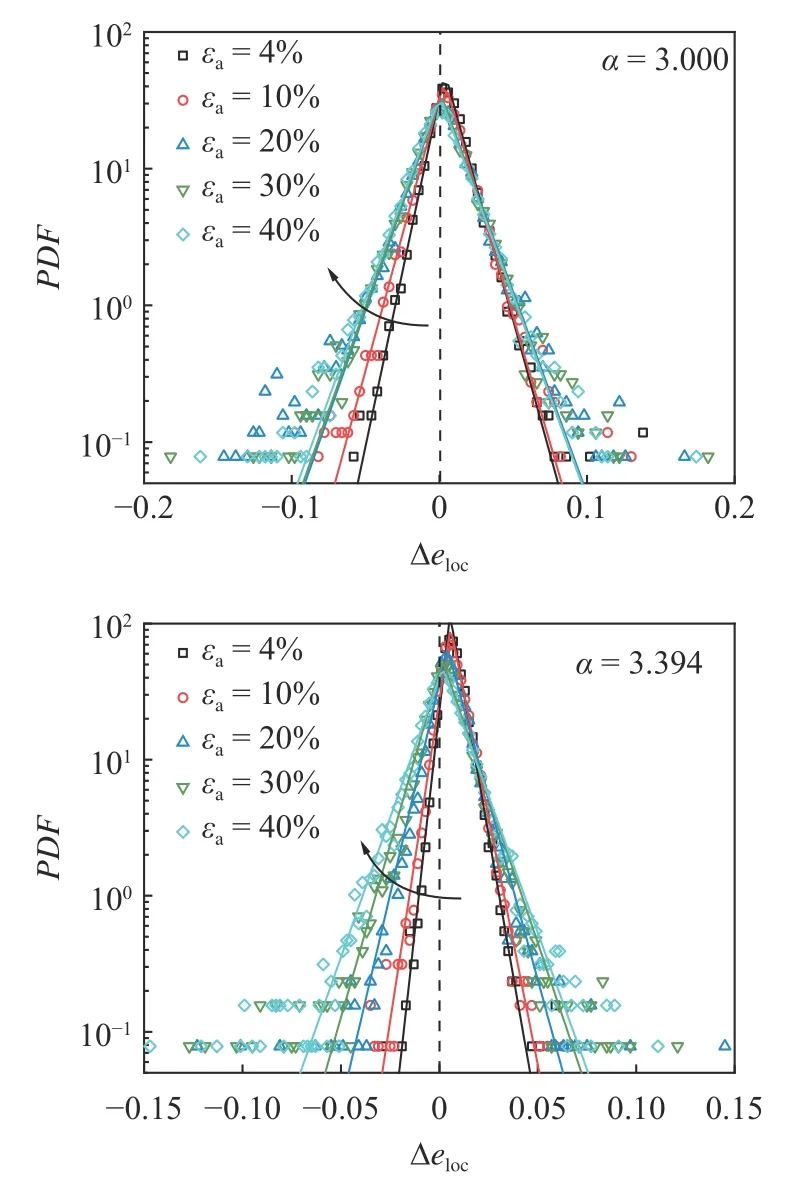
圖14 不同非球度的橢球顆粒試樣在不同加載階段的局部孔隙比波動概率密度分布Fig.14 Probability density distributions of local void ratio fluctuations at the different loading states for particles with different shapes

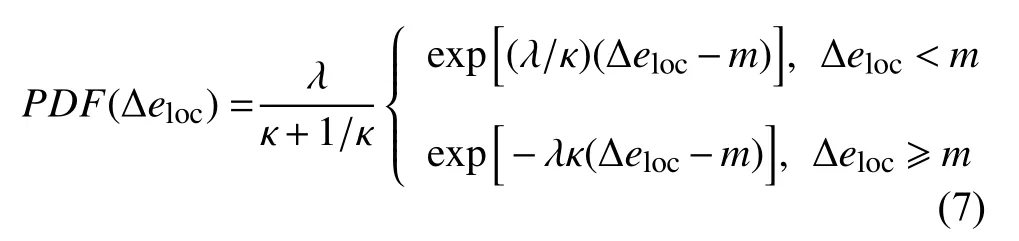
式中,m為分界點,λ 為尺度參數,κ 為非對稱參數.

Δeloc的分布可以分為左右兩個非對稱的指數函數(在單對數坐標系下表現為斜率不一致的兩段線性分布),分界點在 Δeloc=0附近.左右兩側分布的非對稱性刻畫了局部自由體積收縮和膨脹的博弈.在加載初期(εa=4%)體積膨脹明顯處于優勢地位(圖中圖14(a)斜率絕對值小于圖14(b)),試樣表現出明顯的剪脹行為.隨形狀參數 α 增大,兩側斜率差異增大,這意味著有更顯著的體積膨脹,與宏觀體積響應相符合(圖5).隨著剪切進行,代表體積膨脹的圖14(a)體積波動分布變化較小,而圖14(b)分布的斜率有明顯下降,兩側趨于對稱,即剪脹會隨剪切過程逐漸停止.

ALD 中非對稱參數 κ 為分布兩側斜率比值的平方,描述了ALD 的非對稱程度,也刻畫了體積膨脹的強度.κ 越小體積膨脹越明顯,κ=1時體積無變化.如圖15 所示,κ 與全局孔隙比eglo呈現明顯的線性關系,并在 κ=1附近截斷.這意味著體積膨脹的強度很大程度上取決于試樣當前全局孔隙與臨界全局孔隙比的差值,故隨 α 增大體脹更顯著可以歸因于橢球顆粒在相同固結條件下可以形成更密實的堆積.

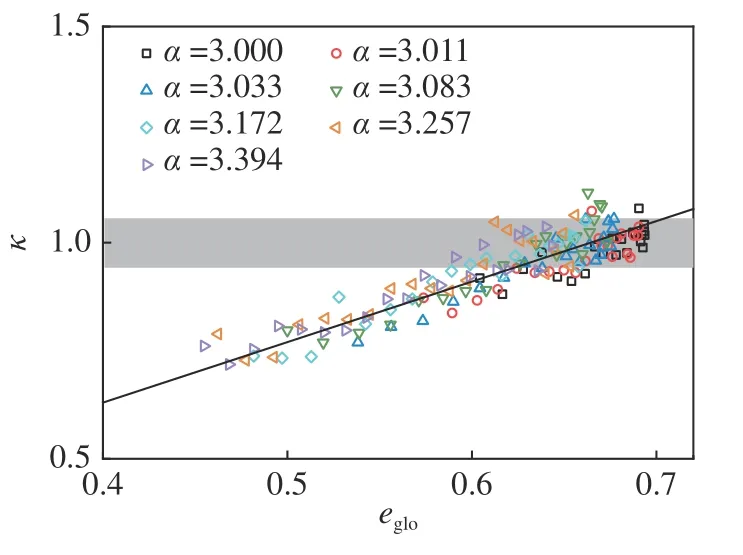
圖15 非對稱參數 κ 與全局孔隙比的關系Fig.15 Relationship between asymmetric parameter κ and global void ratio

5 結論

本文采用連續離散耦合分析方法,對具有不同非球度的橢球顆粒試樣進行了三軸剪切數值模擬.基于Set Voronoi 剖分技術對剪切過程中的顆粒試樣進行Voronoi 元胞分割,研究了顆粒試樣在剪切過程中局部自由體積的統計分布特性和演化規律,以及顆粒形態的影響.主要結論如下:

(1)不同橢球顆粒試樣的Voronoi 元胞的球度在剪切過程中均服從高斯分布,但其均值降低,標準差略有上升,表明顆粒材料在剪切過程局部各向異性的逐漸增強.局部各向異性程度與顆粒形態顯著相關,臨界狀態時Voronoi 元胞球度隨顆粒形態參數 α線性減小.

(2) 不同橢球顆粒試樣的局部孔隙比均服從k?Γ 分布,且這個分布僅與全局孔隙比相關,不受顆粒形態和剪切狀態的影響.非球度更大的顆粒在剪切過程中會產生更強烈的重排列,導致局部孔隙比和Voronoi 元胞球度在剪切過程中的變化隨顆粒形狀參數 α 的增大而增大.

(3)不同非球度的橢球顆粒試樣的局部孔隙比波動均服從非對稱拉普拉斯分布,這種不對稱性刻畫了局部自由體積收縮和膨脹的博弈.非對稱參數與全局孔隙比呈現明顯的線性關系,表明體積膨脹的強度很大程度上取決于試樣當前全局孔隙此與臨界全局孔隙比的差值.