丘陵山地果園智能運輸小車減振結構優化設計*

戚得眾，郭林，阮曉松，閆行行

(1. 湖北工業大學,武漢市，430068； 2. 湖北省農業機械工程研究設計院，武漢市，430068)

0 引言

傳統丘陵山地果園大多是采用人力的方式來運輸果品，由于農村勞動力的缺失，勞動力的價格不斷增高，山地智能運輸車應運而生，對降低果園運輸成本具有重要意義，但目前山地智能運輸車存在減振性能差，果品損傷嚴重等問題。要想改變現狀，需對丘陵山地智能減振小車的減振系統進行優化。

運輸小車減振系統一般為被動減振，被動減振研究主要從兩方面進行，一方面對減振結構進行研究，徐新喜等[1]對履帶式衛生急救車的振動控制進行了研究，發現兩級減振較單級減振，減振效果有很大的提高。Shen等[2]提出一種ISD懸架結構，該結構能夠在一定程度上提高懸架的性能。李小彭等[3]對傳統的單級ISD懸架系統進行改進，設計出一種雙級ISD懸架系統，該系統具有更好的低頻減振性能。另一方面對減振系統的控制進行研究，遲媛等提出一種適用于輪式拖拉機的主動懸架減振系統，該主動懸架系統較傳統被動懸架系統減振效果提高27%。滕緋虎[4]提出一種適用于履帶裝甲車的半主動懸掛系統并進行仿真，仿真結果表明半主動懸掛減振性能優于全扭桿懸掛和裝有減振器的扭桿懸掛。

諸多學者對履帶車輛及農用車輛減振進行相應研究[5-13]，取得不錯成果，但沒有針對丘陵山地履帶運輸車進行減振研究。為提高丘陵山地履帶運輸車的性能，對其減振性能研究迫在眉睫。首先進行理論分析，設計出一種適用于丘陵山地果園運輸車的二級減振結構，進行減振性能仿真分析，確定山地智能運輸小車的減振結構。

1 模型構建

1.1 丘陵山地果園路面構建

路面性能可以通過路面不平度來進行評價，當車速穩定時，路面不平度符合高斯概率分布，且具有零均值的平穩均態特性，可通過功率譜密度(PSD)來描述。國標GBT 7031—2005對其有明確的規定，具體如表1所示。

對于已知路面等級的道路可以通過諧波疊加法和白噪聲法兩種不同的方法去生成路面時域不平度，可采用基于功率譜密度的諧波疊加法，利用MATLAB編程生成路面時域不平度。

南京農業機械化研究所的徐竹鳳等對果園不平度進行了研究，最后通過測量得出了丘陵山地果園的路面等級在C級到D級之間。針對山地智能運輸小車的使用場景，以北方的蘋果園為例，選擇C級路面。當小車以1 m/s的速度行駛在C級路面，MATLAB生成路面不平度如圖1所示。

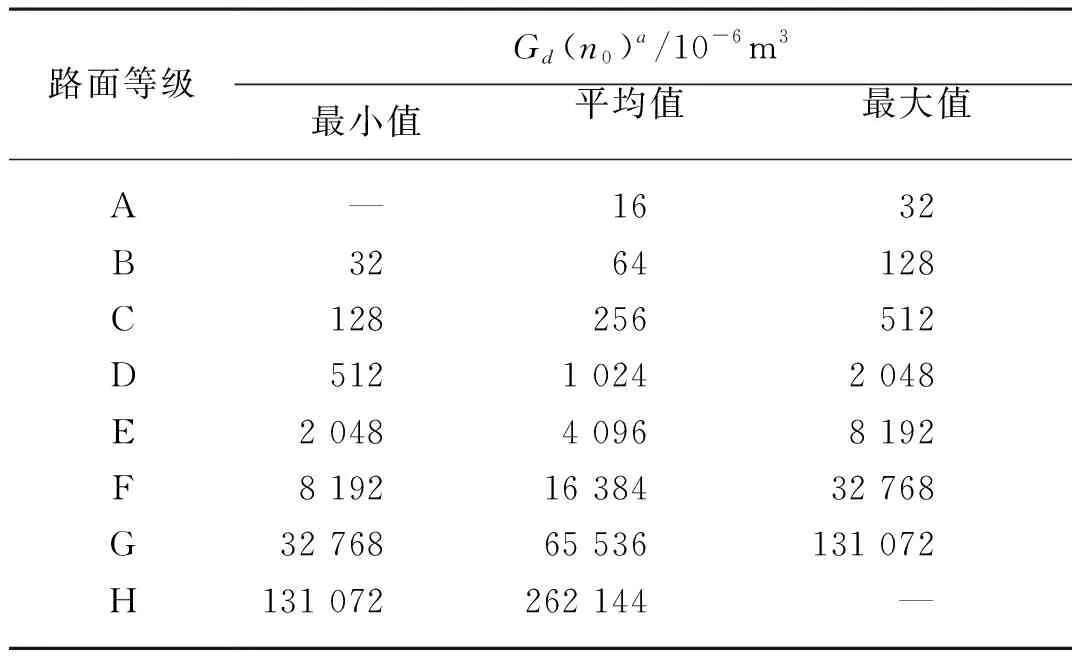
表1 路面不平度分級標準Tab. 1 Grading standards for road roughness

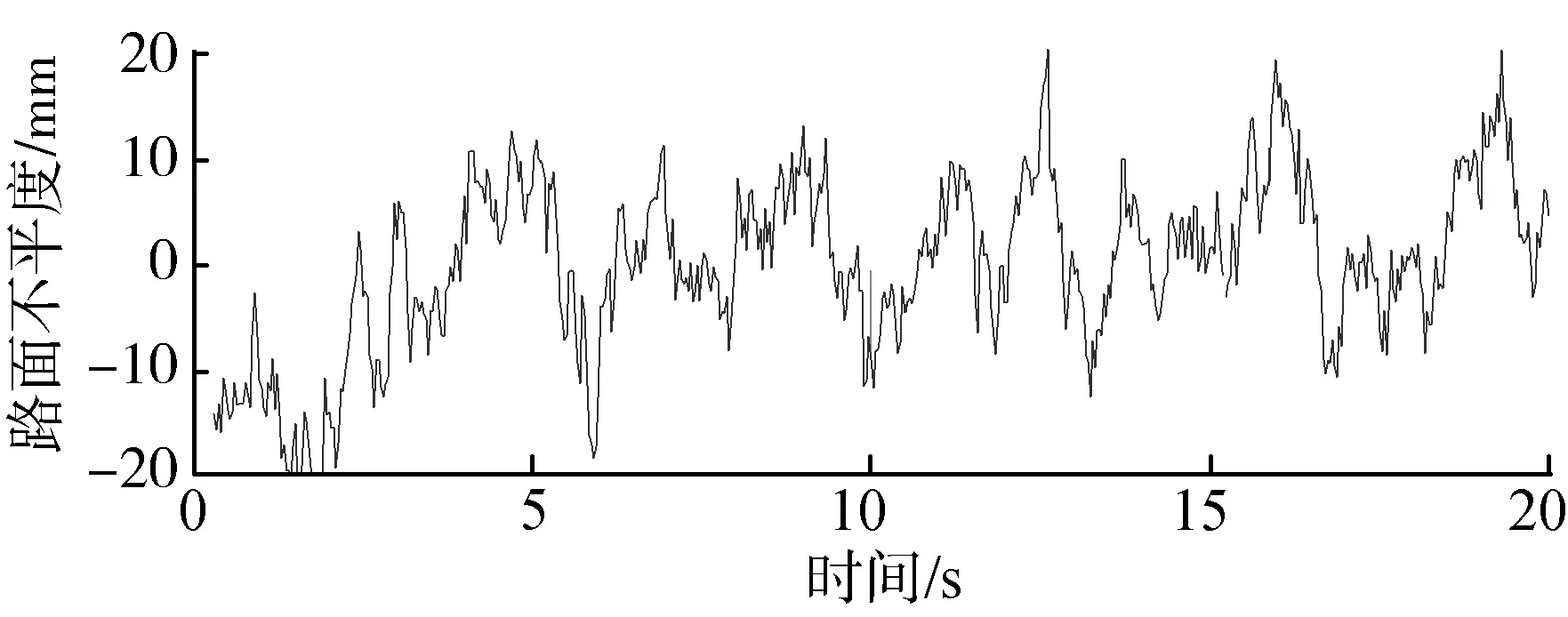
圖1 丘陵山區果園路面不平度Fig. 1 Road roughness of orchards in hilly andmountainous areas

1.2 減振系統模型構建

在車輛行駛過程中由于路況的變化，車輪會與路面產生碰撞，從而產生振動。假設車輛以勻速在的道路上行駛，當遇到路面突起時，車輪與突起部分產生碰撞，如圖2所示。忽略碰撞時的能量損失，由動量守恒定律有

MV1=MV2

(1)

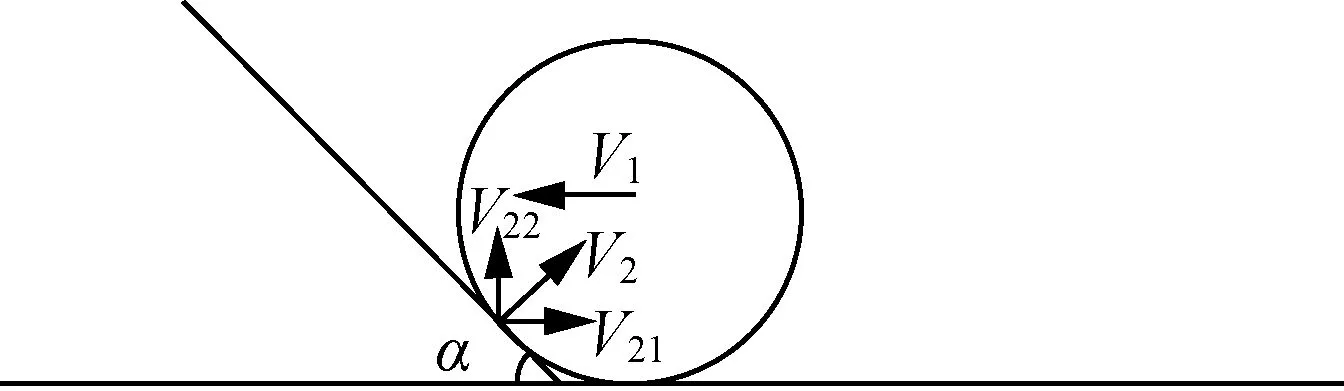
圖2 車輪路障碰撞示意圖Fig. 2 Wheel barricade collision diagram

M為車輛總質量，V1為碰撞前車輛的速度，V2為碰撞后車輛的速度。其中V1和V2的大小相等但方向不同。

設α為碰撞接觸點所在平面與道路水平面間的夾角

(2)

(3)

V21的方向與V1的方向相反，V22的方向與V1的方向垂直，V21的大小與α的大小成正比，V22的大小與α的大小成反比。F21和F22分別為車輛在V21、V22方向的受力。α取值范圍為0°～90°，丘陵地區一般不超過25°，車輛丘陵地區行駛于路面發生碰撞時會受到F21和F22兩個不同方向的力，且這兩個力存在一定的比例關系，在設計減振結構時也應同時考慮。

傳統單自由度的智能運輸小車懸架模型如圖3(a)所示，忽略支重輪的重量和剛度，懸架的剛度與阻尼為定值。圖中m為車身質量，由車架和果箱組成，k1代表懸架剛度，c1代表懸架的阻尼，z1代表在路面激勵下車身位移，q代表路面不平度函數。

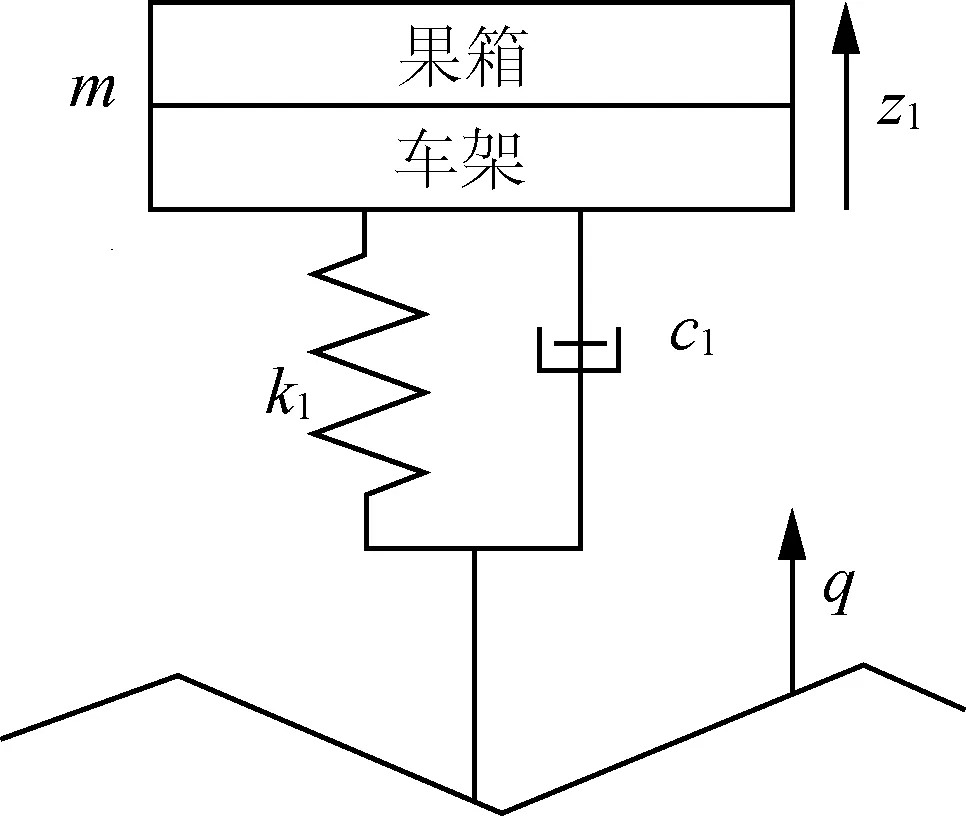
(a) 單自由度懸架

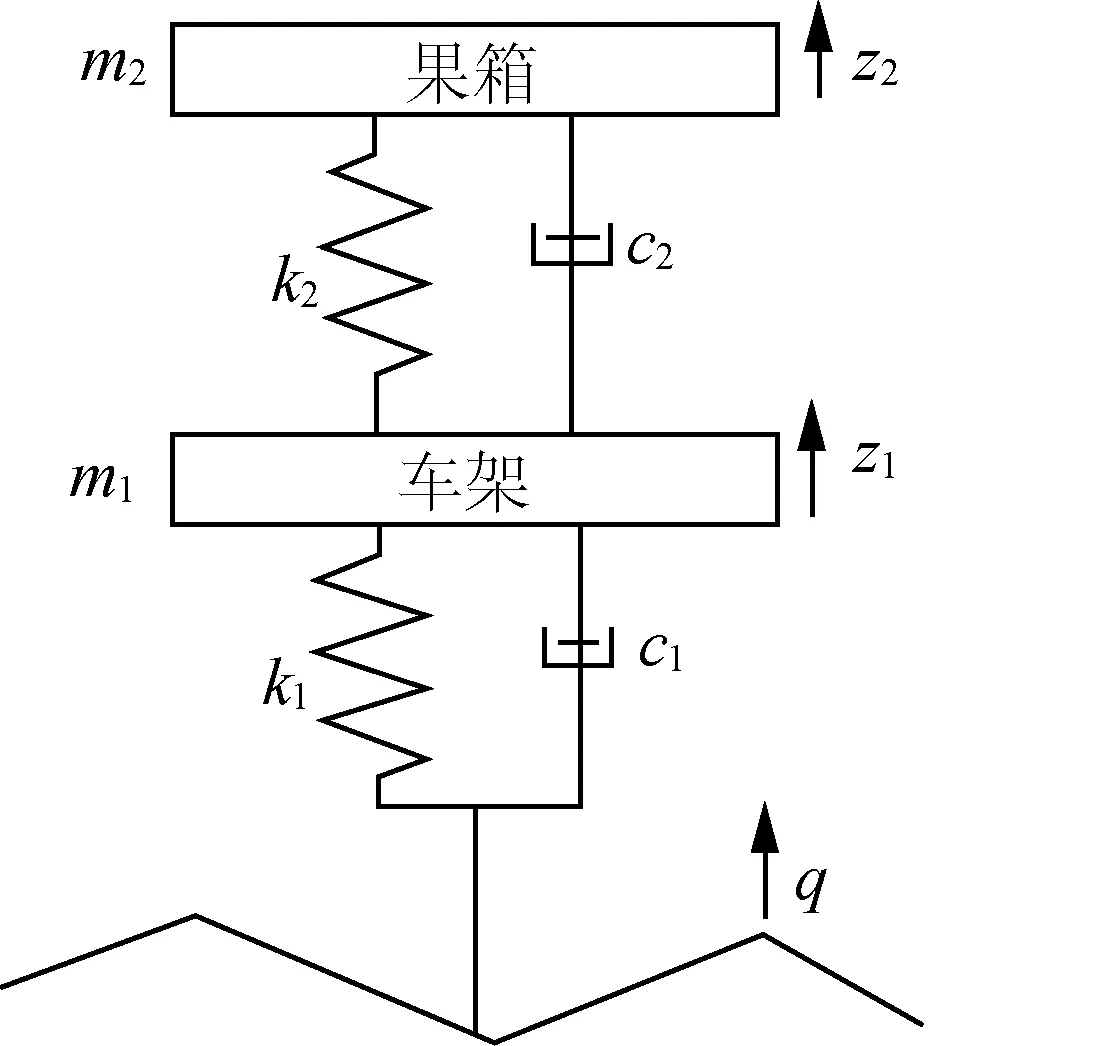
(b) 二自由度懸架圖3 懸架模型圖Fig. 3 Suspension model drawing

忽略車輪變型，車輪位移等于路面不平度，圖3(a)所示懸架系統的運動微分方程

(4)

懸架系統的激勵路面不平度函數q隨時間變化且無規律，為非周期性函數。可以將q看成一系列脈沖的作用，分別求出系統對每個脈沖激勵的響應，將它們疊加起來，就得到系統對路面不平度激勵的響應。系統對脈沖激勵的響應可以反應系統的振動特性。

系統對0時刻單位脈沖激勵下的響應

(5)

其中：

令系統達到最大超調量Mp(第一次到達極值點)的時間為tp，有

(6)

tp的大小決定懸架系統響應的變化速度，從而決定了車身的受力大小。對于剛性連接系統來說，系統達到Mp的時間與脈沖的寬度dτ相同，在非極端情況下tp大于dτ。懸架系統對脈沖激勵具有一定的減緩作用，可以將變化急劇信號轉化為平緩信號。

2 減振系統設計優化

可通過對懸架系統的結構和參數進行優化來增大tp以達到提高減振性能的目的。

2.1 結構優化設計

對減振結構進行優化，智能運輸小車的簧上部分由車架和果箱組成，路面的激勵通過懸架傳遞到車架，車架再將激勵傳遞給果箱，在單自由度懸架模型中車架和果箱間是剛性連接，果箱的加速度響應與車架的加速度響應相同。針對智能運輸小車提出一種新的減振結構，將車架和果箱間的剛性連接改為柔性連接，即在車架和果箱間添加相應的減振結構，采用兩級減振。

二自由度的智能運輸小車懸架模型如圖3(b)所示，忽略支重輪的重量和剛度，m1、m2分別代表車架質量和果箱質量，k1、c1分別代表車架與車輪間減振結構的剛度和阻尼，k2、c2分別代表車架與果箱間減振結構的剛度與阻尼，z1、z2分別代表再路面不平度激勵下車架和果箱的位移。圖3(b)所示懸架系統的運動微分方程

(7)

借助MATLAB/Simulink模塊對方程進行求解，Simulink模型如圖4所示。

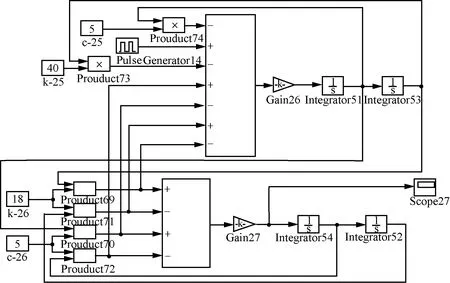
圖4 Simulink模型圖Fig. 4 Simulink model diagram

以脈沖信號作為激勵，單級減振懸架系統與兩級減振懸架系統的果箱幅值響應如圖5所示。

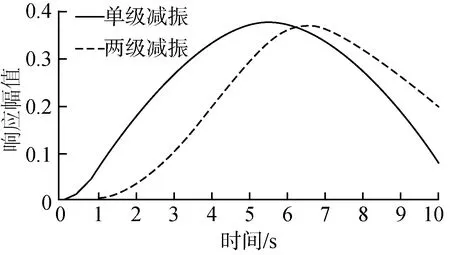
圖5 不同減振結構果箱幅值響應圖Fig. 5 Amplitude response of fruit box withdifferent vibration damping structures

圖5中兩級減振懸架系統果箱的tp大于單級減振懸架系統果箱的tp，tp越大果箱幅值響應變化速度越小，加速度越小，果箱內果品受力越小，即在脈沖激勵下二級減振系統的果品損傷率小于一級減振系統的果品損傷率。

傳統履帶車輛多采用扭桿懸架進行減振，扭桿懸架可以等效為Z向、X向的兩根彈簧減振器組合而成，可以同時對Z向和X向的激勵進行減振。扭桿懸架具有結構簡單、占用車體空間小、彈性和可靠性好等優點，選擇扭桿彈簧作為一級減振結構元器件。二級減振結構參考汽車座椅減振系統進行設計，適用于丘陵山地果園智能運輸車二自由度減振結構如圖6所示。

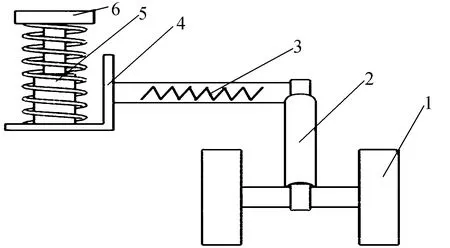
圖6 運輸車二級減振結構示意圖Fig. 6 Diagram of secondary vibration dampingstructure of transport vehicle1.支重輪 2.平衡肘 3.扭桿彈簧 4.車架5.彈簧減震器 6.果箱

2.2 結構參數優化設計

以果箱加速度響應幅值為衡量指標對二自由度系統的二級減振結構參數進行分析，令

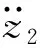
(a) 加速度響應與剛度關系圖

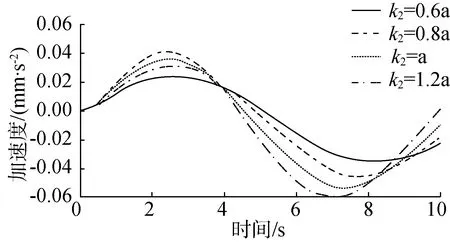
(b) 加速度響應與質量比關系圖

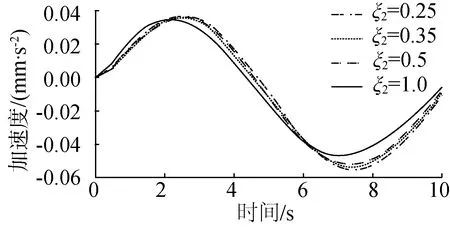
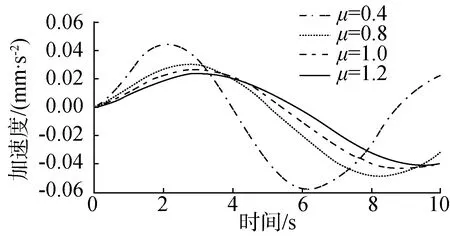
(c) 加速度響應與阻尼關系圖圖7 零初始條件下懸架系統在脈沖激勵下響應圖Fig. 7 Response diagram of suspension system under impulse excitation under zero initial condition

3 仿真分析

3.1 動力學模型構建

采用ADAMS/ATV模塊進行多體動力學仿真分析。半車動力學模型如圖8所示，相關參數如表2所示。

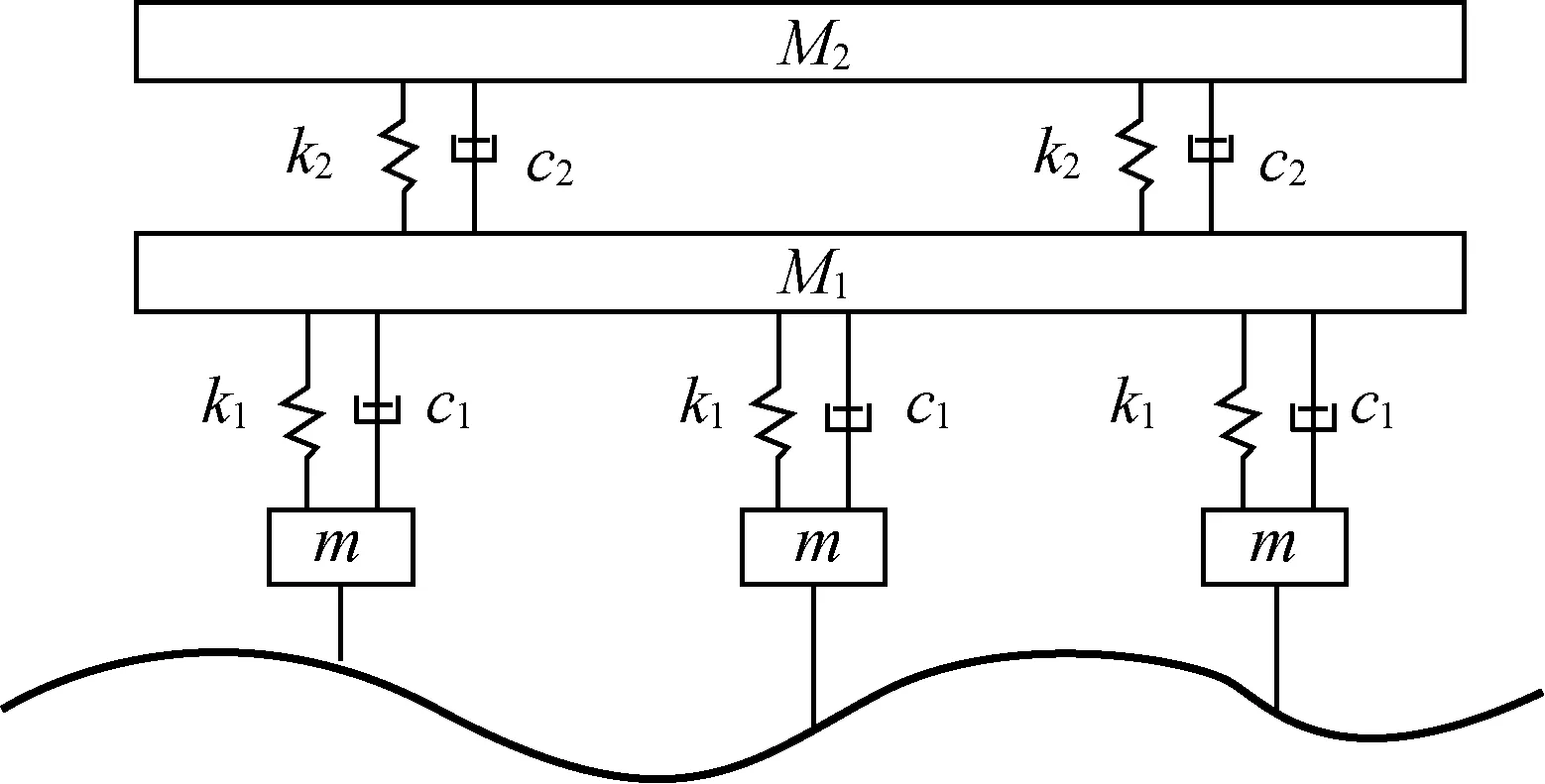
圖8 運輸車半車動力學模型Fig. 8 Dynamics model of transport vehicle and half vehicle

表2 運輸車相關參數值Tab. 2 Relevant parameter value of transport vehicle

3.2 結構優化前后仿真結果及分析

對三種不同的減振結構進行仿真分析，其中結構a和結構b分別采用扭桿懸架和非獨立式懸架，均為單級減振結構，結構c采用二級減振懸架。

山地智能運輸小車采用三種減振結構以1 m/s的速度，在構建的c級路面上行駛20 s，果箱X向的加速度和Z向的加速度響應如圖9所示。其中結構a與結構c在X向減振結構相同，仿真結果中X向加速度基本一致，因此圖9中無結構a在X向加速度響應圖。

對山地智能運輸小車在不同減振結構下X向的加速度進行分析，數據如表3所示。

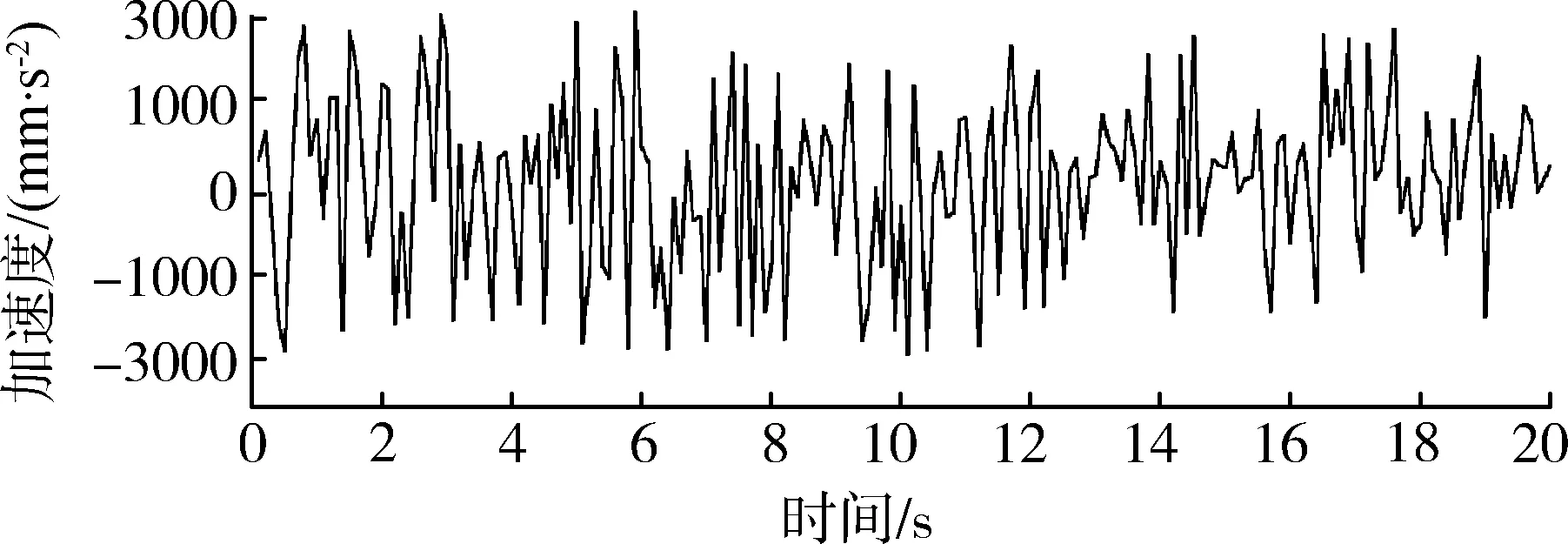
(a) 采用結構a在Z方向加速度響應圖

(b) 采用結構b在X方向加速度響應圖

(c) 采用結構b在Z方向加速度響應圖

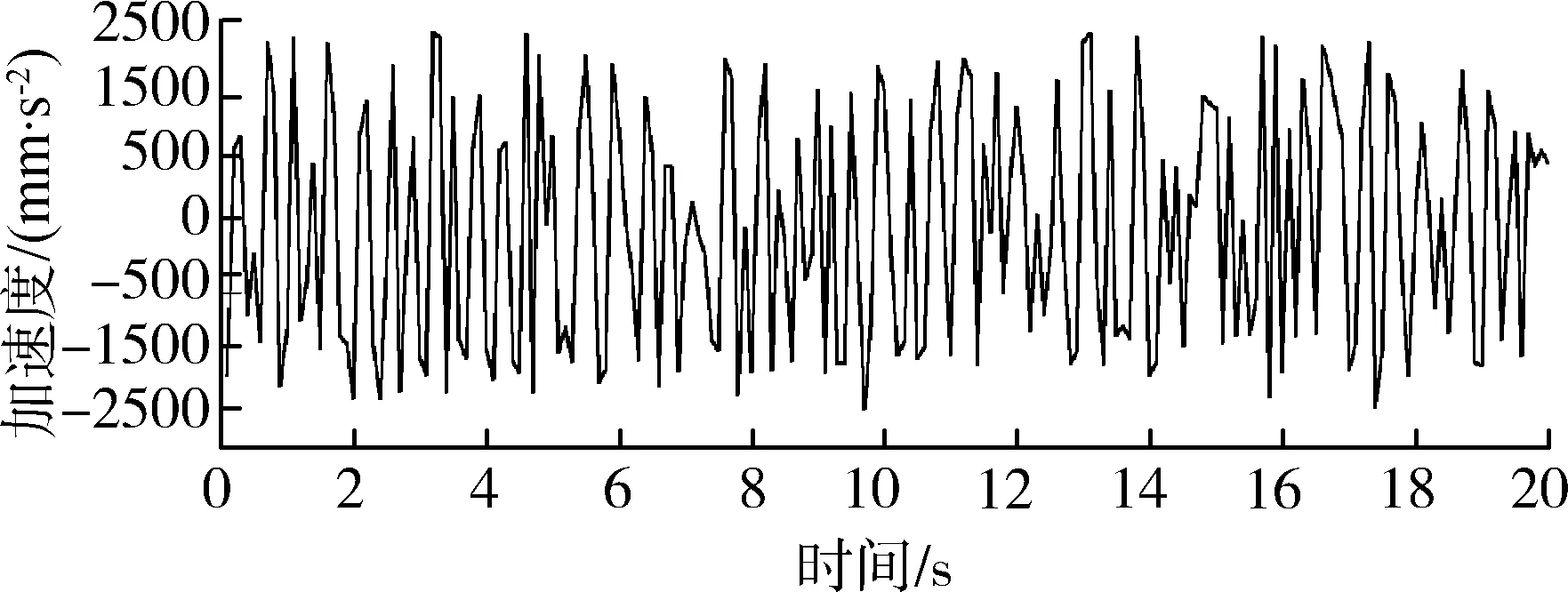
(d) 采用結構c在X方向加速度響應圖

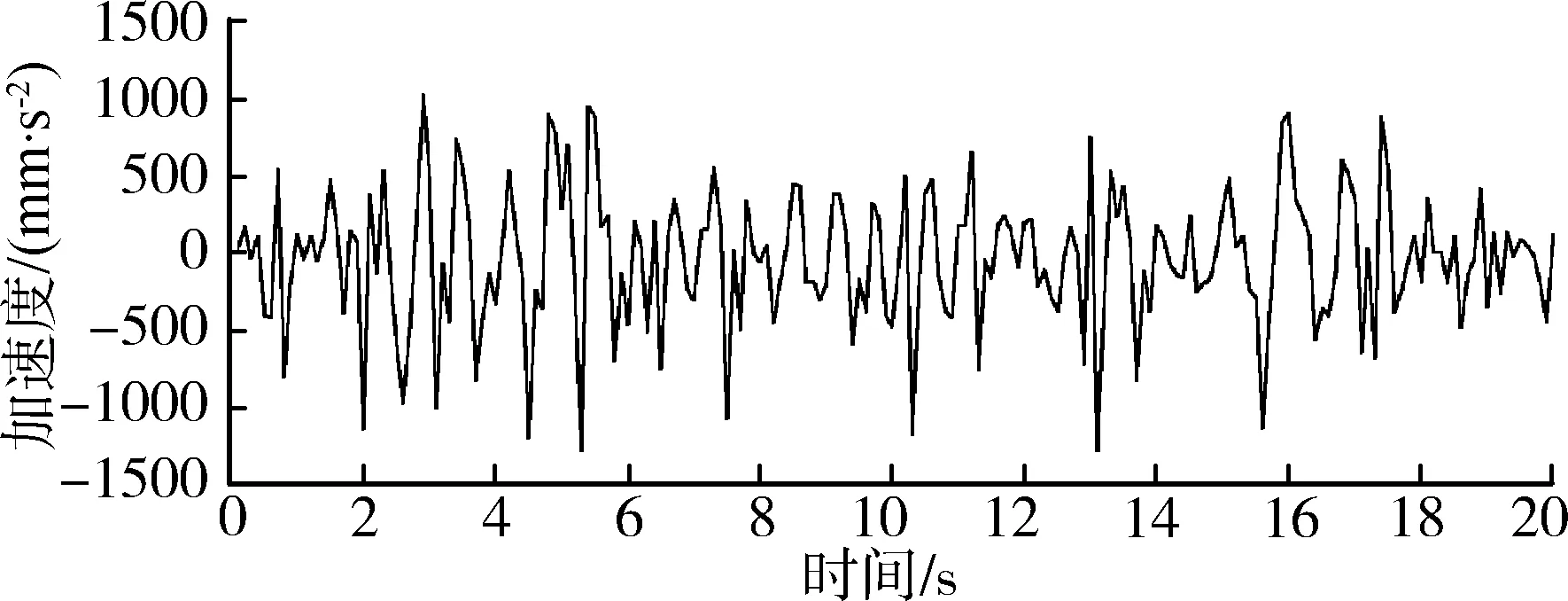
(e) 采用結構c在Z方向加速度響應圖圖9 不同結構加速度響應圖Fig. 9 Acceleration response diagram ofdifferent structures

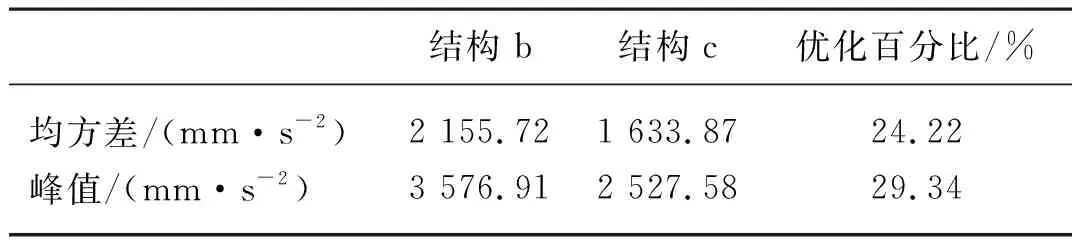
表3 X向數據對比Tab. 3 X direction data comparison

結構a與結構c都采用了扭桿懸架，扭桿懸架可以等效為X向和Z向彈簧減振器的組合，在X向具有一定的減振性能，而結構b在X向沒有任何減振措施，因此結構c與結構a在X向較結構b減振效果更好，減振性能優化24.22%。

對山地智能運輸小車采用不同減振結構下Z向的加速度進行分析，結構a、結構b與結構c的Z向加速度的峰值和均方差如圖10所示，優化效果如表4所示。

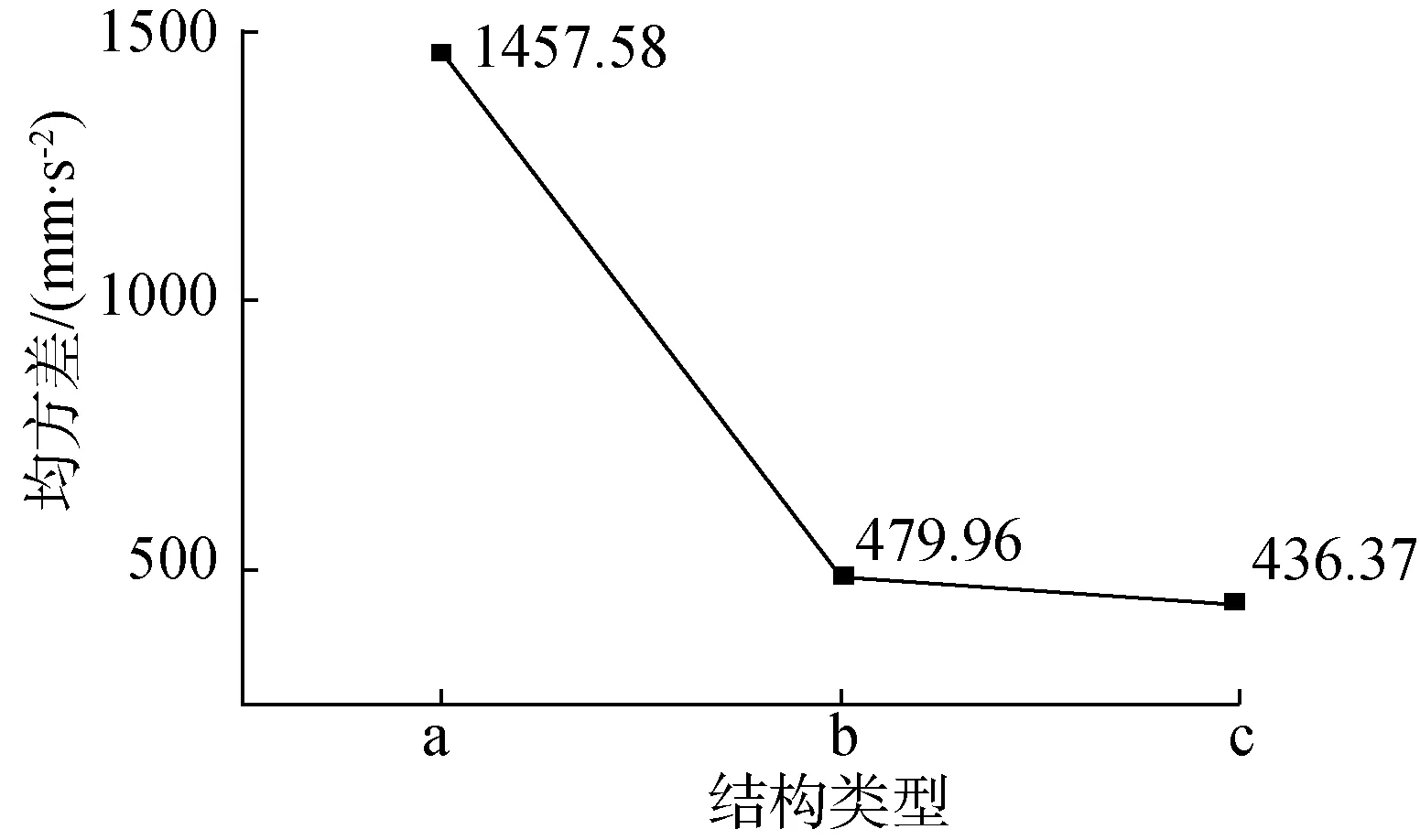
(a) Z向加速度均方差

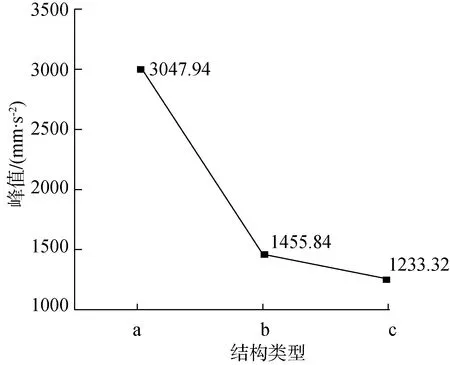
(b) Z向加速度峰值圖10 Z向優化效果對比圖Fig. 10 Z direction optimization effect comparison diagram

表4 Z向加速度響應數據對比Tab. 4 Z direction acceleration response data comparison

結構c相較于結構a，峰值優化了82.18%、均方差優化了76.75%；相較于結構b，峰值優化了24.89%、均方差優化了9.08%。結構a在Z向減振性能由扭桿懸架提供，單向減振性能一般；結構c采用兩級減振較結構a和結構b的單級減振可在一定程度上增大tp，使果箱運動更加平緩。

3.3 不同參數仿真結果及分析

對結構c的k2、μ和ξ2三個參數進行優化，由2.2節可知，適當增大μ和ξ2，適當減小k2均可提高運輸車的減振性能，μ和ξ2的值受M1和c2的影響，最終確定對k2、M1和c2進行優化，優化前后參數如表5所示。

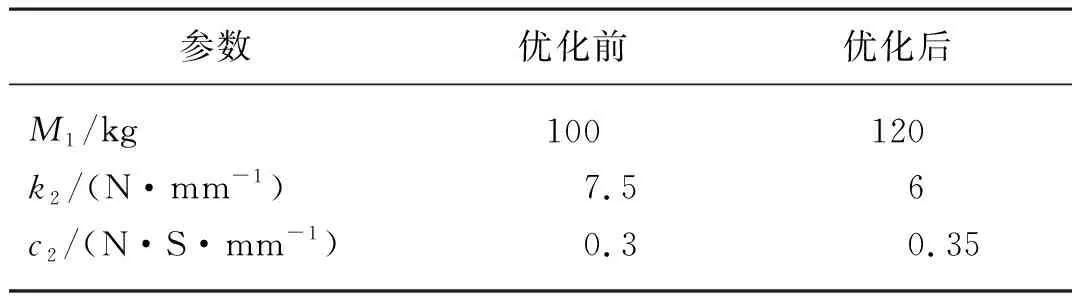
表5 優化前后參數Tab. 5 Parameters before and after optimization

優化后的結構c仿真結果如圖11所示。此次優化是針對Z向減振進行一定的優化，故只對Z向的仿真結果進行分析對比。

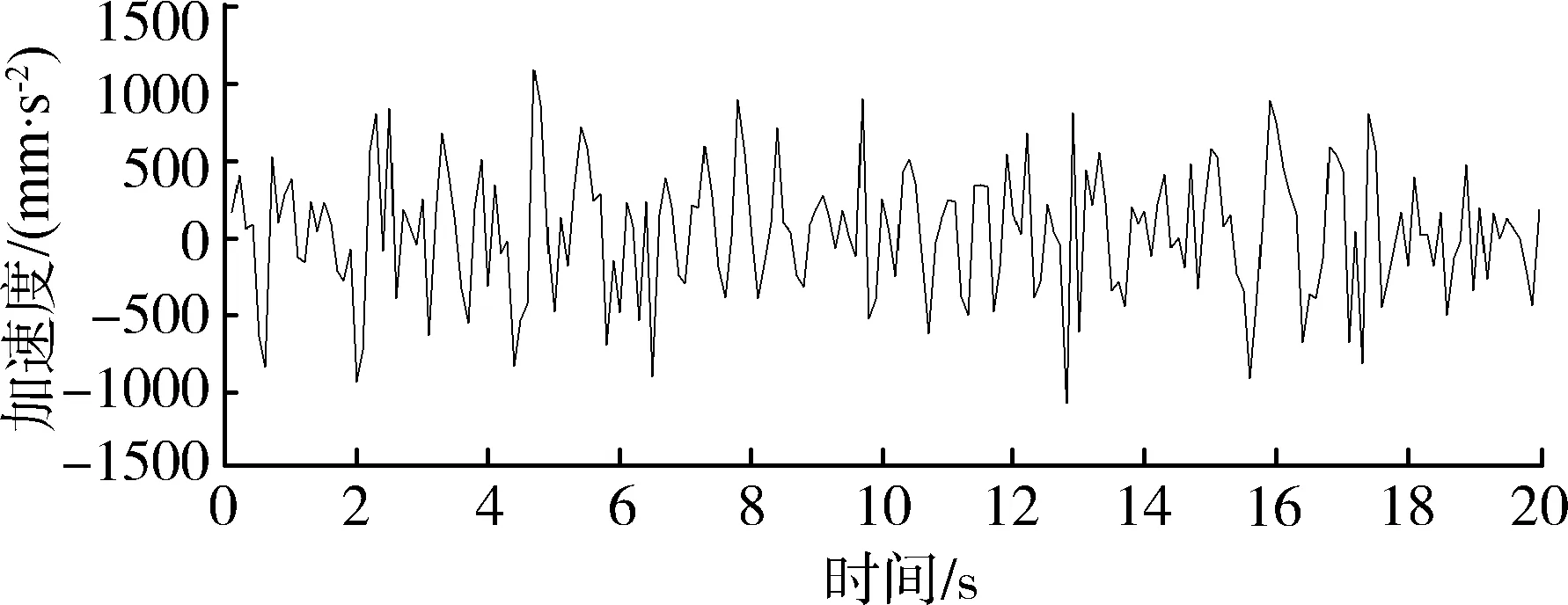
圖11 優化后果箱Z向加速度響應圖Fig. 11 Optimized consequence box Z-directionalacceleration response diagram

優化前后Z向仿真結果均方差對比如下表6所示。

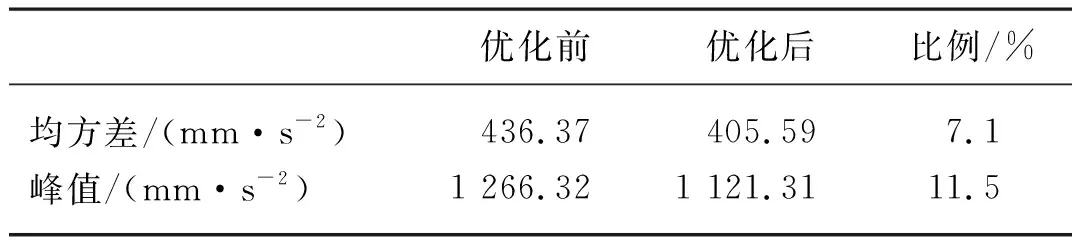
表6 Z向優化前后數據對比Tab. 6 Comparison of data before andafter Z-directional optimization

優化后的Z向加速度均方差和峰值分別較優化前提高了7.1%和11.5%，對結構c的k2、μ和ξ1三個參數進行優化可以有效的增大tp，使果箱在受到路面激勵后運動更加平緩，果箱內果實受力更小，以減小果實損傷。

通過ADAMS動力學仿真可得出結論：在Z向加速度均方差和峰值及X向加速度均方差和峰值4個方面，兩級減振懸架性能均優于或等于單級減振懸架；在適當減小k2及增大μ和ξ1后的懸架性能優于原懸架性能，具有良好的穩定性。

4 結論

1) 構建丘陵山地果園的路面模型，并對山地智能運輸小車的減振結構進行理論分析，設計出一種適用于丘陵山地履帶運輸小車的兩級減振懸架。

2) 通過Adams動力學仿真具體分析了采用不同減振結構的運輸車在c級路面以1 m/s的速度行駛時的減振性能，仿真結果表明二級減振懸架在X向和Z向都具有良好的減振效果，對比單級減振懸架Z向和X向減振性能分別優化9.08%和24.22%。

3) 以二級減振懸架為基礎，進一步優化了山地智能運輸車的減振結構的相關參數，參數優化后的懸架減振效果較優化前提高7.1%，后續研究將會做進一步改進。研究結果證明了該減振結構的正確性和合理性，能夠有效的改善智能運輸小車的減振性能，從而降低果品在運輸過程中的損傷，并對履帶小車的減振結構的研究提供了一定的參考。