電驅動系統可靠性目標載荷快速構建方法研究

鄧思城 ，趙禮輝 ，2，3，王 震 ，周 馳 ，鄭松林 ，2，3

（1.上海理工大學 機械工程學院，上海 200093；2.機械工業汽車機械零部件強度與可靠性評價重點實驗室，上海 200093；3.上海新能源汽車可靠性評價公共技術平臺，上海 201108）

可靠性是新能源汽車的重要技術指標，也是當前影響其用戶認可度的主要因素。電驅動系統作為新能源汽車的主要動力源（純電動、增程式、燃料電池的唯一動力源），其可靠性是整車可靠性的重要構成部分，直接關系到整車的運行安全[1]。在汽車研發體系中，基于車輛服役載荷的可靠性設計、分析和試驗是保障其在用戶使用條件下可靠性水平的重要方式，其中能夠復現不同用戶車輛行駛過程中性能退化的工況載荷則是開展這些工作的前提。

由于駕駛行為、載重狀態、路面起伏、交通狀況各不相同，電驅動系統在不同用戶使用條件下載荷差異巨大，為保證用戶使用過程中車輛的可靠性，試驗載荷需要覆蓋足夠的用戶百分位水平（如95%），即目標載荷。可靠性目標載荷的構建，需要以大量用戶樣本數據為基礎。直接通過用戶車輛進行載荷采集的方式成本高、周期長，用戶樣本量往往較低[2]；仿真方法成本低、載荷獲取快速，是車輛載荷獲取的重要方式。然而，行駛路況與外部環境的隨機性[3]，使仿真結果與實際用戶載荷偏離較大，進而影響整體損傷水平的確定。

多年來，國內外研究人員圍繞車輛運行數據（含載荷數據）和運行狀態間的相互關系開展了大量研究，取得了豐碩的成果。張抗抗[3]等研究了電動車行駛阻力的貢獻量，確定車輛運行過程中行駛阻力隨著坡度的增加基本呈正比增加。夏光等[4]指出道路坡度與整車質量為影響車輛行駛阻力的主要參數，而風阻與滾動阻力系數基本固定，在速度較低時的影響可以忽略不計。FATHY等[5]以實測車輛運行數據為基礎，結合整車質量上下限收斂，采用遞歸最小二乘法，得到行駛過程中車輛質量的有效估計。RAJAMANI等[6]和KIM等[7]基于實采懸架加速度和位移數據，采用平均法對整車動力學模型中的質量參數進行了估算。VAHIDI等[8-10]提出了一種平均估算法，基于車速、縱向加速度等信息實現了車輛質量、行駛阻力和道路坡度估計。雷雨龍等[11]通過縱向動力學模型，基于擴展卡爾曼濾波方法實現了車輛質量及道路坡度估計。諸文博等[12]通過提取驅動力信號和縱向加速度信號的高頻部分，使用遞歸最小二乘法進行車輛質量與道路坡度估算。郝勝強等[13]通過穩態卡爾曼濾波法估算整車質量與道路坡度。綜上研究可知，目前研究多聚焦于通過車速、驅動力、縱向加速度等運行數據估計車輛行駛道路坡度與整車質量等運行狀態，較少開展反向研究。文獻[3]和文獻[4]雖然給出了與驅動力相關的影響因素，但并未進一步形成有效估計方法。在電驅動系統可靠性載荷構建過程中，不同用戶使用條件下的車速信息相對容易獲取，但轉矩、轉速等載荷信息往往缺失。鑒于坡道、質量等因素對驅動系統載荷的強相關性，如何考慮這些因素的影響，并通過已有車速數據構建有效的電驅動系統可靠性目標載荷，尚缺乏有效方法。

為此，本文提出一種基于不同用戶車輛歷史車速數據的電驅動系統可靠性目標載荷構建方法。以整車動力學仿真模型為基礎，通過等效質量和等效坡度的參數優化，實現用戶長期使用過程中仿真載荷與實際載荷損傷及頻次分布的一致。進一步結合全體用戶損傷累積分布，通過百分位損傷水平下參數統一，構建覆蓋一定用戶使用強度的電驅系統可靠性目標載荷，從而為快速準確地進行電驅動系統可靠性評估與壽命預測奠定基礎。

1 整車及電驅動系統動力學建模

1.1 整車參數

本文研究的車輛為某品牌的新能源汽車，其基本參數見表1。

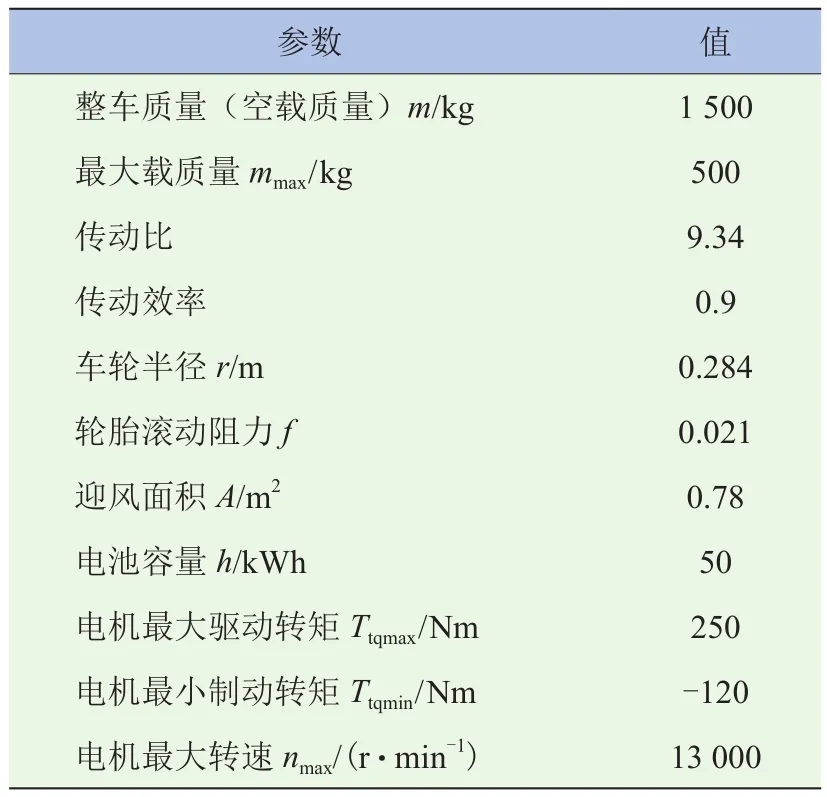
表1 整車基本參數

1.2 整車及電驅動系統數學模型

根據整車在行駛過程中的阻力與驅動力關系，可知整車受力平衡方程[14-15]：

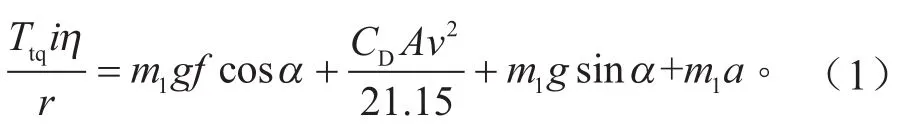
式中：Ttq為電機軸轉矩，Nm；i、η分別為總傳動比和傳動效率，組成減速器模型；r為輪胎半徑，m；m1為整車等效質量，kg；f為輪胎滾動阻力系數，取值為[16]為空氣阻力系數；A為迎風面積，m2；α為等效坡度，%，組成車身模型；v為車速，m/s；a為汽車加速度，m/s2。

根據減速器模型，得到的電機轉速，結合轉矩可由式（2）[17]計算電機功率：

式中：n為電機轉速，r/min。

本研究著重考量電驅動系統載荷，不涉及功率損失，將汽車行駛過程中電機驅動功率近似等于電池輸出功率，忽略輔助功率器件的影響，可得：

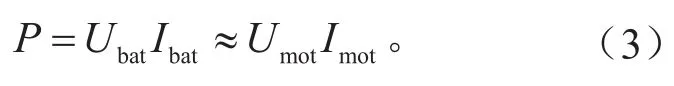
式中：Ubat、Ibat分別為電池輸出電壓和電流；Umot、Imot分別為電機輸入電壓和電流。

由此可以求得電池電壓、電流變化與剩余SOC，從而構成電池模型。制動模塊根據前后車輪抱死情況進行分析[18-19]，得到制動控制模塊。整車模型以式（1）為基礎，連接數學模型，建立整車動力學仿真模型，如圖1所示。

圖1 電動汽車整車動力學仿真模型

1.3 仿真參數影響

1.3.1 等效參數分析

以40位用戶車輛歷史服役時長為2年的數據為基礎，又以車速數據和電機軸轉矩數據為對象進行研究，使用第1年數據進行分析，第2年數據對比驗證。鑒于整體數據量較大，從中選取10位用戶進行不同參數設置下仿真載荷單位里程損傷強度對比分析，10位用戶的行駛時間和里程如圖2所示。

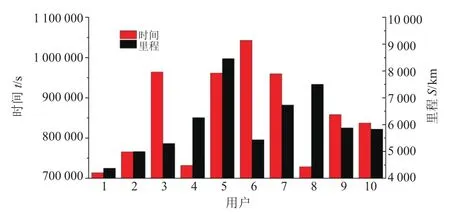
圖2 行駛時間和里程

車輛行駛過程中的道路坡度α、車輛載質量mv對整車動力學仿真結果具有重要影響，而同一等效參數的仿真結果對不同用戶優劣各異。為對比等效參數的變化對仿真轉矩造成的損傷變化和時域分布的影響，以及各用戶仿真損傷精度的差異性，以3種狀態進行載荷仿真（表2），并與實際載荷進行比較分析。

表2 整車載荷仿真狀態參數

基于仿真載荷數據，結合S-N曲線和Miner線性損傷累積理論[20-21]，各用戶單位里程損傷結果如圖3所示。參數為狀態1時，10位用戶都未達到預期損傷水平，在狀態2和狀態3時，部分用戶損傷有較高精度，前者對損傷的提升最高可達50%，后者最高可達30%。各狀態參數下用戶仿真損傷與實際損傷進行分布擬合，服從對數正太分布，累積概率分布如圖4所示，不同狀態參數下95%損傷覆蓋水平皆未達到實際效果，狀態1參數下相差最大。

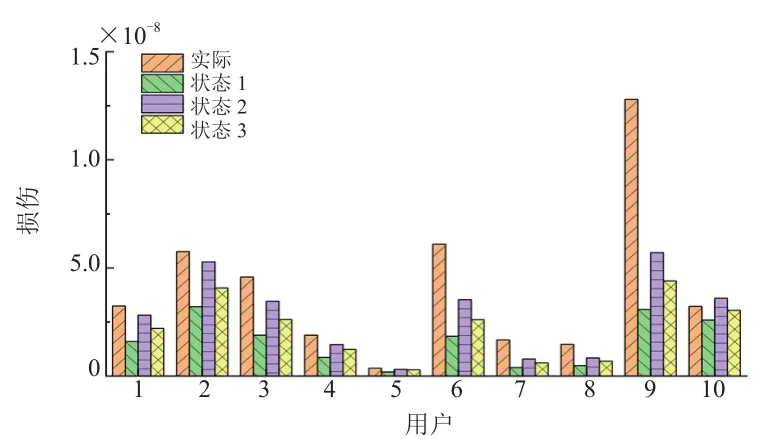
圖3 用戶不同參數仿真損傷

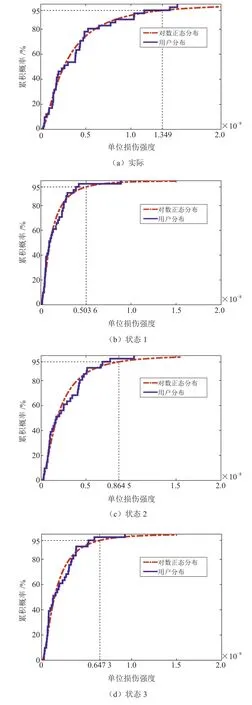
圖4 損傷累計概率分布

以圖2中5號用戶為例進行時域分布對比。對變程分布和幅值分布進行歸一化處理，結果如圖5和圖6所示。狀態1參數下的仿真載荷在兩種分布下與實際偏離最大，參數為狀態2時偏離最小，仿真最大變程為實際的0.92倍，正向幅值大小都符合實際水平。

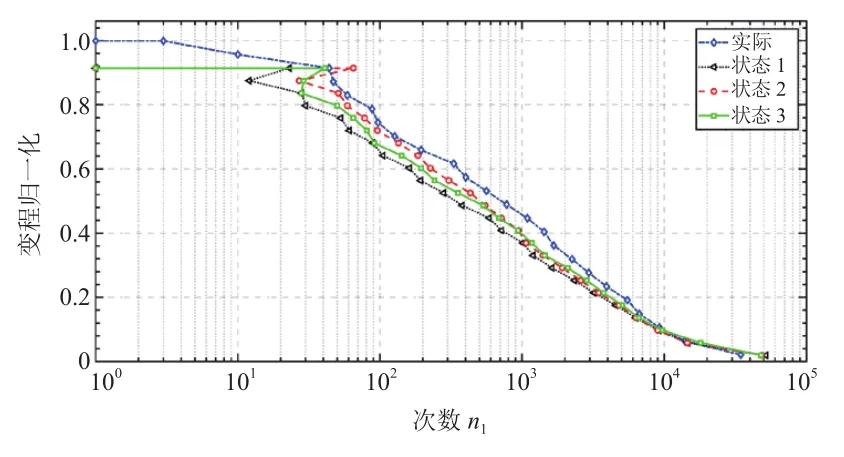
圖5 變程分布

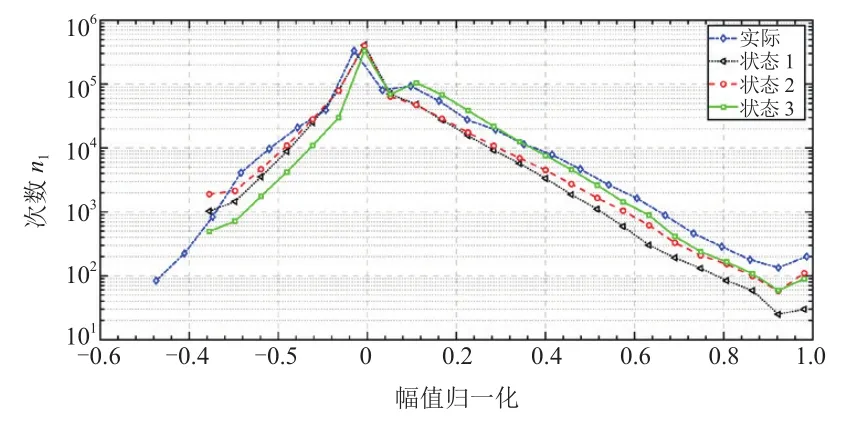
圖6 幅值分布

通過對比分析可知，行駛坡度與載質量對轉矩損傷強度和時域分布都有較大的影響，且不同用戶難以基于同一參數仿真得到高精度載荷數據。

1.3.2 用戶不同時段損傷一致性分析

對于每個用戶，其駕駛行為相對固定，行駛路線及載質量狀態具有高頻分布特征，所以同一用戶不同時間段駕駛工況的劇烈程度存在一定的關聯性。通過模型仿真，研究200組隨機參數狀態下用戶群體第1年與第2年數據仿真載荷95%損傷水平下相對實際的誤差，如圖7所示。兩者誤差差值絕對值對比如圖8所示，最大值為14%左右，大部分處于10%以下；其大小隨著兩者誤差的減小而減小，當誤差小于10%時較小，為1%左右。兩者誤差的Pearson相關性為0.996，相關性極強。因此，對于該用戶群體，仿真載荷損傷百分位水平越接近實際，后續構建的目標載荷可靠性覆蓋度更準確。

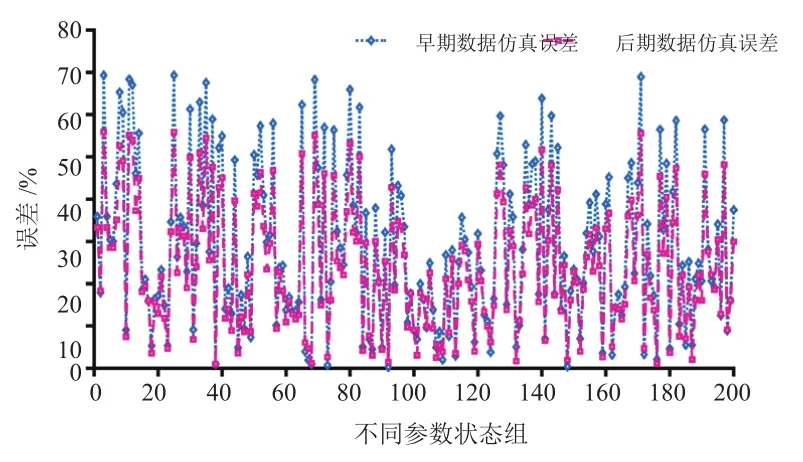
圖7 95%損傷水平誤差對比

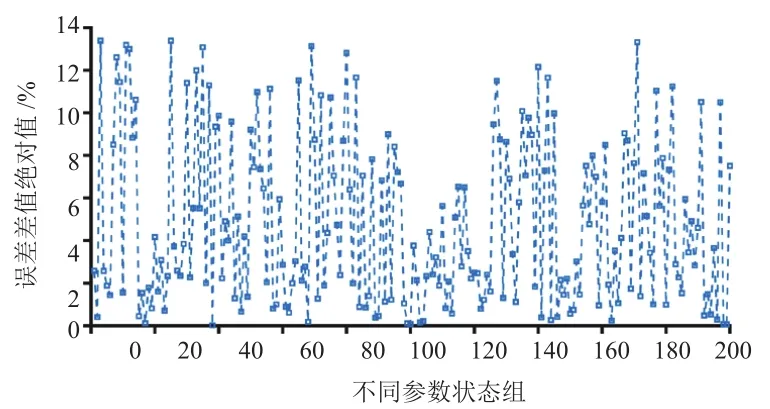
圖8 誤差差值絕對值對比

2 損傷與等效參數的函數擬合

為建立以損傷強度為目標的優化數學模型，構建電機軸損傷強度隨行駛坡度d和整車質量m變化的函數關系式。

由表1可知，車輛最大載質量為500 kg；上坡路段對車輛轉矩的影響要遠大于下坡[22]，且大部分道路坡度要小于12%。將1 500 ～2 000 kg整車質量等間隔100 kg、坡度0～12%等間隔1%進行仿真，以圖2中1號用戶為例，各等級參數下仿真轉矩單位損傷強度見表3，損傷分布如圖9所示。隨著二者參數的單獨增加，損傷均呈線性增加。

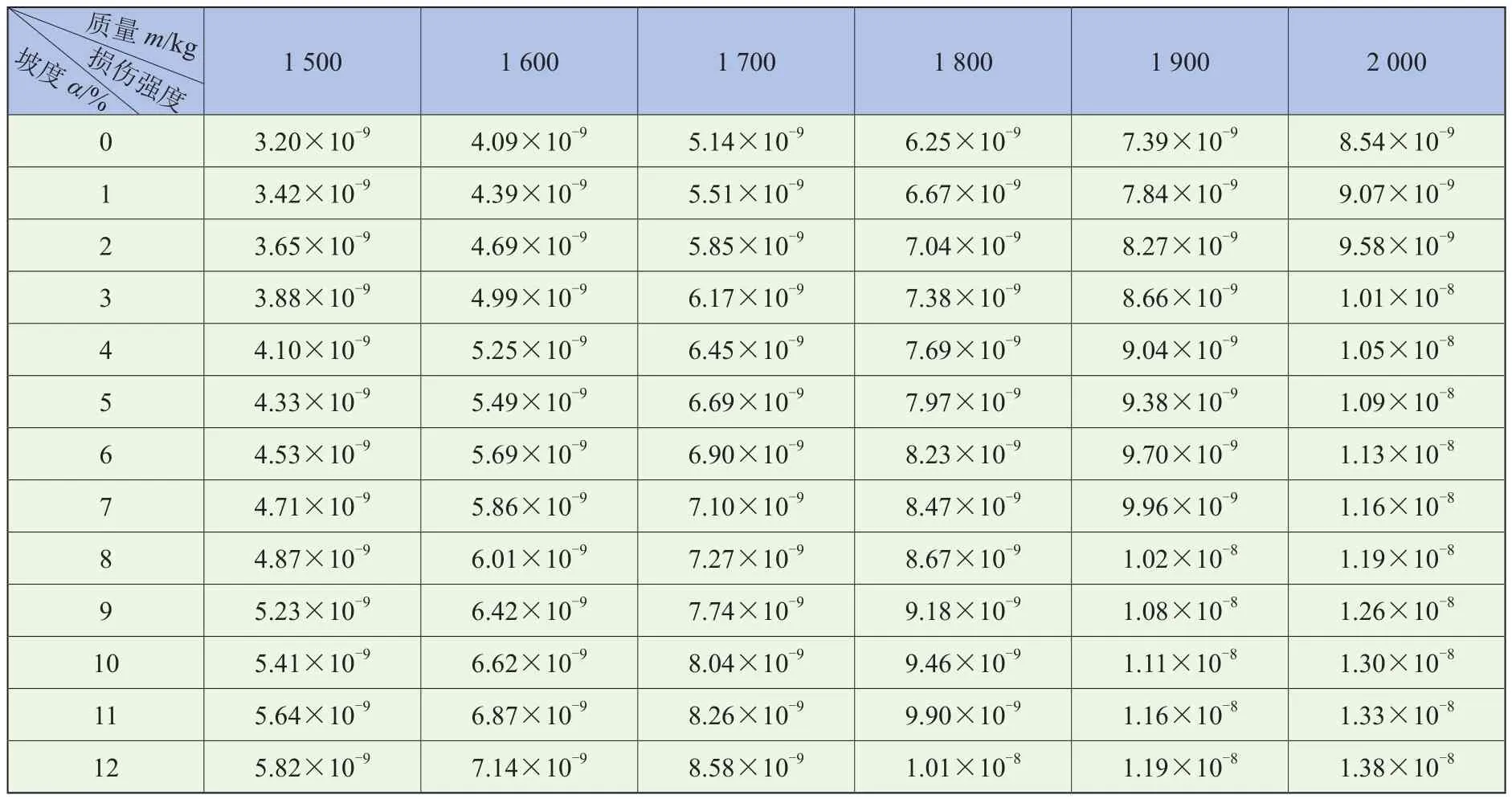
表3 各等級參數下單位損傷

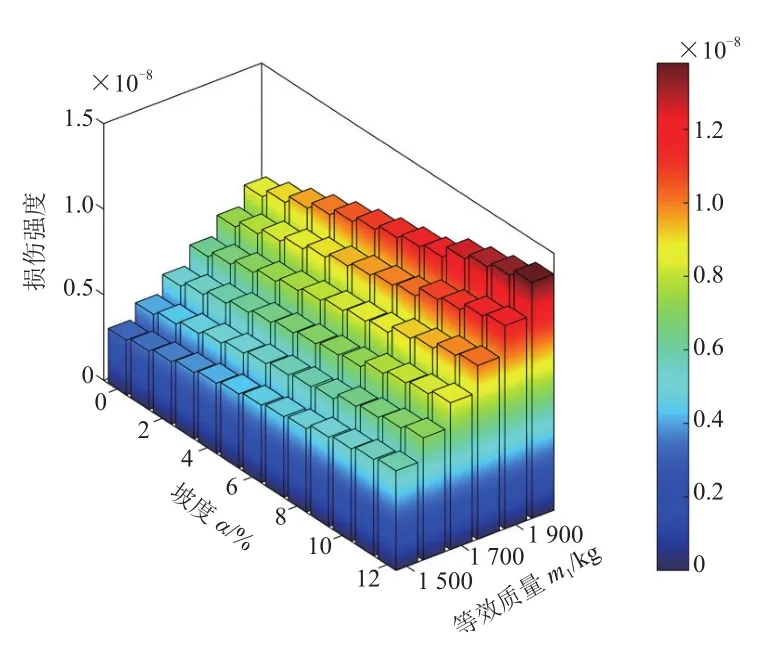
圖9 各等級參數損傷分布

根據表2數據，擬合出1號用戶單位損傷強度關于整車等效質量、行駛坡度的近似函數關系式為：

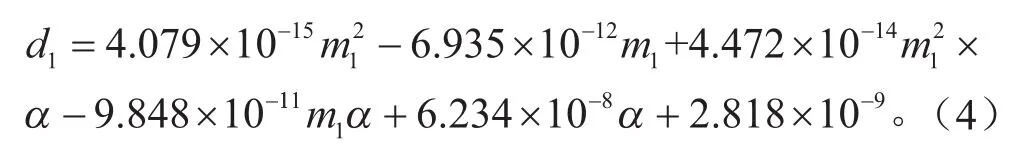
考慮車輛實際狀態，整車等效質量及坡度取值區間如下：1 500 kg≤m1≤2 000 kg，0≤α≤12 %。使用擬合的函數關系式，對各等效質量和坡度進行損傷計算，擬合誤差如圖10所示，最大為3%左右。

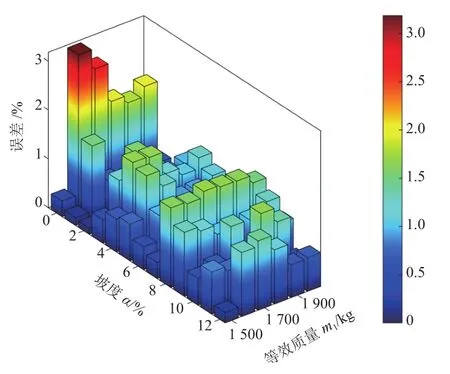
圖10 各等級損傷誤差

3 單個用戶參數優化

3.1 參數優化模型

3.1.1 損傷強度優化目標函數構建

將實際損傷與擬合損傷的函數關系做差的絕對值，定義為轉矩損傷的優化目標函數：

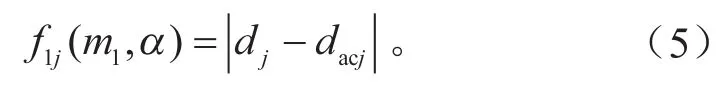
式中：f1j、dj、dacj分別為第j位用戶的損傷目標函數、損傷數學模型和實際損傷值。

3.1.2 時域分布優化目標函數構建

考慮仿真轉矩時域分布效果，根據式（1）對任意時刻仿真與實際轉矩做差的絕對值作為目標函數時，會引入大量方程，得到復雜解。將各時刻轉矩差值求和，能有效減少計算量、得到統一解。由于制動時受到制動策略控制，不完全符合式（1）。將仿真與實際驅動正轉矩各時刻的差值絕對值求和，根據式（1）得：

式中：nj為第j位用戶驅動轉矩出現的總次數；Ti、Taci為第i次出現的仿真和實際驅動轉矩。

由表3可知坡度取值小，則可令：

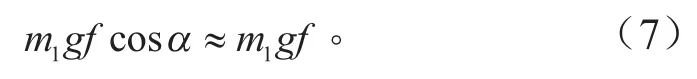
根據三角不等式可得：

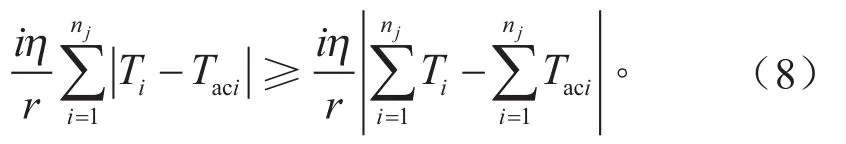
根據式（7）和式（8），第j位用戶的轉矩時域分布優化目標函數定義為：

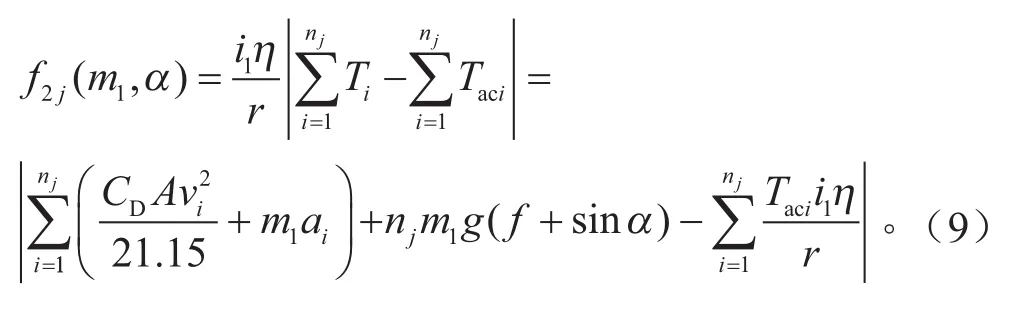
將采集的歷史服役數據計算求和，可得式（9）各項系數。

3.1.3 變量及約束條件

以道路坡度和整車等效質量作為變量，以兩者正常取值區間作為約束條件，具體為：

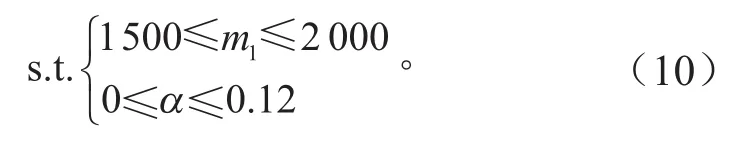
3.1.4 優化模型

根據式（5）～（10），可將第i位用戶的仿真轉矩多目標優化問題進行如下描述：

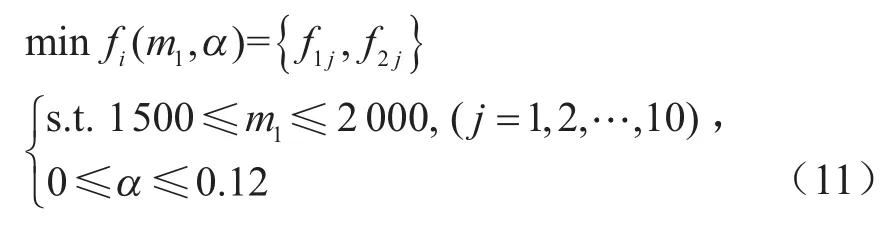
3.2 優化結果分析

結合優化模型為典型的多變量、多目標優化模型，采用非支配排序遺傳算法-II（Non-Dominated Sorted Genetic Algorithm-II，NSGA-II）對不同用戶進行參數優化求解[23]。各用戶參數經200次迭代，可得到等效坡度和等效質量Pareto最優解。選取的10位隨機用戶對應的最優解見表4，其中用戶5的坡度解最大，用戶7的整車質量解最大，而9號用戶坡度和質量解都處于較高水平，單位損傷強度高。基于優化參數進行仿真，與實際損傷最大誤差為4.08%。群體用戶仿真與實際損傷服從對數正太分布模型，累計概率分布如圖11所示，兩者95%期望損傷水平基本一致。

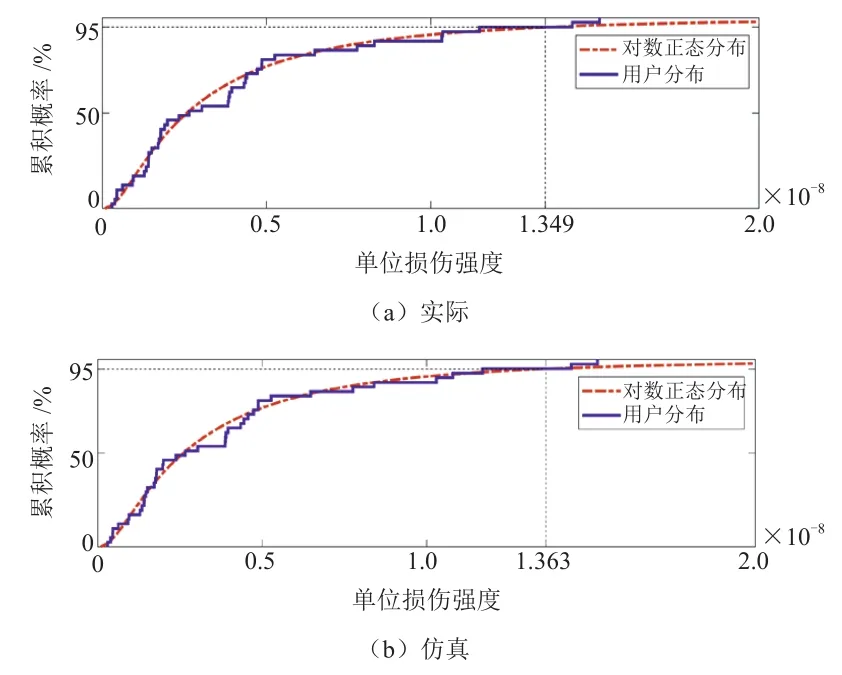
圖11 損傷累積概率

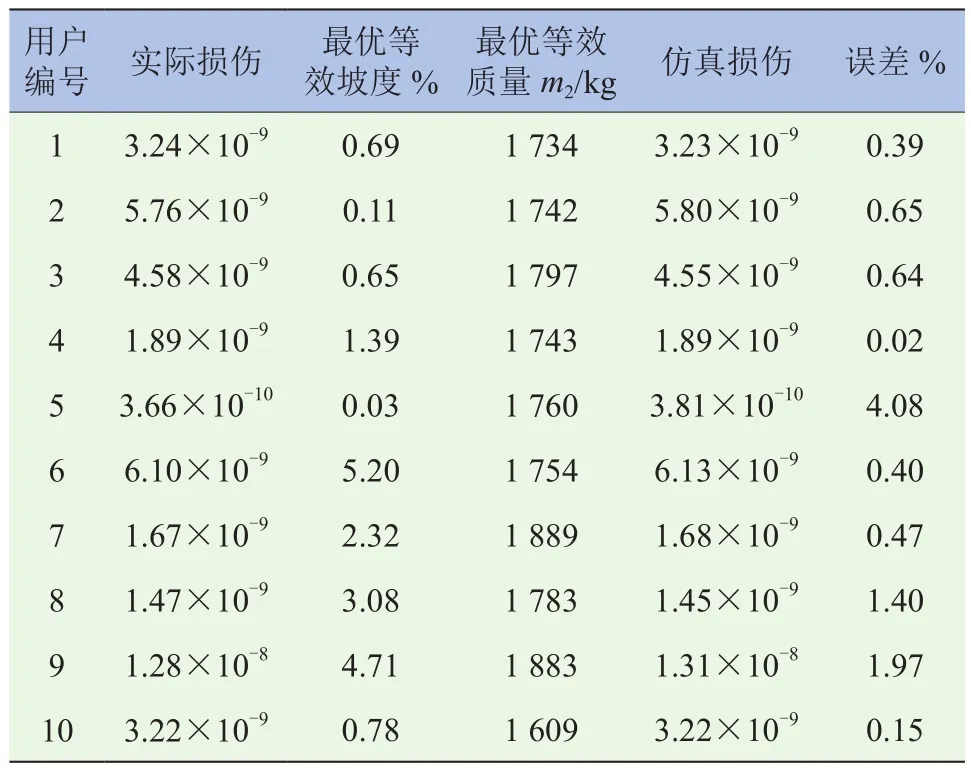
表4 實際與仿真轉矩單位損傷對比表

以損傷相對誤差最大的用戶（5號）為例進行說明，兩個時間段內的轉矩相對變化如圖12所示，轉矩歸一化處理后，優化參數仿真載荷極值與實際載荷極值吻合度更高。變程與幅值分布如圖13和圖14所示，參數優化后仿真載荷幅值分布更為貼近實際，在幅值較大時明顯，且正向振幅頻次顯著提高，近似實際分布。

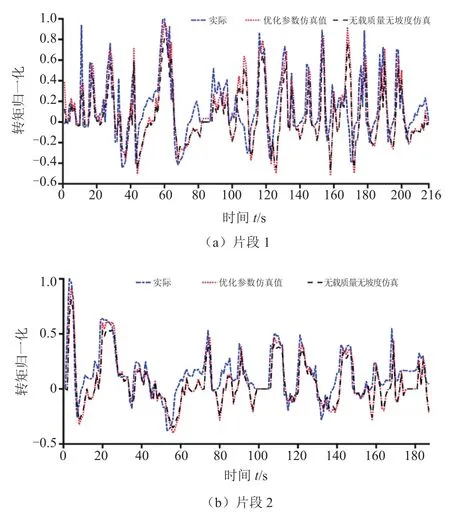
圖12 轉矩時間歷程片段

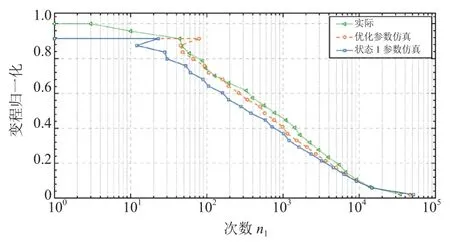
圖13 變程分布

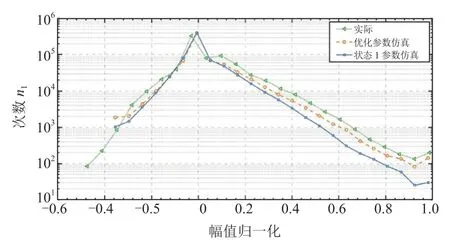
圖14 幅值分布

4 群體用戶參數統一

4.1 參數統一的優化模型構建

對Y～N(0,1)，可知：

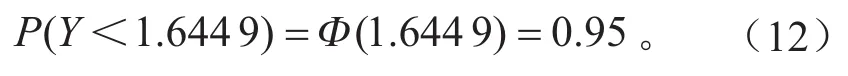
由圖4和圖11可知，仿真與實際用戶損傷服從對數正態分布。根據式（12），以群體用戶仿真和實際轉矩損傷取對數的平均值、標準差和對應95百分位損傷作差的絕對值定義為目標函數：

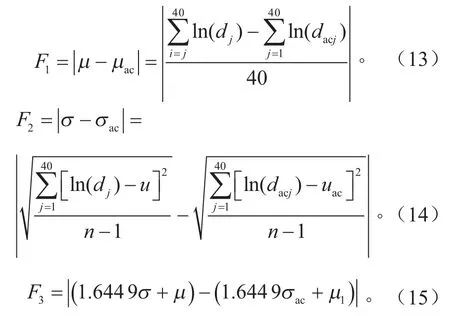
根據式（9），將各用戶轉矩時域分布優化目標函數求和獲得以群體時域分布作為目標函數：

變量和約束與式（10）相同，構建優化數學模型：

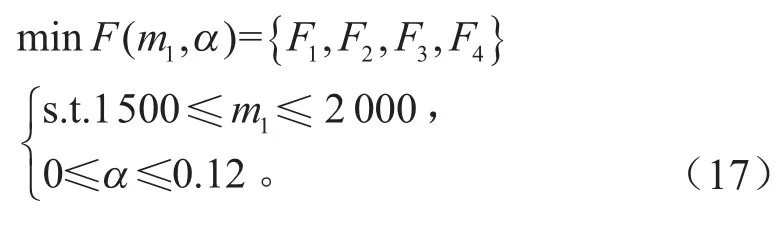
4.2 結果分析

基于第1年運行數據，對群體用戶模型參數優化求解，得到對采用所有用戶參數的統一最優解：等效坡度和質量分別為5.23%和1 779 kg。95%損傷期望水平與實際基本對應，如圖15所示。基于此參數對用戶第2年服役數據進行仿真驗證，同樣滿足實際載荷的95%損傷期望水平，如圖16所示。

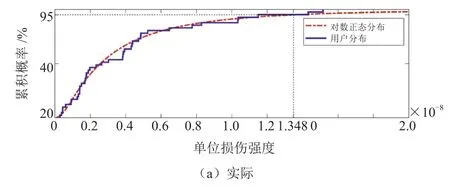
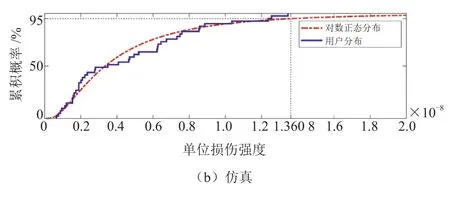
圖15 用戶第1年損傷累積概率分布

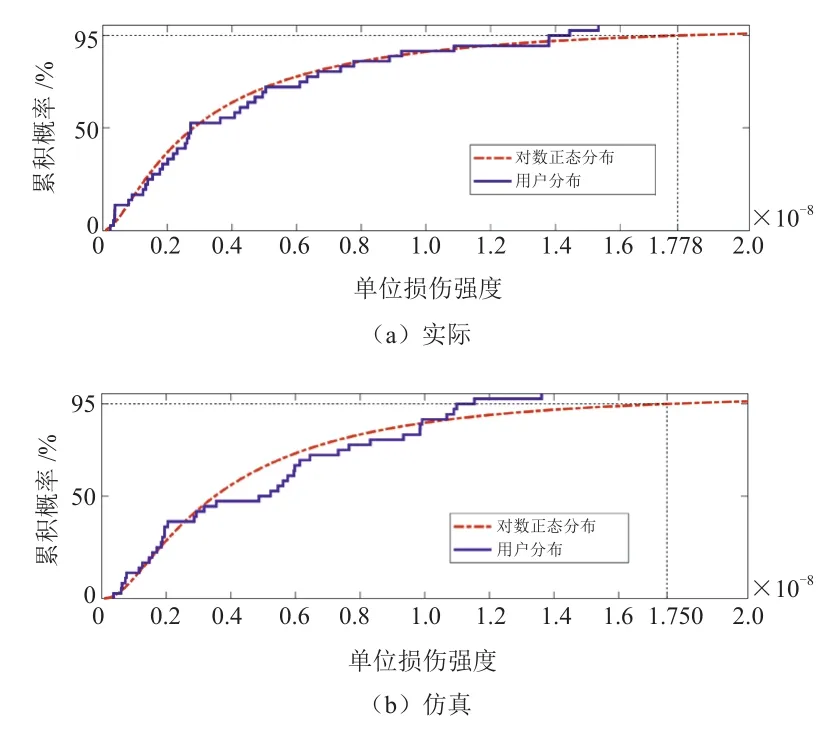
圖16 用戶第2年損傷累積概率分布

圖17為1號用戶最優參數與統一參數的仿真轉矩對比實際轉矩變程的歸一化分布，參數統一后的仿真轉矩在變程小于0.8倍最大變程時分布與實際吻合度更高，在大于0.8倍時則相反。

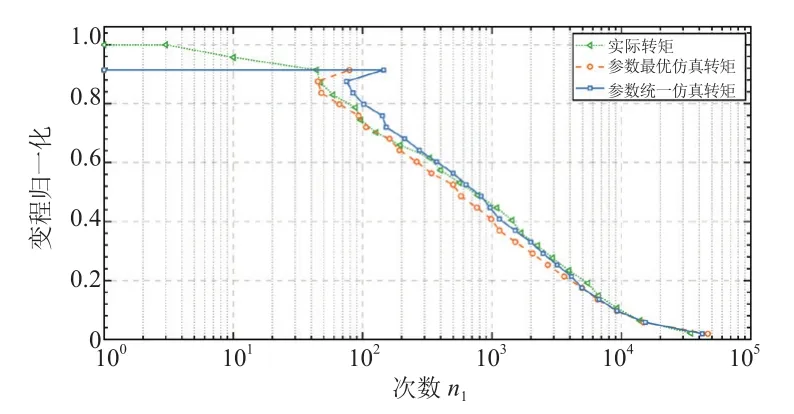
圖17 變程分布

結論證實了基于用戶運行車速數據仿真構建可靠性目標載荷的研究方法的有效性。

5 結論

本文基于用戶運行數據對道路坡度和整車質量模型參數進行優化，提出了電驅動系統可靠性目標載荷快速構建方法，并通過仿真與實際運行數據對比驗證該方法的有效性。主要結論如下：

（1）根據整車數學模型建立仿真模型。由于工況的差異性，分析了在不同載質量與坡度狀態參數下，用戶仿真載荷的損傷精度、時域分布效果均不相同；在隨機參數狀態下，通過研究用戶群體在不同時期仿真載荷的95%損傷水平與實際的誤差，驗證了用戶不同時期工況劇烈程度有極強相關性。

（2）計算各等級參數下仿真轉矩損傷，擬合得到損傷關于坡度和質量的函數關系式，驗證了該函數的損傷計算精度。以此為基礎，結合整車動力學平衡方程，構建不同用戶的優化數學模型，對比實際轉矩和空載無坡度參數下的仿真轉矩，基于優化參數的仿真轉矩損傷誤差小，時域分布良好，95%損傷期望水平與實際基本一致。

（3）構建以參數統一、獲取可靠性目標載荷為目的的數學優化模型，基于統一參數對整體用戶進行轉矩仿真，95%損傷水平基本對應實際，第2年服役數據同樣滿足條件；對比了用戶時域分布，有較高精度。

本研究方法為電驅動系統可靠性目標載荷快速構建提供了一定參考，起到減少載荷樣本采集量、加速電驅動系統可靠性評估與壽命預測的作用。