基于核學習的運動目標跟蹤算法綜述

婁佳欣 李元凱 王媛 徐琰珂

摘 要：核方法通過將原始空間數據映射到高維希爾伯特空間， 將非線性映射隱含在線性學習器中， 使用核函數代替高維空間中復雜的內積運算， 能夠有效避免高維空間計算帶來的“維數災難”。 核方法具備可學習性、? 高效計算、? 可線性化、? 泛化性能好等優勢， 為解決非線性目標跟蹤問題提供了一種新的有效途徑。 傳統的目標跟蹤方法往往利用跟蹤模型預測目標當前運動狀態， 并確保跟蹤的準確性與實時性， 核方法則提供了線性化處理的一般途徑， 且可以不依賴具體模型， 具備高效計算能力， 將核學習方法引入目標跟蹤領域有望提升目標跟蹤的環境適應性。 本文基于核方法基本思想， 著重梳理了核學習目標跟蹤當前的研究進展， 包括基于核學習的目標檢測算法、? 生成式和判別式目標跟蹤算法， 以及構造不同核函數的多核學習方法， 并對核學習目標跟蹤在核函數優化、? 長時間跟蹤、? 特征提取、? 目標遮擋等方面的進一步研究與探索進行展望。

關鍵詞： 核學習方法; 非線性映射; 目標檢測; 目標跟蹤; 多核學習; 模式識別

中圖分類號： ?TJ760; TP18? 文獻標識碼：??? A? 文章編號： 1673-5048（2021）05-0064-12

0 引? 言

核方法即基于核的學習（Kernel-Based Learning）， 是在統計理論基礎上發展起來的一種新的學習方法， 是模式識別領域的一個新興分支， 最初應用于支持向量機。 核方法通過非線性映射將原始空間數據映射到高維特征空間， 可以在樣本空間內進行線性分析， 是處理非線性模式識別問題的有效方法。 同時， 核方法還可以提供高效計算的途徑， 利用核函數將非線性映射隱含在線性學習器中進行同步計算， 使用核函數代替高維空間中復雜的內積運算， 為解決高維空間計算復雜度及“維數災難”問題提供了一種新思路。 核方法結構簡單， 泛化性能好， 不存在過學習問題， 算法理論上得到的是全局最優點， 可避免局部極值問題。 核方法還可以將經典的線性算法， 如卡爾曼濾波、? 主成分分析等， 無損推廣為非線性形式， 應用于運動目標跟蹤、? 圖像識別等非線性問題， 為非線性問題的線性處理提供一種理想手段。 目前， 核方法已經在支持向量機、? 核主成分分析、? 時間序列預測、? Fisher鑒別分析等方面有應用先例。

在新興技術驅動下， 目標跟蹤技術加速發展， 涉及模式識別、? 動態系統、? 人工智能等眾多學科， 在智能決策[1]、? 無人駕駛[2-4]、? 生物醫學[5]、? 人機交互、? 軍事偵察等領域， 已經取得重要應用并有巨大的發展前景。 運動目標跟蹤問題， 本質上是一類典型的非線性模式識別問題， 通過運動目標的先驗知識建立跟蹤模型， 預測目標當前時刻或當前幀的運動狀態和運動規律。 然而， 跟蹤模型的質量直接影響跟蹤效果， 跟蹤模型較差， 如目標運動狀態不匹配或搜索區域設置不合理， 將會導致明顯的跟蹤誤差甚至目標丟失。 基于核方法的運動目標跟蹤算法利用非線性映射關系的構建和學習， 可以不依賴于具體模型， 在目標運動狀態非線性變化情況下依然能夠保證跟蹤質量， 讓目標跟蹤具有更好的環境適應能力。

由于核方法具備高效計算、? 泛化性能好、? 數據驅動等優點， 學者們嘗試將核方法進一步引入目標跟蹤領域， 以建立非線性、? 高精度、? 強魯棒的適應性目標跟蹤模型。 目前， 基于核方法的目標跟蹤算法也不斷涌現， 跟蹤模型更精準、? 數據驅動更合理、? 運算速度更快捷， 目標跟蹤能力得到有效提升。

本文梳理了基于核方法的運動目標跟蹤算法的研究現狀， 論述了基于核方法的目標檢測算法以及生成式和判別式目標跟蹤算法的研究進展， 并針對核函數的設計與研究， 討論了具有多核函數的典型多核學習方法以及構造方法與應用范圍， 最后探討了核學習目標跟蹤的研究與應用前景， 展望了其在長時間跟蹤、? 目標尺度變化、? 核函數優化、? 特征提取準確性等方面的發展趨勢。

1 核映射思想

核方法是通過固定非線性映射算子將原始空間數據映射到再生希爾伯特空間（Reproducing Kernel Hilbert Space，? RKHS）， 在高維特征空間進行數據分析和處理的方法。 再生希爾伯特空間是一種由核函數構成的帶有內積的完備向量空間， 由于映射過程難以顯性表達， 在該空間中， 往往采取計算核函數代替映射內積的方式進行算法推導， 以避免對特征映射的直接求解。

航空兵器 2021年第28卷第5期

婁佳欣， 等： 基于核學習的運動目標跟蹤算法綜述

定義非線性映射算子為核函數 κ ， 對所有的 x ， ?x′ ， 核函數滿足

κ（x， x′）=〈φ（x）， φ（x′）〉 （1）

式中： φ（·） 是由原始空間變換到特征空間的特征向量。

當核函數滿足連續、? 正定、? 對稱時， 稱為Mercer核[6]。 如果核函數滿足以下兩個條件：

（1） 對任意的 x∈X， ?κ（x， z） 中向量的函數歸屬于向量空間F;

（2） ?κ（x， z） 滿足可再生性，

則為可再生核函數， 而一個確定的可再生核函數即定義了一個可再生希爾伯特空間。 其中， 核函數滿足的可再生性是指核 κ（x， ·） 組成的函數：

g（·）=∑li=1aiκ（ci， ·） （2）

對于所有的 i ， ?ci∈X， 滿足

〈g， κ（x， ·）〉=∑liaiκ（ci， x）=h（x） （3）

通過Mercer核定義， 得到再生核的表示形式為

κ（x， x′）=∑∞i=1ζiφi（x）φi（x′） （4）

式中： ζi 和φi分別為非負的特征值和特征向量， 映射φ可表示為

φ： X→F

φ（x）=[ζ1φ（x1）， ζ2φ（x2）， …] ?（5）

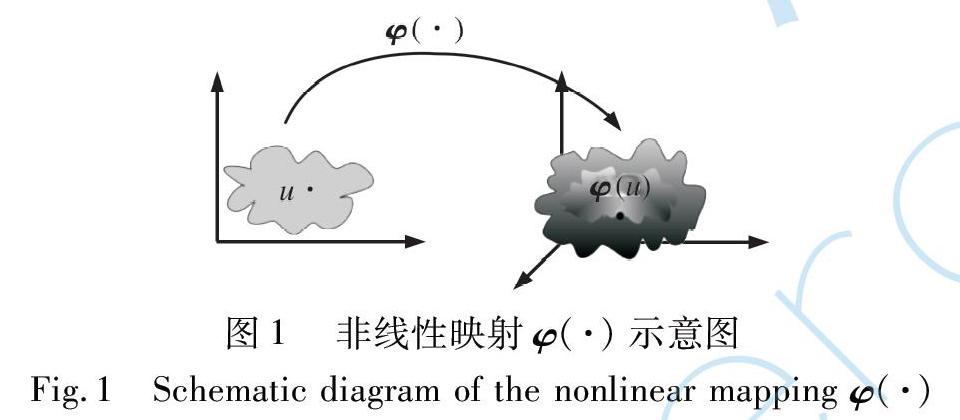
對于原始輸入空間的數據 u ， 通過φ（·）映射到特征空間中， 得到φ（u） ， 如圖1所示， 圖中給出了數據從原始空間到希爾伯特空間的映射關系。

在希爾伯特空間中， φ（·）為由原始空間到特征空間的映射， φ（x） 為映射后的特征向量， 對所有的 x， x′∈X，? 核函數都滿足

φ（x） T φ（x′）=κ（x， x′） （6）

即在映射函數φ（·）難以顯性表達的情況下， 通過計算核函數代替再生希爾伯特空間中復雜的映射內積計算， 從而簡化計算過程， 提供高效計算能力。

2 核學習運動目標跟蹤

目標跟蹤技術是智能系統領域的一個富有挑戰性的分支， 旨在實現對目標運動模態的識別和決策， 具有廣闊的應用前景和重要的研究價值， 已經應用在智能監控、? 無人駕駛、? 生物醫學、? 人機交互、? 軍事瞄準等領域。 核方法由于其可線性化、? 數據驅動等優點， 被廣泛應用在目標跟蹤算法中， 并取得了豐碩的成果。

目標跟蹤主要包括外觀模型、? 運動模型、? 搜索策略三部分， 涉及圖像處理、? 數據處理、? 機器學習等方面。 考慮到目標檢測是目標跟蹤的前提， 基于核方法的運動目標跟蹤流程可描述為： 基于目標狀態信息檢測， 根據目標跟蹤模型預測目標運動趨勢， 進行更高層次的目標行為分析和決策。 根據建立的目標外觀模型的不同， 可以將目標跟蹤分為生成式跟蹤方法和判別式跟蹤方法。

2.1 目標檢測

目標檢測是目標跟蹤的前提， 直接影響跟蹤效能。 基于核方法的目標檢測算法主要有核主成分分析（Kernel Principal Component Analysis，? KPCA）、? 核Fisher判別分析（Kernel Fisher Linear Discriminant，? KFLD）、? 核獨立成分分析（Kernel Independent Component Analysis，? KICA）算法。

2.1.1 KPCA算法

核方法使用核函數代替高維空間的內積運算以解決高維計算復雜問題， 在支持向量機上得到了成功應用。 受到核方法的啟發， 早在1998年， Scholkopf等[7]將核方法與主成分分析結合起來， 提出了核主成分分析（KPCA）， 該算法使得核方法脫離支持向量機與其他算法結合起來， 并有效用于形態特征提取與目標檢測領域， 對于核技巧的廣泛應用具有重要意義。

主成分分析法（PCA）是最小均方意義上的最優變換， 需求取樣本協方差的特征值和特征向量， 通過特征值和特征向量的提取突出原始數據的隱含信息， 以去除隨機向量之間的相關性， 從而得到數據的主要成分。

KPCA算法則首先對目標訓練圖像集進行訓練， 計算各樣本的KPCA特征， 然后截取待檢測圖像中的子圖像， 計算子圖像的KPCA特征， 再通過計算檢測函數來檢測目標是否存在。 KPCA算法是PCA的非線性推廣， 通過核函數將原始空間數據映射到希爾伯特空間， 在希爾伯特空間中利用重構誤差最小準則， 使用PCA算法重構原圖像。 與PCA算法相比， KPCA提取了目標高階統計特征， 可以讓目標描述更加充分完整。

2.1.2 KFLD算法

Fisher線性判別（Fisher Linear Discrimination，? FLD）或線性判別式分析（Linear Discriminant Analysis，? LDA）由Mika在1999年提出。 FLD是基于樣本類別進行整體特征提取的有效方法， 其在PCA算法降維的基礎上考慮到訓練樣本的類間信息， 基本原理是找到一個最合適的投影軸， 使各類樣本在該軸上投影之間的距離盡可能遠， 而每一類內的樣本投影盡可能緊湊， 使分類效果達到最佳， 即在最大化類間距離的同時最小化類內距離。 FLD算法在進行圖像整體特征提取方面有著廣泛的應用。

Mika等[8]隨后將FLD算法擴展到非線性領域， 提出了KFLD算法， KFLD檢測算法繼承了KPCA算法的思想， 也可以提取目標的高階統計特征， 不同的是， KFLD是在特征空間執行Fisher線性判別， 得到特征空間中基于描述的最優分類， 從而得到更精準的目標特征提取。

2.1.3 KICA算法

KPCA和KFLD目標檢測算法為核方法的發展奠定了基礎， 2002年， Bach等[9]提出了核獨立成分分析（KICA）， 進一步豐富了核檢測算法。

獨立成分分析（ICA）是從多元/多維統計數據中尋找潛在因子或成分的一種算法。 該算法基于對比函數定義， 可尋找滿足統計獨立和非高斯的成分， 其中的對比函數是根據對單個固定非線性函數的期望， 以一種特殊的方式選擇一個固定的非線性函數， 使函數期望對互信息產生一個穩健的逼近。

KICA則提供了一種新的路徑來解決獨立分量分析問題， 基于非線性的整個函數空間處理核希爾伯特空間中的函數， 并利用核技巧在空間上高效搜索。 函數空間的使用使其能夠適應各類數據樣本， 從而使算法對變化的樣本分布更具魯棒性。

2.2 生成式跟蹤

生成式跟蹤方法是指在線學習建立跟蹤目標的特征模型， 以此目標特征模型為模板， 通過特征模型對圖像進行搜索和匹配， 找到與原始圖像重建誤差最小的區域， 并以此區域作為跟蹤目標的定位， 同時， 利用統計分布模型判斷后續圖像中是否有相應的特征描述模型和目標概率模型， 最終實現對目標實時有效的跟蹤。

生成式模型跟蹤方法的主要代表之一是均值漂移跟蹤算法（Mean Shift，? MS）。 均值漂移是一個在迭代中尋找最優解的過程， 以任意樣本為中心劃定區域， 在該區域內尋找概率密度最大的點， 然后以該點為中心重復上述過程， 直到符合收斂條件。

2.2.1 均值漂移算法原理

MS算法在跟蹤初始時刻需要自主確定搜索窗口來選擇目標， 是一種半自動跟蹤算法。 該算法計算初始幀搜索窗口的直方圖分布， 并以同樣的方法計算第 N 幀窗口的直方圖分布， 讓搜索窗口沿直方圖密度增加最大的方向移動， 最終得到目標的位置。? 流程如下：

（1） 初始幀的目標模型

將特征空間按像素顏色值分為多個特征值， 初始幀的搜索窗口中第 u 個特征值的概率為

q～u=C∑ni=1κx0-xih2δ[b（xi）-u] （7）

式中： ?x0 ， ?xi 分別為第 n 幀搜索窗口的中心像素坐標和第 i 個像素的坐標; ?h 為核函數的帶寬; ?κ（·） 為核函數。

（2） 第 N 幀模型

計算第 N 幀搜索窗口中第 u 個特征值的概率為

p～u（y）=Ch∑nki=1κy0-xih2δ[b（xi）-u] （8）

式中： ?y0 為搜索窗口中心像素的坐標。

（3） 相似性函數

相似性函數是表征初始幀與第 N 幀目標模型的相似程度， 相似性函數定義為

ρ～（y）≡ρ（ρ～（y）， q～）=∑mu=1ρ～u（y）q～u （9）

（4） MS向量

對相似性函數求最大值， 可以得到MS向量：

mh， G（y）=y1-y0=∑nki=1xiwigy～0-xih2∑nki=1wigy～0-xih2-y0 （10）

式中： ?y0 和 y1 分別為搜索窗口和新窗口的中心坐標。

2.2.2 研究進展

MS算法最早在1975年由Fukunaga等[10]提出， 起初并沒有受到人們的廣泛關注， 直到1995年， Cheng[11]在原MS的基礎上加入核函數和權值系數， 極大地擴展了MS理論。 隨后Comaniciu等[12-15]首先將MS算法引入視頻圖像處理中， 實現了MS算法的圖像平滑、? 分割、? 跟蹤。 文獻[16]證明， 對于既定核函數， MS算法可以收斂到數據中心， 為MS算法在目標跟蹤領域應用打下基礎。 文獻[17]中提出了MS目標跟蹤算法， 引入核函數的MS算法跟蹤速度快、? 魯棒性強， 使得MS算法成為目標跟蹤領域的主流算法之一， 得到學者廣泛的關注和大量的研究改進。

MS跟蹤算法中核函數帶寬固定， 導致目標尺寸發生變化時跟蹤誤差較大。 為此， 在尺度空間理論[18]的基礎上， Collins提出了一種可變尺度的MS跟蹤算法[19]。 文獻[20-21]提出了參數的自適應選擇方案， 在目標尺度變化時依然可以取得較好的跟蹤精度， 從而對MS跟蹤算法作了進一步擴展。

MS算法中的顏色特征圖無法準確描述目標顏色在圖像中的分布， 容易導致特征空間空缺。 針對此類問題， 文獻[22]在目標跟蹤模型中引入空間顏色直方圖， 將目標顏色與當前幀中的圖像顏色結合在一起， 提高了目標的識別精度。? 文獻[23]提出了基于聚類顏色模板的MS算法， 文獻[24]則在跟蹤中加入目標的外接矩陣尺寸， 對當前幀進行分塊處理， 提出了基于自適應分塊顏色直方圖的MS目標跟蹤算法。 文獻[25]在顏色特征直方圖中融入空間信息， 在 X ，? ?Y 方向上分解目標， 得到6個顏色的特征直方圖。 文獻[26]多角度全方位提取目標特征得到目標顏色直方圖， 提高了目標識別精度。 為了提高目標跟蹤的魯棒性， 文獻[27]在描述目標特征時采用cross-bin顏色直方圖， 提高了MS算法的魯棒穩定性。

為了減少背景對目標跟蹤的影響， 文獻[28-31]基于背景加權直方圖的MS算法提出核修正方案， 可以有效抑制和分離背景， 改善跟蹤效果， 實現復雜背景下精度更高的目標跟蹤。

為了提高MS算法的抗遮擋能力， 學者們還嘗試將多種濾波算法融入MS算法中[32]， 并取得了較好的跟蹤效果。 文獻[33-38]提出在MS算法中使用卡爾曼濾波（Kalman Filter，? KF）算法預測目標位置， 在目標被短暫遮擋時提高跟蹤精度。 文獻[39-40]則使用KF對核函數直方圖進行濾波， 及時更新目標跟蹤模板， 提高了目標的抗遮擋能力和跟蹤精度。 文獻[41-43]在均值漂移迭代的過程中， 利用粒子濾波框架重新分配隨機粒子， 更新樣本均值， 彌補了目標特征描述不足的缺陷， 然而對于小目標與背景邊緣處的區分能力仍有欠缺。

為了改善目標跟蹤過程中由于旋轉、? 尺度變化導致跟蹤精度下降的情況， 文獻[44]有效解決目標發生旋轉時的跟蹤不穩定問題， 之后文獻[45]又提出了基于核函數的仿射目標跟蹤算法， 但是兩種算法的跟蹤速度較慢， 無法滿足實時跟蹤的要求。 文獻[46]改進了對稱核函數， 在MS目標跟蹤算法中引入非對稱核函數， 對于復雜形狀的目標區域取得了較好的跟蹤效果， 但是對于有較大彈性的非剛體目標， 目標跟蹤效果不理想。 文獻[47]提出了一種新的相似度函數， 利用特征空間模型[48-49]可以跟蹤一般幾何變化的目標。 文獻[50]在MS算法中引入變換核函數， 并且融入了目標邊緣信息， 可以實時調整目標模型跟蹤仿射變化的運動目標。

為了對多目標物體和人體關節進行跟蹤， 文獻[51]在MS算法中引入置信融合傳播算法， 可以實現對單目標、? 多目標、? 人體關節的跟蹤。 文獻[52]使用多個跟蹤器互相協作， 通過子空間約束這些跟蹤器， 從而能夠跟蹤非剛體目標和人體的各個關節。

為了提高目標跟蹤的準確性和魯棒性， Topkaya等[53]在似然映射融合框架內， 結合獨立分類器的輸出進行MS跟蹤， 并引入了一種新的似然融合算法， 把不同二值分類器得到的似然映射作為跟蹤置信值。 Wang等[54]提出了一種改進的基于目標位置預測的MS跟蹤算法， 該算法利用幀間的聚類運動估計和尺度估計來預測MS算法在每次迭代中的初始搜索位置。 Yu等[55]提出了一種基于優化目標外觀模型和在線更新策略的強魯棒性MS算法。 Zeng等[56]提出了一種新的局部特征描述模式， 稱為四叉二值模式（QBP）， 與局部二值模式（LBP）相比， QBP對復雜場景下的特征提取具有更強的魯棒性， 計算復雜度更低。 Phadke等[57]通過加入對變化不敏感的特征來增強魯棒性， 提出平均局部二值模式（Mean Local Binary Pattern， MLBP）、? 光照不變特征、? 改進的模糊C均值（Modified Fuzzy C Means， MFCM）、? 加權顏色直方圖等來處理光照和尺度變化， 以進一步提高目標跟蹤的準確性。 Liu等[58]提出了兩個重要的機制來進一步提高跟蹤器的魯棒性， 一是使跟蹤器能夠意識到潛在的干擾， 并對外觀模型做出相應的調整; 二是使跟蹤器能夠檢測并從完全遮擋引起的跟蹤失敗中恢復。

經過20多年的發展， MS算法在目標跟蹤領域取得了豐碩的成果， 在實時性和魯棒性等方面也有較好的表現。 MS算法具有計算量小、? 易于實現、? 調節參數少、? 實時性高等特點， 在聚類、? 圖像平滑、? 圖像分割、? 視頻監控等領域都有成功的應用。 近年來， 關于MS算法的研究已經相對成熟， 但是MS算法也存在很多待解決的問題， 如只適用于短時間的目標跟蹤， 在長時間目標跟蹤的情況下， 魯棒性和跟蹤精度逐漸降低; 目標模型只采用了顏色特征描述， 容易受背景的干擾; 目標尺度發生較大變化或被遮擋時， 跟蹤精度下降。

MS算法作為核密度估計算法的典型代表， 是生成式跟蹤的主要算法。 生成式跟蹤算法固然可以取得較好的跟蹤效果， 但是忽略了背景及周圍環境的信息， 跟蹤過程很容易受到背景干擾。 因此， 如何將目標與背景有效分離顯得尤為重要。

判別式跟蹤算法充分利用背景和環境信息分別對目標特征和背景特征建模， 可以有效將目標與背景分開處理， 于是判別式跟蹤算法的研究在目標跟蹤領域逐漸得到重視和應用。

2.3 判別式跟蹤

判別式跟蹤方法引入機器學習的相關理論， 對目標特征和背景特征分別建模， 以置信圖中的峰值作為目標位置， 通過訓練相應的濾波器將目標和背景區分開。 相比于生成式跟蹤算法， 判別式跟蹤可以更好地得到目標在當前圖像中的具體位置， 且識別精度高、? 跟蹤速率快， 因此被廣泛研究。 基于核方法的判別式目標跟蹤可分為核函數循環檢測跟蹤算法和核相關算法兩部分， 其中， 核相關算法跟蹤速度快、? 精準度較高， 得到更多重視。

2.3.1 核函數循環檢測跟蹤算法

相關濾波在頻域有較快的運算速率， 對目標的跟蹤速度可以達到每秒數百幀， 是實現目標實時跟蹤的有效途徑。 2010年， Bolme等[59]將相關濾波引入到MOSSE （Minimum Output Sum of Square Error） 算法中， 開創了目標跟蹤從時域擴展到頻域的先河。 MOSSE算法利用了相關濾波在頻域計算速度快的特點， 跟蹤速度可以達到669幀/秒， 同時還具備優良的目標定位性能， 后續許多研究均是以此為基礎展開的。

2012年， 在MOSSE算法的基礎上， Henriques等[60]提出了基于核函數循環檢測跟蹤（Circulant Structure of tracking-by-detection with Kernels， CSK）算法。 CSK算法的特點是利用循環矩陣的相關理論， 對訓練樣本和候選樣本進行循環移位， 以增加兩個樣本的數量， 同時使用訓練樣本訓練分類器， 利用訓練好的分類器在候選樣本構造的候選區域內進行檢測， 相關計算中響應的最大值則為目標的位置。 為進一步提高計算速度， CSK算法中引入了核函數， 將數據從原始空間中引入高維希爾伯特空間， 算法使用快速傅里葉變換， 使得整個運算過程在傅里葉域內進行。

為了找到響應位置， CSK算法須從頻域變換到時域， 這會導致邊際效應， 類似于非周期信號在系統中的泄露現象。 同時， CSK算法應用范圍較窄， 只適用于灰度特征空間， 對目標外觀模型的建立有所欠缺， 容易受復雜任務背景和環境噪聲干擾。 為了更精確地建立目標外觀模型， Danelljan等[61]在CSK算法的基礎上使用顏色空間（Color Name，? CN）以加強對表觀模型的描述， 將三維顏色空間映射入高維CN空間中， 算法可以更加有效地建立目標外觀模型， 對目標部分遮擋、? 光線變化、? 復雜背景等情況也有較好的跟蹤效果。 但由于高維空間計算的復雜性， 引入三維顏色空間后， CSK算法的計算速率降低。

核函數循環檢測跟蹤算法在目標尺度發生變化或被遮擋時， 跟蹤精度明顯下降， 為此， 后續又提出了其他基于相關濾波的目標跟蹤算法， 取得了比CSK算法更好的跟蹤效果和跟蹤魯棒性。

2.3.2 核相關算法

為進一步提高跟蹤精度和跟蹤效果， Henriques等[62]提出核相關濾波跟蹤算法（Kernelized Correlation Filters，? KCF）。 該算法加入窗函數， 保證圖像的周期性， 減弱了邊際效應; 同時引入核技巧， 將原始樣本空間映射到高維空間中， 利用離散傅里葉變換對角化的性質減少存儲和計算量， 提高了模型計算效率; 此外， 引入方向梯度直方圖特征取代CSK中的灰度特征， 提取目標紋理和方向特征， 可以實現對目標快速有效的跟蹤。

KCF算法構建了一整套核化濾波理論體系， 先通過循環移位構造大量的訓練樣本， 再利用核技巧、? 傅里葉變換等操作避免矩陣逆運算， 極大減少了計算量， 實現對目標的快速準確跟蹤， 因此在目標跟蹤領域逐漸發展壯大， 涌現出了更多的后續研究。

KCF算法典型過程主要包括嶺回歸[63]、? 循環矩陣對角化、? 核相關濾波、? 目標快速檢測4個過程：

（1） 嶺回歸

對于線性回歸初始模型， 優化目標函數為

f（x）=W T Xs（11）

在樣本Xs中找到權值 Wi 使對目標 Yi 的預測最小化：

min ω∑i（f（xi）-yi）2+λw2 （12）

式中： ?λ 為擬合控制參數。 對式（12）求導置零， 最優解為

w=（XsHXs+ λI）-1XsH y （13）

式中： Xs為樣本矩陣; ?y 為標簽。

（2） 循環矩陣

記Xn×1={x1， x2， …， xn} T為正樣本， 訓練樣本即負樣本通過正樣本循環移位得到。 使用負樣本訓練分類器， 一維循環移位算子 P 為

P=000…1100…0010…000…10 （14）

向量x通過不斷與循環移位算子 P 相乘， 得到 n 個向量組合的一維圖像的循環矩陣C（x）。 對于二維圖像， 通過在感興趣區域內循環移位， 可以得到二維圖像訓練樣本， 最終得到二維矩陣的循環矩陣。

（3） 核相關濾波器

為了改善分類器性能， 將原始空間數據映射到高維空間， 權重 ω 為輸入樣本的線性組合

ω=∑iαiφ（xi） （15）

引入核化技巧φT（x）φ（x′）=κ（x， x′） ， 式中最優解可以轉換為

α=（K+λI）-1y （16）

式中： K為循環矩陣。

利用循環矩陣的性質整理式（16）為

α^=y^k^xx+λ （17）

式中： ?kxx 為循環矩陣K的第一行; ?y^ 為 y 的離散傅里葉變換。 一般情況下， 可通過對 α^ 的計算來求解分類器。

（4） 目標快速檢測

設上一幀目標狀態為 x ， 當前幀輸入樣本為 z ， 引入核矩陣K得到測試樣本的響應， 即

f^（z）=k^xz⊙α^ （18）

對式（18）進行傅里葉逆變換得到樣本的響應值， 以響應值中最大值的位置作為目標的位置， 然后更新分類器參數和目標模型：

xi=（1-θ）xi-1+θziαi=（1-θ）αi-1+θσi ?（19）

式中： ?xi 和 αi 分別為第 i 幀預測的目標位置模型和分類器參數; ?zi 和 σi 為檢測到的目標位置模型和分類器參數; ?θ 為學習率。

2.3.3 研究進展

傳統目標跟蹤算法， 如均值漂移算法、? 卡爾曼濾波算法[64]、? 基于貝葉斯濾波的粒子算法[65]、? 根據目標特征的TLD（Tracking Learning Detection）跟蹤算法[66]、? 基于壓縮感知（Compressive Tracking， CT）的跟蹤算法[67]， 在跟蹤精確度和運算速度方面性能欠佳。 核相關算法則結合了CSK算法運算速度快的優勢， 對分類器訓練和樣本檢測等方面都做了改進， 在目標跟蹤精度和識別成功率等方面都有了很大提升， 再利用方向梯度直方圖特征使算法在跟蹤速度方面也具備很好的性能， 超過了同期其他主流算法。

然而， KCF算法局限于對目標位置的跟蹤， 并沒有考慮目標尺寸變化或目標被遮擋等情況， 使得在實際跟蹤中得到的目標分布區域與實際位置有所偏差。 同時， KCF算法在更新目標模型時會產生大量的正負樣本， 在進行長時間跟蹤或目標尺寸發生變化時容易丟失跟蹤。 針對這些問題， 大量文獻對KCF算法展開進一步研究。

為了解決目標跟蹤過程中尺度變化、? 目標被遮擋、? 目標丟失等問題， Danelljan等[68]在KCF中引入尺度金字塔， 在位置估計基礎上， 增加一個濾波器進行目標尺度估計， 通過位置濾波器估計目標在當前幀中的位置， 再使用尺度濾波器檢測目標尺度變化， 以應對跟蹤過程中目標尺度發生變化的情況。 該算法比原KCF算法在跟蹤精度上有所改善， 但模型計算復雜度明顯增加， 使得目標跟蹤的實時性無法得到保證。 在此基礎上， Li等[69]提出基于自適應尺度的核化相關濾波算法（SAMF）， 不再進行儲存性訓練， 只使用一個濾波器， 但在進行每次尺度測量時， 需要多進行一次特征值提取和傅里葉變換。 該算法雖然簡化了計算， 但在圖像較大時， 仍無法滿足實時跟蹤的要求。 王守義[70]提出了基于卷積特征的KCF算法， 該算法在高層和低層分別提取目標特征， 再利用卷積神經網絡計算高層和底層的響應圖， 將兩層響應圖進行融合， 實現目標在當前幀的位置估計。 該算法改善了目標尺度變化時跟蹤效果變差的問題， 但是當目標被遮擋， 仍不能達到較好的跟蹤效果， 魯棒性較低[71-73]。 文獻[74]提出多尺度相關濾波目標跟蹤算法， 使用可塑性強和穩定性強的兩種嶺回歸模型， 可塑性強的模型跟蹤目標位置并以位置為中心構建圖像金字塔， 穩定性強的模型預測目標尺度變化， 算法可以實現多尺度檢測與跟蹤。 文獻[75]提出了深度縮放核相關濾波器（Depth Scaling Kernelized Correlation Filters， DSKCF）， 將KCF中的RGB目標跟蹤算法通過融合深度特征擴展為RGB-D跟蹤算法， 改善了目標尺度變化及目標被遮擋等問題。 為了應對在跟蹤過程中丟失目標等問題。 劉延飛等[76]利用響應圖中峰值數據的均值和標準差修正每幀中的峰值， 改善了KCF算法中長時間目標跟蹤的問題。

為應對KCF算法中循環移位產生的邊際效應問題， Danelljan等[77]引入空間整定因子約束濾波權重， 以犧牲算法的運算速度有效緩解了邊際效應。 阮宏剛[78]提出基于稀疏特征的快速尺度的核自適應濾波算法， 在原KCF算法的基礎上引入帶寬可調的高斯窗， 結合相關濾波和稀疏特征估計目標位置， 并預測尺度變化， 可以更好地將目標與背景分離。

現有KCF算法在更新模型時使用固定學習率， 容易發生跟蹤漂移現象。 為此， Asha等[79]提出了學習率的動態調整， 通過前后幀中目標的位置變化來更新變化率。 陳智等[80]在響應圖中設置峰值、? 閾值， 峰值大于閾值時更新跟蹤模型。 Wang等[81]分析利用響應圖來判斷目標是否發生漂移， 但是當目標尺寸變化時， 會導致模型更新不準確的狀況。

對于復雜場景， 單一核難以滿足跟蹤性能需求， KCF算法的多核融合是一種自然延展的方案。 文獻[82]提出了用于視覺跟蹤的邊緣多核相關算法（LMKCF）， LMKCF主要利用低秩張量學習來減輕多核相關濾波器在學習和更新中的冗余和噪聲， 建立了前瞻性的學習和更新策略。 文獻[83]提出了一種約束多核相關跟蹤算法（CMKCF）， 建立了具有三種不同屬性的多通道特征的多核模型， 在半核矩陣上使用一個空間裁剪算子來解決邊界效應。 文獻[84]在KCF算法中引入TSK-FLS （Takagi Sugeno Kang-Fuzzy Logic System）， 提出了模糊核相關濾波器（Fuzzy Kernel Correlation Filter，? FKCF）算法。 FKCF算法中采用TSK模糊系統前件映射代替核映射， 通過后件參數改進算法， 在目標劇烈運動時， FKCF算法跟蹤精度有所提升。 文獻[85]將多項式核與高斯核模糊化處理， 得到魯棒性更強的核函數， 從多核融合的角度提出了多模糊核相關濾波器（Multiple Fuzzy Kernelized Correction Filter，? MFKCF）， 算法有更高的跟蹤精度與適應性。 為了降低跟蹤過程中的累計誤差， 文獻[86]提出了基于時空顯著性的雙核自適應濾波算法（KCFSS）， 通過時空顯著性方法搜索姿態穩定的局部區域， 該區域對累計誤差有較低的敏感度， 有助于減少累計誤差， 然后在原目標與顯著區域之間建立雙核跟蹤模型， 可對目標跟蹤位置進行微調。 受核協同方法在人臉識別等領域成功應用的啟發， 文獻[87]提出基于核協同的目標跟蹤算法（Kernel Collaborative Presentation with L2 Regularization，? KCRL2）， 將字典矩陣映射到高維空間， 同時引入L2正則最小均方， 加快計算速度， 以獲取更高的跟蹤精度。

針對紅外目標跟蹤中圖形信息量少， 目標特征不足等問題， 學者們也對KCF算法進行了深入研究， 確保KCF算法在紅外目標跟蹤領域的跟蹤效果。 Battistone等[88]采用局部分析和結構化向量機的方法， 在紅外目標VOT比賽中取得了很好的名次。 為解決KCF中尺寸固定的問題， Montero等[89]提出了SKCF算法， 在KCF算法中引入可調高斯窗函數和尺度估計模型， 在紅外目標跟蹤中的跟蹤精度較高。 鄭武興等[90]則在KCF算法中融入灰度和顯著性特征， 所提算法可以有效用于空中紅外目標的跟蹤。

3 多核學習

核函數設計是核學習目標跟蹤算法中的重要環節， 是影響跟蹤性能的關鍵因素。 在不同應用場景下， 單個核函數會表現出很大差異， 對于復雜場景， 單個核函數難以滿足目標形狀復雜、? 數據不規則、? 環境復雜、? 樣本不平坦分布或規模巨大等實際應用需求。 研究表明， 多個核函數的融合可以提高復雜場景下的跟蹤效果。 近年來， 大量學者開始研究多核學習方法[91-98]。 該方法中的多核模型是一種靈活性、? 魯棒性更強的核學習模型， 相關實驗[99]也證明了多核模型能夠獲得比單核模型更好的跟蹤性能。 現有多核學習方法主要有合成核、? 多尺度核、? 無限核3種典型方法。

3.1 合成核方法

合成核方法是多核學習的基本方法， 合成核的構造主要有5種方法： 多核線性組合合成方法、? 多核擴展合成方法、? 非平穩多核學習、? 局部多核學習、? 非稀疏多核學習[100-101]。 在樣本數據量較復雜的情況下， 合成核方法得到的核函數跟蹤精度較高。

合成核方法是較為通用的多核學習方法， 在圖像的目標識別領域有廣泛的應用。 文獻[102]在金字塔框架下描述目標形狀時采用多核表示。 文獻[103]采用合成核方法獲得了基于決策的目標類別的稀疏依賴圖， 實現了多類目標檢測， 提高了目標識別精度。 同時， 合成核方法還可以利用多核組合的稀疏性和分類器， 將學習問題轉換成不同的優化問題[104-105]， 通過多特征空間的整合進行快速求解[106]。 另外， 合成核方法也在目標特征值的提取和處理[107-108]、? 分類[109-112]、? 圖像分割處理[113]、? 系統辨識[114]等方面也得到了成功應用。

3.2 多尺度核方法

合成核方法是利用簡單核函數的線性組合得到新的核函數， 而簡單的線性組合方式在處理樣本不均衡分布情況時不能取得較好的跟蹤精度， 從而限制了決策函數的表示能力。 多尺度核方法引入尺度空間， 將多個尺度的核函數融合成一個靈活的新的核函數。 多尺度核方法不是簡單的核函數線性組合， 其需要為每個核函數訓練各自的帶寬， 帶寬較小的核函數用于跟蹤變化劇烈的樣本， 帶寬較大的核函數用于跟蹤變化比較平緩的樣本。 多尺度核方法與合成核方法相比， 可以提高跟蹤精度， 但是運算量較大， 在目標跟蹤實時性方面表現不佳， 因此普適性比較低， 后續研究并不豐富。

對多尺度核方法進行適當擴展利于提高跟蹤性能， 文獻[115]將多尺度核進行了分類， 提出典型的多尺度核方法。 文獻[116-117]將多尺度核方法用于時間序列預測和非平坦函數的估計， 提出了多尺度支持向量機回歸。 文獻[118]結合多尺度核方法在希爾伯特空間中對再生核進行函數重構。 文獻[119-121]將多尺度核方法應用到高斯建模中， 推進了多尺度核方法的發展。

3.3 無限核方法

合成核方法和多尺度核方法是將有限個核函數線性組合或融合在一起， 然而對于大規模數據處理， 有限核組合成的多核處理方法不一定達到預期跟蹤效果， 決策函數也不一定能表現到最優。 因此， 由有限個核函數向無限核擴展是多核學習的一個發展趨勢。 目前， 核函數主要局限在高斯核函數（Gaussian Kernel）、? 多項式核函數（Polynomial Kernel）、? 線性核函數（Linear Kernel）、? 指數核函數（Exponential Kernel）、? 拉普拉斯核函數（Laplacian Kernel）這幾種， 設計空間比較小， 并且有限核在較復雜的情況下往往也可以取得滿意的跟蹤效果， 因此無限核方法在目標跟蹤方面的應用較少。

多核學習建立了更靈活、? 適應范圍更廣、? 魯棒性更強的核學習模型， 在動態系統時間序列預測、? 信號和圖像的濾波、? 壓縮和超解析、? 故障預報、? 文本分類、? 圖像處理、? 目標檢測、? 視頻跟蹤、? 生物信息學（雙螺旋、? 基因序列數據分類、? 蛋白質功能預測）等領域已有應用。

4 發展趨勢展望

基于核方法的目標跟蹤算法目前已有一定成果， 與其他跟蹤方法相比在非線性處理、? 數據驅動、? 不依賴模型等方面具有一定優勢。 然而在實際應用場景中， 現有算法還難以很好地滿足實時性、? 準確性、? 魯棒性、? 適應性等多種需求。 因此， 基于核方法的目標跟蹤算法存在較大的研究和探索空間， 主要體現在以下幾個方面：

（1） 降低跟蹤模型的依賴性

傳統的貝葉斯目標跟蹤算法， 如卡爾曼濾波、? 粒子濾波等算法， 對系統模型和模型參數的先驗信息有較高要求， 但在非線性處理或算法運行速度等方面表現不足。 將核方法引入經典目標跟蹤算法中， 可以擴展算法在非線性處理方面的應用， 同時核函數代替樣本空間的內積運算， 避免復雜的高維運算。 目標動力學模型可以通過訓練測量數據構造的條件嵌入算子來描述[122]， 以降低跟蹤算法對具體動態系統模型的依賴。

（2） 提高特征提取的準確性

視覺跟蹤是目標跟蹤領域的熱點， 特征提取的優劣是影響視覺目標跟蹤效能的關鍵因素。 提高特征提取的準確性可通過多特征融合和深度卷積特征實現。 在提取目標特征時， 與人工特征相比， 卷積特征有一定的優勢[123-125]， 但選取何種網絡訓練特征仍需要進一步的研究和探索。 單一特征描述目標具有局限性， 多特征融合可以更加精確地描述目標外觀特征[126-127]， 將目標與背景更好地區分開， 然而多特征融合及特征之間參數的調節會增加計算復雜度， 如何在提升跟蹤性能的同時確保跟蹤速度， 是需要權衡的問題。

（3） 提高基核設計的均衡性

對于復雜場景， 單個核函數難以滿足復雜場景下的跟蹤任務， 多核學習方法可以應對復雜任務場景下單一核跟蹤不精確的問題， 通過多個基核的組合優化核函數， 調節與優化多個基核的權系數和其他參數， 以應對復雜應用場景。 但多核學習方法在適應更復雜應用場景的同時也會增加算法計算量， 因此研究高效的學習算法是必要的。 另外， 多核學習框架的均衡設計也有進一步深入探索的空間。

（4） 提高環境變化的適應性

現有的目標跟蹤算法在一般情況下可以實現穩定的跟蹤， 然而在目標尺度發生變化或被遮擋時， 算法跟蹤精度下降或目標丟失。 因此， 如何在目標形狀發生變化、? 翻轉或遮擋時依舊保持高精度跟蹤， 是運動目標跟蹤領域研究的熱點與難點。 軌跡預測法和目標分塊法可以有效提高環境變化時算法的適應性。 目標被局部遮擋或全部遮擋時， 軌跡預測法根據目標過去時刻運動狀態估計被遮擋時刻運動狀態， 有助于實現目標被短暫遮擋或全部遮擋時刻的穩健跟蹤[128]。 目標分塊法[129-130]對目標進行分塊， 由各個子塊的跟蹤結果得到總的目標位置， 可以準確處理目標被部分遮擋的情況。

（5） 提高穩定跟蹤的持久性

現有運動目標跟蹤算法多是針對短時跟蹤任務， 長時間目標跟蹤情況下， 魯棒性和跟蹤精度有下降趨勢， 因此， 確保長期魯棒的目標跟蹤算法值得進一步深入研究。 雖然已經有部分學者著手研究長時間的目標跟蹤， 但是缺乏長時間跟蹤算法框架， 算法本質是在短時間跟蹤算法框架下引入校正模塊或者加入重檢測模塊。 從根源上解決目標跟蹤的持久性與穩定性問題， 需要在長期跟蹤算法框架上進行探索與研究。

（6） 注重方法結構的繼承性

經典目標跟蹤算法積累深厚、? 計算簡捷、? 適應范圍廣， 將核學習方法嵌入到經典目標跟蹤方法框架， 有助于建立一般性算法架構， 提升算法靈活性與適用性， 便于算法評價。 如核學習方法中嵌入貝葉斯濾波等目標跟蹤算法， 可以提升目標短暫遮擋下的穩定跟蹤能力， 與置信傳播算法結合則有助于實現多個目標的有效跟蹤[51]。 因此， 注重實現核學習方法對經典目標跟蹤方法的繼承與融合， 對建立更具普適性的目標跟蹤算法具有顯著意義， 需要進一步探索與研究。

（7） 注重探測方法的兼容性

現有多數核學習方法是基于圖像和視頻處理的目標跟蹤算法， 在雷達目標跟蹤領域涉及較少。 實際上， 核學習方法有效提高了樣本空間內積化效率， 不僅適用于圖像視頻處理， 在基于雷達的有噪時間序列預測與估計、? 動力學模型建立等方面也有優良的性能[131-132]， 因此， 核學習方法有潛力擴展其應用范圍， 在雷達等非成像探測方式上實現兼具實時性和精準度的高性能目標跟蹤。

5 結 束 語

核學習方法作為線性到非線性之間的橋梁， 為許多模式分析應用領域提供了可行的統一框架。 將核方法應用于運動目標跟蹤， 通過核函數和核技巧簡化空間復雜的內積運算， 可在非線性處理、? 數據驅動、? 泛化性能等方面獲得較好表現。 基于核函數的目標跟蹤算法具有重要的研究意義和廣闊的應用前景， 在智能決策、? 無人系統、? 模式識別等領域具有潛在的應用價值。

參考文獻：

[1] Smeulders A W M，? Chu D M，? Cucchiara R，? et al. Visual Tracking：? An Experimental Survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，? 2014，? 36（7）：? 1442-1468.

[2] 王丹. 基于運動檢測的智能視頻監控系統設計[D]. 太原：? 中北大學，? 2017.

Wang Dan. Intelligent Video Surveillance System Design Based on Motion Detection[D]. Taiyuan：? North University of China，? 2017. （in Chinese）

[3] Gündüz G，? Acarman A T. A Lightweight Online Multiple Object Vehicle Tracking Method[C]∥ IEEE Intelligent Vehicles Symposium （IV），? 2018：? 427-432.

[4] 陸淵章，? 戴紅霞，? 胡瑩，? 等. 基于機器視覺的無人機協同目標跟蹤算法研究[J]. 電子器件，? 2020，? 43（5）：? 1096-1099.

Lu Yuanzhang，? Dai Hongxia，? Hu Ying，? et al. Research on Cooperative Target Tracking Algorithm for UAV Based on Machine Vision[J]. Chinese Journal of Electron Devices，? 2020，? 43（5）：? 1096-1099.（in Chinese）

[5] 高婷婷. 基于多目標跟蹤的醫學影像分析[D]. 西安：? 西安電子科技大學，? 2012.

Gao Tingting. Medical Image Analysis Based on Multi-Target Tracking[D]. Xian：? Xidian University，? 2012. （in Chinese）

[6] Aronszajn N. Theory of Reproducing Kernels[J]. Transactions of the American Mathematical Society，? 1950，? 68（3）：? 337.

[7] Schlkopf B，? Smola A，? Müller K R. Nonlinear Component Analysis as a Kernel Eigenvalue Problem[J]. Neural Computation，? 1998，? 10（5）：? 1299-1319.

[8] Mika S，? Ratsch G，? Weston J，? et al. Fisher Discriminant Analysis with Kernels[C]∥Neural Networks for Signal Processing IX：? Proceedings of the 1999 IEEE Signal Processing Society Workshop，? 1999：? 41-48.

[9] Bach F R，? Jordan M I. Kernel Independent Component Analysis[C]∥2003 IEEE International Conference on Acoustics，? Speech，? and Signal Processing，? 2003.

[10] Fukunaga K，? Hostetler L. The Estimation of the Gradient of a Density Function，? with Applications in Pattern Recognition[J]. IEEE Transactions on Information Theory，? 1975，? 21（1）：? 32-40.

[11] Cheng Y Z. Mean Shift，? Mode Seeking，? and Clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，? 1995，? 17（8）：? 790-799.

[12] Comaniciu D，? Ramesh V，? Meer P. Real-Time Tracking of Non-Rigid Objects Using Mean Shift[C]∥Proceedings IEEE Conference on Computer Vision and Pattern Recognition，? 2000：? 142-149.

[13] Comaniciu D，? Meer P. Mean Shift Analysis and Applications[C]∥Proceedings of the Seventh IEEE International Conference on Computer Vision，? 1999：? 1197-1203.

[14] Comaniciu D，? Meer P. Mean Shift：? A Robust Approach Toward Feature Space Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，? 2002，? 24（5）：? 603-619.

[15] Comaniciu D，? Meer P. Robust Analysis of Feature Spaces：? Color Image Segmentation[C]∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition，? 1997：? 750-755.

[16] Comaniciu D，? Ramesh V，? Meer P. The Variable Bandwidth Mean Shift and Data-Driven Scale Selection[C]∥Proceedings of the Eighth IEEE International Conference on Computer Vision，? 2001：? 438-445.

[17] Comaniciu D，? Ramesh V，? Meer P. Kernel-Based Object Tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，? 2003，? 25（5）：? 564-577.

[18] Lindeberg T. Feature Detection with Automatic Scale Selection[J]. International Journal of Computer Vision，? 1998，? 30（2）：? 79-116.

[19] Collins R T. Mean-Shift Blob Tracking through Scale Space[C]∥ IEEE Computer Society Conference on Computer Vision and Pattern Recognition，? 2003.

[20] 李鄉儒，? 吳福朝，? 胡占義. 均值漂移算法的收斂性[J]. 軟件學報，? 2005，? 16（3）：? 365-374.

Li Xiangru，? Wu Fuchao，? Hu Zhanyi. Convergence of a Mean Shift Algorithm[J]. Journal of Software，? 2005，? 16（3）：? 365-374.（in Chinese）

[21] Li X R，? Hu Z Y，? Wu F C. A Note on the Convergence of the Mean Shift[J]. Pattern Recognition，? 2007，? 40（6）：? 1756-1762.

[22] Birchfield S T，? Rangarajan S. Spatiograms Versus Histograms for Region-Based Tracking[C]∥ IEEE Computer Society Conference on Computer Vision and Pattern Recognition （CVPR），? 2005：? 1158-1163.

[23] 李培華. 一種改進的Mean Shift跟蹤算法[J]. 自動化學報，? 2007，? 33（4）：? 347-354.

Li Peihua. An Improved Mean Shift Algorithm for Object Tracking[J]. Acta Automatica Sinica，? 2007，? 33（4）：? 347-354.（in Chinese）

[24] 杜凱，? 巨永鋒，? 靳引利，? 等. 自適應分塊顏色直方圖的Mean Shift跟蹤算法[J]. 武漢理工大學學報，? 2012，? 34（6）：? 140-144.

Du Kai，? Ju Yongfeng，? Jin Yinli，? et al. Mean Shift Tracking Algorithm with Adaptive Block Color Histogram[J]. Journal of Wuhan University of Technology，? 2012，? 34（6）：? 140-144.（in Chinese）

[25] Gouiffès M，? Laguzet F，? Lacassagne L. Projection-Histograms for Mean-Shift Tracking[C]∥IEEE International Conference on Image Processing，? 2010.

[26] Leichter I，? Lindenbaum M，? Rivlin E. Mean Shift Tracking with Multiple Reference Color Histograms[J]. Computer Vision and Image Understanding，? 2010，? 114（3）：? 400-408.

[27] Leichter I. Mean Shift Trackers with Cross-Bin Metrics[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，? 2012，? 34（4）：? 695-706.

[28] Ning J，? Zhang L，? Zhang D，? et al. Robust Mean-Shift Tracking with Corrected Background-Weighted Histogram[J]. IET Computer Vision，? 2012，? 6（1）：? 62.

[29] Jeyakar J，? Babu R V，? Ramakrishnan K R. Robust Object Tracking with Background-Weighted Local Kernels[J]. Computer Vision and Image Understanding，? 2008，? 112（3）：? 296-309.

[30] Li L，? Feng Z P. An Efficient Object Tracking Method Based on Adaptive Nonparametric Approach[J]. Opto-Electronic Review，? 2005，? 13（4）：? 325-330.

[31] Allen J G，? Xu R Y D，? Jin J S. Mean Shift Object Tracking for a SIMD Computer[C]∥Third International Conference on Information Technology and Applications （ICITA），? 2005.

[32] Welch G. Bishop G. An Introduction to the Kalman Filter[R]. North Carolina： UNC-Chapel Hill，? 2006.

[33] 周尚波，? 胡鵬，? 柳玉炯. 基于改進Mean-Shift與自適應Kalman濾波的視頻目標跟蹤[J]. 計算機應用，? 2010，? 30（6）：? 1573-1576.

Zhou Shangbo，? Hu Peng，? Liu Yujiong. Target Tracking Based on Improved Mean-Shift and Adaptive Kalman Filter[J]. Journal of Computer Applications，? 2010，? 30（6）：? 1573-1576.（in Chinese）

[34] Babu R V，? Pérez P，? Bouthemy P. Robust Tracking with Motion Estimation and Local Kernel-Based Color Modeling[J]. Image and Vision Computing，? 2007，? 25（8）：? 1205-1216.

[35] Ali A，? Terada K. A General Framework for Multi-Human Tracking Using Kalman Filter and Fast Mean Shift Algorithms[J]. Journal of Universal Computer Science，? 2010，? 16（6）：? 921-937.

[36] Li X H，? Zhang T Y，? Shen X? D， et al. Object Tracking Using an Adaptive Kalman Filter Combined with Mean Shift[J]. Optical Engineering，? 2010，? 49（2）：? 020503.

[37] Chu C T，? Hwang J N，? Wang S Z，? et al. Human Tracking by Adaptive Kalman Filtering and Multiple Kernels Tracking with Projected Gradients[C]∥Fifth ACM/IEEE International Conference on Distributed Smart Cameras，? 2011：? 1-6.

[38] Chu C T，? Hwang J N，? Pai H I，? et al. Tracking Human under Occlusion Based on Adaptive Multiple Kernels with Projected Gra-dients[J]. IEEE Transactions on Multimedia，? 2013，? 15（7）：? 1602-1615.

[39] 彭寧嵩，? 楊杰，? 周大可，? 等. Mean-Shift跟蹤算法中目標模型的自適應更新[J]. 數據采集與處理，? 2005，? 20（2）：? 125-129.

Peng Ningsong，? Yang Jie，? Zhou Dake，? et al. Mean-Shift Tracking with Adaptive Model Update Mechanism[J]. Journal of Data Acquisition & Processing，? 2005，? 20（2）：? 125-129.（in Chinese）

[40] Peng N S，? Yang J，? Liu Z. Mean Shift Blob Tracking with Kernel Histogram Filtering and Hypothesis Testing[J]. Pattern Recognition Letters，? 2005，? 26（5）：? 605-614.

[41] Wang L L，? Xin Y H. A Small IR Target Detection and Tracking Algorithm Based on Morphological and Genetic-Particle Filter[J]. Acta Photonica Sinica，? 2013，? 42（7）：? 849-856.

[42] 魏坤，? 趙永強，? 潘泉，? 等. 基于均值漂移和粒子濾波的紅外目標跟蹤[J]. 光電子·激光，? 2008，? 19（2）：? 213-217.

Wei Kun，? Zhao Yongqiang，? Pan Quan，? et al. IR Target Tracking Based on Mean Shift and Particle Filter[J]. Journal of Optoelectronics Laser，? 2008，? 19（2）：? 213-217.（in Chinese）

[43] 張一帆，? 田雁， 楊帆， 等. 基于改進的Mean-Shift算法的紅外小目標跟蹤[J].紅處與激光工程，? 2014， 43（7）： 2164-2169.

Zhang Yifan，? Tian Yan，? Yang Fan，? et al. Infrared Dim Target Tracking Based on Improved Mean-Shift[J]. Infrared and Laser Engineering，? 2014， 43（7）： 2164-2169. （in Chinese）

[44] Zhang H H，? Huang Z Y，? Huang W M，? et al. Kernel-Based Method for Tracking Objects with Rotation and Translation[C]∥Proceedings of the 17th International Conference on Pattern Recognition，? 2004：? 728-731.

[45] Zhang H H，? Huang W M，? Huang Z Y，? et al. Affine Object Tracking with Kernel-Based Spatial-Color Representation[C]∥IEEE Computer Society Conference on Computer Vision and Pattern Recognition （CVPR），? 2005.

[46] Yilmaz A. Object Tracking by Asymmetric Kernel Mean Shift with Automatic Scale and Orientation Selection[C]∥IEEE Conference on Computer Vision and Pattern Recognition，? 2007.

[47] Yang C J，? Duraiswami R，? Davis L. Efficient Mean-Shift Tracking via a New Similarity Measure[C]∥IEEE Computer Society Conference on Computer Vision and Pattern Recognition（CVPR），? 2005.

[48] Elgammal A，? Duraiswami R，? Davis L S. Probabilistic Tracking in Joint Feature-Spatial Spaces[C]∥IEEE Computer Society Conference on Computer Vision and Pattern Recognition，? 2003.

[49] Elgammal A，? Duraiswami R，? Davis L S. Efficient Non-Parametric Adaptive Color Modeling Using Fast Gauss Transform[C]∥IEEE Computer Society Conference on Computer Vision and Pattern Re-cognition，? 2001.

[50] Leichter I，? Lindenbaum M，? Rivlin E. Visual Tracking by Affine Kernel Fitting Using Color and Object Boundary[C]∥? IEEE 11th International Conference on Computer Vision，? 2007.

[51] Park M，? Liu Y X，? Collins R T. Efficient Mean Shift Belief Propagation for Vision Tracking[C]∥ IEEE Conference on Computer Vision and Pattern Recognition，? 2008.

[52] Fan Z M，? Yang M，? Wu Y. Multiple Collaborative Kernel Tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，? 2007，? 29 （7）：? 1268-1273.

[53] Topkaya I S，? Erdogan H. Using Spatial Overlap Ratio of Independent Classifiers for Likelihood Map Fusion in Mean-Shift Tracking[J]. Signal，? Image and Video Processing，? 2019，? 13（1）：? 61-67.

[54] Wang H，? Wang X Y，? Yu L J，? et al. Design of Mean Shift Tracking Algorithm Based on Target Position Prediction[C]∥ IEEE International Conference on Mechatronics and Automation （ICMA），? 2019：? 1114-1119.

[55] Yu W S，? Hou Z Q，? Hu D，? et al. Robust Mean Shift Tracking Based on Refined Appearance Model and Online Update[J]. Multimedia Tools and Applications，? 2017，? 76（8）：? 10973-10990.

[56] Zeng H Q，? Chen J，? Cui X L，? et al. Quad Binary Pattern and Its Application in Mean-Shift Tracking[J]. Neurocomputing，? 2016，? 217：? 3-10.

[57] Phadke G，? Velmurugan R. Mean LBP and Modified Fuzzy C-Means Weighted Hybrid Feature for Illumination Invariant Mean-Shift Tracking[J]. Signal，? Image and Video Processing，? 2017，? 11（4）：? 665-672.

[58] Liu Y，? Jing X Y，? Nie J H，? et al. Context-Aware Three-Dimensional Mean-Shift with Occlusion Handling for Robust Object Tracking in RGB-D Videos[J]. IEEE Transactions on Multimedia，? 2019，? 21（3）：? 664-677.

[59] Bolme D S，? Beveridge J R，? Draper B A，? et al. Visual Object Tracking Using Adaptive Correlation Filters[C]∥ IEEE Computer Society Conference on Computer Vision and Pattern Recognition，? 2010：? 2544-2550.

[60] Henriques J F，? Caseiro R，? Martins P，? et al. Exploiting the Circulant Structure of Tracking-by-Detection with Kernels[C]∥12th? European Conference on Computer Vision， 2012： 702-715.

[61] Danelljan M，? Khan F S，? Felsberg M，? et al. Adaptive Color Attri-butes for Real-Time Visual Tracking[C]∥ IEEE Conference on Computer Vision and Pattern Recognition，? 2014：? 1090-1097.

[62] Henriques J F，? Caseiro R，? Martins P，? et al. High-Speed Tracking with Kernelized Correlation Filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，? 2015，? 37（3）：? 583-596.

[63] 何秀麗. 多元線性模型與嶺回歸分析[D]. 武漢：? 華中科技大學，? 2005.

He Xiuli. Research on Multivariate Linear Model and Ridge Regression[D]. Wuhan：? Huazhong University of Science and Technology，? 2005. （in Chinese）

[64] 王耀林，? 蓋夢歐，? 周敏. IMM算法在空中復雜機動目標跟蹤中的應用[J]. 現代信息科技，? 2020，? 4（13）：? 9-11.

Wang Yaolin，? Gai Mengou，? Zhou Min. Application of IMM Algorithm in Tracking Complex Maneuvering Targets in the Air[J]. Modern Information Technology，? 2020，? 4（13）：? 9-11.（in Chinese）

[65] Arulampalam M S，? Maskell S，? Gordon N，? et al. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking[J]. IEEE Transactions on Signal Processing，? 2002，? 50（2）：? 174-188.

[66] Kalal Z，? Mikolajczyk K，? Matas J. Tracking-Learning-Detection Kernel[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，? 2011，? 34（7）： 409-422.

[67] Zhang K H，? Zhang L，? Yang M H. Real-Time Compressive Tracking[C]∥12th European Conference on Computer Vision，? 2012：? 864-877.

[68] Danelljan M，? Hager G，? Khan F S，? et al. Accurate Scale Estimation for Robust Visual Tracking[C]∥British Machine Vision Conference，? 2014.

[69] Li Y，? Zhu J K. A Scale Adaptive Kernel Correlation Filter Tracker with Feature Integration[C]∥ European Conference on Computer Vision，?? 2015： 254-265.

[70] 王守義. 基于核相關濾波的目標跟蹤算法研究與實現[D]. 太原：? 中北大學，? 2018.

Wang Shouyi. Research and Implementation of Target Tracking Algorithm Based on Kernel Correlation Filtering[D]. Taiyuan：? North University of China，? 2018. （in Chinese）

[71] 張雷，? 王延杰，? 孫宏海，? 等. 采用核相關濾波器的自適應尺度目標跟蹤[J]. 光學精密工程，? 2016，? 24（2）：? 448-459.

Zhang Lei，? Wang Yanjie，? Sun Honghai，? et al. Adaptive Scale Object Tracking with Kernelized Correlation Filters[J]. Optics and Precision Engineering，? 2016，? 24（2）：? 448-459.（in Chinese）

[72] 秦曉飛，? 代順鋒，? 李峰. 基于改進的核相關濾波器的目標跟蹤算法[J]. 測控技術，? 2017，? 36（10）：? 3-6.

Qin Xiaofei，? Dai Shunfeng，? Li Feng. Target Tracking Algorithm Based on Improved Kernel Correlation Filter[J]. Measurement & Control Technology，? 2017，? 36（10）：? 3-6.（in Chinese）

[73] 錢堂慧，? 羅志清，? 李果家，? 等. 核相關濾波跟蹤算法的尺度自適應改進[J]. 計算機應用，? 2017，? 37（3）：? 811-816.

Qian Tanghui，? Luo Zhiqing，? Li Guojia，? et al. Scale Adaptive Improvement of Kernel Correlation Filter Tracking Algorithm[J]. Journal of Computer Applications，? 2017， ?37（3）：? 811-816.（in Chinese）

[74] 夏翔，? 張曉林，? 李嘉茂. 結合尺度預測的核相關濾波器目標跟蹤方法[J]. 電子設計工程，? 2017，? 25（2）：? 130-135.

Xia Xiang，? Zhang Xiaolin，? Li Jiamao. Kernelized Correlation Filter Based Visual Tracking with Scale Estimation[J]. Electronic Design Engineering，? 2017，? 25（2）：? 130-135.（in Chinese）

[75] Hannuna S，? Camplani M，? Hall J，? et al. DS-KCF：? A Real-Time Tracker for RGB-D Data[J]. Journal of Real-Time Image Processing，? 2019，? 16（5）：? 1439-1458.

[76] 劉延飛，? 何燕輝，? 姜柯，? 等. 采用異常值檢測及重定位改進的KCF跟蹤算法[J]. 計算機工程與應用，? 2018，? 54（20）：? 166-171.

Liu Yanfei，? He Yanhui，? Jiang Ke，? et al. Improved KCF Tracking Algorithm Using Outlier Detection and Relocation[J]. Computer Engineering and Applications，? 2018，? 54（20）：? 166-171.（in Chinese）

[77] Danelljan M，? Hger G，? Khan F S，? et al. Learning Spatially Regularized Correlation Filters for Visual Tracking[C]∥ IEEE International Conference on Computer Vision （ICCV），? 2015.

[78] 阮宏剛. 基于核相關濾波的目標跟蹤方法研究[D]. 南京：? 南京郵電大學，? 2018.

Ruan Honggang. Research on Object Tracking Based on Kernel Correlation Filter[D]. Nanjing：? Nanjing University of Posts and Telecommunications，? 2018. （in Chinese）

[79] Asha C S，? Narasimhadhan A V. Adaptive Learning Rate for Visual Tracking Using Correlation Filters[J]. Procedia Computer Science，? 2016，? 89：? 614-622.

[80] 陳智，? 柳培忠，? 駱炎民，? 等. 自適應特征融合的多尺度相關濾波目標跟蹤算法[J]. 計算機輔助設計與圖形學學報，? 2018，? 30（11）：? 2063-2073.

Chen Zhi，? Liu Peizhong，? Luo Yanmin，? et al. Multi-Scale Correlation Filter Tracking Algorithm Based on Adaptive Feature Fusion[J]. Journal of Computer-Aided Design & Computer Graphics，? 2018，? 30（11）：? 2063-2073.（in Chinese）

[81] Wang M M，? Liu Y，? Huang Z Y. Large Margin Object Tracking with Circulant Feature Maps[C]∥ IEEE Conference on Computer Vision and Pattern Recognition （CVPR），? 2017.

[82] Tang M，? Feng J Y. Multi-Kernel Correlation Filter for Visual Tracking[C]∥IEEE International Conference on Computer Vision （ICCV），? 2015.

[83] Huang B，? Xu T F，? Jiang S W，? et al. Robust Visual Tracking via Constrained Multi-Kernel Correlation Filters[J]. IEEE Transactions on Multimedia，? 2020，? 22（11）：? 2820-2832.

[84] 陳晨， 高艷麗， 鄧趙紅， 等. TSK模糊邏輯系統相關濾波器跟蹤算法[J]. 計算機科學與探索，? 2020， 14（2）：? 294-306.

Chen C，? Gao Y L，? Deng Z H，? et al. Correlation Filter Tracking Algorithm Using TSK Fuzzy Logic System[J]. Journal of Frontiers of Computer Science and Technology，? 2020， 14（2）：? 294-306. （in Chinese）

[85] Zhou Y，? Wang T，? Hu R H，? et al. Multiple Kernelized Correlation Filters （MKCF） for Extended Object Tracking Using X-Band Marine Radar Data[J]. IEEE Transactions on Signal Processing，? 2019，? 67（14）：? 3676-3688.

[86] 鄧春華，? 劉小楠，? 朱子奇，? 等. 一種基于時空顯著性的雙核KCF目標跟蹤方法：? CN110322479A[P]. 2019-10-11.

Deng Chunhua，? Liu Xiaonan，? Zhu Ziqi，? et al. Dual-Core KCF Target Tracking Method Based on Space-Time Significance：? CN110322479A[P]. 2019-10-11.（in Chinese）

[87] 王海軍， ?葛紅娟，? 張圣燕. 基于核協同表示的快速目標跟蹤算法[J]. 浙江大學學報： 工學版，? 2017，? 51（2）：? 399-407.

Wang Haijun，? Ge Hongjuan，? Zhang Shengyan. Fast Object Tracking Algorithm via Kernel Collaborative Presentation[J]. Journal of Zhejiang University： Engineering Science，? 2017，? 51（2）：? 399-407.（in Chinese）

[88] Battistone F，? Petrosino A，? Santopietro V. Best Structured Tracker[C]∥Workshop on Visual Object Tracking Challenge，? 2014.

[89] Montero A S，? Lang J，? Laganière R. Scalable Kernel Correlation Filter with Sparse Feature Integration[C]∥ IEEE International Conference on Computer Vision Workshop （ICCVW），? 2015.

[90] 鄭武興，? 王春平，? 付強，? 等. 融合灰度與顯著性特征的空中紅外目標跟蹤[J]. 激光與紅外，? 2018，? 48（3）：? 338-342.

Zheng Wuxing，? Wang Chunping，? Fu Qiang，? et al. Aerial Infrared Target Tracking Based on Gray and Saliency Features Fusion[J]. Laser & Infrared，? 2018，? 48（3）：? 338-342.（in Chinese）

[91] Lewis D P，? Jebara T，? Noble W S. Nonstationary Kernel Combination[C]∥The 23rd International Conference on Machine Learning，? 2006：? 553-560.

[92] Ong C S，? Smola A J，? Williamson R C. Learning the Kernel with Hyperkernels[J]. Journal of Machine Learning Research，? 2005，? 6：? 1043-1047.

[93] Lanckriet G，? Cristianini N，? Bartlett P，? et al. Learning the Kernel Matrix with Semi-Definite Programming[J]. Journal of Machine Learning Research，? 2002， 5： 323-330.

[94] Bach F R，? Lanckriet G R G，? Jordan M I. Multiple Kernel Learning，? Conic Duality，? and the SMO Algorithm[C]∥? The 21st International Conference on Machine Learning，? 2004：? 41-48.

[95] Sonnenburg S，? Ratsch G，? Schafer C. A General and Efficient Multiple Kernel Learning Algorithm[C]∥ The Advances in Neural Information Processing Systems，? 2005：? 1273-1280.

[96] Zien A，? Ong C S. Multiclass Multiple Kernel Learning[C]∥24th International Conference on Machine Learning，? 2007：? 1191-1198.

[97] Gehler P V，? Nowozin S. Infinite Kernel Learning[C]∥ Max Planck Institute for Biological Cybernetics，??? 2008.

[98] Gnen M，? Alpaydin E. Localized Multiple Kernel Learning[C]∥25th International Conference on Machine Learning，? 2008：? 352-359.

[99] Gnen M，? Alpaydin E. Multiple Kernel Learning Algorithms[J]. Journal of Machine Learning Research，? 2011，? 12：? 2211-2268.

[100] Lanckriet G R G，? Cristianini N，? Bartlett P，? et al. Learning the Kernel Matrix with Semidefinite Programming[J]. Journal of Machine Learning Research，? 2004，? 5：? 27-72.

[101] Lee W J，? Verzakov S，? Duin R P W. Kernel Combination Versus Classifier Combination[C] ∥7th International Workshop on Multiple Classifier Systems，? 2007：? 22-31.

[102] Pavlidis P，? Weston J，? Cai J，? et al. Gene Functional Classification from Heterogeneous Data[C]∥5th Annual International Conference on Computation Biology，? 2001：? 249-255.

[103] Lampert C H，? Blaschko M B. A Multiple Kernel Learning Approach to Joint Multi-Class Object Detection[C]∥DAGM： Joint Pattern Recognition Symposium，?? 2008：? 31-40.

[104] He J F，? Chang S F，? Xie L X. Fast Kernel Learning for Spatial Pyramid Matching[C]∥ IEEE Conference on Computer Vision and Pattern Recognition，? 2008.

[105] Kumar A，? Sminchisescu C. Support Kernel Machines for Object Recognition[C]∥ IEEE 11th International Conference on Computer Vision，? 2007.

[106] Damoulas T，? Girolami M A. Pattern Recognition with a Bayesian Kernel Combination Machine[J]. Pattern Recognition Letters，? 2009，? 30（1）：? 46-54.

[107] Mak B，? Kwok J T，? Ho S. A Study of Various Composite Kernels for Kernel Eigenvoice Speaker Adaptation[C]∥IEEE International Conference on Acoustics，? Speech，? and Signal Processing，? 2004.

[108] Fu S Y，? Guo S Y，? Hou Z G，? et al. Multiple Kernel Learning from Sets of Partially Matching Image Features[C]∥19th International Conference on Pattern Recognition，? 2008.

[109] Zheng S，? Liu J，? Tian J W. An Efficient Star Acquisition Method Based on SVM with Mixtures of Kernels[J]. Pattern Recognition Letters，? 2005，? 26（2）：? 147-165.

[110] Fung G，? Dundar M，? Bi J B，? et al. A Fast Iterative Algorithm for Fisher Discriminant Using Heterogeneous Kernels[C]∥21st International Conference on Machine Learning，? 2004.

[111] Damoulas T，? Girolami M A. Combining Feature Spaces for Classification[J]. Pattern Recognition，? 2009，? 42（11）：? 2671-2683.

[112] Damoulas T，? Girolami M A. Pattern Recognition with a Bayesian Kernel Combination Machine[J]. Pattern Recognition Letters，? 2009，? 30（1）：? 46-54.

[113] Camps-Valls G，? Gomez-Chova L，? Munoz-Mari J，? et al. Compo-site Kernels for Hyperspectral Image Classification[J]. IEEE Geo-science and Remote Sensing Letters，? 2006，? 3（1）：? 93-97.

[114] Camps-Valls G，? Martinez-Ramon M，? Rojo-Alvarez J L，? et al. Nonlinear System Identification with Composite Relevance Vector Machines[J]. IEEE Signal Processing Letters，? 2007，? 14（4）：? 279-282.

[115] Kingsbury N，? Tay D B H，? Palaniswami M. Multi-Scale Kernel Methods for Classification[C]∥IEEE Workshop on Machine Learning for Signal Processing，? 2005.

[116] Zheng D N，? Wang J X，? Zhao Y N. Non-Flat Function Estimation with a Multi-Scale Support Vector Regression[J]. Neurocomputing，? 2006，? 70（1/2/3）：? 420-429.

[117] Yang Z，? Guo J，? Xu W R，? et al. Multi-Scale Support Vector Machine for Regression Estimation[C]∥ 3rd International Symposium on Neural Networks，?? 2006： 1030-1037.

[118] Opfer R. Multiscale Kernels[J]. Advances in Computational Mathematics，? 2006，? 25（4）：? 357-380.

[119] Zhou Y T，? Zhang T Y，? Li X H. Multi-Scale Gaussian Processes Model[J]. Journal of Electronics （China），? 2006，? 23（4）：? 618-622.

[120] Walder C，? Kim K I，? Schlkopf B. Sparse Multiscale Gaussian Process Regression[C]∥25th International Conference on Machine Learning，? 2008.

[121] Christoudias M，? Urtasun R，? Darrell T. Bayesian Localized Multiple Kernel Learning[R]. Berkeley：? University of California，? 2009.

[122] Zhu P P，? Chen B D，? Principe J C. Learning Nonlinear Generative Models of Time Series with a Kalman Filter in RKHS[J]. IEEE Transactions on Signal Processing，? 2014，? 62（1）：? 141-155.

[123] Danelljan M，? Robinson A，? Khan F S，? et al. Beyond Correlation Filters：? Learning Continuous Convolution Operators for Visual? Tracking[C]∥14th European Conference on Computer Vision， 2016： 472-488.

[124] Danelljan M，? Bhat G，? Khan F S，? et al. ECO：? Efficient Convolution Operators for Tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition （CVPR），? 2017.

[125] Bhat G，? Johnander J，? Danelljan M，? et al. Unveiling the Power of Deep Tracking[C]∥15th European Conference on Computer Vision，? 2018：? 493-509.

[126] An X W，? Liang Q Q，? Sun N L. Multi-Kernel Support Correlation Filters with Temporal Filtering Constraint for Object Tracking[J]. Multimedia Tools and Applications， ?2021，? 80（9）：? 14041-14073.

[127] Su Z Y，? Li J，? Chang J， et al. Real-Time Visual Tracking Using Complementary Kernel Support Correlation Filters[J]. Frontiers of Computer Sciece，? 2020， 14（2）：? 417-429.

[128] Sun J P，? Ding E J，? Sun B，? et al. Adaptive Kernel Correlation Filter Tracking Algorithm in Complex Scenes[J]. IEEE Access，? 2020，? 8：? 208179-208194.

[129] Luo M Q，? Zhou B，? Wang T. Multi-Part and Scale Adaptive Visual Tracker Based on Kernel Correlation Filter[J]. PLoS One，? 2020，? 15（4）：? e0231087.

[130] Du F，? Wang W L，? Zhang Z. Target Tracking Algorithm for Pedestrians Movement Based on Kernel-Correlation Filtering[J]. Enterprise Information Systems，? 2020：? 1-15.

[131] Dang L J，? Chen B D，? Wang S Y，? et al. Kernel Kalman Filtering with Conditional Embedding and Maximum Correntropy Criterion[J]. IEEE Transactions on Circuits and Systems I：? Regular Papers，? 2019，? 66（11）：? 4265-4277.

[132] Rosinha J B，? de Almeida S J M，? Bermudez J C M. A New Kernel Kalman Filter Algorithm for Estimating Time-Varying Nonlinear Systems[C]∥ IEEE International Symposium on Circuits and Systems （ISCAS），? 2017：? 1-4.

A Review on Kernel Learning Method of Moving Target Tracking

Lou Jiaxin1， Li Yuankai1*， Wang Yuan1， Xu Yanke2

（1. University of Electronic Science and Technology of China， Chengdu 611731， China;

2. China Airborne Missile Academy， Luoyang 471009， China）

Abstract：? The kernel method maps the original spatial data to a high-dimensional Hilbert space by nonlinear mapping and hides the mapping in the linear learner. The kernel function is used to replace the complex inner product operation in high-dimensional space，? which can effectively avoid the ‘curse of dimensionality caused by high-dimensional space calculation. The kernel method has the advantages of learnability，? efficient calculation，? linearization and good generalization performance，? which provides a new effective way to solve the problem of nonlinear target tracking. The traditional target tracking methods often use the tracking model to predict the current motion state of the target and ensure the accuracy and real-time tracking. The kernel method provides a general way of linearization and can be independent of the specific model with efficient computing. Introducing the kernel learning method into target tracking is expected to improve environmental adaptability. In this paper，?? based on the idea of kernel method，? the current research progress of kernel learning target tracking is presented，? including target detection method based on kernel learning，? generative and discriminative target tracking method，? and multi-kernel learning method with different kernel functions. Further research on kernel learning target tracking for kernel function optimization，? long-term tracking，? feature extraction and target occlusion are prospected.

Key words：? ?kernel learning method; nonlinear mapping; target detection; target tracking; multiple kernel learning; pattern recognition