應用卡爾曼濾波的有源頭靠噪聲控制策略

王磊, 陳克安, 胥健, 齊旺

(西北工業大學 航海學院, 陜西 西安 710072)

區別于傳統的無源噪聲控制,有源噪聲控制(active noise control,ANC)利用聲波的相消性干涉,主要在低頻范圍發揮作用[1]。一般情況下,人們采用局部空間降噪代替全局降噪以降低系統復雜度,這樣只需要在人耳附近獲得降噪效果即可,因此有源頭靠技術有著重要的實際價值[2]。

為了能夠在人耳附近形成靜區又不影響人的活動,誤差傳聲器通常會放置在離人頭較遠的位置。為了在人耳處形成靜區,主要的辦法就是采用虛擬誤差傳感技術[3-6],這樣就可以在以虛擬誤差傳聲器為中心的較小空間內形成降噪區域。利用遠程傳聲器技術(remote microphone technique,RMT),事先測量初級聲場中物理誤差傳聲器與虛擬誤差傳聲器間的傳遞函數,以物理誤差傳聲器處的聲場估計虛擬誤差傳聲器處的聲場,從而實現虛擬誤差點的有源噪聲控制[7]。Kestell在自由場中利用前向差分預測外推多項式估計虛擬誤差點的聲壓[8]。Diaz在火車車廂模型的ANC系統中使用虛擬誤差傳感使得人耳附近達到15 dBA的降噪量[9]。Petersen等利用卡爾曼濾波(Kalman filter,KF)準確估計出虛擬誤差點的聲壓,從而在較寬的范圍內達到降噪效果[10]。雖然以上文獻采取的誤差傳感策略不盡相同,但是它們在ANC控制過程中均采用FxLMS算法,在收斂速度和穩態誤差等方面存在限制。

KF是基于狀態空間的算法。Lopes在單通道ANC系統中采用KF算法,比FxLMS和FxRLS算法獲得更多的降噪量[11],在此基礎上,將ANC系統的狀態空間描述為簡單的隨機游走模型,獲得了更加穩定的KF求解方法[12]。Ophem等將KF算法的應用擴展到多通道ANC系統,對參考信號進行平移,采用快速陣列算法降低了運算量[13]。Liebich等基于濾波器系數推導了新的狀態轉移矩陣代替簡單的隨機游走模型,進一步提升了收斂速度[14]。總的來說,KF算法以增加運算量為代價,提升了ANC系統的降噪性能,但其在算法穩定性上仍然存在一些問題。

本文針對虛擬誤差點的噪聲控制問題,采用KF算法提升系統的收斂速度和穩態誤差。首先算法狀態變量只包含控制濾波器系數,從根本上降低了KF的運算負擔。為了進一步降低算法的運算量,采用快速陣列算法。KF中的參數對算法性能有著決定性的影響,進一步對算法進行改進,給出了過程噪聲協方差矩陣Q1和測量噪聲協方差矩陣Q2的估計方法,保證了濾波結果的收斂。最后與FxLMS算法進行比較,通過仿真驗證提出算法的有效性及穩定性。

1 基于RMT的ANC系統

如圖1所示的有源降噪頭靠通常包含次級聲源、物理誤差傳聲器和虛擬誤差傳聲器。物理誤差傳聲器布置在距離人頭較遠的位置,虛擬誤差傳聲器布置在人耳位置。實際的自適應有源控制過程包括預辨識階段和控制階段。在預辨識階段估計初級聲場中物理誤差傳聲器與虛擬誤差傳聲器間的傳遞函數和次級通路傳遞函數。虛擬誤差傳聲器只在預辨識階段放置,控制階段通過物理誤差傳聲器的聲壓估計該處的聲壓。

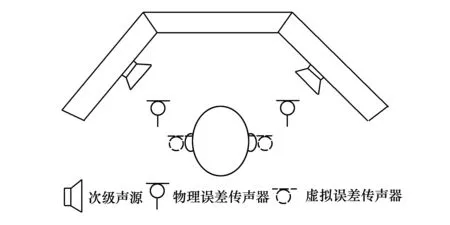
圖1 有源頭靠示意圖

通過虛擬誤差傳感技術將局部靜區從物理誤差傳聲器位置處移至虛擬誤差點位置。為了實現靜區的傳遞,采用RMT的ANC系統如圖2所示。

圖2 基于RMT的ANC系統

物理誤差傳聲器處的實際誤差信號ep(n)為初級信號dp(n)與次級聲源在誤差點形成的抵消信號s(n)的疊加

ep(n)=dp(n)+s(n)

(1)

則其初級信號的估計為

(2)

式中,y(n)為控制濾波器輸出的次級信號

y(n)=x(n)*w(n)

(3)

進而可以獲得虛擬誤差點處的誤差信號估計

(4)

通過LMS算法原理,利用濾波-x信號與估計的誤差信號對控制濾波器權系數w(n)進行更新,有

(5)

式中:μ為步長參數;rv(n)為參考信號x(n)經過次級通路濾波之后的濾波-x信號

(6)

由于迭代過程中使用的誤差信號為虛擬誤差點位置處的誤差信號估計，則控制系統將在虛擬誤差點取得降噪效果，系統性能將會受到估計準確性的影響。

2 基于KF的有源控制算法

2.1 算法描述

LMS算法對特征值擴散度具有較高的敏感性,可能導致較慢的收斂速度[15]。由于具有良好的過程參數估計,KF在收斂速度和魯棒性方面往往優于大多數自適應算法,KF算法引入了系統的狀態空間模型和狀態變量等概念。基于KF的有源頭靠虛擬誤差點噪聲控制系統如圖3所示。

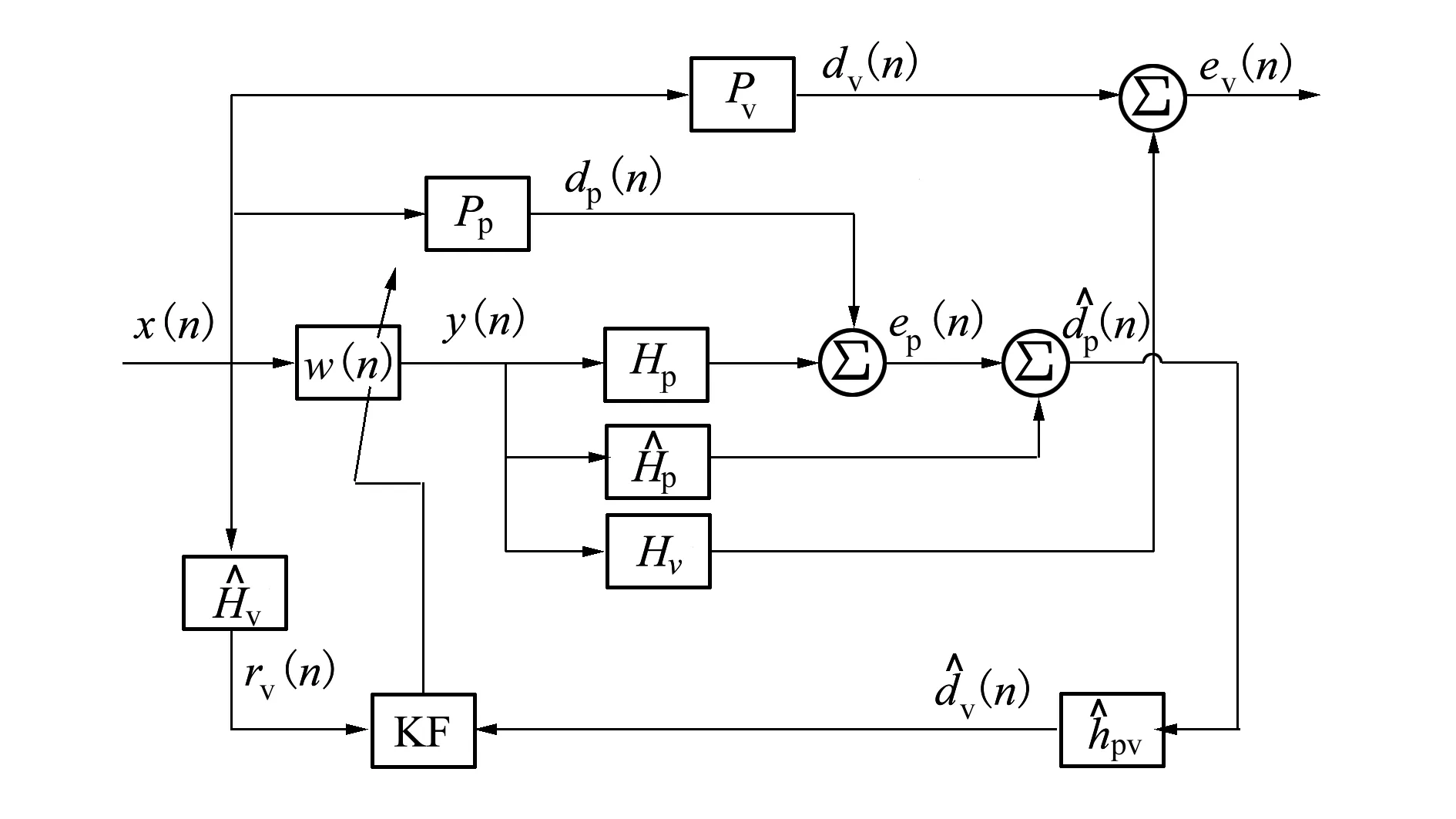
圖3 基于KF的虛擬誤差點ANC系統

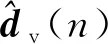
(7)

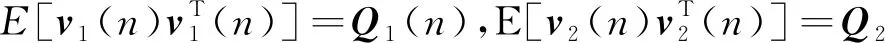
式中：I為參考傳聲器個數；J為次級聲源個數；L為控制濾波器階數；Kv為虛擬誤差點個數。

則應用于虛擬誤差點噪聲控制的多通道KF算法可以如下表示

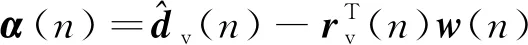
(10)

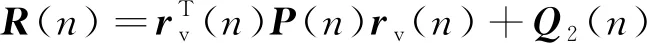
(11)

Kk(n)=F(n)P(n)rv(n)

(12)

P(n+1)=F(n)P(n)FT(n)-

(13)

w(n+1)=F(n)w(n)+Kk(n)R-1(n)α(n)

(14)

式中，P(n)為狀態估計誤差的相關矩陣。即

P(n)=E[w0(n)-w(n)][w0(n)-w(n)]T

(15)

表1中總結了描述有源頭靠噪聲控制的KF算法中用到的變量。

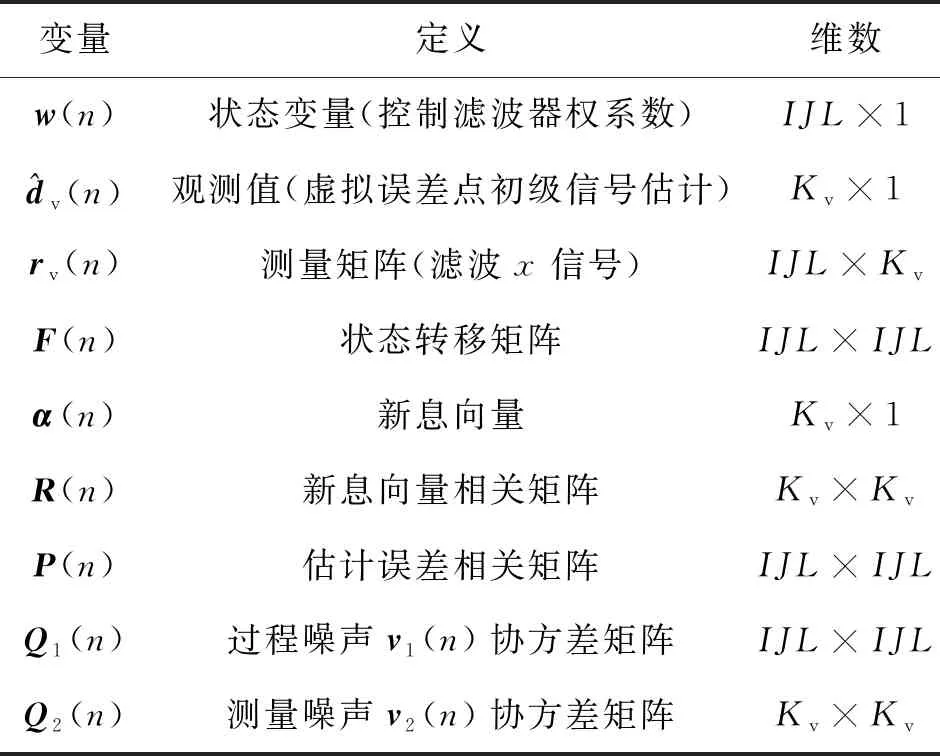
表1 卡爾曼變量小結

假設系統為隨機游走模型,狀態轉移矩陣選為單位矩陣,即F(n)=IIJL。KF算法以增加運算量為代價,提高了系統的收斂速度和降噪效果。以單位采樣時間內算法所需的乘法運算次數作為運算量,基于KF的有源頭靠降噪系統的運算量為

(16)

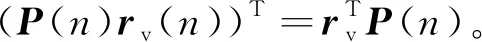
2.2 狀態噪聲估計

在上述模型中,已經假設整個ANC系統是線性的,且過程噪聲與測量噪聲皆為白噪聲。參數Q1(n)表示過程噪聲協方差,描述系統模型的不確定性,Q2(n)表示測量噪聲協方差,描述測量的不確定性。在實際情況中,Q1(n)和Q2(n)都是不能直接觀測的。針對建模不精確的問題,為了保證算法收斂,利用可觀測數據對過程噪聲和測量噪聲進行實時估計調整。

Q1(n)可以表示為

(17)

有

(18)

由(14)式可得

(19)

以時間平均代替集平均

(20)

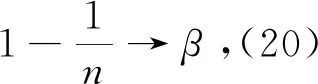
(21)

式中，0?β≤1。

測量噪聲協方差為

Q2(n)=diag{E[α(n)αT(n)]}

(22)

同樣地,有

Q2(n)=βQ2(n-1)+(1-β)diag{α(n)αT(n)}

(23)

(21)式和(23)式給出了過程噪聲與測量噪聲協方差矩陣的實時更新策略,當參數選取不當時,利用該策略可以在一定程度上避免濾波發散。

2.3 快速陣列算法

為了降低算法的運算量,采用快速陣列算法,利用Chandrasekhar遞歸代替Riccati方程[16]。此時控制濾波器權系數改寫為

(24)

狀態估計誤差的相關矩陣

(25)

該系統的狀態空間方程為

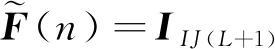
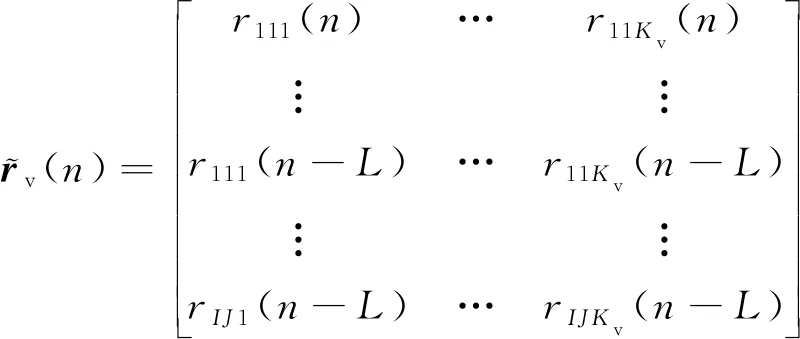
(27)

則有

(28)

式中

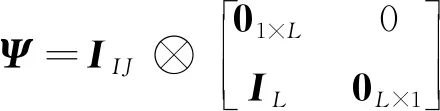
(29)

Δ=

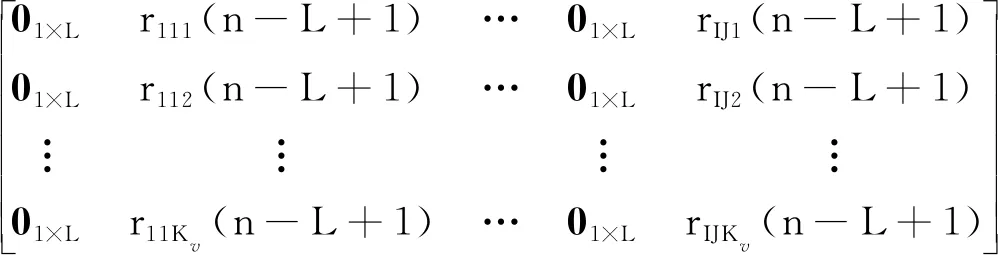
(30)

(11)～(13)式可以改寫為

L(n-1)M(n-1)LT(n-1)

(34)

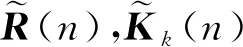
(35)

通過(35)式在后陣列中形成零矩陣塊,其中Θ為酉矩陣,滿足

Θ(n-1)J(n-1)ΘT(n-1)=J(n-1)

(36)

式中

J(n-1)=IK?M(n-1)

(37)

由(25)式可得

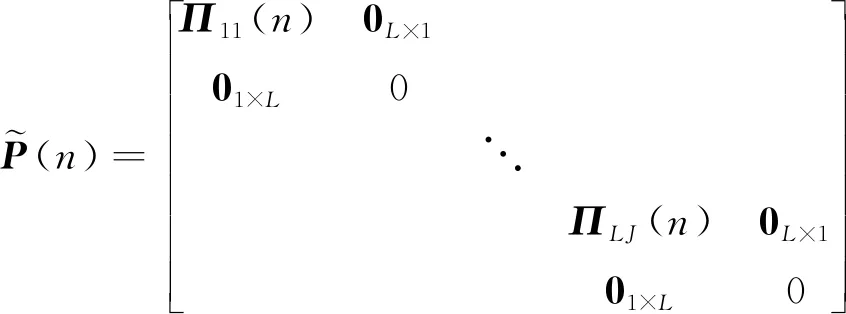
(38)

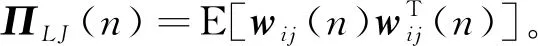
(39)

同理可得

(40)

則控制濾波器權系數的迭代為

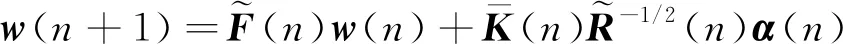
(41)

式中

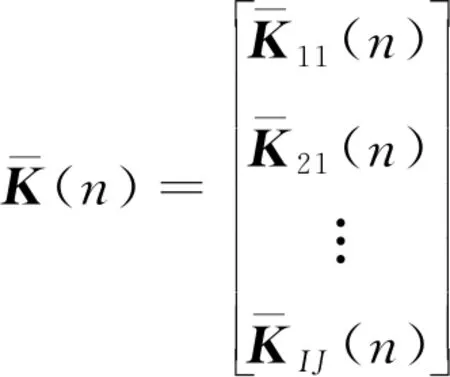
(42)

(10)、(35)和(41)式構成了多通道KF快速陣列算法,其運算量為

(43)

由(16)式和(43)式可以看出,KF快速陣列算法的運算量遠遠小于KF算法的運算量。如果ANC系統中I=1,J=Kp=Kv=2,M=N=128,L=256,則基于KF的有源頭靠系統運算量為10 567 68次乘法,而快速陣列算法的運算量為24 720次乘法。

3 仿真與討論

為了驗證所提算法的性能,在初級噪聲為寬帶噪聲的情況下,將提出的算法與基于FxLMS算法的有源頭靠系統進行了比較。仿真數據來自普通房間中的實測有源頭靠數據。系統中所含電聲器件個數為I=1,J=Kp=Kv=2。初級聲源位于人工頭后方,虛擬誤差傳聲器位于人工頭耳內部,次級聲源、物理誤差傳聲器和虛擬誤差傳聲器位于同一高度處。采樣頻率為fs=2 000 Hz。

3.1 系統預辨識

在ANC開始工作之前,首先對初級聲場中物理誤差傳聲器與虛擬誤差傳聲器之間的傳遞函數及次級通路脈沖響應進行辨識,建模濾波器皆為FIR濾波器,階數M=N=256。首先由初級聲源發聲,物理傳聲器與虛擬傳聲器接收聲壓信號,從而獲得它們之間的傳遞函數,建模結果如圖4所示。從圖中可以看出,利用物理誤差傳聲器處的初級信號可以大致估計出虛擬誤差傳聲器處的初級信號。

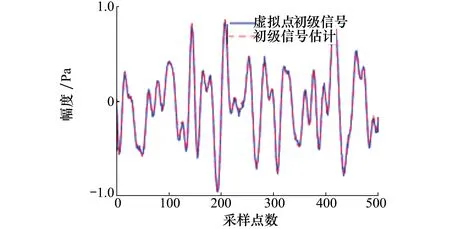
圖4 虛擬誤差點初級信號估計

然后由次級聲源發聲,獲得次級通路模型。圖5給出了次級聲源J1分別到虛擬誤差傳聲器Kp1和虛擬誤差傳聲器Kv1之間的脈沖響應。由圖中可以看出,次級聲源到虛擬誤差傳聲器的時延大于到物理誤差傳聲器的時延。

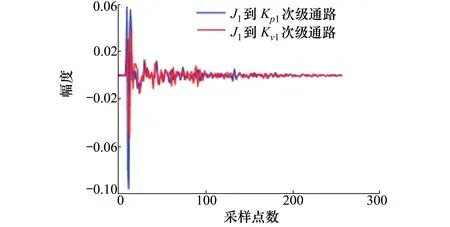
圖5 次級通路脈沖響應

3.2 降噪性能對比

ANC系統中通常使用傳聲器作為參考傳感器。在計算機仿真中,假設不存在聲反饋。分別利用FxLMS算法和KF算法對估計出來的虛擬誤差進行控制。控制濾波器階數選為L=512。為了評估不同算法的降噪性能,定義

(44)

在第一組仿真中,參考信號設為零均值的高斯白噪聲。將KF算法標為KF1,KF快速陣列算法標為KF2。通過試錯選擇算法的最佳參數,以獲得每種算法的最佳性能。FxLMS算法步長參數為μ=5.23×10-4;KF1中Q1=0,Q2=10-3I;KF2中Q1=0,Q2=3×10-3I,仿真結果如圖6所示。

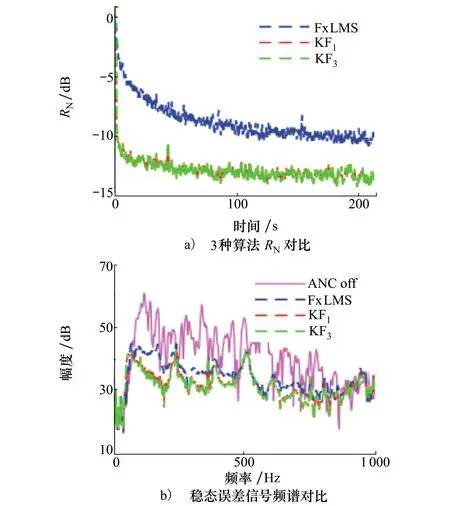
圖6 算法性能比較

圖6a)中給出了3種算法RN的對比,由圖6a)中可以看出,在算法開始階段,2種KF算法迅速收斂到較小的RN值。KF1算法和KF2算法能夠獲得近似的降噪效果。算法運行經過200 s后,FxLMS算法的RN值為-9.7 dB,KF1和KF2算法的RN值為-13.4 dB。第一個虛擬誤差點處的穩態誤差信號頻譜如圖6b)所示。3種算法的最終降噪效果近似,RN值分別為-11.3 dB,-14.1 dB和-14.2 dB。

為了使得KF算法有效,需要合理選擇算法中的協方差參數Q1和Q2,如果參數選擇不當,將無法達到好的降噪效果,甚至有可能引起濾波過程發散,這時,狀態噪聲估計的優勢得以顯示出來。隨機選擇2組Q1和Q2,KF3表示在KF1中進行狀態噪聲協方差估計。性能比較如圖7所示,圖7a)表現了全局對比,圖7b)細化了0.5 s以內的局部對比。由圖中可以看出,當Q1=Q2=10-6I,KF1在算法開始階段迅速發散,而KF3依舊能達到好的降噪效果,當Q1=10-8I,Q2=10-1I,KF1和KF3都能達到收斂,但是KF3有更快的收斂速度。由此可以看出噪聲估計策略可以在一定程度上保證算法快速收斂。

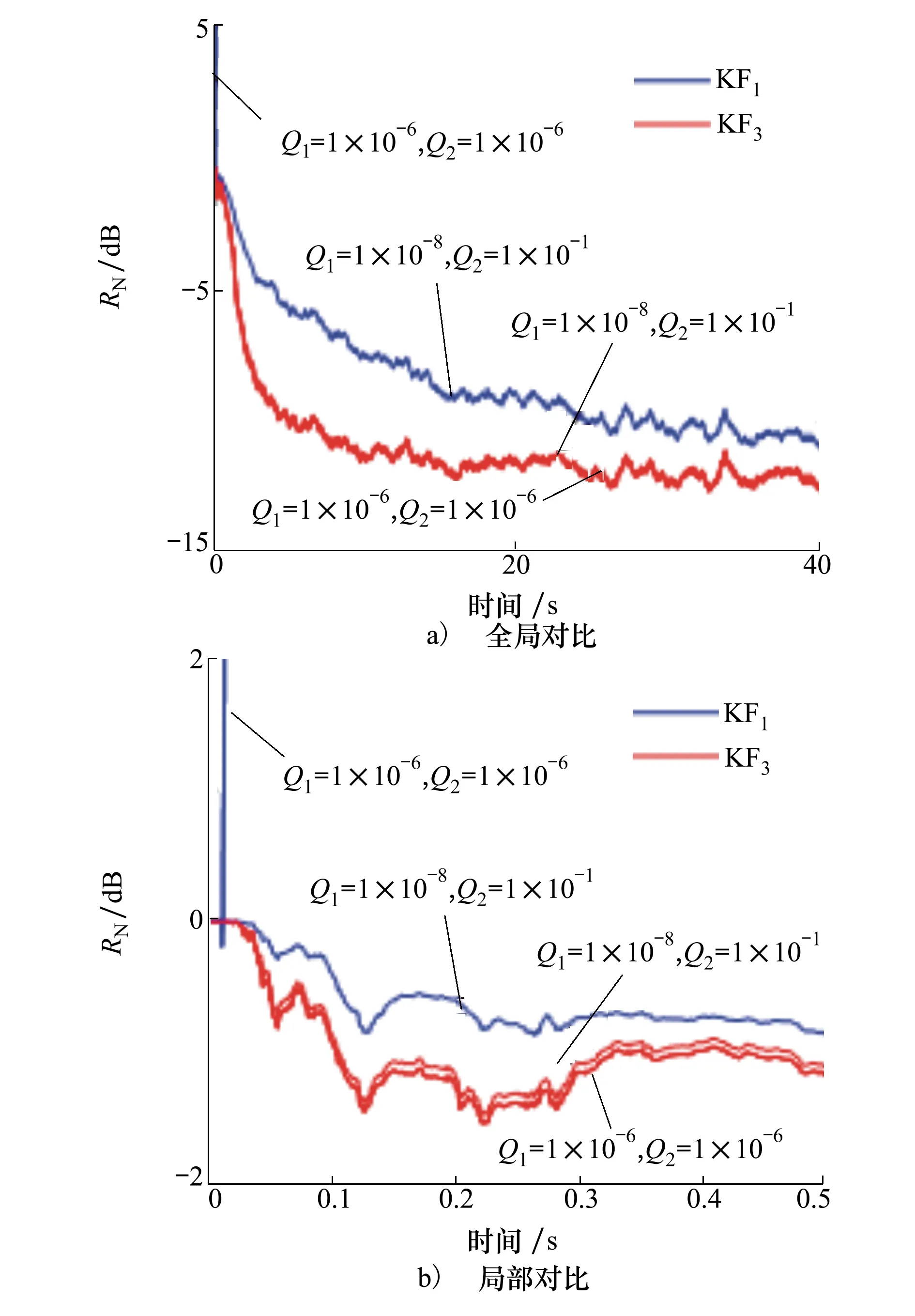
圖7 狀態噪聲估計性能對比

在第二組仿真中,設置106 s時初級信號d(n)幅度突然發生變化,變為原來的1/2。分別對KF1和KF3算法進行仿真,結果如圖8所示。圖8a)給出了算法的RN對比,第一個虛擬誤差點處的誤差信號時域圖如8b)所示。由圖中可以看出,當初級信號發生突變時,KF1算法收斂緩慢,KF3算法中誤差信號幅度迅速減小,收斂到較低的RN值。算法運行至200 s時, KF1和KF3算法的RN值分別為-5.1 dB和-14.2 dB。仿真結果表明,KF3算法能夠有效跟蹤系統的動態變化。

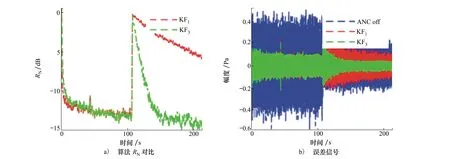
圖8 狀態噪聲估計性能對比

4 結 論

本文對有源頭靠中虛擬誤差點的有源降噪進行了研究,提出了基于KF的算法,建立了狀態空間方程。與FxLMS算法相比,基于KF的算法收斂速度更快,且收斂后的殘余噪聲更小。進一步地,為了保證算法收斂,提出了狀態空間噪聲協方差估計策略,在KF參數選擇不當時仍然能夠保證降噪效果,并且能夠跟蹤系統變化。引入快速陣列方法后降低了KF算法的運算量。仿真結果證明,提出的算法能夠獲得更好的性能。