小學數學應用題解法探析
孫東梅
在九年制義務教育中,小學是初始階段,是人生接受教育的開始,其內容應該是以后進一步學習的基礎。小學數學應該是數學中基礎的基礎,按理說難度不大。但是事實上并不這樣的,比如說數學中的應用題,其中的數量關系和問題就著實繁雜,有歸一問題,歸總問題,和差問題,和倍問題,差倍問題,行程問題,盈虧問題等。要想很好地駕馭這些問題,不是輕而易舉的,因為沒有一個通用的公式可以套用,沒有一個統一的解題過程,可以說生活有多豐富,應用題就有多精彩。下面介紹幾種我在長期的教學實踐過程中,總結的一些行之有效方法。
一、歸宗法
何為“歸宗法”,就是回歸真諦,回歸生活,正所謂萬變不離其宗,要想解決數學問題,就是從生活中來,再回到生活中去,就像百川歸海。眾所周知,數學來源于生活,以生活為基礎;反過來,學好數學又可以很好地解決實際生活中的問題。正因為如此,我們要想學好數學就不能脫離實際生活,應該深入生活,體察生活,只有這樣,才能不斷地從豐富多彩的生活中發現數學的存在和解決實際生活中的問題,學以致用;否則要想學好數學就變成了空中樓閣了。試想一個從未走出大山的農村兒童如何回答這樣的問題:用微波爐加熱一個蘋果大概需要多長時間?再如,一個生活在城市中的孩子能否回答這個問題:張爺爺買了一打蠟燭,用了4根,還有幾根?蠟燭是什么?一打是多少?結果可想而知。所以說,我們不能為了學習數學而學習數學,數學來之生活,更應回歸生活。不能站在岸上學游泳。我認為這是學好數學乃至學好任何學科的不二法門,也是許多同行忽視的地方。
二、轉換法
由于小學生的認知和心理發展特點的原因,他們接受事物習慣于客觀具體的,不習慣于主觀抽象的;并且,他們的知識遷移能力不強,對于題目中出現的自己熟悉的事物和概念比較容易接受,相反就很茫然。但是,我們的數學學習不能等到孩子們長大后才開始,這就要求我們教師要善于引導和啟發,把不熟悉的轉換成熟悉的,把復雜的轉換成簡單,把未知的轉換成已知的。比如說有這樣一題:一工程隊修一段1公里馬路,第一天修了一半,第二天修了剩下的一半,第三要修多遠才能修完?對于小學底年級的學生而言,修路的工程和進程未必熟悉,如果換成吃糖,方便面,巧克力,那他們幾乎就可以口算了。
例:一支毛筆的單價和10之鉛筆的價錢相同,買6支毛筆和20支鉛筆,一共花掉80元,毛筆和鉛筆的單價格式多少?
分析與解:有題可知,一直毛筆和10之鉛筆的價錢相同,所以把6之毛筆換成6 x 10 = 60(支)鉛筆,即買6之毛筆和20之鉛筆,一共花掉80元就轉化為買60之鉛筆盒20之鉛筆,一共花帶80元,從而可以得出每一支鉛筆的單價為80 ÷ (6 x 10+20)=1元,進而可以求出毛筆的單價為1x10=10元。
三、假設法
在教學或解題的過程中,因為條件不夠經常使人感到束手無策,就像過河無橋亦無舟,這是應該怎么辦?遇到這種我們不能一味硬解,可以另辟蹊徑,可以創造條件來幫助解決問題,這種方法可簡單地分為設未知數x和不設x,很常用也很好用。下面通過實例加以說明:
四、圖文法
應用題的出現大多以文字的形式,由于小學生的閱歷和理解能力的限制,字面內容和較為復雜的數量關系,容易給他們理解上帶來困難,如果理解不了題目的準確意思,那就很難解題了。為此,針對這種情況,我們可以引導學生將文字和圖畫結合起來,因為圖畫或圖表具有形象直觀的特點,便于學生理解和接受。
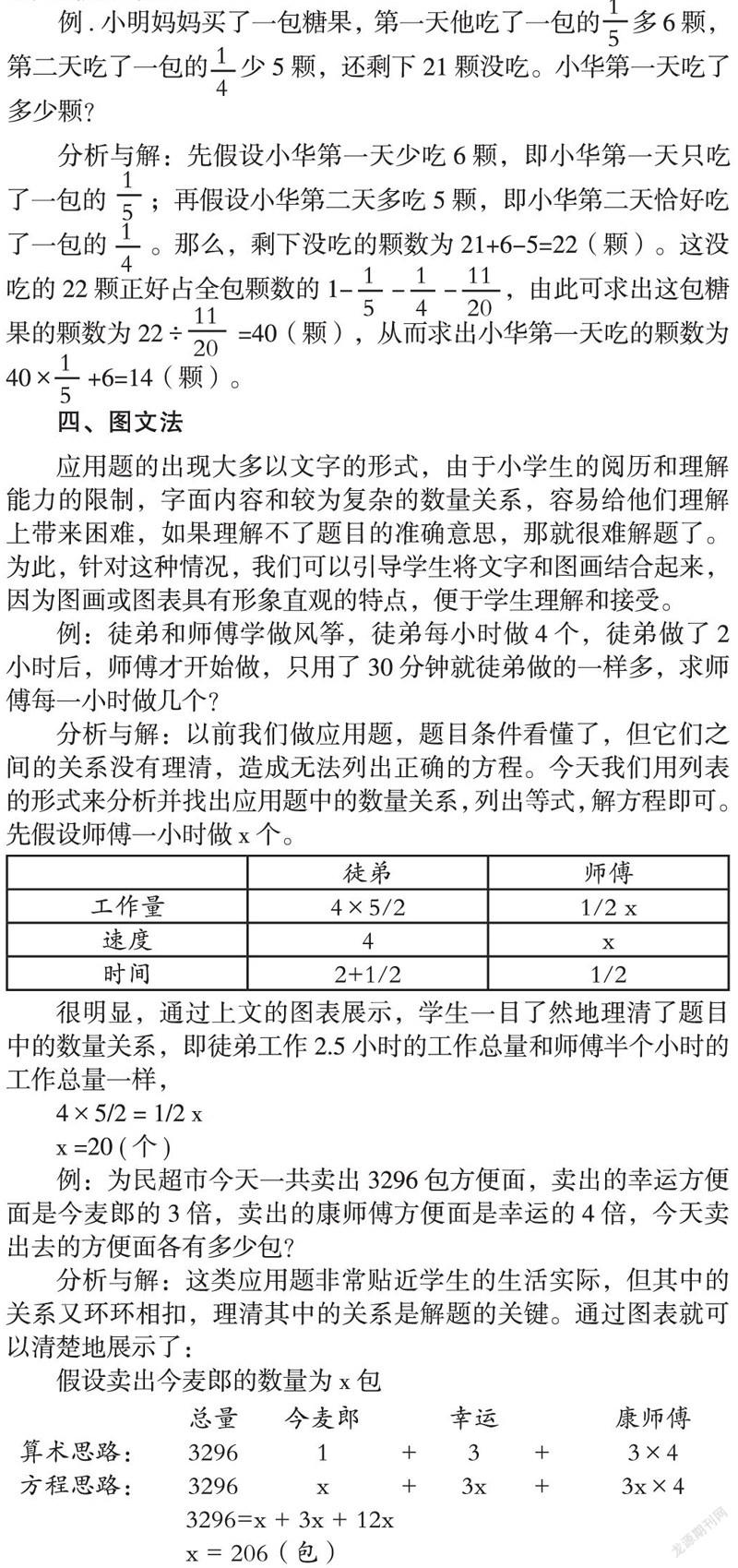
例:徒弟和師傅學做風箏,徒弟每小時做4個,徒弟做了2小時后,師傅才開始做,只用了30分鐘就徒弟做的一樣多,求師傅每一小時做幾個?
分析與解:以前我們做應用題,題目條件看懂了,但它們之間的關系沒有理清,造成無法列出正確的方程。今天我們用列表的形式來分析并找出應用題中的數量關系,列出等式,解方程即可。先假設師傅一小時做x 個。
很明顯,通過上文的圖表展示,學生一目了然地理清了題目中的數量關系,即徒弟工作2.5小時的工作總量和師傅半個小時的工作總量一樣,
例:為民超市今天一共賣出3296包方便面,賣出的幸運方便面是今麥郎的3倍,賣出的康師傅方便面是幸運的4倍,今天賣出去的方便面各有多少包?
分析與解:這類應用題非常貼近學生的生活實際,但其中的關系又環環相扣,理清其中的關系是解題的關鍵。通過圖表就可以清楚地展示了:
通過列表法解應用題主要是達到這樣兩個目的:一是培養學生的分析能力、歸納概括能力,提高解答應用題的效率和質量;二是指導學生系統地掌握各類應用題的特點,培養學生靈活的解題思路和方法。
小學數學應用題貫穿于小學數學教學的整個過程,而且,應用題所涉及的內容非常廣泛,所以,教育者要提高重視程度,適時靈活地轉換教學方法和策略。我們執教者不能只局限于解這些問題,更要注重通過解決這些問題達到培養學生的探索能力和思維能力,進而提升綜合素質。

