關(guān)于數(shù)列極限求法的探討*
劉喜富 王艷輝
(重慶師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院 重慶 401331)
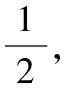
1.利用等價(jià)替換求極限

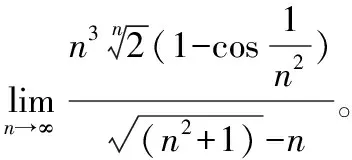
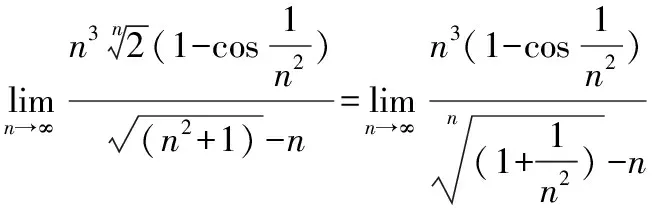
2.利用兩個(gè)重要極限求極限
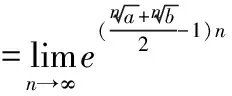
因此可得
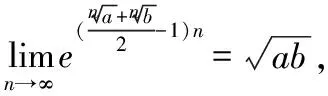
3.利用夾逼定理求極限
無法直接求數(shù)列極限時(shí),可以將數(shù)列適當(dāng)?shù)目s小和放大,使得縮小、放大后的數(shù)列易于求出其極限,且具有相同的極限值,則原數(shù)列極限存在,且等于二者的共同值。
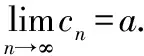
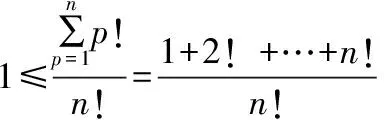
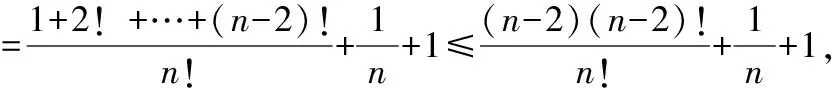
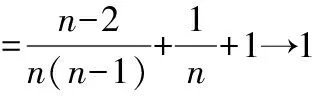
4.利用單調(diào)有界定理求極限
我們知道單調(diào)有界數(shù)列必有極限[1]。在運(yùn)用此定理時(shí),通常先根據(jù)數(shù)列的特點(diǎn),證明該數(shù)列是單調(diào)有界,然后假設(shè)其極限為a,然后通過解方程求出的值,且要注意根的取舍問題。
例4:證明下列數(shù)列極限存在,并求其極限值:設(shè)
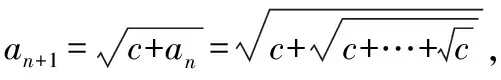

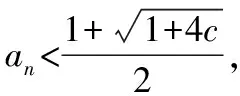
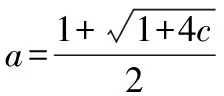
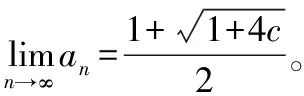
5.利用定積分定義求極限
當(dāng)遇到極限形式是和或者積的形式時(shí),先判定其是否可以化作某一個(gè)函數(shù)在某一區(qū)間上的積分和,如果可以,則原極限就可以轉(zhuǎn)化為計(jì)算一個(gè)定積分。
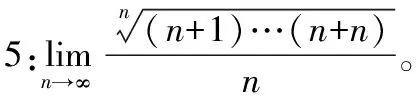
解:先化解極限式
根據(jù)定積分定義式,有
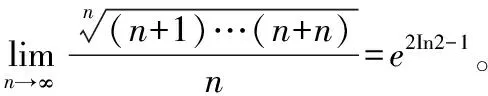
6.利用級(jí)數(shù)求極限
在求數(shù)列極限時(shí),有些數(shù)列可以通過判斷級(jí)數(shù)的收斂性,進(jìn)而來求通項(xiàng)的極限。
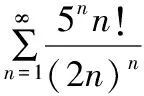
4.結(jié)束語
數(shù)列極限的求解方法有很多,通過對(duì)一些方法和技巧的整理,在做題時(shí),我們可以根據(jù)題目特點(diǎn),選擇合適的方法進(jìn)行求解。當(dāng)然,有時(shí)候一道題需要運(yùn)用多種方法進(jìn)行求解,除了一些基本的方法,特殊方法也是需要我們?nèi)タ紤]和篩選的,有時(shí)可能會(huì)達(dá)到意想不到的效果。因此,這就需要我們對(duì)各種方法的熟練和透徹的了解。

