空腔膨脹理論靶體阻力模型及其應(yīng)用研究進(jìn)展*
劉均偉,張先鋒,劉 闖,陳海華,熊 瑋,談夢婷
(南京理工大學(xué)機械工程學(xué)院,江蘇 南京 210094)
隨著固體動力學(xué)、彈塑性動力學(xué)、計算力學(xué)、材料力學(xué)以及數(shù)學(xué)分析工具的發(fā)展,人們不再滿足于實驗研究這種只能給出彈靶作用最終結(jié)果的研究方法。彈體侵徹過程最基本的問題是確定靶體對彈體的作用,即阻力函數(shù)。目前,應(yīng)用較多的研究方法有空腔膨脹模型[1-3]、局部相互作用理論[4]、微分面力法[5]、速度勢和速度場理論[6]、土盤模型[7-8]等。其中較為成熟且應(yīng)用廣泛的確定靶體阻力函數(shù)方法為空腔膨脹模型,該模型綜合考慮了靶體強度(由屈服準(zhǔn)則描述)、體積模量(由狀態(tài)方程描述)和密度等多種因素的影響,主要用于分析典型靶體材料在沖擊載荷下的破壞響應(yīng)特性,進(jìn)而確定靶體的抗侵徹阻力。學(xué)者們先后以柱形、球形空腔膨脹理論為基礎(chǔ),針對塑性、(準(zhǔn))脆性材料,取得了豐富的研究成果。準(zhǔn)靜態(tài)球形和柱形空腔膨脹模型的控制方程最早由Bishop 等[1]提出,并求解得到了錐形彈體低速侵徹金屬靶體的阻力。Bishop 等[1]和Hopkins[3]首次給出了動態(tài)空腔膨脹的控制方程,通過求解方程得到了不可壓縮理想彈塑性靶體對彈體的阻力。Hunter 等[9]首先假設(shè)材料的屈服應(yīng)力和密度之間的比值為常數(shù), 利用相似變換建立了可壓縮材料的動態(tài)球形空腔膨脹模型, 該研究開創(chuàng)了相似變換在空腔膨脹理論中應(yīng)用的先河,對空腔膨脹模型的發(fā)展應(yīng)用起到了重要的推動作用。空腔膨脹理論的發(fā)展與更新速度很快,其關(guān)鍵問題則集中于材料本構(gòu)關(guān)系和破壞準(zhǔn)則的修正,即將材料體積變形方程從不可壓縮向躍變壓縮、線性壓縮、非線性壓縮發(fā)展;強度模型則從理想彈塑性向線性硬化、冪次硬化、壓力相關(guān)強度準(zhǔn)則、分階段強度準(zhǔn)則過渡,并可考慮脆性斷裂效應(yīng),其發(fā)展路線圖如圖1 所示。
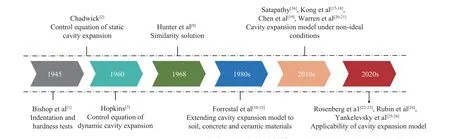
圖1 空腔膨脹模型發(fā)展路線圖[1-3,9-26]Fig. 1 The development circuit diagram of cavity expansion model[1-3,9-26]
Hopkins[3]全面總結(jié)了第二次世界大戰(zhàn)后關(guān)于空腔膨脹理論的相關(guān)研究工作。自此以后,學(xué)者們以空腔膨脹理論為基礎(chǔ),發(fā)展了可用于描述多種類靶體材料的阻力模型計算方法,較好地應(yīng)用于工程實際問題中,成為靶體阻力計算的重要手段。本文中主要介紹空腔膨脹模型的起源及理論體系、塑性及脆性材料的響應(yīng)分區(qū)、空腔徑向應(yīng)力的理論及數(shù)值求解方法、空腔膨脹模型在多個方向的應(yīng)用等,結(jié)合彈靶侵徹效應(yīng)發(fā)展特點給出空腔膨脹模型理論體系及應(yīng)用的未來研究方向。
1 空腔膨脹模型理論體系
相關(guān)研究工作表明,當(dāng)加載于材料上的載荷超過材料本身的屈服極限時,材料出現(xiàn)層次分明的不同響應(yīng)區(qū)。Collombet 等[27]、Curran 等[28]、Wei 等[29]分別開展了典型塑性及脆性材料在高速沖擊下的響應(yīng)特性研究,獲得了如圖2~3 所示的靶體破壞形式。這與彈體高速撞擊到裝甲上時,發(fā)散的球面波在裝甲內(nèi)傳播的情形類似;而在彈體侵徹靶體中的穩(wěn)定侵徹階段,靶體中的開孔與彈體侵徹形成的空腔類似。因此,靶體對彈體的抗侵徹阻力可以通過無限域介質(zhì)內(nèi)部空腔膨脹的壓力來模擬。

圖2 塑性材料破壞情況[29]Fig. 2 Failure of plastic material[29]
空腔膨脹模型的基本假設(shè)是:用空腔在無限大介質(zhì)中膨脹時所產(chǎn)生的表面徑向應(yīng)力,替代彈體侵徹過程中表面法向所受到的阻力。材料在空腔擴展下的響應(yīng)分區(qū)與材料自身動態(tài)力學(xué)特性相關(guān),塑性與脆性材料的空腔響應(yīng)及分區(qū)特點區(qū)別明顯,圖4 為響應(yīng)區(qū)示意圖,其中cc、cd、cp、ce分別為彈性區(qū)與開裂區(qū)、開裂區(qū)與粉碎區(qū)、彈性區(qū)與塑性區(qū)的界面?zhèn)鞑ニ俣燃皬椥圆úㄋ佟Mǔ饘俨牧隙技俣涨粩U展會在靶體內(nèi)產(chǎn)生彈性-塑性響應(yīng)分區(qū)[30]。對脆性材料而言,當(dāng)膨脹速度較低時,空腔擴展會在靶體內(nèi)形成彈性-開裂-粉碎響應(yīng)分區(qū);當(dāng)膨脹速度較高時,則為彈性-粉碎響應(yīng)分區(qū)[31]。
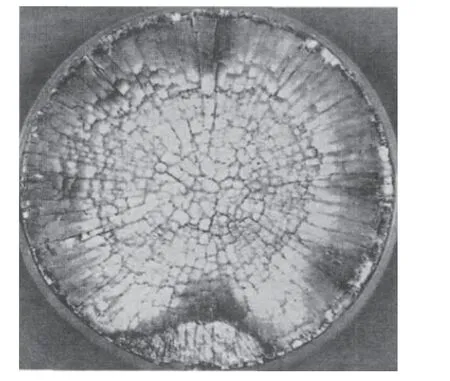
圖3 脆性材料破壞情況[27]Fig. 3 Failure of brittle material[27]
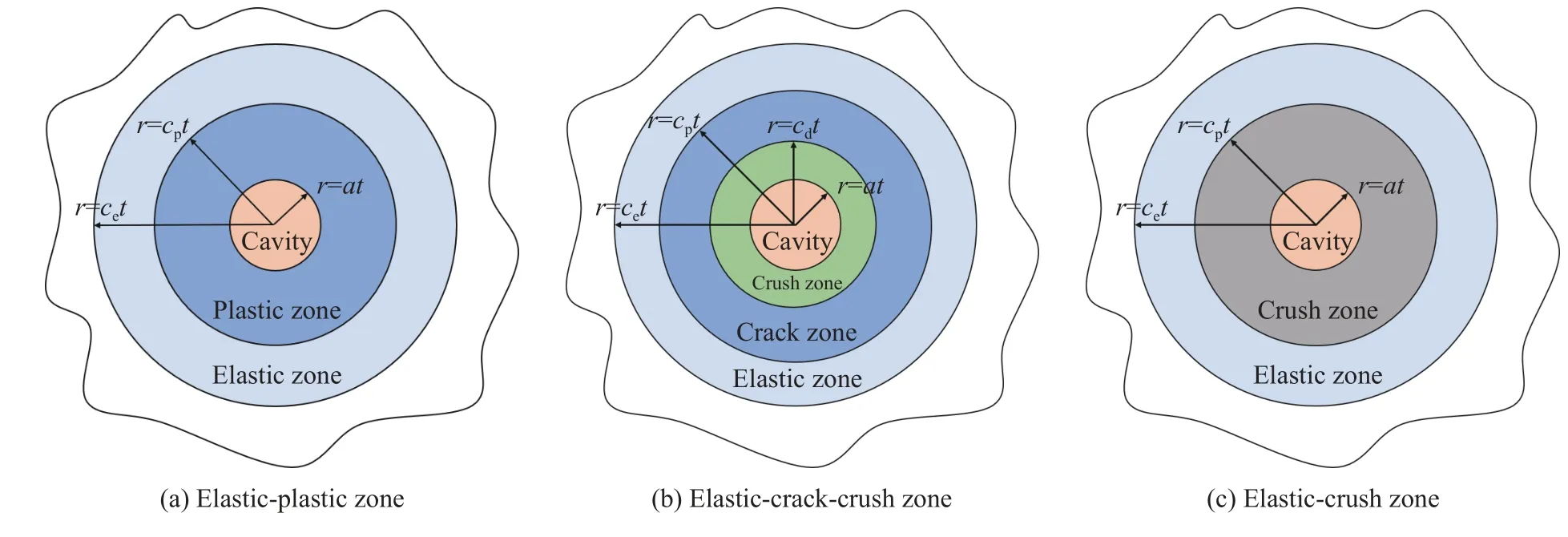
圖4 響應(yīng)區(qū)示意圖Fig. 4 Schematic diagram of response area
空腔膨脹模型的求解一般是從質(zhì)量和動量守恒方程出發(fā),并根據(jù)連續(xù)介質(zhì)力學(xué)的基本原理以及材料的本構(gòu)方程來推導(dǎo)空腔表面徑向應(yīng)力的大小,所得結(jié)果一般可以表示為空腔膨脹速度的二次函數(shù)形式[32]。根據(jù)模型假定不同,空腔膨脹模型分為球形/柱形空腔膨脹,球形和柱形[32-33]空腔膨脹理論適用于不同的研究對象,兩種模型對不同彈體頭部形狀的計算精度不同。一般而言,在球、柱坐標(biāo)系下,靶板介質(zhì)的質(zhì)量和動量守恒方程分別為:

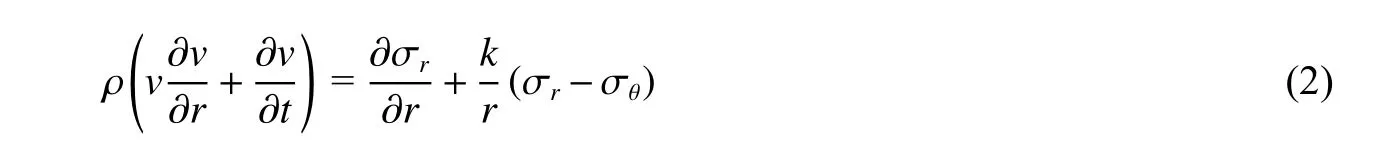
式中:v為質(zhì)點速度,r為徑向坐標(biāo), σr、 σθ分別為徑向、環(huán)向應(yīng)力, ρ 為材料密度;當(dāng)k=1 時,為柱坐標(biāo)系;當(dāng)k=2 時,為球坐標(biāo)系。
空腔膨脹模型的基本方程包括守恒方程和材料的本構(gòu)方程,可結(jié)合邊界條件、初始條件和波陣面間斷條件或彈塑性邊界的連續(xù)性條件等求解。邊界條件一般為位移邊界條件和應(yīng)力邊界條件,空腔壁處質(zhì)點位移等于空腔半徑ura=ra以及空腔外側(cè)邊界處徑向應(yīng)力σre=σ(t) ,其中 σ (t)=0 時為自由邊界。各響應(yīng)分區(qū)的交界面滿足Hugoniot 跳躍條件,質(zhì)量守恒、動量守恒形式的Hugoniot 跳躍條件為:
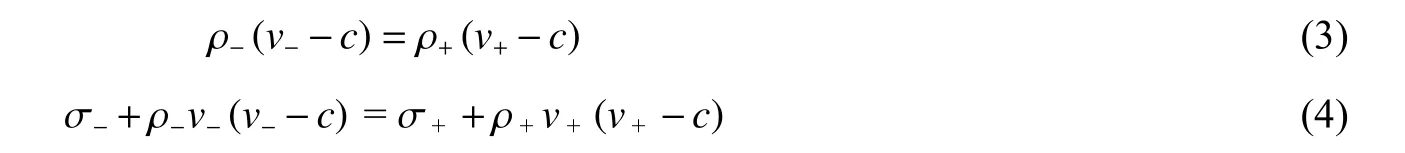
式中:c為波陣面速度,下標(biāo)+、-分別代表波前、波后介質(zhì)狀態(tài)。
最理想化的模型為彈塑性不可壓縮材料的靜態(tài)空腔膨脹模型,模型假設(shè)在彈塑性材料的空腔邊界(r=r0) 處施加一個恒定載荷p0,并不考慮慣性作用和波動效應(yīng),當(dāng)載荷逐漸增加至臨界值、材料達(dá)到穩(wěn)定膨脹時,空腔邊界徑向應(yīng)力 σr則為材料靜阻力Rt。Bishop 等[1]、Hill 等[34]、Chadwick[2]、Hopkins[3]、Huang[35]和Forrestal 等[10]分別給出了靜態(tài)空腔膨脹解的幾個等效推導(dǎo),典型結(jié)果如下式:

式中:Y為材料的屈服強度,E為彈性模量。
靜態(tài)空腔膨脹模型未考慮材料的慣性效應(yīng),而當(dāng)膨脹速度較高時,慣性效應(yīng)對空腔徑向應(yīng)力計算結(jié)果的影響不可忽略。Hill[34]第一個給出了不可壓縮延性材料的動態(tài)空腔膨脹模型的解析解。通過假設(shè)材料不可壓縮并結(jié)合小變形假設(shè),得出彈塑性邊界c與空腔邊界a的關(guān)系為c(t)/a(t)=E/(1+ν)Y,空腔徑向應(yīng)力為:
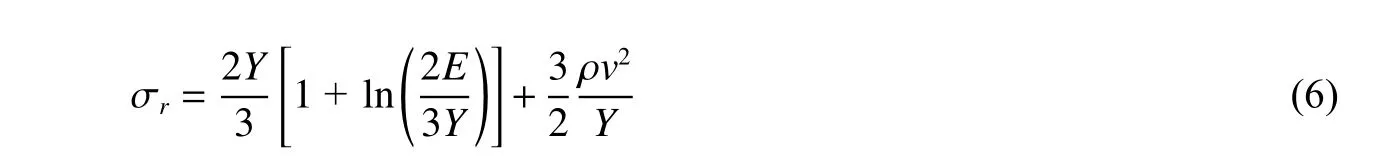
式中:第1 項為準(zhǔn)靜態(tài)項,與靜態(tài)空腔膨脹模型結(jié)果相同;第2 項為與速度相關(guān)的慣性項。
材料的不可壓縮假設(shè)有利于空腔膨脹模型解析解的求解,但正如Chadwick[2]和Hunter 等[9]所指出的,不可壓縮假設(shè)導(dǎo)致了彈性波速是無窮大的,且由于空腔膨脹速度與塑性波速具有恒定的比例,空腔膨脹速度不可能超越塑性波速,與實際情況不符。
Hunter 等[9]指出,對于以恒定速度擴張空腔的情況,由于侵徹過程主要是由穩(wěn)態(tài)侵徹部分控制,而穩(wěn)態(tài)侵徹具有自相似性,因此與穩(wěn)態(tài)侵徹相關(guān)的動態(tài)空腔膨脹也具有自相似性,可以采用相似變換求解,其中應(yīng)力、速度和密度取決于單個相似性變量。Hunter 等[9]假設(shè)在整個空腔擴展過程中,屈服應(yīng)力與密度之比是恒定的,研究結(jié)果表明,隨著空腔擴張速度的增加,彈塑性界面速度逐漸增加,并最終達(dá)到彈性波速度。
Forrestal 等[11]在Hunter 等[9]的基礎(chǔ)上,給出了以恒定速度擴展的可壓縮材料的動態(tài)空腔膨脹解決方案。通過使用Hugoniot 跳躍條件以及材料在彈塑性界面的任一側(cè)屈服的條件,F(xiàn)orrestal 等[11]計算得出粒子速度、徑向應(yīng)力在彈塑性邊界上是連續(xù)的,并引入了以下無量綱參數(shù):
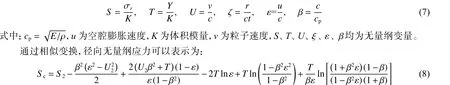
式中:S2和U2通過彈塑性邊界兩側(cè)應(yīng)力、位移連續(xù)得出,S2和U2由下式確定:

空腔膨脹模型理論體系是由基本假定、響應(yīng)模式、守恒方程、本構(gòu)模型(屈服準(zhǔn)則和狀態(tài)方程)和求解條件(邊界、界面和應(yīng)力波條件等)組成的完備體系。材料的穩(wěn)定響應(yīng)區(qū)劃分、屈服準(zhǔn)則、狀態(tài)方程、求解條件等影響因素不是割裂的,共同影響模型計算的空腔邊界徑向壓力 σr;當(dāng)采用不同假設(shè)條件時,相同材料參數(shù)計算出來的空腔徑向應(yīng)力也會有所差別。
2 理想侵徹條件的空腔膨脹壓力計算模型
Poncelet 公式是最古老和最經(jīng)典的計算平頭彈撞擊金屬靶侵徹阻力的公式:F=A0(a1+b1v2),其中A0是彈體的橫截面積,v是撞擊速度,a1、b1為實驗確定的材料常數(shù)。理想侵徹條件指具有一般凸形頭部形狀的剛性彈垂直侵徹半無限靶目標(biāo)[19],在考慮了彈形幾何因素后,理想侵徹條件下的空腔膨脹壓力計算模型[11]得到了與Poncelet 公式幾乎完全相同的侵徹阻力計算式,即侵徹阻力由靶體材料的靜強度項和流動阻力組成,動態(tài)空腔膨脹理論進(jìn)一步提供了Poncelet 公式的理論基礎(chǔ)。
自20 世紀(jì)80 年代以來,美國Sandia 國家實驗室Forrestal 團隊分別對球形和柱形動態(tài)空腔膨脹理論進(jìn)行了詳細(xì)的研究,同時進(jìn)行了大量侵徹實驗對其驗證。此后有關(guān)空腔膨脹的工作主要集中在:
(1)不同的靶體材料,如鋁合金[11-12]、混凝土[13,36-37]、土[10]、巖石[14-15]、沙子[38]和陶瓷[16]等;
(2)靶體塑性區(qū)屈服準(zhǔn)則,Tresca 屈服準(zhǔn)則[12-13]、Drucker-Prager 屈服準(zhǔn)則[37]、Mohr-Coulomb 屈服準(zhǔn)[14-15, 36, 38]等;
(3)塑性區(qū)狀態(tài)方程,線性靜水壓力-體應(yīng)變狀態(tài)方程[30,36]、線性鎖應(yīng)變模型[10,13]、三階段非線性狀態(tài)方程[37]以及p-α 狀態(tài)方程[38]等。
2.1 靶體材料
陳小偉等[19]和Forrestal 等[11-12]針對鋁合金材料,假定材料為冪應(yīng)變硬化、速率無關(guān)的彈塑性材料,建立了空腔初始半徑從零開始的動態(tài)膨脹模型,計算結(jié)果如圖5 所示。Forrestal 等[11-12]分析了可壓縮性對材料的影響,發(fā)現(xiàn)材料的不可壓縮假設(shè)會高估空腔阻力。Forrestal 等[30]借鑒金屬材料空腔膨脹理論,考慮混凝土的拉伸斷裂,將混凝土的響應(yīng)區(qū)分為塑性區(qū)-裂紋區(qū)-彈性區(qū)和塑性區(qū)-彈性區(qū)兩種模式,假設(shè)塑性區(qū)滿足Mohr-Coulomb 失效準(zhǔn)則,裂紋區(qū)的環(huán)向應(yīng)力為零,考慮不可壓縮和可壓縮線性壓力-應(yīng)變關(guān)系兩種情況,計算結(jié)果如圖6 所示。研究表明,響應(yīng)區(qū)劃分對塑性區(qū)應(yīng)力影響較大,在混凝土材料響應(yīng)區(qū)中加入裂紋區(qū)會降低空腔徑向應(yīng)力值;而不同的響應(yīng)區(qū)劃分下,彈性-裂紋區(qū)界面移動速度大于塑性-裂紋區(qū)界面移動速度。
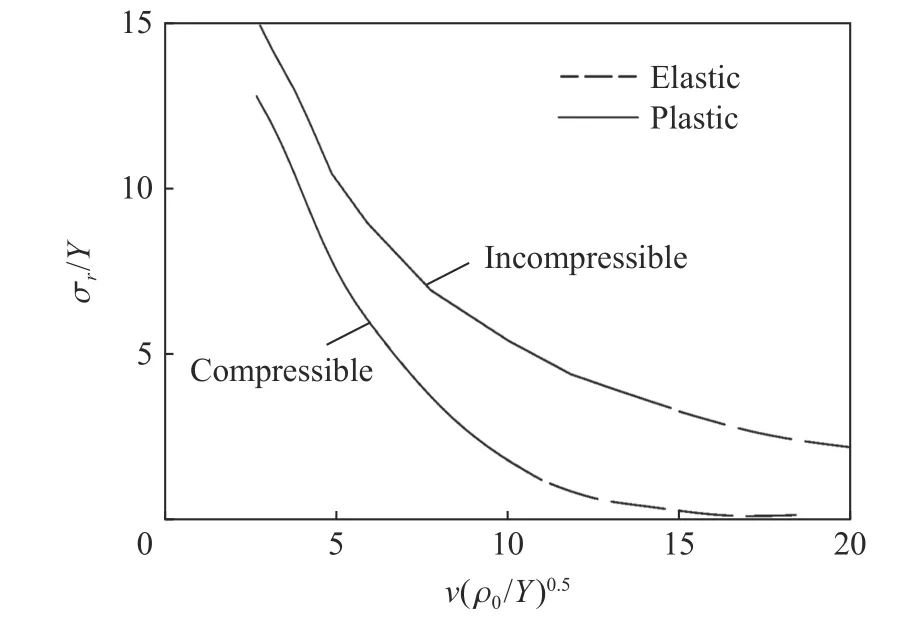
圖5 不同速度下的空腔徑向應(yīng)力分布[11-12]Fig. 5 Radial stress distribution of cavity atdifferentvelocity[11-12]
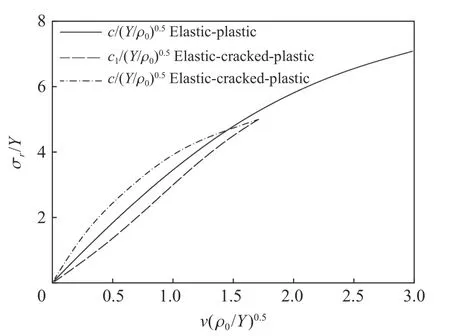
圖6 不同分區(qū)下界面移動速度[30]Fig. 6 Interface moving speed under different partitions[30]
與傳統(tǒng)混凝土相比,超高強度混凝土(ultra-high performance cement based composite,UHPCC)具有更加優(yōu)異的抗侵徹性能[17-18,39-43],對于高速彈體侵徹UHPCC 目標(biāo),彈體-目標(biāo)界面周圍的壓力可以達(dá)到數(shù)吉帕,其中壓力-體積應(yīng)變的關(guān)系表現(xiàn)出非線性特征,Kong 等[44]、Peng 等[45]引入了雙曲屈服準(zhǔn)則和非線性狀態(tài)方程來描述彈體侵徹下UHPCC 材料的塑性行為,提出了一種改進(jìn)的彈體侵徹UHPCC 的動態(tài)空腔膨脹模型。圖7~8 為有關(guān)屈服準(zhǔn)則和狀態(tài)方程的實驗數(shù)據(jù),從圖中可以看出,基于線性屈服準(zhǔn)則和EOS 的經(jīng)典空腔膨脹模型不適用于UHPCC,雙曲屈服準(zhǔn)則和非線性EOS 分別在擬合抗剪強度-壓力數(shù)據(jù)和壓力-體積應(yīng)變數(shù)據(jù)時更實用和靈活。

圖7 剪切強度-壓力數(shù)據(jù)和屈服準(zhǔn)則[44]Fig. 7 Shear strength-pressure data and yield criteria[44]

圖8 壓力體積應(yīng)變測試數(shù)據(jù)和狀態(tài)方程[44]Fig. 8 Pressure-volumetric strain tests data and EOS[44]
Satapathy[16]研究陶瓷材料以恒定速度打開球形空腔所需的壓力時發(fā)現(xiàn),隨著空腔膨脹速度逐漸增加,粉碎區(qū)邊界速度cp逐漸逼近并超過破裂區(qū)邊界速度cc,即破碎區(qū)消失,如圖9 所示。在很高的空腔膨脹速度下,粉碎區(qū)域的傳播速度會以略低于縱向波速的水平達(dá)到飽和[46]。
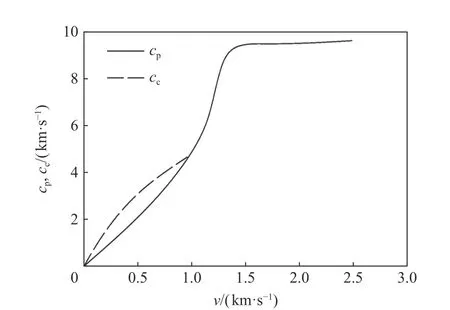
圖9 粉碎和破碎區(qū)域的速度[10]Fig. 9 Speeds of the comminuted and cracked zones[10]
Hunter 等[9]首先將空腔膨脹模型應(yīng)用于球形彈體對土介質(zhì)的侵徹問題。其后Hanagud 等[47]將其推廣至可壓縮介質(zhì)中,Norwood[48]則采用柱形空腔膨脹理論求解了土介質(zhì)的侵徹問題。Forrestal等[10]將土壤的壓力-體積應(yīng)變理想化為線性關(guān)系,采用Morh-Coulomb 和Tresca 屈服準(zhǔn)則描述塑性區(qū),推導(dǎo)了不同剪切強度模型的球形空腔膨脹問題的方程,計算結(jié)果如圖10 所示。Forrestal 等[10]的研究表明,不同屈服準(zhǔn)則對空腔徑向應(yīng)力有較大影響,隨著 λ 的增加,空腔表面徑向應(yīng)力逐漸增大,實際應(yīng)用中應(yīng)合理選擇描述材料屈服行為的準(zhǔn)則。
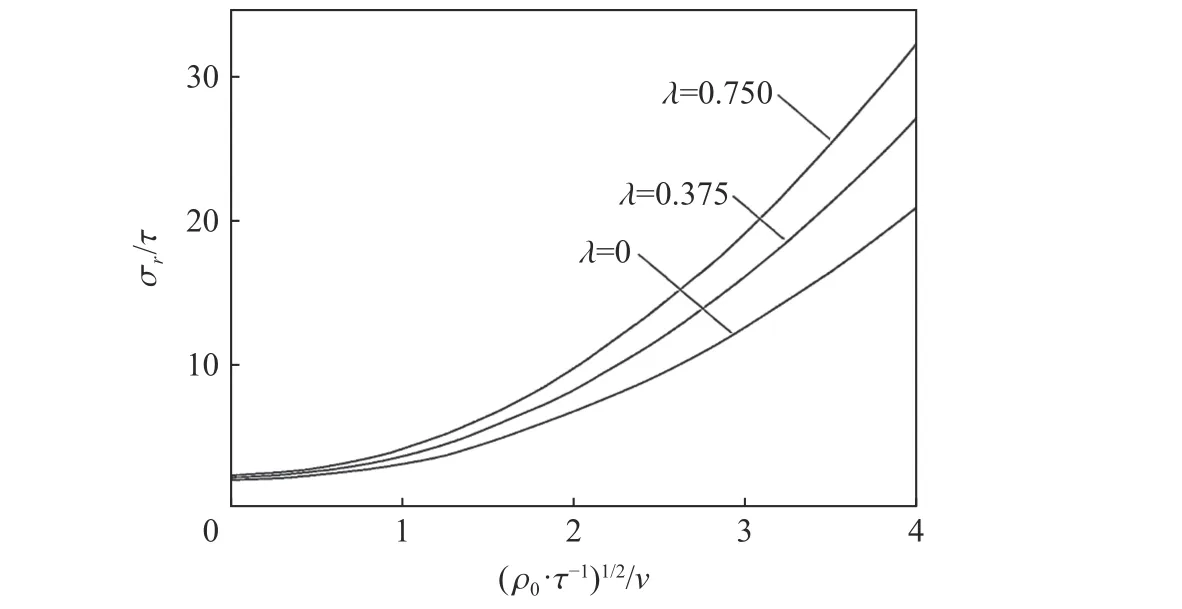
圖10 不同屈服準(zhǔn)則下徑向應(yīng)力與速度的關(guān)系[10]Fig. 10 The relationship between radial stress and velocity under different yield criteria[10]
Shi 等[38]采用p-α 狀態(tài)狀態(tài)方程和Mohr-Coulomb-Tresca 極限屈服準(zhǔn)則來描述砂土的本構(gòu)關(guān)系,建立了考慮砂土可壓縮性的球形空腔膨脹模型,圖11~12 為空腔速度與空腔徑向應(yīng)力、彈塑性界面移動速度的關(guān)系,結(jié)果表明,對于含孔隙的砂土類材料,忽略可壓縮性將高估空腔徑向壓力。Satapathy[16]在Bless 等[49]工作的基礎(chǔ)上,將響應(yīng)區(qū)劃分為空腔-粉碎-徑向裂紋-彈性-無擾動,假設(shè)粉碎區(qū)材料滿足Morh-Coulomb 屈服準(zhǔn)則,模型預(yù)測的結(jié)果與實驗[50]吻合程度較好。
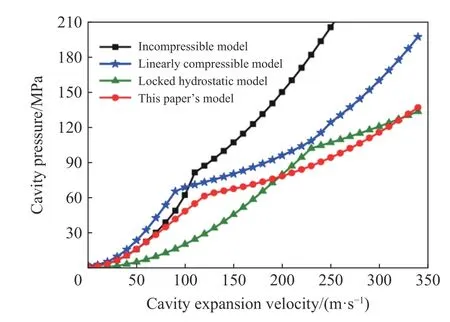
圖11 空腔徑向應(yīng)力與空腔速度的關(guān)系[38]Fig. 11 The relation between cavity radial pressure and cavity velocity[38]
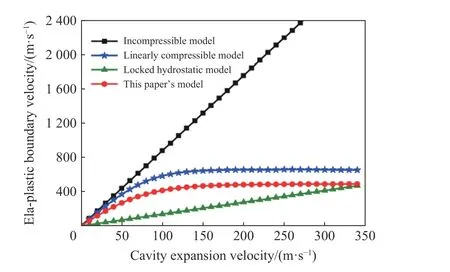
圖12 空腔速度與彈塑性界面移動速度的關(guān)系[38]Fig. 12 The relation between the velocity of the cavity and elastoplastic interface[38]
靶體材料對空腔膨脹模型的影響首先體現(xiàn)在響應(yīng)區(qū)的劃分上,材料的力學(xué)特性決定了其響應(yīng)區(qū)的復(fù)雜性;從簡單的塑性-彈性分區(qū)到復(fù)雜的塑性-密實-孔隙壓實-開裂-彈性分區(qū),不同響應(yīng)分區(qū)下計算結(jié)果有較大差異,正因為分區(qū)的復(fù)雜性,應(yīng)謹(jǐn)慎根據(jù)材料破壞特性準(zhǔn)確地劃分響應(yīng)分區(qū)。
2.2 屈服準(zhǔn)則及狀態(tài)方程
許多學(xué)者致力于采用更加準(zhǔn)確的塑性區(qū)屈服準(zhǔn)則描述空腔膨脹模型中塑性區(qū)的力學(xué)特性。常用的屈服準(zhǔn)則有:Mohr-Coulomb 屈服準(zhǔn)則、Griffith 屈服準(zhǔn)則、Drucker-Prager 蓋帽模型、Hoek-Brown 準(zhǔn)則、統(tǒng)一強度理論、應(yīng)變梯度塑性流動理論、Voce 應(yīng)變硬化準(zhǔn)則等。此外,材料的狀態(tài)方程從簡單的線性壓力-體積應(yīng)變逐漸向非線性多段式狀態(tài)方程演化,并考慮材料的可壓縮性、剪切飽和等。空腔膨脹模型之間主要區(qū)別在于對塑性區(qū)(粉碎區(qū))本構(gòu)的描述。總的來講,材料強度準(zhǔn)則、狀態(tài)方程的不斷修正以及考慮響應(yīng)過程中材料的可壓縮性,使得空腔膨脹模型能夠更加全面、準(zhǔn)確地描述材料的動態(tài)響應(yīng),但也使得需要求解的參數(shù)增加,方程無法得到解析解,計算過程越來越繁瑣。常見的屈服準(zhǔn)則與狀態(tài)方程如表1 所示。

表1 常見的幾種屈服準(zhǔn)則與狀態(tài)方程Table 1 Several common yield criteria and equations of state
應(yīng)變率、剪脹性、壓力-體積應(yīng)變等對空腔膨脹模型計算結(jié)果的影響主要體現(xiàn)在本構(gòu)方程上,進(jìn)而影響模型計算的空腔邊界速度、彈塑性邊界速度、空腔邊界應(yīng)力等。空腔膨脹模型的復(fù)雜性在于其本構(gòu)模型的選取,眾多的本構(gòu)方程使有關(guān)空腔膨脹模型方面的成果十分豐富。不同本構(gòu)方程代入求解后計算所得空腔邊界應(yīng)力差異較大,需要結(jié)合實際情況,合理分析、選取恰當(dāng)?shù)谋緲?gòu)方程描述材料的力學(xué)特性。
2.3 空腔膨脹模型的適用性
數(shù)十年來,柱形空腔膨脹(cylindrical cavity expansion,CCE)和球形空腔膨脹(spherical cavityexpansion,SCE)模型的研究都在Goodier[51]工作的基礎(chǔ)上進(jìn)行。CCE 和SCE 模型基于以下兩個基本假設(shè):
(1)施加在彈體表面上的接觸壓力p可以近似為在CCE 或SCE 模型中擴張空腔所需的壓力p0;
(2)空腔膨脹速度a˙ 可由彈體形狀以及當(dāng)前的軸向侵徹速度vz確定。
近年來,一些學(xué)者重新討論了該假設(shè)的適用性。Rubin[52]通過使用OR(ovoid of rankine)模型[24,53]作為基準(zhǔn),與空腔膨脹模型計算結(jié)果對比,分析空腔膨脹模型中由于不真實的流場導(dǎo)致的計算侵徹阻力誤差。OR 模型中的彈體頭部形狀及穩(wěn)態(tài)流場如圖13~14 所示,OR 模型用于分析剛性彈體侵徹不可壓縮的理想彈塑性材料的運動過程,其彈體形狀與穩(wěn)態(tài)真實流場一致。Rubin[52]認(rèn)為CCE 和SCE 模型均低估了靜態(tài)阻力值Rt,慣性項的存在彌補了部分侵徹阻力預(yù)測偏差值。總的來說,空腔膨脹模型對于較低的沖擊速度值會低估侵徹阻力,而對于較高的沖擊速度值會高估侵徹阻力,如圖15 所示。
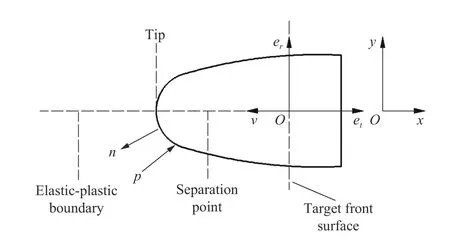
圖13 剛體侵徹不可壓縮理想彈塑性目標(biāo)的頭部區(qū)域示意圖[52]Fig. 13 Sketch of the nose region of a rigid projectile penetrating an incompressible elastic-perfectly plastic target[52]
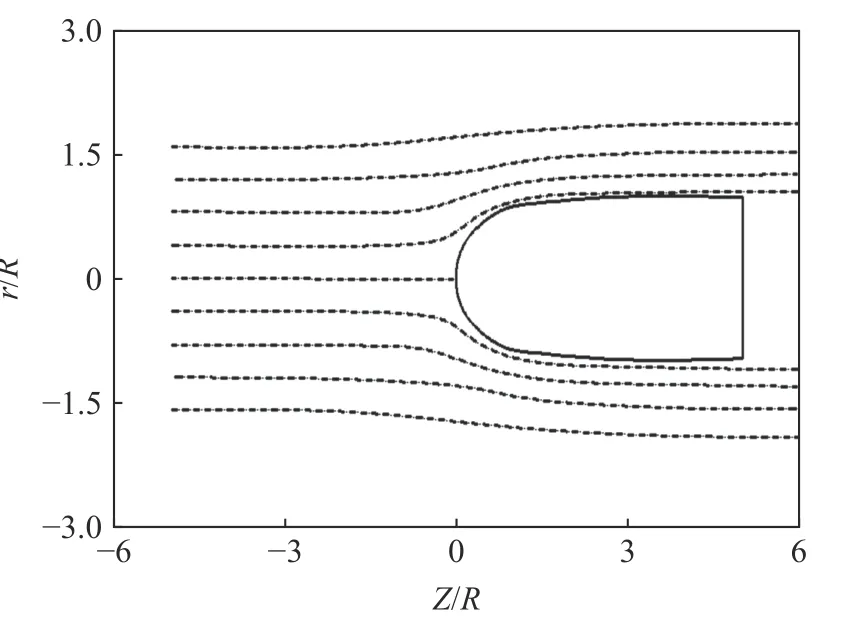
圖14 Rankine 形彈體的穩(wěn)態(tài)流場[53]Fig. 14 Steady-state flow field for an ovoid of Rankine shaped projectile[53]
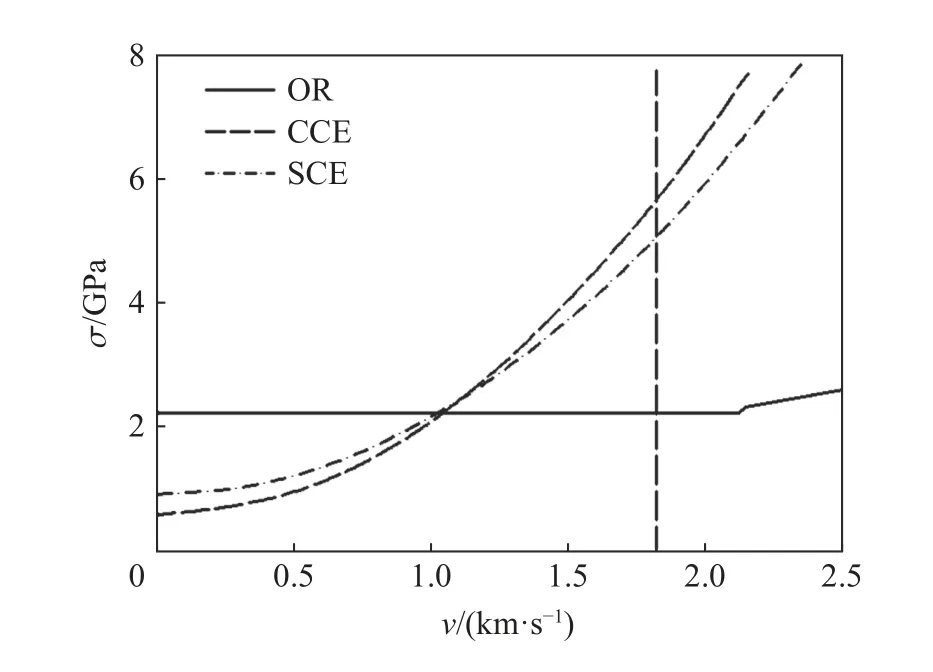
圖15 OR、CCE 和SCE 模型預(yù)測的侵徹速度平均軸向阻力應(yīng)力[52]Fig. 15 Average axial resistance stress as a function of the penetration velocity predicted by the OR, CCE and SCE models[52]
Rosenberg 等[22-23]、Kawata[54]、Kong 等[55]、Yankelevsky 等[25-26]、Feldgun 等[56]研究表明,在臨界速度范圍內(nèi)(空化速度),撞擊金屬目標(biāo)的剛性彈體上的侵徹阻力實際上是恒定的,而不是速度依賴性的,當(dāng)速度超過了臨界速度,則必須將慣性項加入到侵徹阻力中。恒定的侵徹阻力Rt取決于材料的特性(屈服強度和楊氏模量)以及彈頭的頭部形狀。即只要侵徹隧道區(qū)直徑與彈體直徑相同,可以認(rèn)為施加在彈體軸向方向的侵徹阻力是恒定的,侵徹深度可以由下式得出:
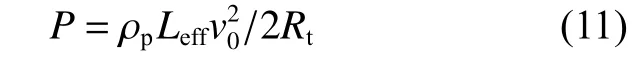
式中: ρp是彈體密度,Leff為彈體有效長度,v0為侵徹初始速度。
動態(tài)空腔膨脹模型普遍采用相似變換求解[57-59],理論求解一般不考慮材料的瞬態(tài)響應(yīng)行為,以獲得穩(wěn)定的自相似響應(yīng)。近年來,Rodríguez等[60]、Masri 等[61]研究了自相似穩(wěn)態(tài)場的時間尺度,利用數(shù)值模擬方法分析了空腔膨脹初始階段材料的瞬態(tài)響應(yīng)問題。圖16 為不同時間下空腔邊界應(yīng)力的數(shù)值模擬與理論計算值對比,從圖中可以看出,隨著時間的增加,數(shù)值模擬結(jié)果逐漸靠近理論解。Rodríguez 等[60]研究表明,相似變換所假設(shè)的自相似穩(wěn)態(tài)場存在,達(dá)到自相似穩(wěn)態(tài)場的時間在2.5~40 μs (與材料有關(guān))。因此當(dāng)采用空腔膨脹模型求解薄板侵徹問題時,由于自相似穩(wěn)態(tài)場的形成需要時間,應(yīng)慎重考慮采用空腔膨脹模型求解的合理性。
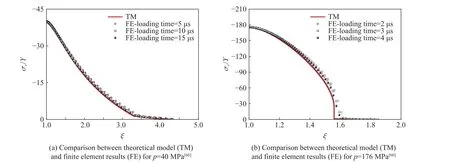
圖16 不同壓力時數(shù)值模擬與理論值對比[60]Fig. 16 Comparison between numerical simulation and theoretical values at different pressures[60]
侵徹模型(如Poncelet 模型、Recht-Ipson 模型、A-T 模型、空腔膨脹模型、Ravid-Bodner 模型和Walker-Anderson 模型等)各有其假設(shè)與適用條件[62]。盡管空腔膨脹模型存在著諸如無法預(yù)測空化現(xiàn)象、模型流場與實際有誤差等問題,但其仍然是侵徹問題研究中重要的分析手段。
3 靶體空腔膨脹阻力的數(shù)值模擬方法
空腔膨脹模型的中心思想是為了求得空腔表面徑向應(yīng)力與膨脹速度的關(guān)系,傳統(tǒng)的空腔膨脹理論研究方法均是基于理論分析和推導(dǎo),然后進(jìn)行大量的理論計算,但面對復(fù)雜的本構(gòu)條件、屈服準(zhǔn)則以及狀態(tài)方程時則遇到了瓶頸。利用數(shù)值模擬研究空腔膨脹過程是十分有效的, 數(shù)值模擬可以代替模型中某些復(fù)雜的理論推導(dǎo)部分, 根據(jù)模擬結(jié)果可以擬合得到空腔表面徑向應(yīng)力與膨脹速度的關(guān)系。
3.1 空腔表面恒定速度數(shù)值模擬
Warren 等[63]在研究混凝土的侵徹問題時采用了數(shù)值模擬的方法來確定球形空腔表面應(yīng)力,有限元模型與計算結(jié)果如圖17~18 所示。模擬假設(shè)空腔表面以恒定速度向外擴展,當(dāng)材料響應(yīng)趨于穩(wěn)定時,空腔表面的應(yīng)力也將趨于一個恒定值。通過改變空腔的膨脹速度,經(jīng)過一系列的模擬,可以得到徑向應(yīng)力與空腔膨脹速度的擬合關(guān)系式。
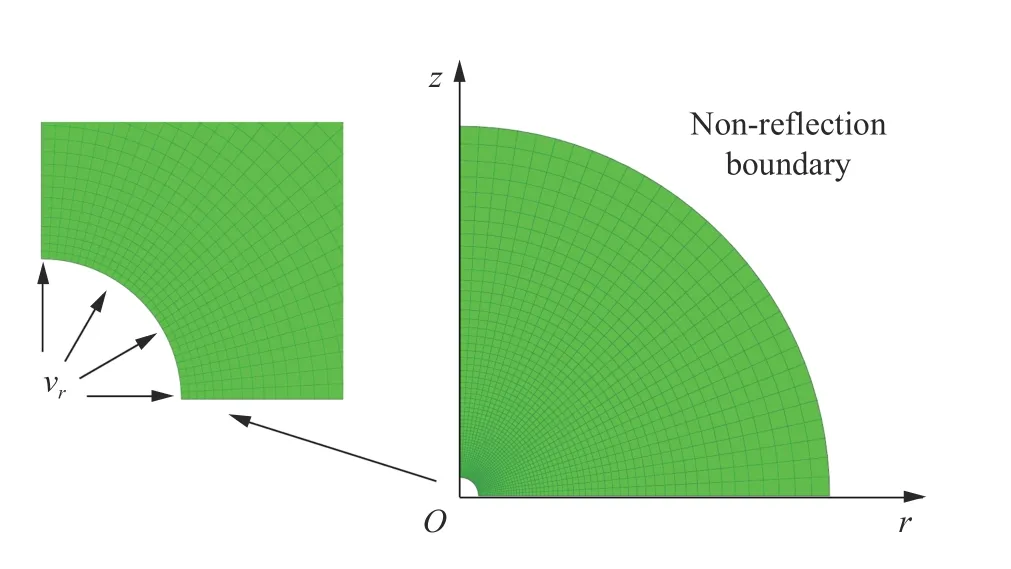
圖17 球形空腔膨脹計算的有限元模型Fig. 17 Finite element model for spherical cavity expansion calculation
何濤等[5]分別采用軸對稱單元和平面應(yīng)變單元來模擬典型靶體球形空腔膨脹和柱形空腔膨脹作用過程,如圖19~20。模型中靶板材料采用雙線性本構(gòu),模擬結(jié)果與可壓縮的理想彈塑性解接近,表明采用有限元數(shù)值模擬方法可以較為準(zhǔn)確地計算出空腔膨脹響應(yīng)力結(jié)果。
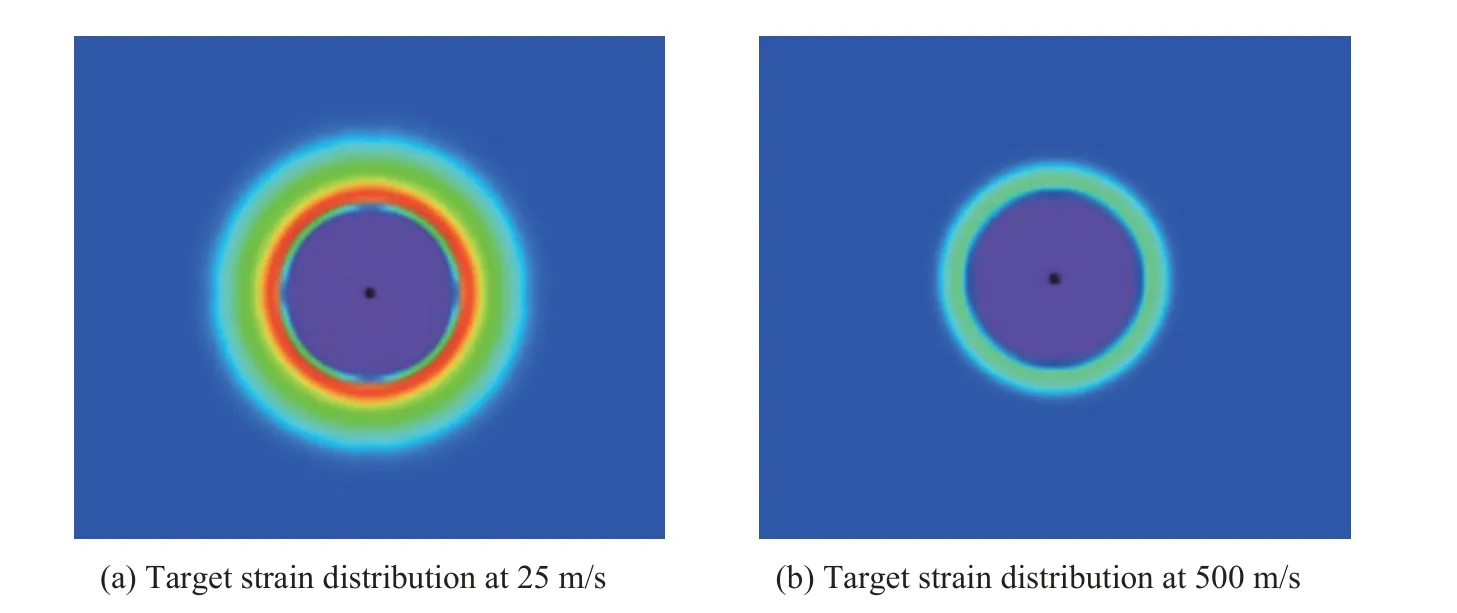
圖18 不同膨脹速度下靶體應(yīng)變分布[63]Fig. 18 Target strain distribution at different expansion velocities[63]
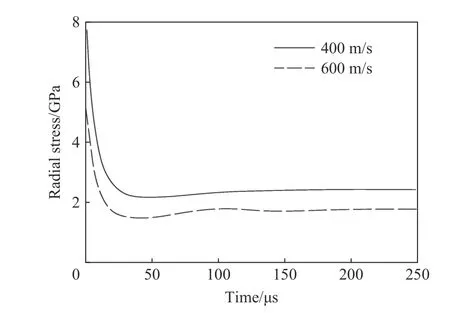
圖19 球形空腔分別以400 m/s 和600 m/s 的速度膨脹時得到的空腔表面徑向應(yīng)力隨時間變化曲線[5]Fig. 19 Radial stress at the spherical cavity surface versus time for cavity expansion velocities of 400 m/s and 600 m/s[5]
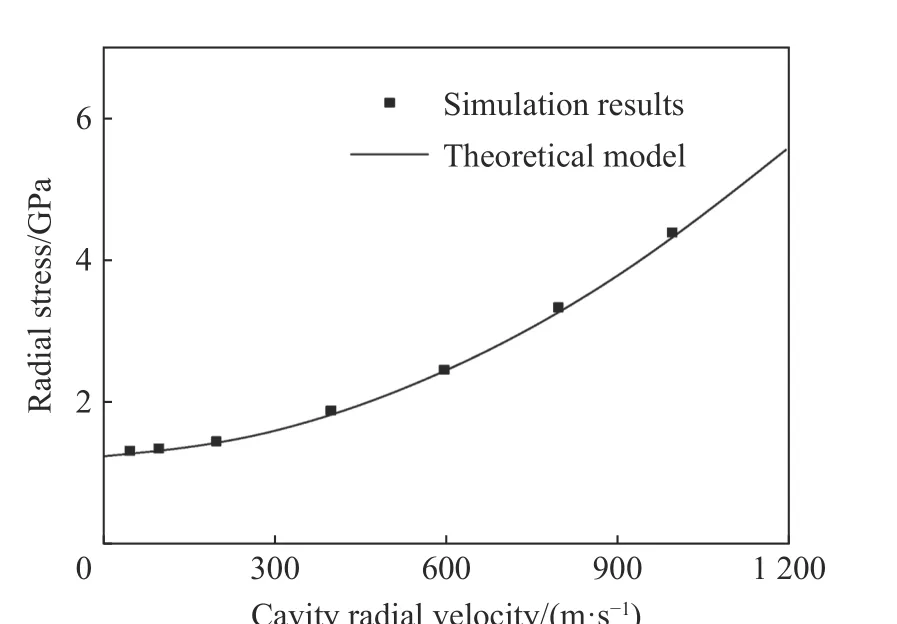
圖20 空腔表面徑向應(yīng)力隨空腔膨脹速度的變化曲線[5]Fig. 20 Radius stress at cavity surface versus cavity expansion velocity[5]
Rosenberg 等[59,64]對半無限理想彈塑性金屬材料進(jìn)行了一系列的研究,通過材料參數(shù)的單因素影響模擬研究,結(jié)合理論分析,得到了球形空腔徑向應(yīng)力系數(shù)與彈塑性材料基本參數(shù)的表達(dá)式。對于任意的彈塑性材料,均可由表達(dá)式計算出徑向應(yīng)力,誤差不超過5%,說明數(shù)值模擬可以直接反映出簡單本構(gòu)中各參數(shù)的聯(lián)系,增強了數(shù)值模擬的適用性。
圖21 是長桿彈以2 km/s 的速度撞擊材料和空腔以2 km/s 的速度壓縮材料時材料的速度分布圖。兩幅圖中的顏色代表材料的流動速度,且具有相同的標(biāo)尺,即顏色相同代表流動速度相同。從圖中可以看出,彈坑和空腔的形狀以及他們周圍的材料速度分布非常相似,證明了模擬方法的有效性。
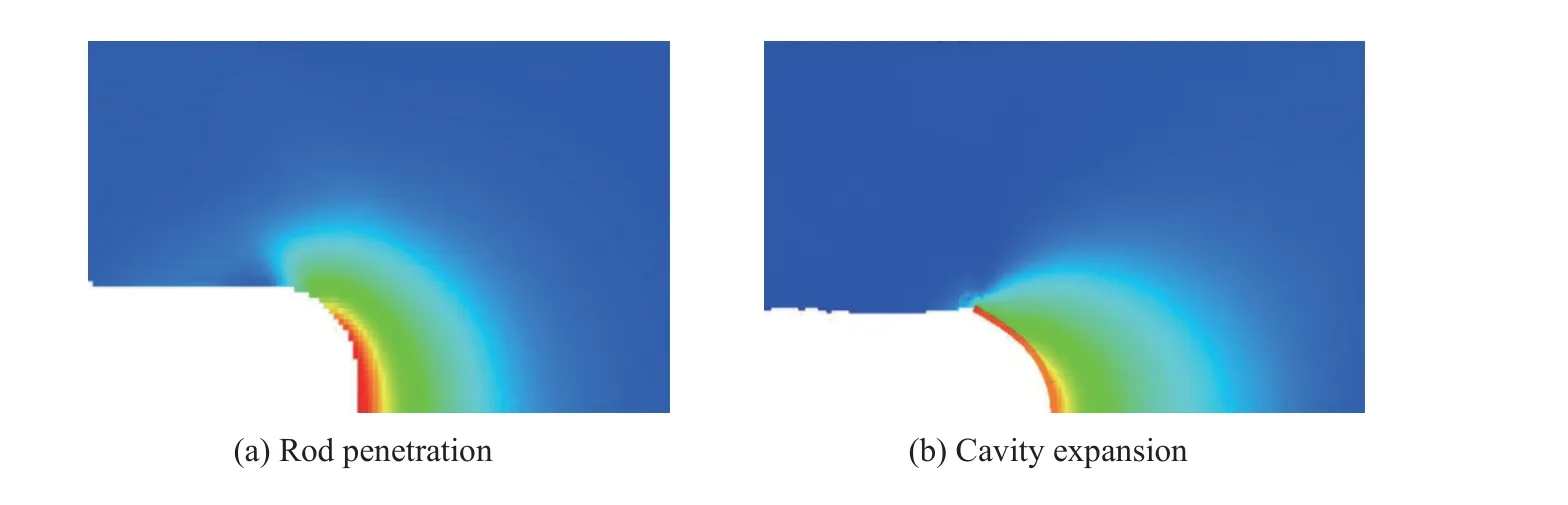
圖21 長桿彈侵徹坑附近和1/2 面積受內(nèi)壓的膨脹空腔附近的速度場[59]Fig. 21 Velocity field near long rod projectile penetrating crater and 1/2 area expansion cavity under internal pressure[59]
前人大部分工作集中在膨脹速度恒定的條件下得出各區(qū)域的大小,而實際情況中空腔膨脹速度是不斷變化的。牛振坤等[65]采用剛性彈侵徹混凝土,研究靶體材料各響應(yīng)區(qū)域的大小,并討論侵徹速度(空腔膨脹速度)對混凝土各響應(yīng)區(qū)域的影響。圖22~23 表明,隨著彈體侵徹速度的增高,混凝土粉碎區(qū)和破裂區(qū)邊界速度也隨之增高。
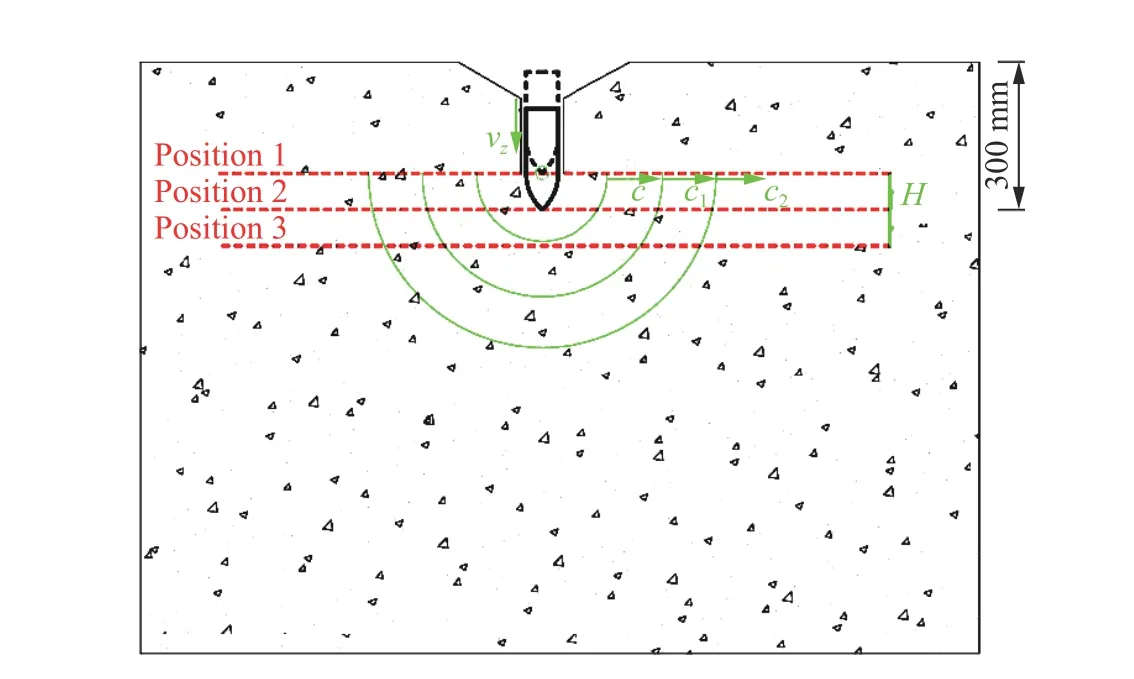
圖22 混凝土響應(yīng)分區(qū)形成過程[65]Fig. 22 Formation process of concrete target response regions[65]
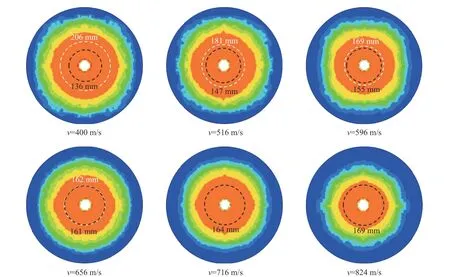
圖23 不同侵徹速度下的混凝土等效應(yīng)變云圖[65]Fig. 23 The equivalent strain diagrams of concrete under different penetration velocities[65]
3.2 空腔表面恒定壓力數(shù)值模擬
王一楠等[66]、晉小超等[67]等通過改變數(shù)值模擬中材料的失效判據(jù),對侵徹過程中金屬、混凝土靶空腔膨脹響應(yīng)區(qū)域進(jìn)行了識別劃分,得到了侵徹過程中混凝土各響應(yīng)區(qū)的區(qū)域大小。
圖24~25 為模型計算結(jié)果,該結(jié)果表明,在達(dá)到一定膨脹壓力后,空腔邊界將以對應(yīng)于膨脹壓力的恒定速度膨脹,證明存在理論所示的函數(shù)關(guān)系;進(jìn)一步分析表明,空腔邊界以恒定速度膨脹所需要的膨脹壓力閾值與混凝土的抗壓強度基本呈線性關(guān)系。
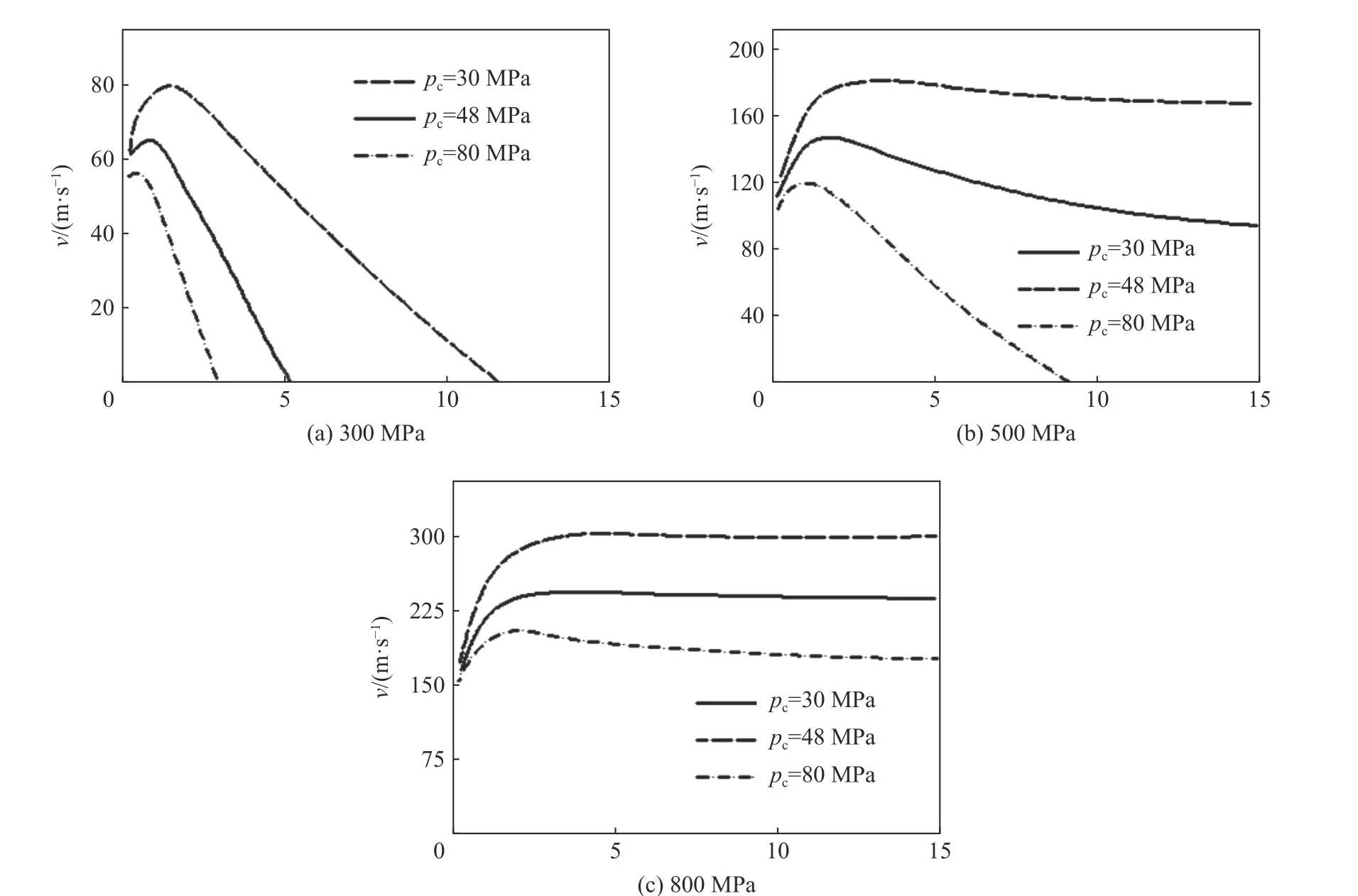
圖24 3 種強度混凝土在不同膨脹壓力下的空腔邊界速度時間歷程數(shù)值模擬結(jié)果[66]Fig. 24 Simulation results of cavity wall velocities for three strengths concrete with different expansion pressures[66]
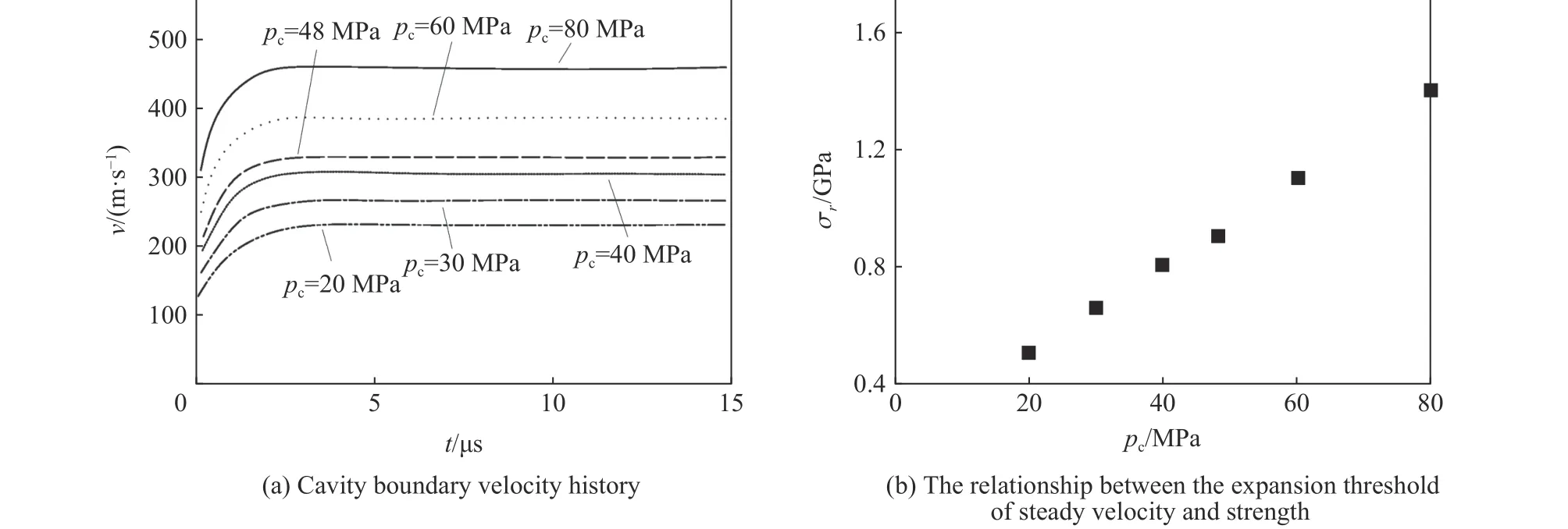
圖25 抗壓強度分別為20、30、40、48、60、80 MPa 混凝土的膨脹壓力閾值[66]Fig. 25 Threshold values of expansion pressures for concrete strength of 20, 30, 40, 48, 60, and 80 MPa[66]
采用數(shù)值模擬方法可以比較容易地確定出空腔膨脹時徑向應(yīng)力的大小,從而避免繁瑣的理論推導(dǎo)過程,同時充分考慮了材料在空腔膨脹過程中的實際響應(yīng)情況。另一方面,數(shù)值模擬手段可以應(yīng)用到各種復(fù)雜的本構(gòu)材料中,為解決具有復(fù)雜力學(xué)響應(yīng)特點的靶體材料的空腔膨脹作用過程提供了一個有效的模擬方法。
目前空腔膨脹的數(shù)值模擬工作集中在空腔表面單元法線方向施加恒定的速度以研究單元膨脹過程壓力,或在單元法線方向施加恒定壓力載荷以研究單元膨脹速度,主要針對理想侵徹條件的穩(wěn)定侵徹階段,即均勻擴孔速度對應(yīng)于恒定空腔膨脹壓力;尚未見到有限空腔膨脹的數(shù)值模擬,其原因是由于徑向的彈性位移受到限制,有限空腔膨脹的均勻擴孔速度不對應(yīng)于恒定空腔膨脹壓力[68]。
4 非理想侵徹條件的空腔膨脹壓力計算模型
空腔膨脹模型將彈靶理想化,一般假設(shè)為柱形、球形彈體侵徹均質(zhì)無限厚靶體。隨著戰(zhàn)斗部搭載平臺的演變、彈體結(jié)構(gòu)設(shè)計和防護工程等技術(shù)的不斷發(fā)展,彈靶條件變得復(fù)雜,經(jīng)典空腔膨脹模型適用性降低,需要針對經(jīng)典空腔膨脹模型進(jìn)行改進(jìn)。空腔膨脹阻力模型在多層復(fù)合靶板、間隔靶板、約束靶體、彈體刻槽和異形截面形狀彈體等彈靶條件下的應(yīng)用問題成為了一個重要的研究方向。
4.1 簡單多層復(fù)合靶體的空腔膨脹模型
一維半無限柱形/球形空腔膨脹模型中,空腔徑向壓力完全取決于材料自身的屬性,而實際應(yīng)用中會涉及到具有有限幾何尺寸的防護結(jié)構(gòu)。研究表明[69],有限邊界的存在會嚴(yán)重影響防護結(jié)構(gòu)的抗侵徹能力,將空腔膨脹模型推廣到復(fù)雜靶體結(jié)構(gòu),特別是多層復(fù)合靶體是侵徹力學(xué)研究者近期關(guān)注的熱點之一[70]。
Satapathy[71]分析了陶瓷材料鋪覆在半無限金屬材料上的抗侵徹阻力特性,假定橫向尺寸是無限的,可以忽略有限的橫向邊界的影響。針對不同的邊界條件,提出了如圖26 的4 種不同的響應(yīng)分區(qū)。
4 種響應(yīng)求解過程類似,在此列舉圖26(a)所示響應(yīng)區(qū)的求解過程,此時陶瓷材料具有4 個區(qū)域:空腔、粉碎、破裂和彈性,金屬基底是彈性的。不同區(qū)域的解可以通過空腔膨脹模型求得( σr即為空腔表面徑向應(yīng)力):

圖26 4 種可能的情況下的腔輪廓原理圖[71]Fig. 26 Schematic of cavity profiles for four-different possible scenarios, in ceramic targets backed by semi-infinite metal[71]
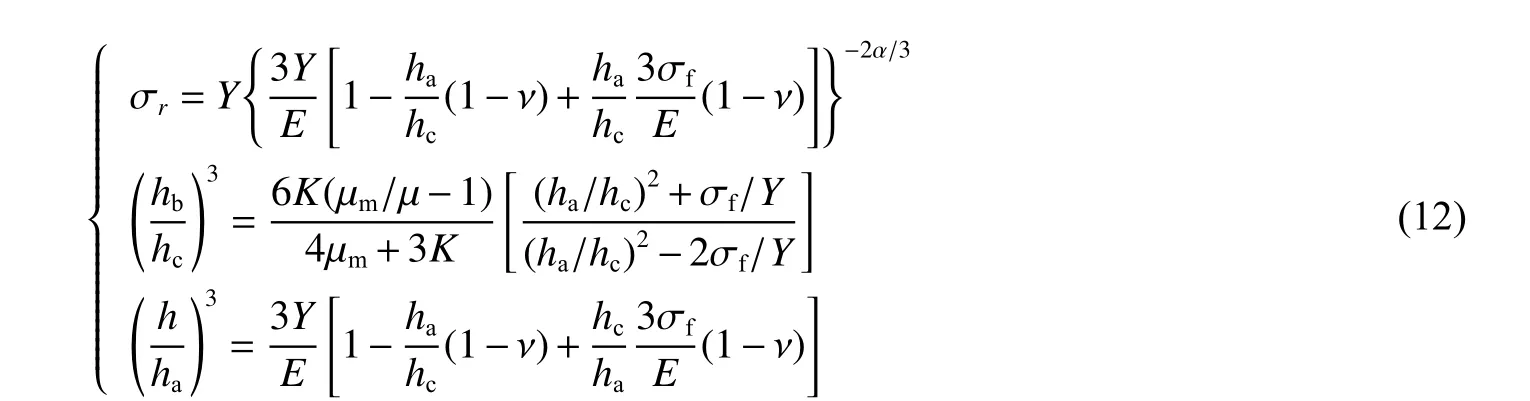
式中:ha、hb、hc、hd、h為分區(qū)常數(shù), σf為屈服極限, μ 為拉梅常數(shù), μm為金屬的剪切模量。
Satapathy[71]的研究表明,對于侵徹體尖端至邊界距離大于15 倍空腔直徑的情況,可以忽略有限邊界的影響;當(dāng)該比值小于10 時,必須考慮邊界效應(yīng)。
4.2 給定載荷下任意截面輪廓空腔邊界應(yīng)力分析
在一維空腔膨脹理論方面已有大量的研究成果,但在任意截面輪廓空腔膨脹理論的研究方面卻鮮有報道。任意截面輪廓空腔膨脹理論面臨的主要問題是確定將塑性區(qū)與彈性區(qū)域分開的輪廓(彈塑性邊界),以使應(yīng)力和位移在整個邊界兩側(cè)都是連續(xù)的函數(shù),一旦彈塑性邊界確定,模型就可以簡化為純彈性區(qū)與純塑性區(qū)。
Woo[72]依據(jù)彈塑性動力學(xué)理論推導(dǎo)了任意截面形狀的柱形空腔膨脹模型,靶體材料分為空腔區(qū)、彈性區(qū)和塑性區(qū)。通過應(yīng)力狀態(tài)判斷靶體介質(zhì)的屈服狀態(tài)及介質(zhì)所處的空腔膨脹模型分區(qū)位置。利用最小二乘法擬合與迭代法最終可得到橢圓形空腔膨脹過程中邊界徑向應(yīng)力與速度的關(guān)系:

式中:A1的值取為1.422,K和 ρt分別為靶體材料體積模量和密度,A2是與橢圓截面彈體橫截面尺寸有關(guān)的參數(shù)。
任意截面輪廓空腔膨脹模型與傳統(tǒng)空腔膨脹模型所求得的彈靶接觸面阻力函數(shù)形式類似,都表示為靜阻力項和慣性項之和,且慣性項都表示為速度的二次方函數(shù)。但不同的是,傳統(tǒng)空腔模型中靜阻力項與材料的無圍抗壓強度有關(guān),而任意截面輪廓空腔模型中靜阻力項與材料的體積模量相關(guān)。
Woo[72]結(jié)合阻力函數(shù)建立了侵徹動力學(xué)模型,進(jìn)一步分析了橢圓長短軸比對侵徹阻力、深度的影響規(guī)律,計算結(jié)果如圖27 所示。研究表明,侵徹阻力與長短軸比呈正相關(guān),長短軸比越大,侵徹阻力越大、侵徹深度越小。
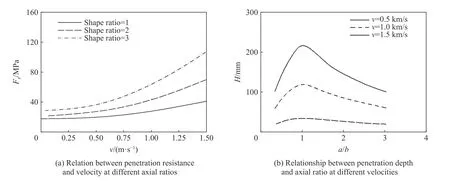
圖27 橢圓長短軸比對侵徹阻力、深度的影響規(guī)律[72]Fig. 27 Influence of ellipse axial ratio on penetration resistance and depth[72]
4.3 橢圓空腔膨脹過程中空腔邊界應(yīng)力分析
隨著彈靶侵徹問題研究的不斷深入,優(yōu)化后的彈體形狀并不都是傳統(tǒng)的圓截面,侵徹過程中靶內(nèi)所形成的空腔也并不都是傳統(tǒng)的球形和柱形。
為了描述橢圓截面彈體侵徹過程中橢圓孔洞的擴張過程,王文杰等[73]采用靜態(tài)柱形空腔膨脹理論,通過假設(shè)靶體材料為理想線彈性材料,計算了橢圓孔口周圍的受力狀態(tài),模型示意圖如圖28 所示。
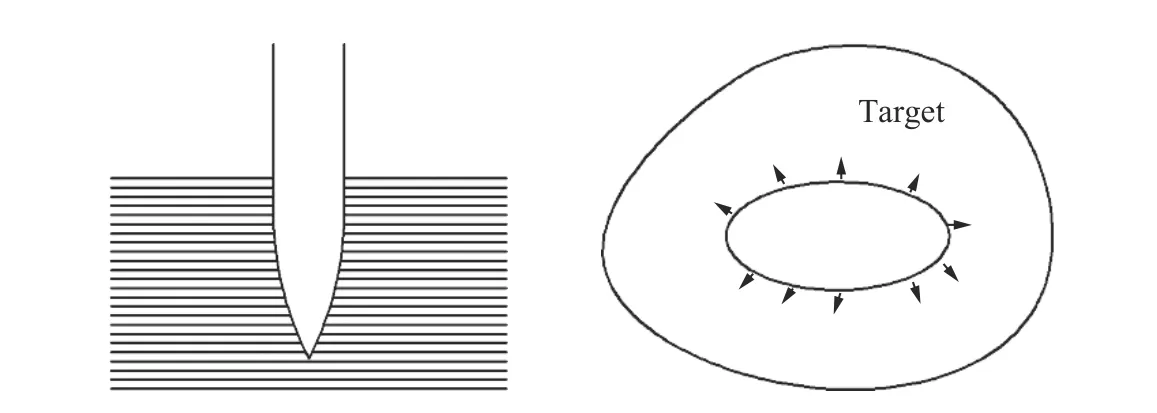
圖28 橢圓孔受力狀態(tài)示意圖[73]Fig. 28 Diagram of stress state of elliptical hole[73]
忽略分布在物體體積內(nèi)的力,例如重力和慣性力等,彈性力學(xué)平面問題歸結(jié)于求解雙調(diào)和方程:

通過引入復(fù)變數(shù),利用保角變換,加上應(yīng)力邊界條件,最終求得復(fù)勢函數(shù)φ(ξ)和ψ(ξ)。將求得的φ(ξ)和ψ(ξ)代入應(yīng)力函數(shù)便可求得橢圓空腔擴張過程中孔周應(yīng)力分布情況:
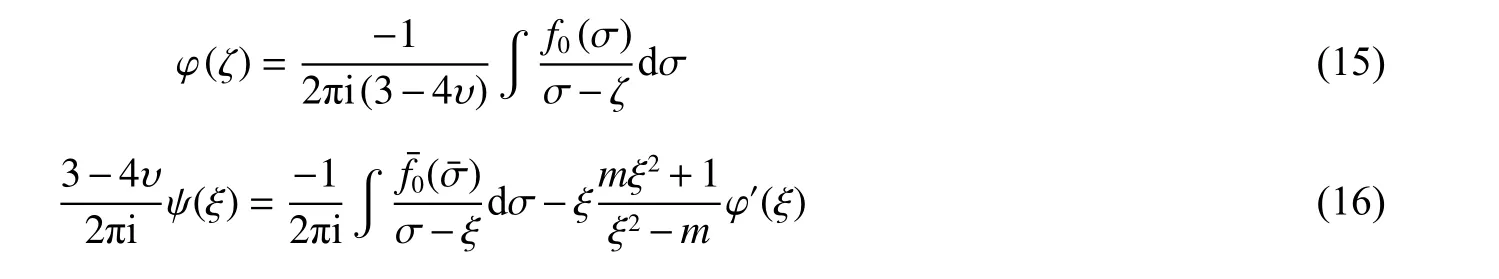
當(dāng)橢圓空腔受均勻壓力向外擴張時,圖29為計算所得橢圓空腔內(nèi)壁在 0 ~π/2 上的受力曲線。由圖29可知,橢圓空腔內(nèi)壁受均勻壓力向外膨脹時,空腔長軸端點處受力最大,而在短軸端點處受力最小。
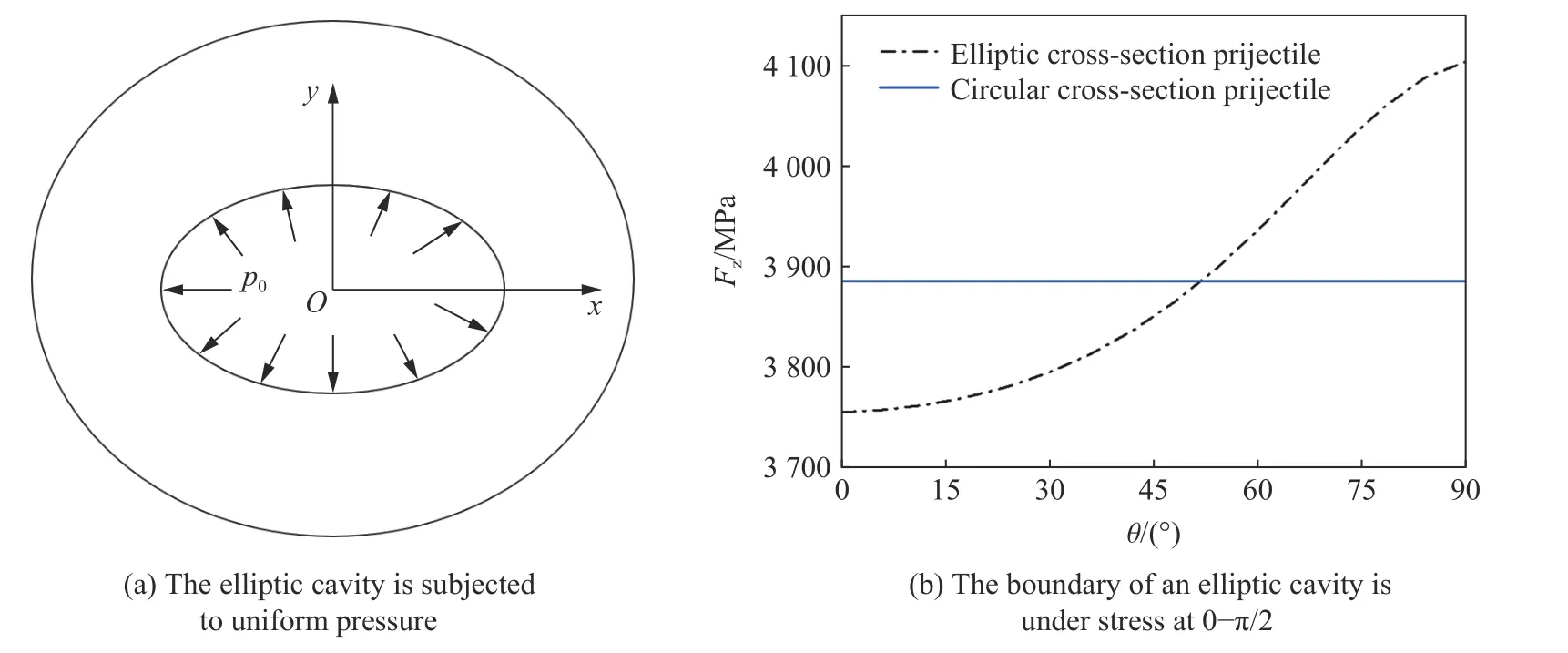
圖29 橢圓空腔邊界受力狀態(tài)[73]Fig. 29 The state of force at the boundary of an elliptic cavity[73]
4.4 考慮軸向壓縮-切向剪切聯(lián)合作用下的空腔膨脹模型
基于混凝土材料抗壓不抗剪的特點,鄧佳杰等[4]提出一種通過頭部刻槽實現(xiàn)非對稱結(jié)構(gòu)形式的彈體。該類型彈體在侵徹過程中可改變傳統(tǒng)結(jié)構(gòu)彈體侵徹單一壓縮破壞混凝土的模式,實現(xiàn)較優(yōu)的彈體侵徹毀傷能力。
假設(shè)在頭部非對稱刻槽彈體侵徹作用下,混凝土材料中出現(xiàn)柱形空腔,空腔分區(qū)示意圖如圖30 所示。此時,柱形空腔面以速度vc及旋轉(zhuǎn)角速度 ω 由初始零半徑向外徑向膨脹,混凝土材料在受徑向應(yīng)力的同時在各響應(yīng)區(qū)間產(chǎn)生周向旋轉(zhuǎn)作用,材料受力表現(xiàn)為軸向壓縮及切向剪切聯(lián)合作用力,此時柱坐標(biāo)下的空腔膨脹過程為二維受力狀態(tài)。
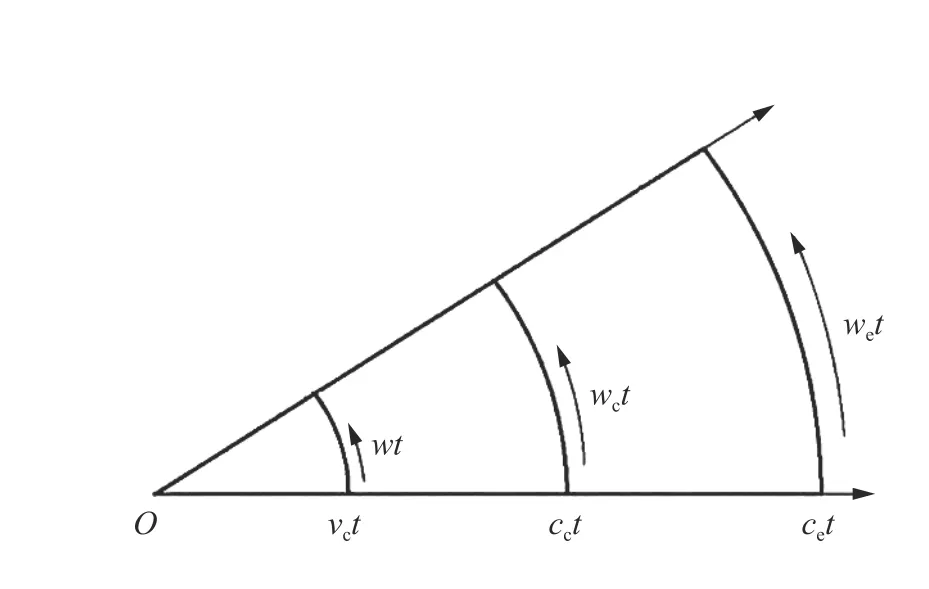
圖30 壓剪聯(lián)合作用下的空腔分區(qū)[4]Fig. 30 Cavity partition under combined action of compression and shear[4]
假設(shè)切向位移uθ與徑向位移ur滿足線性比例關(guān)系,uθ=kur,且旋轉(zhuǎn)角速度 ω 與徑向速度vc同時滿足ω=kvc。在考慮切向位移的情況下,屈服面半徑為Cs,常數(shù)C1、C2的表達(dá)式為:
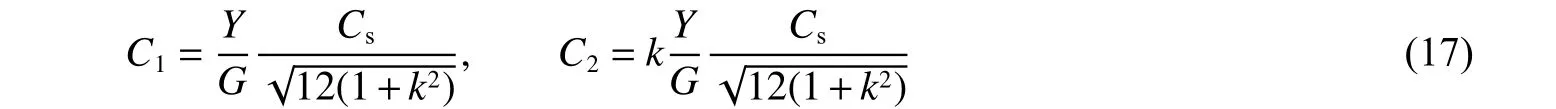
結(jié)合塑性區(qū)的屈服條件,得到考慮剪切效應(yīng)的靶體空腔膨脹徑向應(yīng)力隨空腔膨脹過程中空腔半徑間的關(guān)系式:
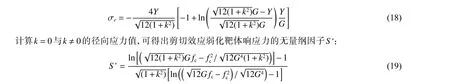
式中:fc為材料的抗壓強度。
如圖31 所示,考慮剪切效應(yīng)的二維空腔膨脹理論及局部相互作用模型的理論計算結(jié)果與實驗結(jié)果吻合較好。
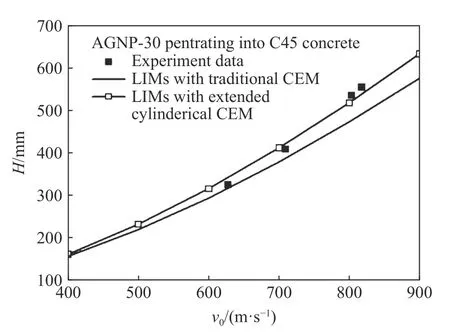
圖31 彈體侵徹深度理論與實驗對比[4]Fig. 31 Comparison of predicted and experimental DOP data[4]
4.5 有限/約束靶體的空腔膨脹理論
對于斜侵徹和有限尺寸金屬靶侵徹問題,自由邊界的影響不可忽略。Littlefield 等[74]運用實驗、近似解析解和數(shù)值模擬相結(jié)合的方法對有限直徑金屬厚靶側(cè)面自由邊界的影響進(jìn)行了探討,結(jié)果表明:自由邊界和靶體直徑對侵徹模式和侵徹深度有顯著影響,當(dāng)靶體與彈體直徑的比值小于20 時,靶體的侵徹阻力急劇降低。
Zhen 等[75-76]考慮材料可壓縮性和自由邊界徑向位移,改進(jìn)了現(xiàn)有不可壓縮理想彈塑性材料有限空腔膨脹理論,得到了更精確的空腔邊界壓力理論解。圖32 為彈塑性階段空腔壓力與空腔膨脹速度的關(guān)系。其中,r0=∞和rp/r0=1 分別代表無線球形空腔膨脹和有限球形空腔膨脹的彈塑性階段。結(jié)果表明,無限球形空腔膨脹模型比球形空腔膨脹模型的空腔壓力高9.3%~17.2%。圖33 為有限球形空腔膨脹模型塑性階段半徑大小對空腔壓力的影響,rc為給定空腔半徑,r0為球體半徑。結(jié)果表明,隨著rc/r0的增加,空腔壓力減小;rc/r0=0.5 情況下的空腔壓力比rc/r0=0.3 時低39.6%~37.5%,對于給定的空腔半徑rc,球體的初始半徑越小,空腔壓力越小。
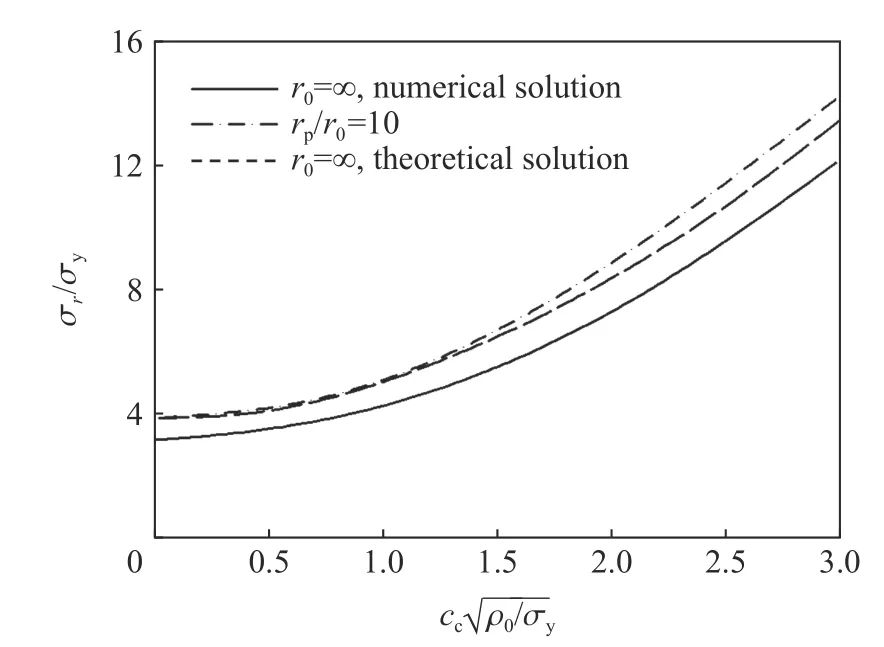
圖32 球形空腔壓力-空腔膨脹速度[76]Fig. 32 Spherical cavity pressure-cavity expansion velocity diagram[76]
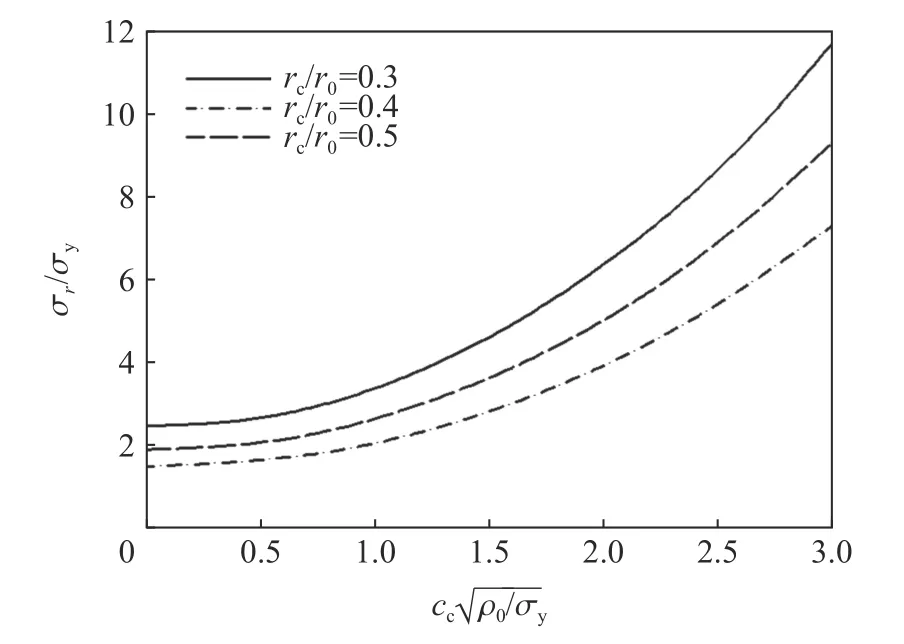
圖33 有限球形空腔壓力-空腔膨脹速度[75-76]Fig. 33 Pressure-cavity expansion velocity diagram of a finite spherical cavity[75-76]
混凝土三向受壓狀態(tài)下的極限強度和極限應(yīng)變比單軸抗壓高很多。采用結(jié)構(gòu)措施改善應(yīng)力狀態(tài)是提高普通混凝土抗侵徹性能的重要方法,對混凝土施加約束是提高混凝土抗侵徹性能的新途徑[68,77-79]。
曹揚悅也[80]基于粉碎區(qū)的Hoek-Brown 準(zhǔn)則,建立了約束混凝土準(zhǔn)靜態(tài)柱形和球形空腔膨脹模型,得到了各響應(yīng)模式的空腔邊界壓力及模式轉(zhuǎn)化條件。研究表明,約束混凝土的準(zhǔn)靜態(tài)擴孔過程可分為4 個階段,即無限介質(zhì)空腔膨脹階段、彈性-裂紋-粉碎響應(yīng)階段、裂紋-粉碎響應(yīng)階段和完全粉碎階段。各階段粉碎區(qū)混凝土均處于三向受壓狀態(tài),擴孔壓力隨空腔半徑增大而增大,進(jìn)入完全粉碎階段后增長迅速,且柱腔模型增幅更顯著。圖34 為柱形/球形空腔膨脹模型下約束強度對空腔邊界壓力的影響規(guī)律。
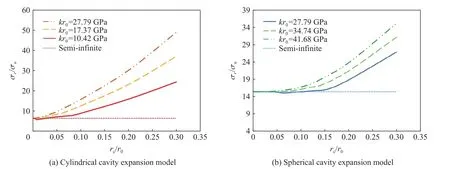
圖34 柱形/球形空腔膨脹模型下約束強度對空腔邊界壓力的影響規(guī)律[80]Fig. 34 Effect of confinement strength on boundary pressure of cylindrical/spherical cavity expansion model[80]
Meng 等[68]研究了鋼管約束的混凝土(STC)目標(biāo),基于改進(jìn)的Griffith 強度準(zhǔn)則,提出了具有徑向彈性限制的約束空腔膨脹模型,計算結(jié)果如圖35 所示。研究結(jié)果表明,約束混凝土中的空腔膨脹模型與半無限材料中的空腔膨脹模型不同,由于徑向的彈性位移受到限制,因此在給定膨脹速度下其空腔邊界應(yīng)力值不是恒定的。
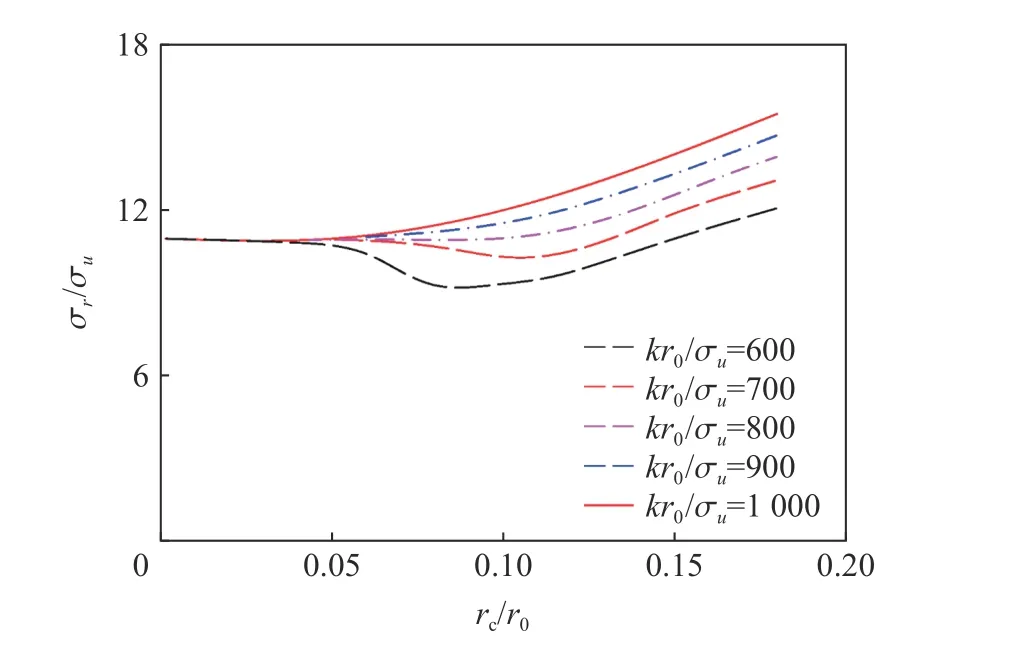
圖35 不同約束程度下徑向應(yīng)力與空腔速度的關(guān)系[68]Fig. 35 The transmutation discipline of radial stress at cavity wall[68]
綜上所述,通過合理簡化問題,針對任意空腔截面、壓剪耦合、有限/約束邊界等復(fù)雜彈靶條件,通過空腔膨脹模型可以得出問題的近似解。但模型不能反映侵徹問題的全部物理過程,也只適用于解決一定范圍內(nèi)的侵徹問題,且求解過程繁瑣,因此在適用性和可靠性方面受到限制。
5 空腔膨脹阻力模型在典型侵徹問題中的應(yīng)用
有關(guān)空腔膨脹模型的應(yīng)用,一方面是通過求解空腔膨脹模型,給出彈體侵徹阻力的解析表達(dá)式,然后根據(jù)運動學(xué)原理建立彈體運動方程,根據(jù)邊界條件和初始條件求解運動方程,得出侵徹過程中力、速度、位移隨時間變化的函數(shù);另一方面利用空腔膨脹模型結(jié)果替代彈頭受到的法向壓力,并與有限元法相結(jié)合進(jìn)行數(shù)值模擬,可以大幅減少有限元法的計算時間。
5.1 基于空腔膨脹模型阻力函數(shù)的高速侵徹流體動力學(xué)模型
在高速侵徹過程中,由于彈、靶界面的壓力遠(yuǎn)大于其材料的屈服強度,彈體頭部進(jìn)入流體侵徹狀態(tài),其侵徹過程可以用流體動力學(xué)方法近似描述。Tate[81-82]提出考慮彈、靶強度的修正伯努利方程來描述侵蝕彈體侵徹過程,其彈、靶界面平衡方程為:

式中:v為彈體尾部速度,u為彈體侵徹速度,Yp為彈體強度表征項,Rt為靶體強度表征項,ρp為彈體密度,ρt為靶體密度。
Rt值接近于靶體內(nèi)空腔擴展速度穩(wěn)定時的空腔邊界上的徑向應(yīng)力值,即Rt=-σr,部分學(xué)者基于空腔膨脹模型給出了Rt值的確定方法。圖36為流體侵徹示意圖。
圖36 流體侵徹示意圖Fig. 36 Schematic diagram of fluid penetration
Forrestal 等[83]確定了從零初始半徑打開球形空腔所需的準(zhǔn)靜態(tài)壓力,在Forrestal 的基礎(chǔ)上,Anderson 等[84]根據(jù)無限介質(zhì)中圓柱空腔膨脹的方法給出了Rt的計算方法; Godwin 等[85]基于任意假定的二維流動模式的分析模型定性地給出了Rt的值;Galanov 等[86-87]采用動態(tài)強度代替Satapathy[71]提出的模型中的靜態(tài)強度,給出了脆性材料的兩段式Rt計算公式;Lan 等[88]對界面粒子速度和壓力分布以及目標(biāo)中的響應(yīng)區(qū)域進(jìn)行了假設(shè),給出的Rt取決于彈體侵徹速度以及目標(biāo)材料在高溫下的力學(xué)性能。Rubin 等[89]通過空腔膨脹理論研究靶板中彈塑性邊界位置的極限值,并引入一個經(jīng)驗常數(shù)來表征這些極限值之間的過渡,給出了Rt的顯示表達(dá)式;表2 列舉了幾種典型的Rt表達(dá)式。

表2 不同 Rt 的表達(dá)式Table 2 Different values of Rt
5.2 高速動能彈體侵徹動力學(xué)模型
針對剛體侵徹問題已開展了較多的研究工作[65-66,91-100],已獲得了較為豐富的理論成果。其主要思想是結(jié)合已知的靶體阻力,將彈體頭部表面離散化,計算每個微元上的受力,通過曲面積分的方法,最終獲得彈體軸向方向的阻力,聯(lián)立彈體運動方程建立侵徹理論模型。

圖37 彈體結(jié)構(gòu)示意圖Fig. 37 Schematic diagram of missile body structure
通過空腔膨脹求解的徑向應(yīng)力等效為彈體頭部受力,彈體軸向受力可以簡化為如下所示的與速度相關(guān)的函數(shù):

式中: αs為 靶板阻力中靜阻力項, βs為慣性項。

表3 中列舉了其他幾種常見的采用空腔膨脹模型推導(dǎo)的侵徹深度P的預(yù)測公式。
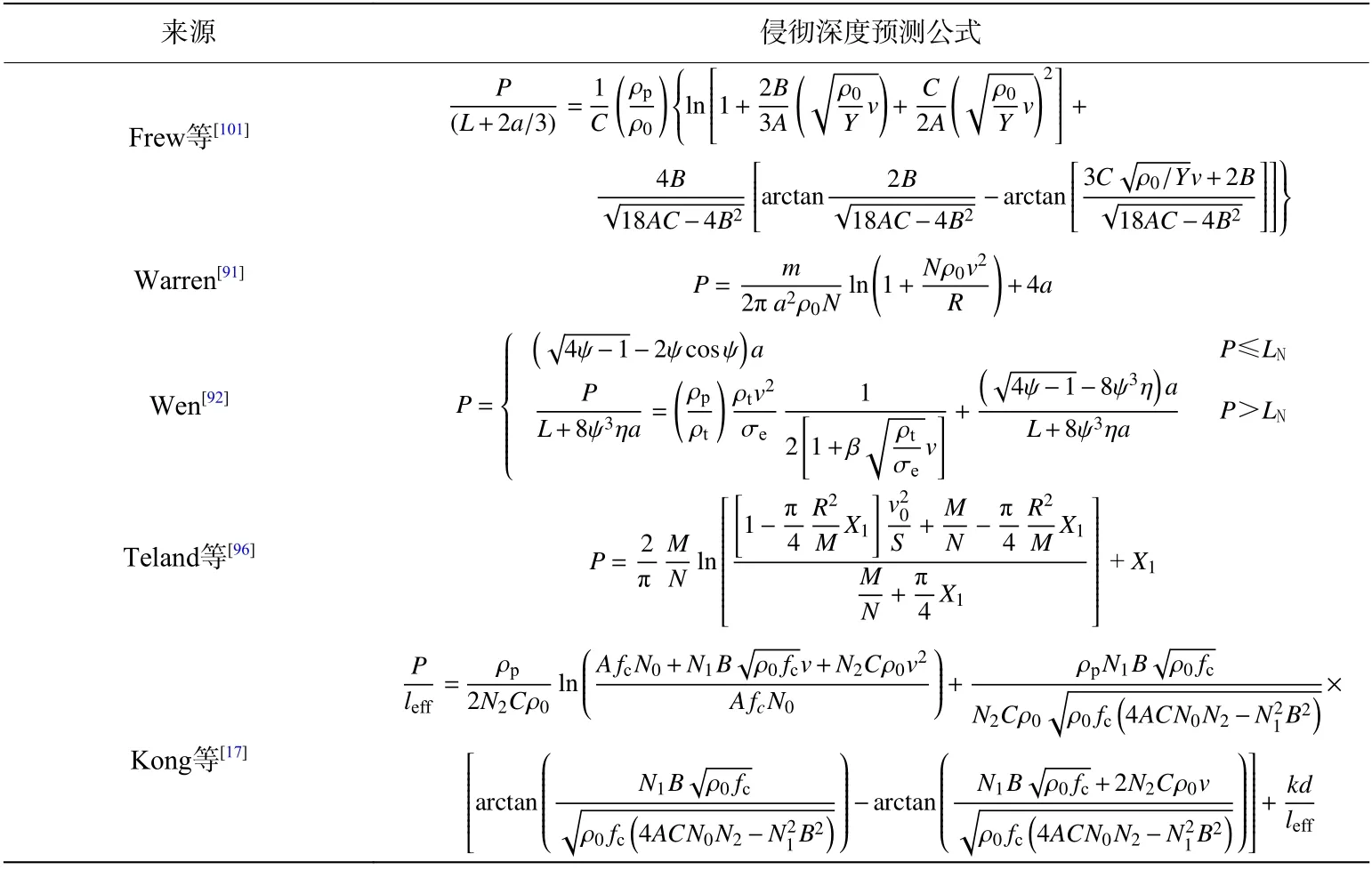
表3 侵徹深度理論預(yù)測公式Table 3 Theory prediction formula of penetration depth
5.3 基于空腔膨脹模型阻力函數(shù)的彈靶分離法
彈靶分離方法的基本思想是將侵徹過程中靶體的響應(yīng)簡化為與瞬時速度相關(guān)的函數(shù),即靶體響應(yīng)力函數(shù)。在數(shù)值模擬過程中,用靶體響應(yīng)力函數(shù)代替靶體對彈體的作用,從而省略靶體網(wǎng)格劃分及其變形過程中產(chǎn)生的網(wǎng)格畸變,同時無需考慮復(fù)雜的彈靶接觸問題,從而縮短運算時間[90-91],其作用原理圖如圖38 所示。
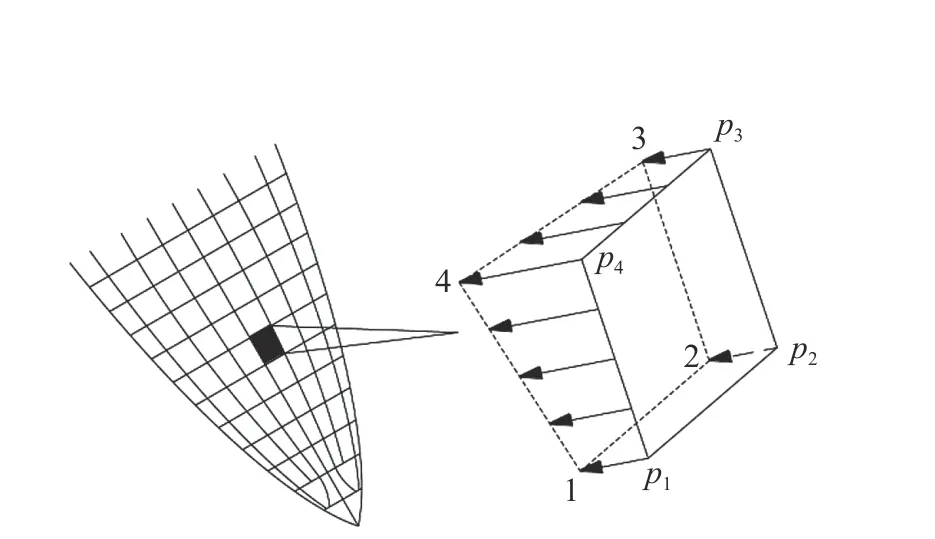
圖38 彈體表面單元受力定義Fig. 38 Definition of force on surface element of projectile body
Warren[91]將基于動態(tài)球形空腔膨脹理論得到的阻力函數(shù)嵌入到有限元程序PRONTO3D中,并且加入自由面效應(yīng)函數(shù)進(jìn)行修正,模擬彈體斜侵徹靶體,其計算結(jié)果如圖39 所示。研究表明,通過計算得到彈體侵徹過程中的變形和實驗結(jié)果較為符合,驗證了彈靶分離方法的可靠性。
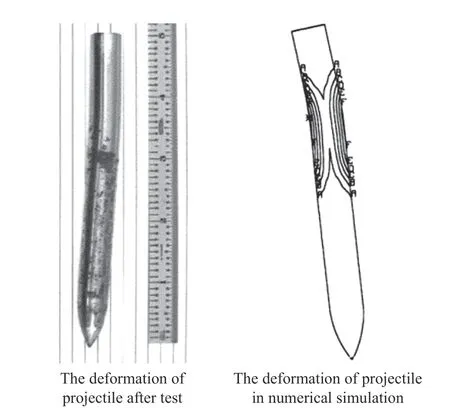
圖39 尖卵形彈體以459 m/s 的速度侵徹石灰石的實驗結(jié)果與數(shù)值模擬結(jié)果對比[91]Fig. 39 Comparison between the experimental and numerical simulation results of projectile penetrating limestone at the speed of 459 m/s[91]
何濤等[5]基于Warren 的處理方法系統(tǒng)地給出了預(yù)測動能彈侵徹和貫穿不同靶板的方法。王松川[102]基于彈靶分離的思想,考慮自由面效應(yīng)和彈靶分離再接觸效應(yīng)的影響,采用Fortran 語言編寫斜侵徹彈道計算程序,對剛性彈斜侵徹半無限石灰石靶和6061-T6511 鋁靶等問題進(jìn)行了計算研究,圖40 為彈體以45°入射角侵徹鋁靶實驗與仿真結(jié)果對比圖。研究結(jié)果表明,采用靶體響應(yīng)力函數(shù)的方法只適用于彈體以小碰撞角侵徹的情況,彈體速度較低時的計算結(jié)果與實際情況相差很大。
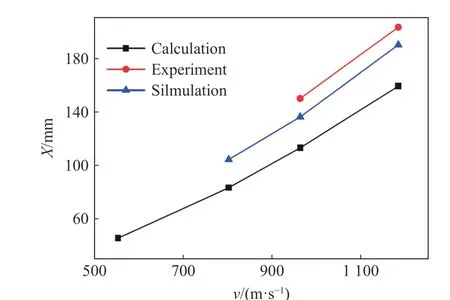
圖40 彈體以45°碰撞角斜侵徹金屬鋁靶的仿真與試驗結(jié)果對比圖[102]Fig. 40 Comparison of simulation and test results of oblique penetration of projectile into metal aluminum target at 45° impact angle[102]
康海峰等[103]基于彈靶分離的思想,根據(jù)空腔膨脹理論計算彈體侵徹阻力,考慮自由面效應(yīng),進(jìn)而對彈體進(jìn)行受力分析,再根據(jù)剛體運動學(xué)理論,推導(dǎo)彈體侵徹運動微分方程,建立動能侵徹彈非正侵徹混凝土介質(zhì)的動力學(xué)分析模型,可以快速計算彈體侵徹軌跡。閃雨等[104]基于空腔膨脹理論、改進(jìn)的自由面效應(yīng)模型及彈靶分離再接觸效應(yīng)建立了剛性/侵蝕彈體非正侵徹貫穿混凝土彈道軌跡預(yù)測方法,研究了彈靶結(jié)構(gòu)參數(shù)及彈體著靶姿態(tài)對侵徹彈道的影響規(guī)律,計算結(jié)果如圖41 所示。研究表明,計算非正侵徹彈道時,需考慮自由面效應(yīng)及彈靶分離再接觸效應(yīng);對于混凝土靶,采用改進(jìn)的自由面模型可有效預(yù)估彈體的侵徹彈道。
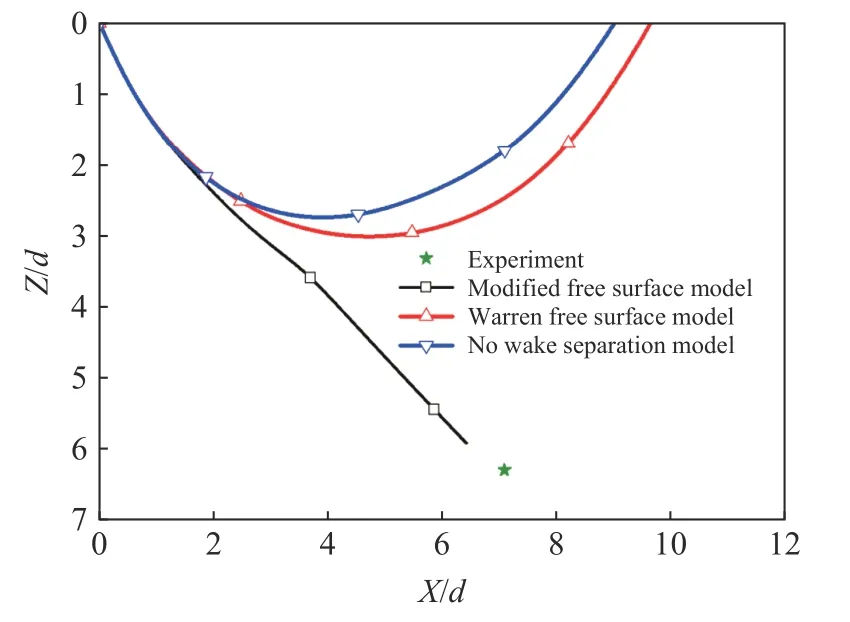
圖41 自由面模型、彈靶分離模型對侵徹彈道的影響[104]Fig. 41 Influence of free surface model and projectile separation model on penetration trajectory[104]
綜上所述,在高速/超高速侵徹方面,通過與空腔膨脹理論相結(jié)合,A-T 模型及改進(jìn)的A-T 模型發(fā)展迅速,但仍然存在諸如采用靜態(tài)空腔膨脹得到的常數(shù)Rt與實驗數(shù)據(jù)反向擬合和數(shù)值模擬計算所得結(jié)論相悖,大部分改進(jìn)模型或不具備預(yù)測能力或存在大量經(jīng)驗性參數(shù)或太過復(fù)雜不便工程應(yīng)用等缺點;在剛性侵徹方面,利用靶體響應(yīng)力函數(shù),可以通過侵徹動力學(xué)模型或彈靶分離的方法,快速獲得彈體終點參數(shù),但計算精度取決于靶體響應(yīng)力函數(shù),且在較高速度下,計算誤差逐漸增大。
6 總結(jié)與展望
近年來,空腔膨脹理論研究一方面集中在對材料本構(gòu)方程、初始邊界條件的修正,在側(cè)向約束、有限邊界、含鋼筋或骨料混凝土等方面取得較大進(jìn)展;另一方面,研究者們通過數(shù)值模擬的方法避開繁瑣的理論求解,加深了對模型中各參數(shù)間的理解。空腔膨脹模型作為侵徹問題理論分析的主要基礎(chǔ)理論之一,其考慮因素全面、適用情況廣泛、便于工程應(yīng)用等特點,為厘清高速侵徹問題提供了有力支撐。通過對相關(guān)文獻(xiàn)查閱、整理與分析,得到的主要結(jié)論與建議如下。
(1)空腔膨脹理論準(zhǔn)確性依賴于模型假設(shè)與材料特性,但真實、全面反映材料的屈服準(zhǔn)則與狀態(tài)方程復(fù)雜度增加了模型的求解難度。目前的研究對材料特性進(jìn)行了大量簡化,針對復(fù)雜材料(多孔、復(fù)合材料等)、復(fù)雜本構(gòu)(應(yīng)變梯度、各向異性等)的空腔膨脹理論研究亟待開展。
(2)理想彈靶條件下空腔膨脹模型預(yù)測結(jié)果與實驗結(jié)果吻合較好,但在實際應(yīng)用中,彈靶條件更加惡劣,彈體著靶存在著角、攻角,靶體存在自由面效應(yīng)、側(cè)向約束、隨機骨料等,解決多層復(fù)合靶板、間隔靶板、彈體旋轉(zhuǎn)、彈體頭部刻槽等復(fù)雜情況下的空腔膨脹模型仍是一個巨大挑戰(zhàn);結(jié)合彈靶邊界條件,發(fā)展可描述復(fù)雜化作用條件空腔膨脹阻力模型和彈體侵徹動力學(xué)計算方法,是下一步工作的重點。
(3)絕大多數(shù)空腔膨脹理論研究工作將模型簡化為球/柱對稱。而隨著高超聲速武器、星載高速動能武器的發(fā)展,適應(yīng)于上述武器平臺的異構(gòu)型彈體的侵徹行為將成為熱點問題之一[73,105]。對于任意截面空腔膨脹問題,使用保角變換[106-107]、傅里葉變換[72]、最小二乘擬合等數(shù)學(xué)方法可以簡化橢圓積分、降低微分方程組的求解難度。如何結(jié)合異構(gòu)型彈體結(jié)構(gòu)特點及新的數(shù)學(xué)方法,發(fā)展可描述任意截面形狀的空腔膨脹模型,將是未來發(fā)展的重要方向之一。
(4)空腔膨脹理論早期應(yīng)用在剛體侵徹階段,后來擴展到高速和超高速階段。正如Rubin[24,52]、Rosenberg 等[22-23]指出,空腔膨脹理論的基礎(chǔ)假設(shè)具有局限性,存在穩(wěn)態(tài)流場與假設(shè)不一致、高速情況下無法預(yù)測“空化”現(xiàn)象等。研究者需要重新審視空腔膨脹理論假設(shè),著眼于求解思路、方法上的進(jìn)步,不局限在對材料本構(gòu)上的小修小補,擴大與增加模型的適用性與準(zhǔn)確度。

