球諧旋轉變換結合非全次Legendre方法的局部六邊形網格重力場球諧綜合

李新星, 李建成, 劉曉剛, 范昊鵬, 靳超

1 武漢大學測繪學院， 武漢 430079 2 信息工程大學地理空間信息學院， 鄭州 450001 3 西安測繪研究所， 西安 710054 4 61365部隊， 天津 300000

0 引言

傳統基于等角地理網格的地球重力場描述面臨著許多無法克服的局限性，包括網格面積不等、重力場平滑因子復雜、觀測數據冗余、積分離散化誤差大等，而六邊形的“離散球面網格系統”(Discrete Global Grid System,DGGS)因其良好的特性，在遙感、氣象、水文等領域取得了廣泛應用(Sahr et al.,2003). 作為地理網格的延伸，美國著名學者富勒(Fuller)最早進行了球面離散化的相關研究并且發明了“網格球頂”(Geodesic Dome)結構，之后許多學者關于球面網格系統的研究都直接或間接地受到了他的影響(張永生等,2007). 近年來，隨著DGGS網格系統不斷完善，其已經在諸如矢量數據結構(Dutton，1999)、空間數據索引(Dutton,1996a)、制圖綜合(Dutton,1996b)、全球動態數據結構(Goodchild and Shiren,1992)、全球土地監測(Suess et al.,2004)、全球海洋分析(Kidd et al.,2003)、全球氣候模型(Randall et al.,2002)、海洋路徑規劃、城市交通規劃(Brodsky,2018)等方面得到了應用.

基于六邊形的DGGS網格本應在重、磁場這一類具有各向同性特征的物理場中發揮更大作用，但是目前相關研究很少. 類六邊形網格結構在重磁場應用方面，Vestine等(1963a,1963b)較早研究了基于球面均勻分布點的地磁場的Poisson積分應用，Eicker(2008)將多種點位均勻分布方式引入到徑向基函數中進而求解衛星重力場取得了較好結果，Slobbe等(2012)將Fibonacci均勻分布引入球形斯列普基函數求解平均海水面和海面地形，Ran等(2018)將Fibonacci格網用于Mascon方法來反演冰蓋質量變化，以上均是在數值積分求解方面引入均勻分布結構，而鮮有在球諧分析與綜合中開展研究，其中最主要的原因在于，基于六邊形網格系統的點位并不像地理網格那樣是等緯度分布的，如圖1所示，從而需要大量締合Legendre函數(associated Legendre functions,ALFs)的求解，這對計算能力提出了更高要求(Pavlis,1988; 李新星等,2014; 田家磊等,2018).

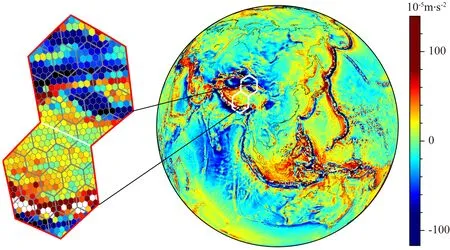
圖1 基于全球六邊形網格的360階全球重力異常分布圖Fig.1 360-degree gravity anomaly values based on global hexagonal grids

同時,觀測資料的精度與數量的增多使得對應球諧展開的階次也不斷升高,對計算能力同樣提出了挑戰. 例如目前有720階次的NGDC-720地殼磁異常模型(Maus,2010),有經典的2160階次地球重力場模型EGM2008(Pavlis et al.,2012),還有10800階次的地形、布格異常、均衡異常模型(Balmino et al.,2012; Hirt and Rexer,2015). 受限于球諧展開所需龐大的計算量,現有網格數據的分辨率已經遠遠走在現有模型階次對應分辨率的前列. 例如地磁場的磁異常網格數據EMAG2v3分辨率達到2′,根據Nyquest采樣定律,因磁場為偶極子場,其對應10800階次的球諧展開; sandwell和DTU15版本的海洋衛星測高重力異常分辨率達到1′(Sandwell and Smith,2008; Andersen and Knudsen,2016), 因重力場為標量場,所以其對應10800階次; GEBCO2014和GEBCO2019海底地形網格數據的分辨率分別達到了30″和15″,對應21600和43200階次; SRTM3、ARTER和ALOS全球DEM數據分辨率分別達到90 m、30 m和12 m,對應的球諧展開階次更高,因此,球諧展開中的嚴重耗時問題也是急需解決的.

針對ALFs及其相應積分、導數等函數的計算問題,許多學者從遞推方法、計算精度、計算效率和溢出問題等方面做了大量的工作. 對于ALFs的遞推方法,主要包括行推法、列推法、Belikov和跨階次遞推等四種方法,其中Belikov方法的計算效率最佳(李新星,2013). 為了解決遞推過程中的溢出問題,Fukushima (2012)提出了X數法實現了任意階次ALFs的遞推計算,代價是損失了一定的計算效率; Xing等(2020)改進了Belikov方法,解決了Belikov原遞推公式在高階次出現溢出的情況,例如緯度為75°的ALFs當階次達到4800時，ALFs的計算出現溢出; 張傳定等(2004)首次提出ALFs的跨階次遞推方法,并經驗證在20000階次以內其計算準確且不會發生溢出(于錦海等,2015).

關于ALFs遞推計算效率的進一步提升,目前還沒有較為顯著的方法. 學者大多繞過ALFs的計算,通過盡量減小ALFs的計算量來尋求提升球諧綜合(Spherical Harmonic Synthesis,SHS)和球諧分析(Spherical Harmonic Analysis,SHA)計算效率的方法,例如在SHS和SHA中要求相應的計算點等緯度網格分布,從而計算同一緯圈上所有點的模型值只需要計算一次該緯度的ALFs. Clenshaw(1957)提出Clenshaw求和方法避免大部分Legendre函數值的求解來提高SHS的計算效率,同時快速傅里葉變換(Fast Fourier Transform,FFT)技術的使用大大加速了球諧分析與綜合的計算,例如Colombo(1981)在球諧分析中使用了一維FFT,Sneeuw和Bun (1996)利用球面到輪胎面映射實現了二維FFT的球諧分析與綜合. 盡管FFT技術加快了SHS的計算速度,但其僅限于在計算規則網格分布下具有相同高度的點集,針對非等緯度、不同高度分布點的SHS和SHA,有學者采用了泰勒級數展開或等間隔內插的思想來提升效率(Kunis and Potts,2003; Moazezi et al.,2016; Seif et al.,2018).

實際應用中,更多是針對局部重力場或磁場數據的處理,為了解決因球諧方法計算量龐大而不便于局部使用的問題,學者們避開球諧模型,使用局部擬合、等效源、矩諧分析、球冠諧分析等方法來進行局部物理場的建模(徐文耀和朱崗昆,1984; 高金田等,2005; Younis,2013),而上述方法存在的邊界效應、基函數不正交、非整階Legendre遞推等問題還需要深入研究,如果球諧模型變得更加高效,也必然能夠在局部重磁場模型構建中發揮重要作用.

本文從ALFs求解方面入手,尋求提升其計算效率的方法. Jekeli等(2007)總結了不同緯度下ALFs函數值的量級隨階次升高的衰減關系,通過利用圖2a所示的逆向行推方法,求解ALFs值的有效部分,對于絕對值較小(例如<10-15)的值默認為0而不進行計算,從而節約了遞推過程中的計算量,在全球SHS過程中,該方法理論上能夠節約36%的計算量,但是由于其逆向行推方法計算效率偏低,并沒有給出最終的計算耗時比較.

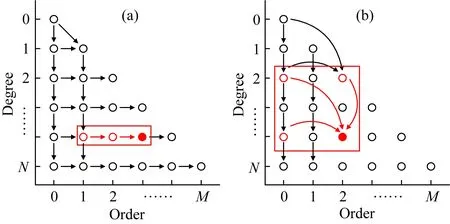
圖2 ALFs的逆向行推法(a)和跨階次遞推(b)方法Fig.2 The increasing order (a) and cross-degree-order (b) recursion formula for ALFs

本文利用該思想,結合跨階次遞推方法,提出了非全次Legendre(Non-full-order Legendre,NFOL)計算方法,實現了高緯度區域任意點的快速球諧綜合. NFOL方法是在利用跨階次遞推方法計算ALFs時,當遞推到達ALFs有效值(例如>10-15)邊界即可停止遞推,從而減小計算量,提升效率,由于有效值分布在全部“階”中“次”偏小的區域,所以該遞推只需要遞推全部階的部分“次”.

對于中低緯度的ALFs計算,由于ALFs有效值區域幾乎遍布整個階次,所以NFOL方法在低緯度區域并不適用,針對該問題,本文引入球諧旋轉變量變換(Spherical Harmonic Rotation,SHR)方法,該方法實現了坐標系旋轉下,對球諧展開系數的變換. 利用該方法將低緯度待求解區域的中心通過坐標系旋轉移至北極點,從而使得旋轉后的點位均位于“高緯度”,使得與之對應的ALFs有效值區域集中于低“次”部分,從而可采用NFOL方法提升SHS效率.

SHR方法在多領域具有重要作用. 地磁場模型中,該方法對于不同坐標系下磁場模型球諧系數間的比較、日變磁場Sq的內/外源場分離等具有重要作用(De Santis et al.,1996). 該方法求解過程中,Wigner D矩陣起到了重要的作用,許多學者研究了D矩陣及其遞推求解方法(Aubert,2013; Fukushima,2017).國內,許厚澤和蔣福珍(1964)較早研究了SHR原理并推導了公式,其在飛行器軌道擾動引力快速賦值中得到應用(任萱,1985; 鄭偉等,2011; 王建強等,2013),但是這些應用中采用的球諧系數階次較低,且其變換精度均沒有經過嚴格的精度評估. Fukushima (2017)利用X數法實現了2160階次球諧系數的90°旋轉.

本研究基于NFOL和SHR方法,分別實現了高緯度南極地區低分辨率的六邊形網格點重力異常、低緯度加里曼丹島地區的高分辨率六邊形網格點重力異常的構建,通過比較分析,驗證了方法的精度與效率,得到了有益結果,成果值得推廣.

1 非全次Legendre函數的遞推

1.1 球諧展開基本公式

對于球面上的平方可積函數,通過SHA能夠得到對應的球諧展開系數,這里以重力場中重力異常的球諧展開為例,其與重力場位系數之間的關系如下：

(1)

(2)

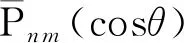
(3)

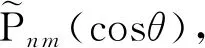
(4)

n≥2,n≠m

(5)

其中

(6)

遞推初始值為

(7)

當m≥2時,采用以下遞推公式(于錦海等,2015)：

(8)

其中

(9)

(10)

(11)

當m>2時,遞推系數cn m,dn m,hn m的值均小于1,因此跨階次遞推是穩定可靠的,遞推過程如圖2b所示.

1.2 非全次Legendre方法

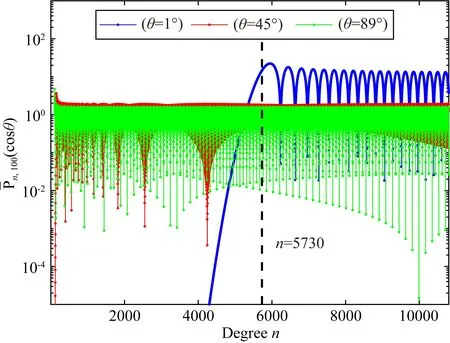
圖3 m=100時,θ=1°、45°和89°的ALFs的大小Fig.3 The value of ALFs with θ=1°,45° and 89° when m=100

m≈nsinθ.

(12)

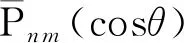
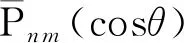
圖4 ALFs值中穩定振蕩區與快速衰減區的分界線,圖中綠色區域值較小,近似為0Fig.4 The boundary between the stable oscillation zone and the fast decay zone of the value of ALFs,the green area in the figure illustrates that the value is extremely small,approximately 0

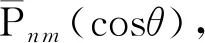
由于ALFs的值在該分界線周邊有一個衰減過程,如圖5所示,因此想要保證整個ALFs的計算精度,不能直接以式(12)所給出的直線作為分界線,而應該適當地向m增大和n減小的方向移動該直線,得到新的分界線

m≈nsinθ+t,

(13)

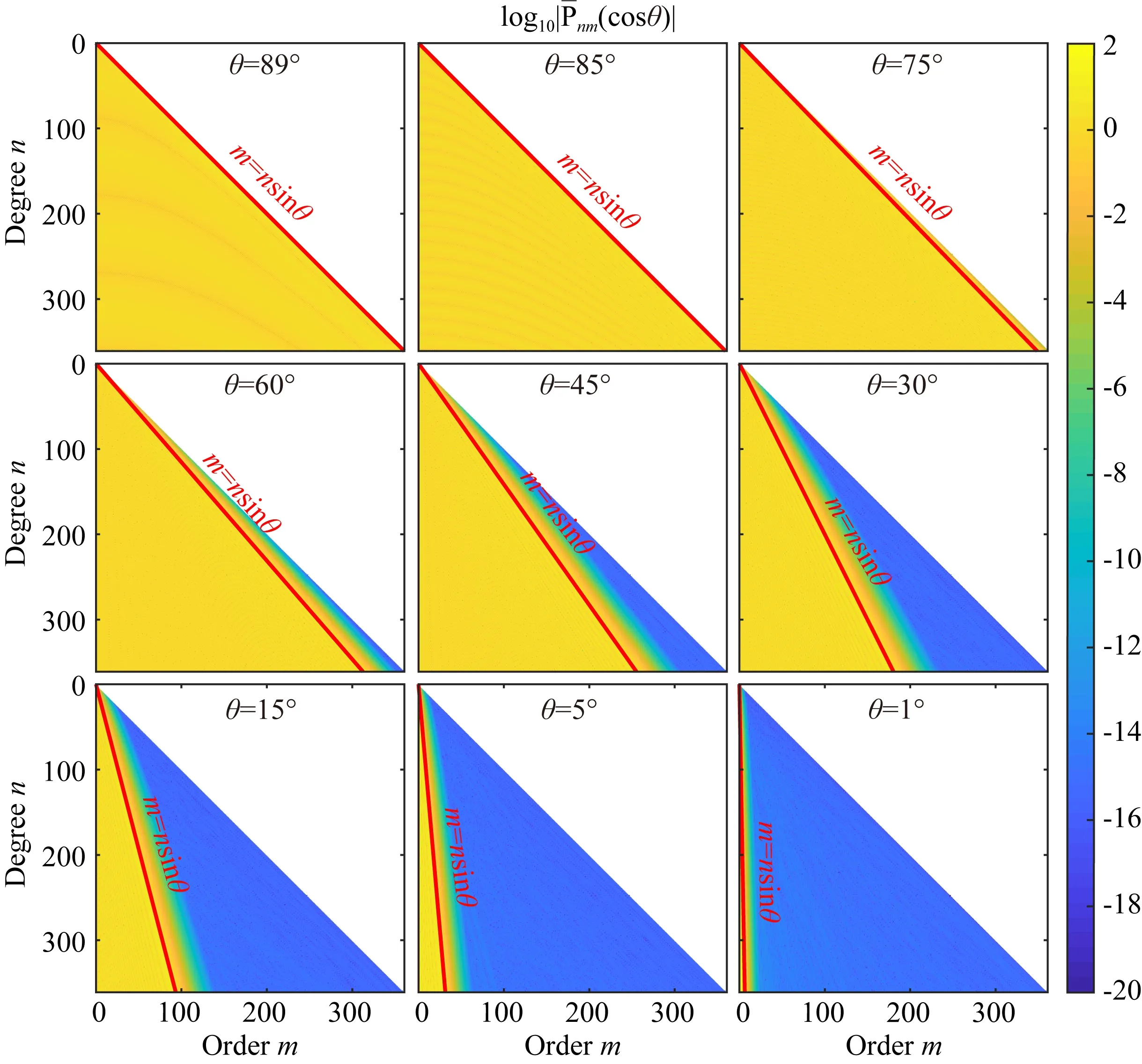
圖5 分界線周邊ALFs值的衰減過程,圖中藍色區域值小于10-20,可近似為0Fig.5 The decay process of the values of ALFs near the boundary,the blue area in the figure represents that the values are less than 10-20,approximately 0

其中參數t的大小決定了ALFs遞推值的精度和計算效率,t越大,精度越有保證,但ALFs需要遞推的區域會變大(見圖6),相應計算效率會降低,關于參數t的確定,會在后續實驗部分給出.

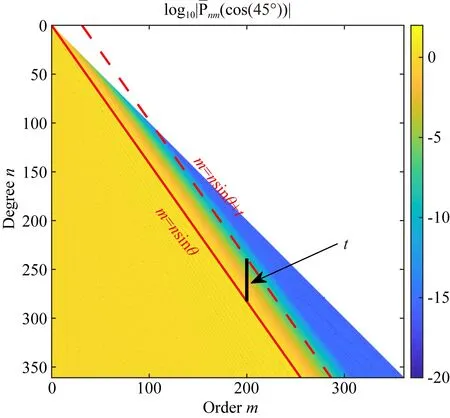
圖6 參數t的含義Fig.6 The meaning of parameter t

因此,上述方法確定了ALFs的遞推范圍,我們開創性地避開Jekeli等(2007)所采用的逆向行推方法,采用跨階次遞推方法計算了非全次遞推范圍內的ALFs值,解決了逆向行推不穩定且計算效率低下的問題.由圖5可知,對于非高緯度位置處的ALFs,顯然上述方法并不能有效提升計算效率,因此引入球諧系數的旋轉變量變換,通過換極將計算區域移至“高緯”區域,從而提升計算效率.

2 球諧旋轉變量變換(SHR)

2.1 沿z軸的旋轉變換

已知球面上一點Q(r,θ,λ),當坐標系O-xyz沿著z軸旋轉α角,記為Rz(α),得到新的坐標系O-x′y′z,則Q點在新坐標系下的球坐標為(r,θ,λ1),其中λ1=λ-α,即λ=λ1+α，如圖7所示.

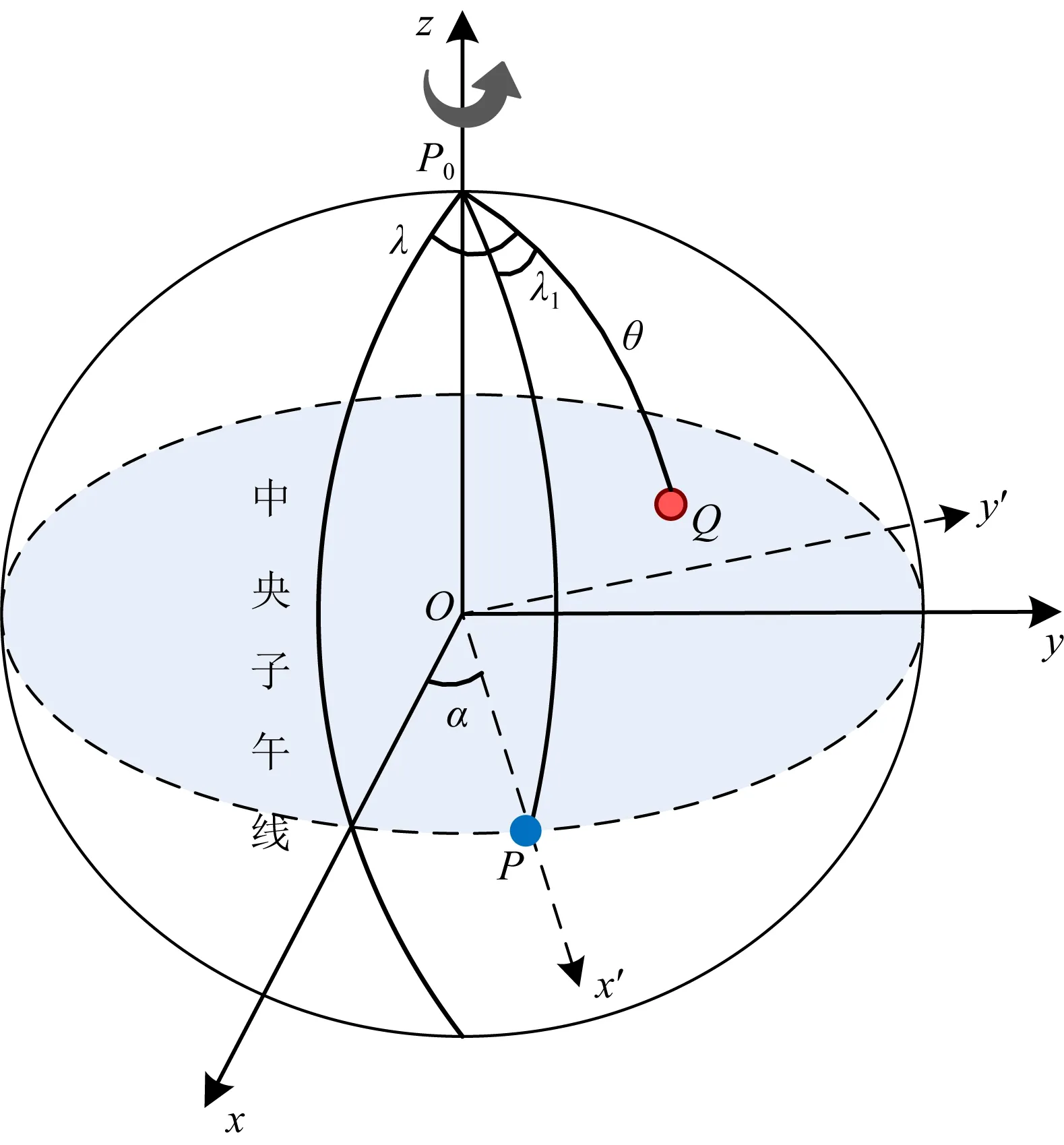
圖7 沿z軸的坐標系旋轉Fig.7 Rotation of the coordinate system along axis z

因此Q點的重力異常在新的球坐標系O-x′y′z下可展開為新的球諧系數

(14)

根據λ與λ1的以下三角關系式：

cosmλ=cosm(λ1+α)=cosmλ1cosmα

-sinmλ1sinmα，

sinmλ=sinm(λ1+α)=sinmλ1cosmα

+cosmλ1sinmα，

(15)

代入式(1)并與式(14)進行比較,可得兩個坐標系下球諧系數之間的關系

(16)

式(16)即為坐標系沿z軸旋轉α角時,對應的球諧系數的變換公式.

2.2 沿y軸的旋轉變換

已知球面上一點Q(r,θ,λ),當坐標系O-xyz沿著y軸旋轉β角,記為Ry(β),得到新的坐標系O-x″yz″.

如圖8,Q點在新坐標系下的球坐標為(r,Θ,Λ),其中Θ為新坐標系下的球心余緯,Λ為新坐標系下的球心經度,Λ1與Λ互補,Q點的重力異常在新的球坐標系O-x″yz″下可展開為新的球諧系數,表達式與式(1)類似，

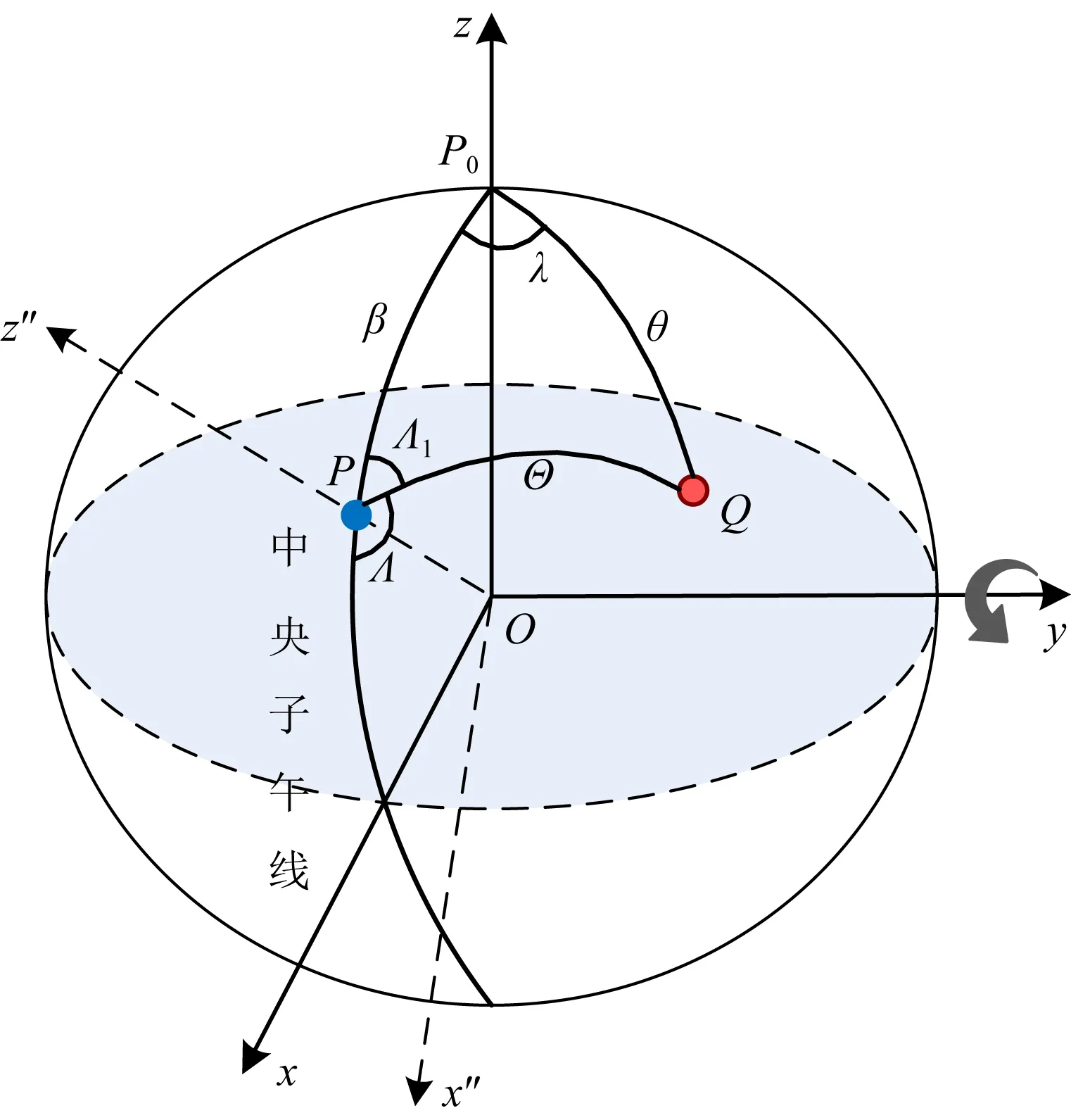
圖8 沿y軸的坐標系旋轉Fig.8 Rotation of the coordinate system along axis y

(17)

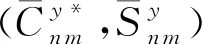
(18)

(19)

(20)

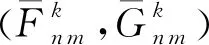
(21)

(22)

其中

(23)

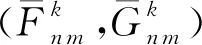
(24)

(25)

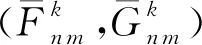
(26)

(26)式可利用D函數的對稱性及其與該兩組變量之間的對應關系得證,具體見Aubert(2013),即圖9d中k=4與圖9c中m=4對應的元素值相等.

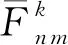
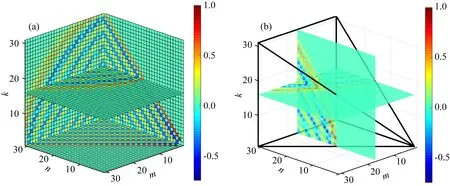
圖10 β=90°的30階值的切片圖(a) 30階球諧轉換矩陣的值; (b) 與比較說明式(29)對稱結構.Fig.10 Slice graph of the value of with β=90° and the n up to 30(a) Values of transformation matrix of in Eq.(29).

2.3 沿y軸90°的旋轉變換

(27)

其中

(28)

(29)

(30)

(31)

(32)

其中

(33)

(34)

(35)

上述遞推方法的計算過程中,Hn,m隨著n的增大快速減小,當其絕對值小于2.225×10-308的時候,數值發生溢出而強制為0,會影響后續遞推工作,因此在該遞推過程中應使用X-數法進行求解.

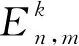
2.4 將(θ,λ)視為北極點的旋轉變換

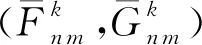
Zotter (2009)文中指出,Ry(θ)可分解為以下旋轉的組合：

Ry(θ)=Rz(π/2)Ry(π/2)Rz(θ)Ry(-π/2)Rz(-π/2)

(36)

還可以寫為

Ry(θ)=Rz(π/2)Ry(π/2)Rz(θ-π)Ry(π/2)Rz(π/2)

(37)

因此,只需要計算沿y軸旋轉90°的球諧系數變換以及簡單的z軸變換,就可以實現任意角度的旋轉變換,即

Ry(θ)Rz(λ)=Rz(π/2)Ry(π/2)Rz(θ-π)Ry(π/2)

×Rz(π/2)Rz(λ)，

(38)

其中系數的變換采用公式(16)和(18).

3 數值實驗及分析

為了驗證NFOL和SHR方法在局部六邊形網格重力場快速球諧綜合方面的應用,共進行三個實驗,計算環境如下：2.30GHz主頻的Intel Core i5-6200U CPU和8 GB主內存的PC機,64位Windows XP OS操作系統下VS2017編譯環境.

3.1 參數t的確定

第1節中指出,使用NFOL方法進行球諧綜合,需要確定公式(13)中的參數t,t取值越大,計算精度越高而對應效率越低,反之亦然. 因此,需要在滿足精度要求的情況下,合理的選擇t的大小來提高球諧綜合的計算效率.

利用2160階2159次的EGM2008模型位系數,計算地球表面點的模型重力異常值,利用不同緯度、不同t取值的NFOL方法計算重力異常,并與常規全階次方法計算的結果作為真值進行比較,結果統計見表1.

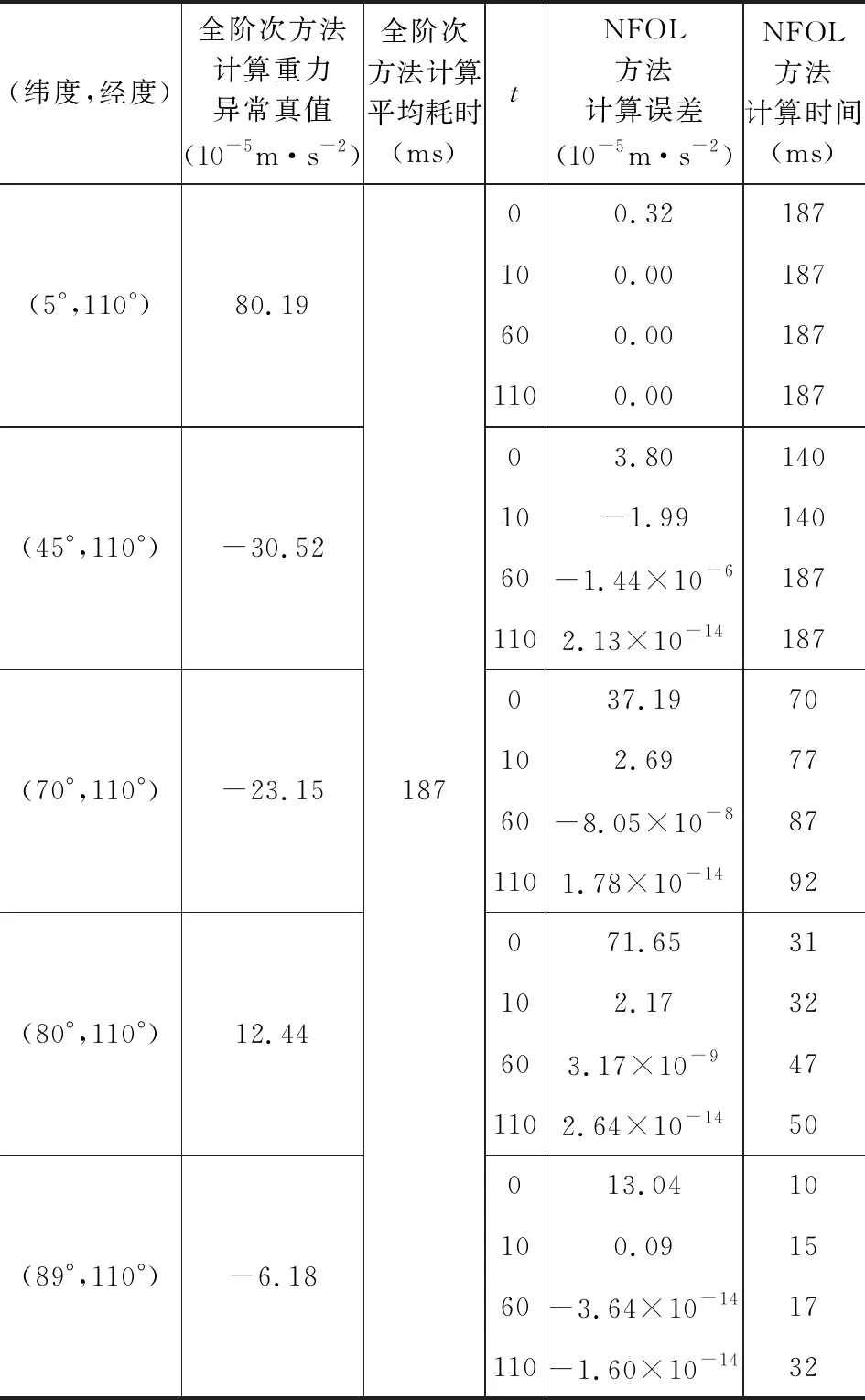
表1 不同緯度、不同t的2160階NFOL方法的球諧綜合結果統計

通過以上試驗,采用2160階次模型進行計算時,如果t取0,計算結果是錯誤的,說明t參數不能省略,取t=110可保證地面任意點位10-19m·s-2量級的計算精度,因此后續實驗采用t=110. 同時發現,當緯度低于45°的時候,利用NFOL方法并沒有明顯的優勢,緯度為60°～70°時利用NFOL方法效率提升近1倍.

3.2 南極地區(高緯度)六邊形網格重力場計算

本文基于張永生等(2007)所采用的基于二十面體的Synder等積投影(Synder,1992)及相應剖分方法生成ISEA4H(Icosahedral Snyder Equal Area aperture 4 Hexagon)網格系統,其中南極區域內包含17732個非等緯度分布的六邊形網格點,單個網格平均實地面積780 km2,網格平均間距約15.76 km. 這里利用2160階次EGM2008模型,采用全次和NFOL兩種方法計算網格點處的重力異常值,驗證NFOL方法在高緯度區域球諧綜合中的計算效能和精度,其計算結果和精度統計見表2和圖11、圖12.

表2 NFOL方法求解南極地區17732個點重力異常的性能統計(單位：10-5m·s-2)Table 2 Performance of the non-full order Legendre method for calculating 17732 point gravity anomalies in Antarctica (Unit: 10-5m·s-2)

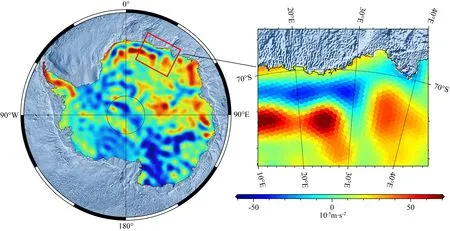
圖11 南極地區17732個六邊形網格點重力異常分布Fig.11 Distribution of gravity anomalies at 17732 hexagonal grid points in Antarctica

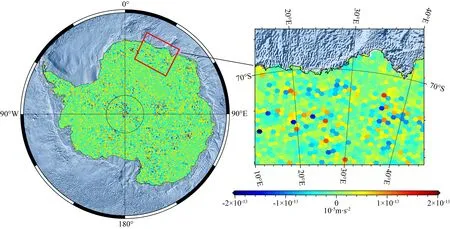
圖12 南極地區六邊形網格點重力異常NFOL解的精度Fig.12 Accuracy of gravity anomalies calculated by the non-full order Legendre method on hexagonal grids in Antarctica

由以上圖表可見,NFOL方法能夠保證平均10-19m·s-2量級精度水平的重力異常球諧綜合,計算耗時不到常規全階次求解耗時的一半,具有明顯的性能提升. 需要注意的是,當利用NFOL方法計算緯度小于45°的區域重力異常時,將失去其計算優勢. 為了將NFOL方法應用于中低緯度區域,我們結合SHR方法,構建位于赤道附近的加里曼丹島區域的六邊形高分辨率網格重力場.

3.3 加里曼丹島區域(低緯度)六邊形網格重力場計算

利用高分辨率的ISEA4H網格結構剖分加里曼丹主島區域,生成15125個非等緯度分布的六邊形網格點,單個網格平均實地面積48.75 km2,網格平均間距約3.94 km.

首先確定加里曼丹島區域中心的地心坐標(θ=89.141°,λ=114.2°),然后根據2.4節所述方法,將北極點旋轉至該中心點,利用2160階次EGM2008模型位系數,通過(38)式的旋轉變換,得到新的球諧系數EGM2008R,該轉換過程總耗時不足500 s,通常可根據計算區域的位置提前計算.在旋轉變換后的坐標系中,加里曼丹島的六邊形網格點均位于新北極點附近,故均屬于“高緯”,因此使用NFOL方法,以EGM2008R系數和旋轉后的坐標作為輸入,計算15125個點的重力異常值,并與利用EGM2008模型和旋轉前的坐標、基于常規全階次方法的計算結果進行比較,結果見表3以及圖13和圖14.

表3 SHR+NFOL方法求解加里曼丹島地區15125個點重力異常的性能統計(單位：10-5m·s-2)Table 3 Performance of the NFOL combined with SHR for calculating 15125 point gravity anomalies in the Kalimantan area (Unit: 10-5m·s-2)

圖13 加里曼丹島地區15125個六邊形網格點基于SHR+NFOL方法計算的重力異常結果Fig.13 The results of gravity anomalies calculated by the non-full order Legendre method combined with SHR at 15125 hexagonal grid points in Kalimantan Island area

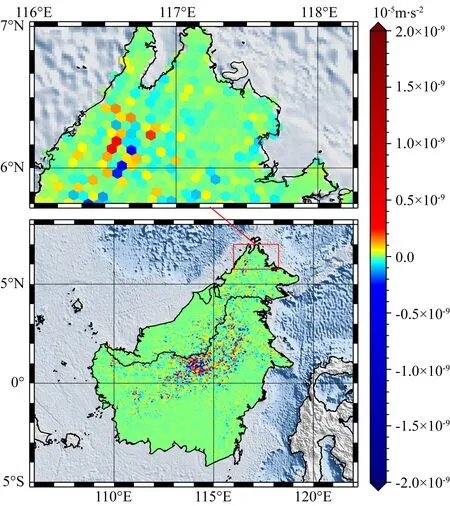
圖14 加里曼丹島地區15125個六邊形網格點基于SHR+NFOL方法計算重力異常的精度情況Fig.14 The accuracy of gravity anomalies calculated by the non-full order Legendre method combined with SHR at 15125 hexagonal grid points in Kalimantan Island area

本次計算的重力異常的精度水平為10-16m·s-2,比3.2節中直接使用NFOL方法求解精度水平10-19m·s-2低,說明SHR由于采用坐標變換和球諧系數的變換,引入了計算誤差,該誤差導致重力異常的計算誤差約10-16m·s-2; 同時可以發現,此次實驗中，NFOL方法計算效率是全階次解的近5倍,加速效果更加明顯,這說明,相比3.2節中的大區域、低分辨率六邊形網格點重力異常的球諧綜合,NFOL方法在小區域、高分辨率離散點的球諧綜合中更具優勢.

4 結論

為實現局部六邊形網格重力場元模型值的快速計算,以南極洲和加里曼丹島區域的六邊形網格點重力異常計算為例,研究了NFOL和SHR方法在球諧綜合快速計算中的應用.

首先,對ALFs遞推過程及其數值特征進行了詳細分析,給出了其值從穩定振蕩區到快速衰減區的分界線的理論表達式,利用分界線表達式對“次”進行有效截斷,聯合跨階次遞推,提出了基于NFOL方法的高緯度點快速球諧綜合. 在低緯度區域六邊形網格重力異常計算方面,首次將SHR與NFOL方法結合,通過坐標系旋轉,將低緯度區域的點變換到“高緯度”區域,從而利用NFOL方法實現低緯度區域的快速球諧綜合. 通過變量變換理論推導,借助X-數法,實現了2160階次球諧系數的任意角度旋轉下的變換.

通過數值實驗及分析,我們得到以下結論：對于2160階次的Legendre遞推,若保證全球任意點處計算重力異常的精度滿足10-19m·s-2,ALFs從穩定振蕩區到快速衰減區的分界線理論表達式中t的最佳取值為110; 在高緯度區域(≥60°),NFOL方法能夠平均提升ALFs求解和球諧綜合的效率近1倍,緯度越高,效率提升越明顯,最高可提速近10倍,且在雙精度數值運算中,能夠保證重力異常10-19m·s-2的平均精度水平,基于此構建了南極洲地區的六邊形網格重力異常; 在中低緯度區域(<60°),NFOL方法借助SHR,同樣能夠實現加速效果,其重力異常計算精度在10-16m·s-2水平,精度足夠滿足應用需求，且本文提出的SHR+NFOL方法在進行小區域高分辨率大量離散點的球諧綜合應用中具有明顯優勢.

需要強調說明,NFOL方法是對ALFs計算效率的提升,而對于非等緯度點球諧綜合的計算效率提升方法還有很多,例如采用Seif等(2018)提出的Legendre內插方法,能夠更快地實現六邊形網格重力異常的計算,而本文提出的NFOL方法與其他提升球諧綜合效率的方法并不沖突(FFT方法除外,因為其不需要計算ALFs),加速效果可疊加.

致謝感謝戰略支援部隊信息工程大學李姍姍教授對文章提出的指導性修改意見,賁進、童曉沖教授在生成六邊形網格方面給予的幫助和指導.