數學教學應從三個方面培育學生思維的深刻性

孔德宇

思維的深刻性是指思維活動的深度、廣度和難度，以及思維活動的抽象程度和邏輯水平。培育思維的深刻性對學生學習數學、形成數學思維具有至關重要的作用，也是落實學生核心素養的有效途徑。因此，一線教師應當將培育學生思維的深刻性滲透于日常教學活動中，讓數學教育為學生的終身發展奠定重要基礎。

一、重視概念教學，為思維深刻性的培育提供土壤

概念是數學的基石，數學思考的本質是建立在數學概念上的思考，學生對概念的理解直接影響到其對數學和數學方法的認識。因此，教師要讓學生在接觸每一個概念伊始，便感受到數學思考的魅力，使概念教學成為培育思維深刻性的土壤。筆者以蘇科版教材八年級下冊“11.2反比例函數的圖象與性質”一課為例，探索“反比例函數的圖象”這一概念生成過程中“由數想形”的方法，談談如何讓思維的深刻性在概念教學中得到發展。

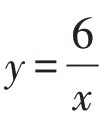
教學時教師要注重學生的體驗，讓學生參與到思考和解題的過程中，從而一步一步、有淺及深地明確概念的含義，培育學生思維的深刻性。本例中“由數想形”的過程能幫助學生理解函數表達式與函數圖象之間的對應關系，加深其對“數形結合”思想的理解。這就為學生后續研究新的函數的圖象及其特征提供了思路和參考，幫助學生建立起關于函數及其圖象的整體概念和解題思路。

二、重視構建知識網絡，為思維深刻性的發展提供信息支撐

數學中思維的深刻性就是運用數學概念、定理等，借助邏輯推理的方式，獲得接近問題本質的結論。在這個過程中，主體的知識結構影響著邏輯推理的深度。因此，要發展學生思維的深刻性，需要重視構建全面、系統的知識網絡，使學生在面對新的問題時能夠從已有的知識網絡中迅速提取與之相關的信息。下面，筆者以一道常見的數學題為例，談談知識網絡構建及其對發展思維深刻性的重要作用。

如圖1，已知一次函數y＝2x＋4的圖象過點A（1，6），并與y軸相交于點B。若將該一次函數圖象繞點A順時針旋轉45°得到直線CD，求直線CD的函數表達式。

（圖1）

考慮到旋轉角是45°的特殊性，教師可引導學生回顧三角形所學知識，構造等腰直角三角形來解決問題。在學生根據三角形性質得出本題答案后，教師可以進一步提問：若直線繞點A旋轉30°或60°，可以求出旋轉后的直線解析式嗎？引導學生沿著這一路徑思考，最終可以發現：若將直線繞直線上（或直線外）的確定一點（已知坐標）旋轉任意角度α（0°＜α＜180°），只需要知道這個角的某一三角函數值，便可求出旋轉后直線的解析式。通過分析歸納，使直線在平面直角坐標系中繞點旋轉的問題一般化，為學生今后的學習提供更高階、立體的知識網。

該環節中，教師引導學生從特定的例題中歸納出解題的一般方法和思路，將特定情境下的問題推廣到一般情境，體現了對學生的思維深刻性的培養。所以，教師在構建知識網時應注重知識辨析，強化知識網中知識點之間的橫縱聯系，培養學生的思維深刻性的同時，為其深度思考提供必要的信息庫。

三、選擇恰當素材，讓思維的深刻性自然生長

在實際教學中，為了達到某種特定的教學效果，教師常根據實際需要編制合適的練習。為培養學生思維的深刻性，在學生掌握勾股定理后，筆者編制如下問題：

如圖2，在網格圖中（每個小正方形的邊長為1個單位），線段AB經過平移運動到A'B'的位置，給出下列說法：

（圖2）

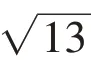
其中完全正確的有________。（填序號）

本題的本質是線段平移問題，常見的解題思路都是將圖形沿網格線平移，這就導致學生形成思維定勢，認為網格背景中的平移只能沿網格線進行。因此，筆者在學生學完勾股定理后設計了這一問題，將點移動的路徑設置為“網格中任意平移”，抓住與固有思維之間的矛盾，引起認知沖突，使學生認識到只要“確定一對對應點的平移方向與距離”即可完成題目。

其實教學中，教師還會遇到其他具體的問題，譬如針對幾何推理能力較弱的學生，可以選擇切入口寬、方法多、綜合性強的素材，引導學生對條件、結論進行深度分析；若學生對某一個或一類問題存在思維盲點時，可以選擇相近的有梯度的素材形成題組或小專題，促使學生打破思維定式，學會舉一反三。